基于正态分布衰减惯性权重的粒子群优化算法

徐浩天，季伟东，孙小晴，罗 强

哈尔滨师范大学计算机科学与信息工程学院，黑龙江哈尔滨 150025

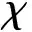
本研究使用改进参数设置方式，提出正态分布衰减惯性权重粒子群优化(normal distribution decay inertial weight particle swarm optimization, NDPSO)算法，针对惯性权重进行改进．NDPSO算法以正态分布曲线进行权重衰减，该正态分布曲线是一种非线性衰减曲线，早期衰减缓慢，中期衰减迅速，后期衰减趋于平缓，且权重衰减步数动态变化．该衰减策略充分利用了惯性权重可以提升传统PSO性能的作用．通过计算机仿真对比PSO、LDWPSO、EXPPSO、CFPSO、GDIWPSO、基于动态加速度系数的粒子群算法(particle swarm optimization based on dynamic acceleration coefficients, PSO-DAC)[18]和LUO[19]提出的惯性权重自适应粒子群算法(inertia weight adaptive particle swarm optimization, 本研究简称PSO-LH)以及NDPSO算法在8个标准测试函数中的收敛速度和收敛精度，证明NDPSO算法综合性能最佳．

1 粒子群优化算法及其改进算法

基本PSO算法中，速度和位移更新公式[1]为

vid(t+1)=ωvid(t)+c1r1[pbest(t)-xid(t)]+

c2r2[gbest(t)-xid(t)]

(1)

xid(t+1)=xid(t)+vid(t+1)

(2)

其中，vid(t+1)和xid(t+1)分别为粒子i在第t+1代的第d维速度和位置；c1和c2为学习率；r1和r2为[0, 1]间均匀分布的随机数; pbest(t)为粒子个体在第t代所得的最优位置信息； gbest(t)为种群在第t代所得的最优位置信息； 惯性权重ω计算式[12]为

(3)

其中，ωmax和ωmin分别为最大和最小加权系数；tmax为最大迭代次数．文献[12]的实验证明该参数能加快算法的收敛速度，且动态变化的ω比固定的ω效果更好，当ω从0.9动态衰减到0.4时性能最佳.

EXPPSO算法[13]中的ω与LDWPSO算法中的ω不同，ω被递减的指数函数e-αE替代，其中，αE为影响移动步长的大小，由当前迭代次数控制，则速度公式修改为

vid(t+1)=e-αEvid(t)+

c1r1[pbest(t)-xid(t)]+

c2r2[gbest(t)-xid(t)]

(4)

由于指数函数的特点，算法前期搜索步长较大，扩大了搜索区域，保证了前期的全局搜索能力．后期较小的步长减缓粒子更新速度，避免极值问题．YAN等[13]通过实验证明，指数衰减策略可以很快找到最优解．

受非线性指数权重衰减的启发，本研究提出的NDPSO算法将从线性衰减和非线性衰减两个角度进行研究．其中，ω是以正态分布曲线进行衰减．在前期一定次数的迭代过程中，ω始终保持较大的数值，使算法的全局搜索能力持续最大，令算法能快速收敛到最优解所在的区域内．中期ω迅速衰减，全局搜索能力慢慢减弱，局部搜索能力逐渐增强，并最终使得两种搜索能力保持动态平衡．后期ω减小到一定值后，算法不断迭代，令其局部搜索能力达到最强．可见，该算法充分利用了ω对PSO算法收敛速度和能力的影响，动态变化的ω引导算法避免陷入局部最优，并且保证了收敛的速度．

2 NDPSO算法

针对现有的惯性权重线性衰减PSO算法存在的衰减机制落后、速度较慢和易陷入局部最优等缺点，本研究引入正态分布曲线提出NDPSO算法，既保证了粒子群优化算法速度快的特性，还较好的克服了易陷入局部最优的缺点．

正态分布也叫常态分布，是连续随机变量概率分布的一种，在自然界和人类社会普遍存在．一般正态分布的函数公式为

(5)

其中，x为随机变量；μ为正态分布的位置参数，描述正态分布的集中趋势位置;θ描述了正态分布数据分布的离散程度.

为寻找合适的正态分布曲线，满足衰减机制，首先针对正态分布曲线的核心参数进行仿真分析．取θ=0.200 0～0.700 0， 由正态分布的算法机制可知，θ越大，图形越扁平，如图1．从图1可见，当θ=0.200 0时，曲线十分陡峭，随着θ增至0.400 0～0.500 0时，曲线基本满足NDPSO算法的要求．文献[11]通过大量实验证明，若ω以线性或非线性衰减，则0.9～0.4是较佳衰减值．本研究经大量仿真实验得到μ=0，θ=0.443 3为最佳值．故为使x=0时，f(x)=0.9， 设θ=0.443 3． 此时，正态分布曲线ω从0.9开始递减．将式(5)应用到标准PSO算法中，得到ω的非线性变化公式，如式(6)，速度更新则沿用式(1)．

(6)

其中，tmax为最大迭代次数；t为当前迭代次数；θ=0.443 3．

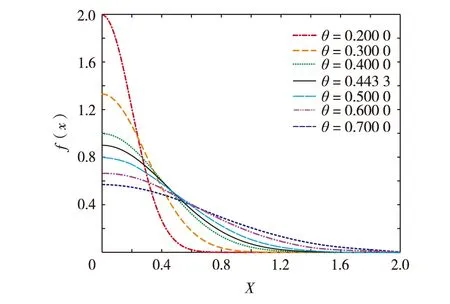
图1 正态分布曲线图Fig.1 (Color online) Normal distribution picture

为适应ω的变化特点，引入如式(7)的λ， 并采用式(8)为粒子群位置公式，使算法的搜索步长随着粒子的适应度值变化而动态变化．

(7)

xid(t+1)=xid(t)+λvid(t+1)

(8)

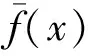
从图1可见，当x>0时，正态分布曲线呈“Z”型．在迭代刚开始时，由于初期整个解空间很大，为了加快收敛速度，ω保持0.9或比0.9略小的值，令算法以一个较大的步长搜索整个解空间，全局搜索能力此时达到最大，且收敛速度增加，也不易陷入局部最优．在经过一定的迭代次数后，ω开始迅速衰减，全局搜索能力逐步减弱；随着ω减小，搜索步长减小，算法达到全局搜索和局部搜索的平衡．当迭代将要结束时，ω的值已经极小，此时算法进入局部搜索，步长小，搜索不会遗漏最优解，由于后期能搜索的解空间已经相当小，所以收敛速度不会降低，这就令算法在保证速度的同时，能精确找到最优解．

1)初始化种群中粒子的位置和速度；

2)将粒子的pbest设置为当前个体最优值，将gbest设置为初始群体中全局最优；

3)计算每个粒子的适应度值；

4)对每个粒子，若粒子适应度值优于pbest，则更新pbest；

5)对每个粒子，若粒子适应度值优于gbest，则更新gbest；

6)根据当前迭代次数和式(6)计算ω的值，根据式(7)更新λ的值；

从《试点办法》的规定来看，值班律师参与认罪认罚案件始于侦查阶段。但是《试点办法》对值班律师的参与方式并没有明确的规定。《试点办法》仅仅在第10条中规定:人民检察院在审查起诉过程中应当听取值班律师的意见，犯罪嫌疑人签署具结书时值班律师具有在场权。这表明值班律师在认罪认罚案件中的参与程度还是有限的。

7)用式(1)和式(9)更新粒子的速度和位置；

8)判断算法终止准则是否满足，如果满足，算法停止；否则转向3)．

NDPSO算法的核心部分是ω的更新衰减策略，每次迭代都使用新的ω值来更新粒子的速度和位置．这样局部搜索能力和全局搜索能力在算法优化的每个阶段都能发挥应有的作用．这种 “Z”型曲线使算法不易陷入局部最优，且收敛速度很快．

3 仿真实验

通过对8个典型标准测试函数(表1，各函数具体表达式请扫描论文末页右下角二维码查看)的测试，比较NDPSO算法与其他改进PSO算法的性能．其中，f1到f4为单峰函数，f1(x)是一个简单的单峰二次函数，最小值为0，f3(x)的全局最小值位于抛物线形山谷中，很难找到最小值；f5(x)到f8(x)为多峰函数，f6(x)和f7(x)都具有多个局部最小值，很难找到最小值．对比算法分别为PSO、LDWPSO、 CFPSO、 EXPPSO、 PSO-DCA和PSO(LH)．

3.1 参数设置

PSO算法的参数有3种，ω、r1和r2、c1和c2． 其中，ω是控制当前速度对新产生速度的影响，用于平衡局部搜索和全局搜索能力；r1和r2是[0, 1]内的随机数；c1和c2为学习率，用来控制自身记忆和整个种群之间的相对影响．

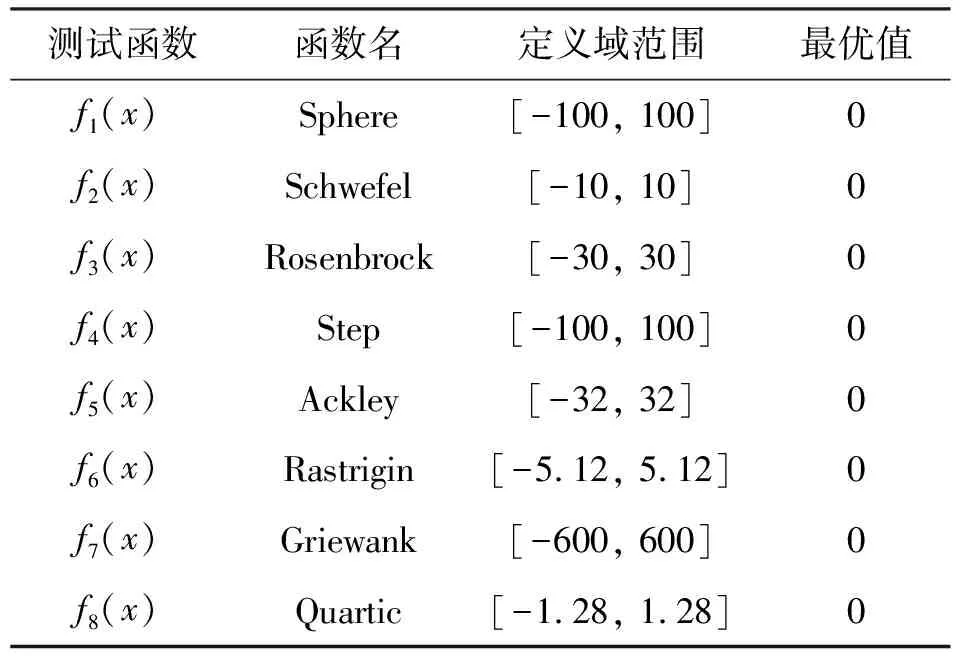
表1 八个标准测试函数

为保持实验的一致性，设置搜索维数为30，种群规模为30，最大迭代次数为1 000，c1=c2=2， π=3.141 59，ωmax=0.9，ωmin=0.4， 其余参数分别按照对应论文设置．每个算法计算20次，最优解取平均值．文献[12]指出，ω从0.9到0.4进行线性与非线性曲线衰减最佳，故为充分发挥正态分布曲线的优势，本研究设NDPSO的μ=0，θ=0.443 3．

3.2 仿真结果及比较

通过Matlab仿真，得到不同算法在8个测试函数中的收敛曲线如图2．8种算法的最优解如表2．其中，灰底数据为8个算法中精度最高的解．

函数f1(x)到f4(x)是简单的单峰测试函数，对比图2(a)至(d)和表2可见，NDPSO算法在保证收敛速度的同时，收敛精度也远大于其他改进PSO算法．由于f1(x)至f4(x)测试函数的单峰性，函数求解相对简单，EXPPSO和CFPSO算法的收敛速度可得到最大发挥，NDPSO算法的收敛速度次之．但是，EXPPSO和CFPSO算法是通过牺牲收敛精度换取速度，导致性能不如NDPSO和LDWPSO算法． 而且从图2(a)至(d)可见， 随着迭代次数的增加，NDPSO算法的收敛曲线下降明显，收敛速度和步长随着迭代次数动态调整，保证了算法在加快收敛速度的同时仍能保持最优解的精度．LDWPSO算法的收敛精度虽略次于NDPSO算法，但收敛速度大不如NDPSO算法．与NDPSO算法机理相似的GDIWPSO算法，虽然较其他算法有兼顾速度和精度的优势，但NDPSO算法综合效果更优． PSO-DAC和PSO(LH)算法无论是收敛速度还是收敛精度都远逊于NDPSO算法，这两种算法的惯性权重机制都未能发挥ω的作用．在单峰函数求解上，NDPSO算法能同时满足收敛速度和收敛精度要求．

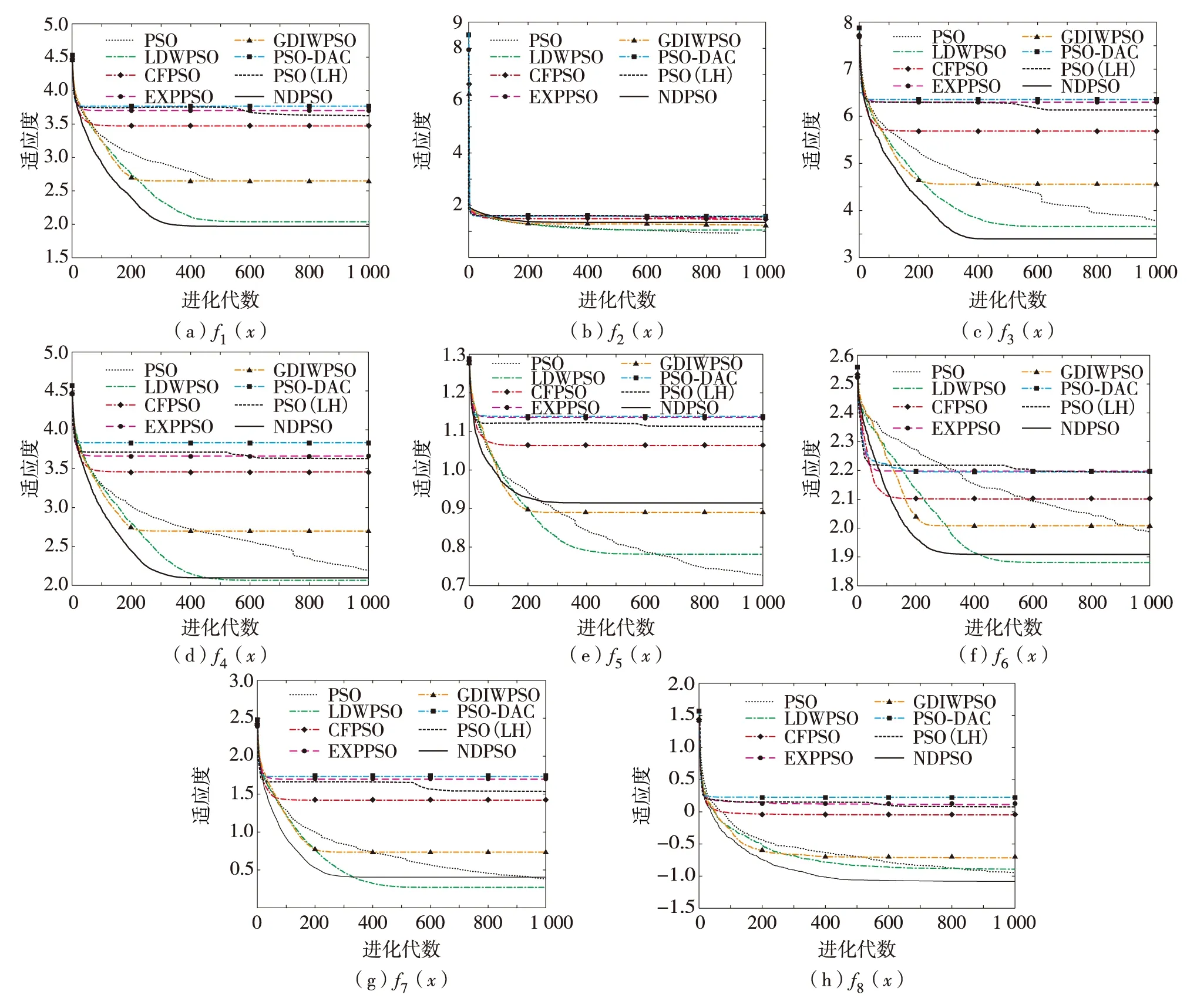
图2 不同算法在8个测试函数中的收敛曲线图Fig.2 (Color online) Convergence curves of different algorithms in eight test functions

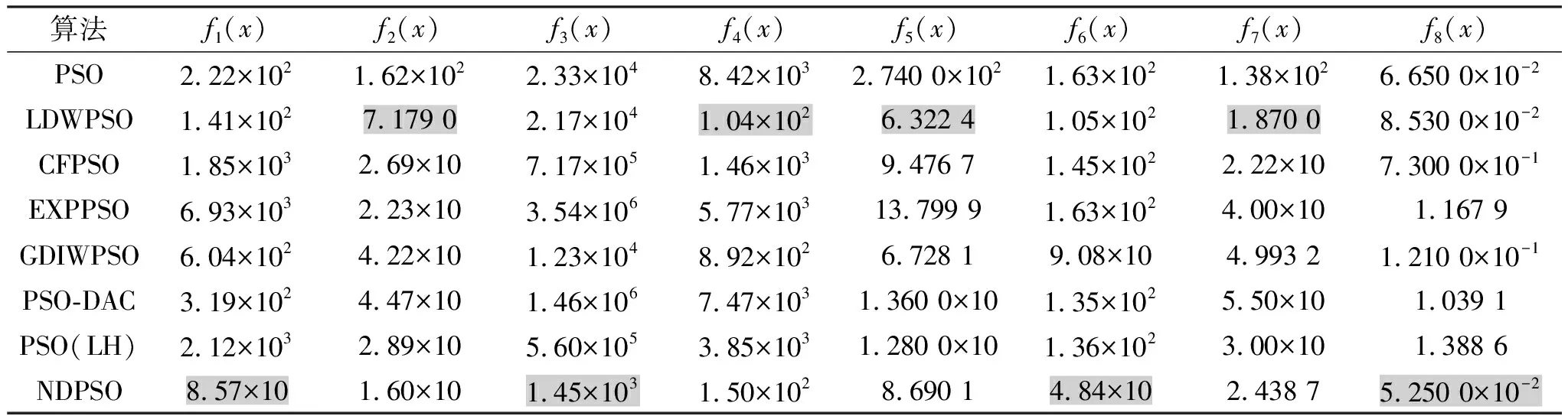
表2 不同算法在8个测试函数中的平均最优解1)

1)带阴影的数据为8个算法中精度最高的解

函数f5(x)到f8(x)是较为复杂的多峰函数，算法很容易陷入局部最优，导致无法收敛．结合图2(e)至(h)和表2发现，NDPSO算法在多峰函数上性能依然出色．在收敛速度上，NDPSO算法的表现比其他改进的PSO算法更好，且收敛精度也大幅提高．从图2(f)和(h)可见，NDPSO算法收敛速度最快且找到的最优解精度最高．与之相比，线性权重衰减策略的衰减机制在复杂的多峰函数只能保证收敛精度，不能保证快速收敛．由于多峰函数的特殊性，求解较为复杂，极易陷入局部最优．而NDPSO算法几乎不会陷入局部最优，其ω衰减机制保证了前期的收敛步长，防止陷入局部最优导致算法无法进行．

综上可见，NDPSO算法不管在单峰函数问题还是多峰函数问题上，总体性能都优于PSO、LDWPSO、CFPSO、 EXPPSO、GDIWPSO、PSO-DAC和PSO(LH)算法．

结 语

本研究利用正态分布的曲线特征，提出了一种基于正态分布衰减惯性权重的粒子群算法NDPSO．该算法前期缓慢收敛，中期加速收敛，后期趋于平缓，保证了算法在前期的全局搜索能力，中期局部搜索能力与全局搜索能力的平衡，后期强化了局部搜索能力．理论分析和实验数据比较发现，其他线性衰减权重PSO、收缩因子PSO和高斯分布PSO相比，NDPSO算法在简单的单峰函数测试中有着不俗的收敛速度和收敛精度，而在多峰函数测试中也始终能收敛到最优解和保持较快的收敛速度，说明NDPSO充分利用了ω对PSO算法收敛机制的影响，能解决多种优化问题．