旅游城镇路网多目标优化模型及算法设计

奚宽响，查伟雄, 2，李 剑, 2，严利鑫

1)华东交通大学交通运输与物流学院，江西南昌 330013；2)华东交通大学交通运输与经济研究所，江西南昌 330013

近年来，随着旅游热的兴起以及自驾游人数的增长，旅游城镇交通量增势迅猛，交通资源和交通需求之间的矛盾日益突出，旅游城镇交通拥堵已成为一个亟待解决的问题．目前对交通拥堵问题的研究主要集中在普通城市的交通拥堵管理政策和道路网络优化等方面．陈兆盟等[1]提出为缓解交通拥堵,允许私家车以收费模式驶入公交专用车道，建立基于拥挤收费的交通信号控制模型；史峰等[2]建立了交通微循环网络设计双层优化模型以缓解城市交通拥堵问题；张振东等[3]研究路票交易约束下的出行人通勤路径选择特性,基于可交易电子路票的运行机理,根据出行者效用最大化原理,构建通勤出行路径选择模型；KAROONSOONTAWONG等[4]建立基于通行能力的一般双层规划城市网络优化模型；张孜等[5]提出整数线性规划和双层规划模型,通过可变车道最大限度地提高路网的通行能力；秦进等[6]考虑网络结构、交通需求、出行选择及出行成本等因素,对既有定量化交通网络效率评价方法进行比较；王正武等[7]进行级联失效影响源重要度辨识和排序方法研究,为道路交通网络级联失效行为的管理与控制提供参考．

交通拥堵问题的研究在交通拥堵管理策略和道路网络优化及城市交通路网评价等方面已取得丰富成果，却鲜有针对旅游城镇交通拥堵问题的研究，旅游客流的持续增长使旅游城镇交通拥堵问题逐渐凸显．本研究基于旅游城镇的交通流特点及交通资源现状，从如何设计旅游城镇路网优化方案，使路网的各条路段饱和度适中且均衡、以及投资成本最低方面，探讨旅游城镇交通拥堵治理问题．

1 旅游城镇路网多目标优化模型

1.1 问题描述

旅游城镇道路交通资源的主要服务对象为外来旅游交通量，其出行目的单一，起讫点(origin-destination, OD)固定，出行路径具有很强的规律性．旅游城镇路网优化问题实际是基于旅游城镇路网现状，结合旅游城镇交通流特点，寻求最佳的路网优化方案，使旅游城镇的交通需求与交通供给达到平衡状态．

在旅游城镇路网优化问题中，设旅游城镇路网为G=(E,A)， 其中，E为网络节点的集合；A为网络节点间路段ai的集合．qi为第i条路段的交通量，将旅游城镇入口处定义为交通流起点，旅游城镇景点定义为交通流终点， 路段集合A就构成了OD之间的路网；xi为决策变量，表示路网中第i条路段新增车道数；若路网中共有N条路段且所有路段新增车道数的最大值均为M， 则路网共有(M+1)N种路网优化方案．旅游城镇路网优化问题即在投资成本最低、饱和度最适中且均衡的双目标条件下，求解所有路网优化方案中的最佳方案．

1.2 模型建立

旅游城镇路网优化要考虑旅游城镇的发展目标、交通流特点及道路优化条件等因素．在一定投入费用范围内实现路网交通拥堵治理与投入费用的最优平衡关系，为路网优化决策提供参考[8]．

饱和度是反映道路交通状况的重要指标，也是评判道路服务水平的重要基准[9]．根据文献[10]，饱和度小于0.5会造成道路资源浪费；饱和度大于0.8会造成路网交通拥堵．基于此，设置惩罚系数δi对不同范围的饱和度si给予不同惩罚，δi设定见表1．为尽可能保证si在0.5～0.8的合理范围，δi应满足δ5=δ1>δ4=δ2>δ3．

表1 不同范围饱和度下的惩罚系数设定

投资成本最低目标是从路网系统优化的角度，确定各路段的优化方案，从而使路网整体效益最优．本研究以各路段扩建车道所需的建设费用总和作为投资成本，构建目标函数

(1)

其中， minZ1为投资成本最小值；N为路网中路段总数；li为第i条路段的有效长度；xi为第i条路段新增车道数；σ为每车道单位长度建设所需的费用(单位：1个货币单位)．

饱和度系统最优目标是在路网整体饱和度均衡的前提下，确定最佳路网优化方案，降低路网整体饱和度，实现路网通畅的目标．为使路网整体饱和度趋于均衡，本研究以惩罚后的各路段饱和度总和最小为目标构建目标函数

(2)

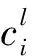
为投资成本最低和饱和度系统最优目标设定不同权重，可将该多目标优化问题转化为单目标非线性优化问题．建立模型为

minZ=λ1minZ1+λ2minZ2

(3)

s.t.

(4)

其中，λ1和λ2分别为投资成本最低目标和饱和度系统最优目标的权重；Z1为投资成本；Z2为路网整体饱和度；约束条件0≤Z1≤Z1max保证投资成本不应超出规划部门的投资预算，Z1max为投资预算值；约束条件Z2min≤Z2≤Z2max保证路网整体饱和度在合理范围内，Z2min和Z2max分别为路网整体饱和度下界和上界值．

本模型从(M+1)N种路网优化方案中筛选满足投资成本最低目标与饱和度系统最优目标的最佳方案．引入饱和度惩罚系数δi[12]， 将饱和度惩罚转化为货币支出，将δi作为经济惩罚，进而统一饱和度系统最优和建设费用最低两个目标的量纲．通过多次实验不断调整δi的值，使两目标的优化结果处于同一数量级，以消除两目标由于数值大小差异对优化结果产生的影响．

2 基于遗传算法的模型算法设计及目标函数权重分析

2.1 基于遗传算法的模型算法设计

上述优化模型为非线性优化模型，采用遗传算法求解，算法步骤如下：

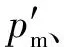
步骤2模型的决策变量为整数，故采用实数编码，利用随机函数与取整函数生成初始种群，随机生成psize个|nver|维向量．

步骤3将式(3)作为适应度函数，对产生的种群计算个体适应度值．

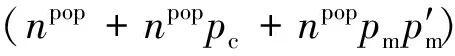
步骤5将前npop个个体复制1次得到2npop个新个体，采用联赛选择方法从群体中任意选择一定数目的个体，将适应度最高的个体保存到下一代．反复执行这一过程，直至保存到下一代的个体数达到npop为止，联赛规模Tsize=3， 按交叉概率对随机配对个体进行交叉操作，交叉npoppc次得到npoppc个新个体．

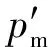
步骤7判断是否达到迭代总数，若否，则转向步骤3；否则，计算个体适应度值，对所有个体按升序排列选择操作，输出最佳个体npop(1)．

2.2 目标函数权重分析

λ1和λ2的取值不同将直接影响路网优化方案的选取．本研究选取不同权重取值进行算法实验，通过分析实验结果，筛选出最佳目标函数权重取值，筛选步骤如下：

步骤1按照λ1+λ2=1等比例将λ1及λ2分为K组值．

步骤2基于TransCAD平台，利用用户均衡模型将路网OD交通量分配到初始路网中，产生各路段初始交通量．

步骤3将路网具体数据与步骤2结果带入路网优化模型，利用Matlab软件按照上述遗传算法步骤实验K次，计算出λ1和λ2在不同取值下的最优解，得出不同的路网优化方案．

步骤4比较分析不同路网优化方案下，投资成本及路网中各路段饱和度的变化，筛选出路网中各路段饱和度适中且均衡、投资成本合理的最佳方案，确定λ1和λ2的取值．

3 算 例

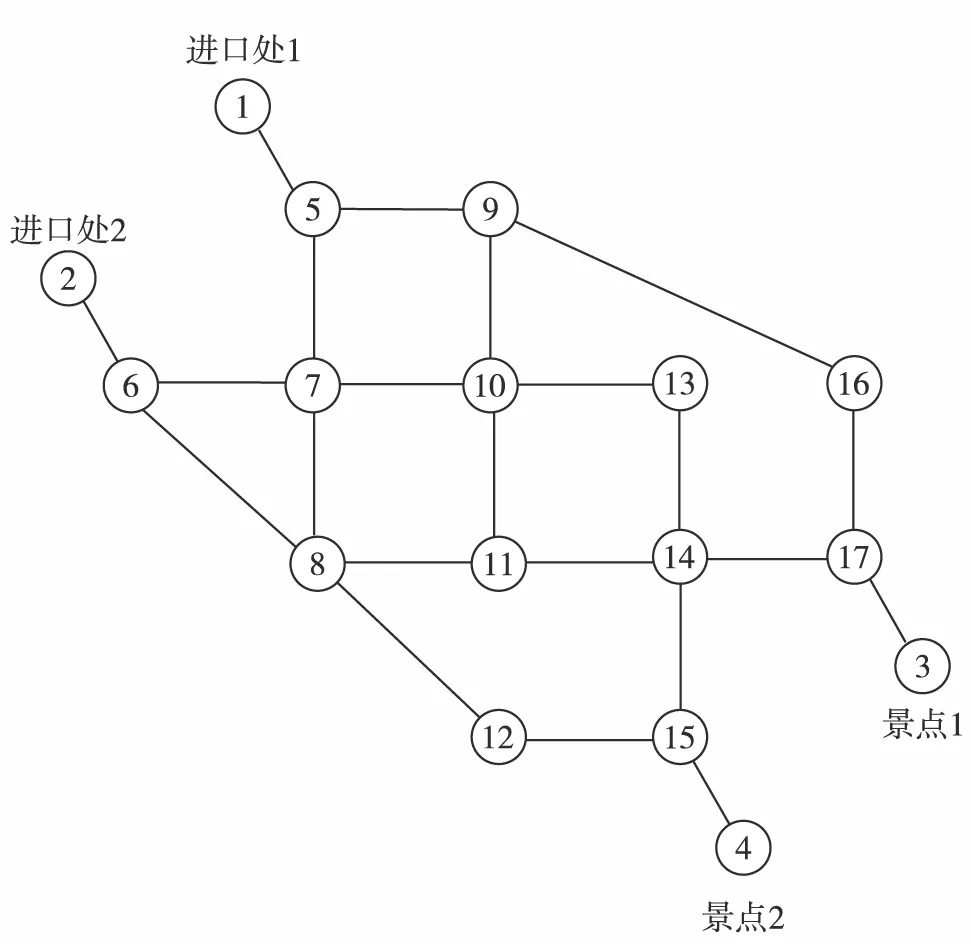
图1 某新型旅游城镇现状路网示意图Fig.1 The current road network of a new tourist town

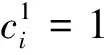
表2 某新型旅游城镇OD交通量

Table 2 OD traffic of a new tourist townpcu·h-1

基于以上算例的路网具体数据，通过用户均衡模型对初始路网进行流量分配，在TransCAD平台得出分配结果如图2．

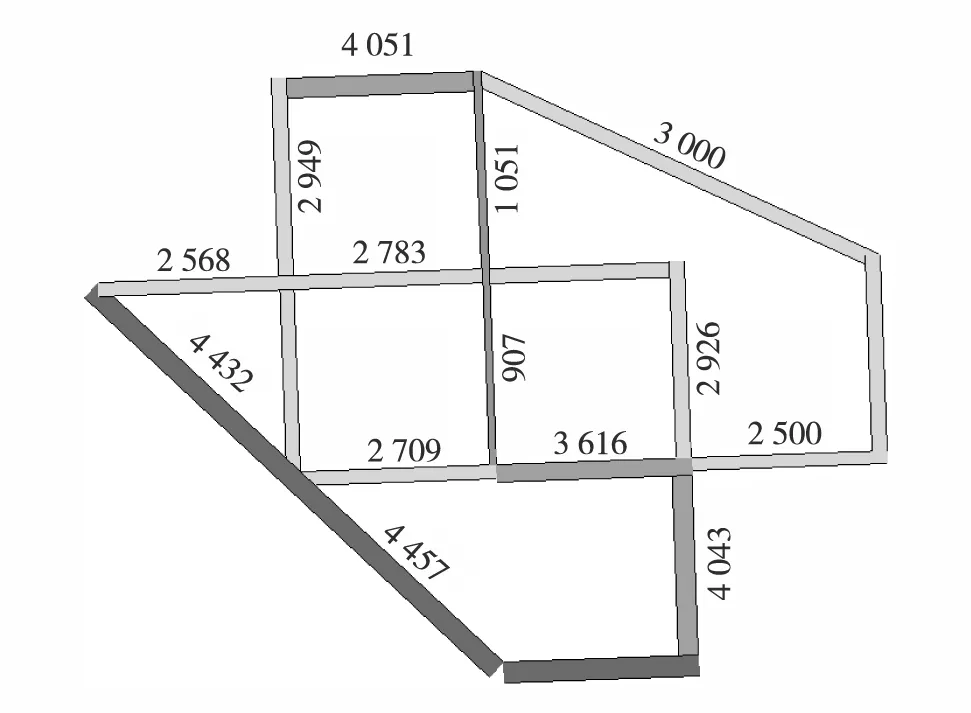
图2 某新型旅游城镇各路段流量分配示意图(单位：pcu·h-1)Fig.2 Flow assignment of each road section in a new tourist town(unit：pcu·h-1)

本研究参考文献[12]，通过多次算法实验不断调整惩罚系数的取值，得出不同优化方案，分析对比最佳方案确定惩罚系数的取值为δ1=10、δ2=1、δ3=0.5、δ4=1及δ5=10(单位：1个货币单位)．

算法实验过程中，在约束条件λ1+λ2=1下，通过不断在[0,1]内缩小相邻两组权重的均分间隔，发现当均分间隔为0.1后，实验结果的种类将不再增加，此时，[0,1]被划分为11组值，因此，选取K=11． 算法实验结果表明，当目标函数权重设定为λ1=0.2、λ2=0.8或λ1=0.1、λ2=0.9时，算例结果最合理，本例取λ1=0.2、λ2=0.8．

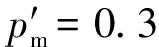
图3为遗传算法迭代收敛图．可见，当程序运行到第8代时，目标函数值开始逐渐收敛于最优解，当程序运行到第16代时，达到适应度函数的理论最小值51.899 3，此时xi的取值即为最优解，得到路网最佳优化方案如表3．对原有路网按上述方案优化后，可得路网中各路段饱和度的变化情况．路网各路段现状饱和度与优化后饱和度如图4．

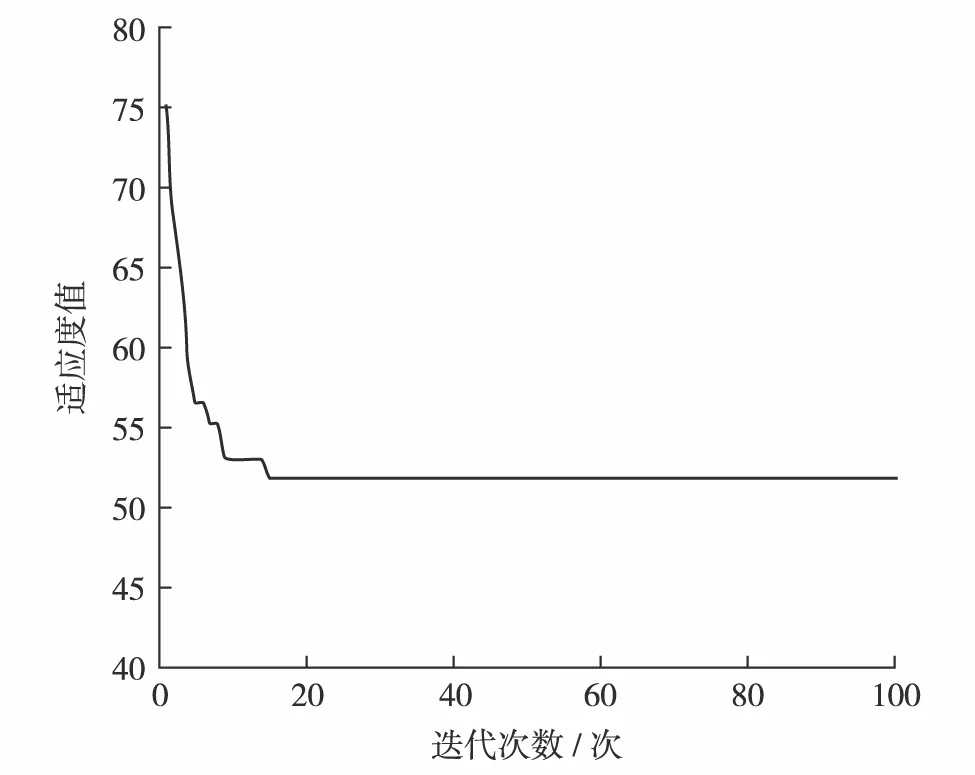
图3 遗传算法迭代结果Fig.3 Results of genetic algorithm

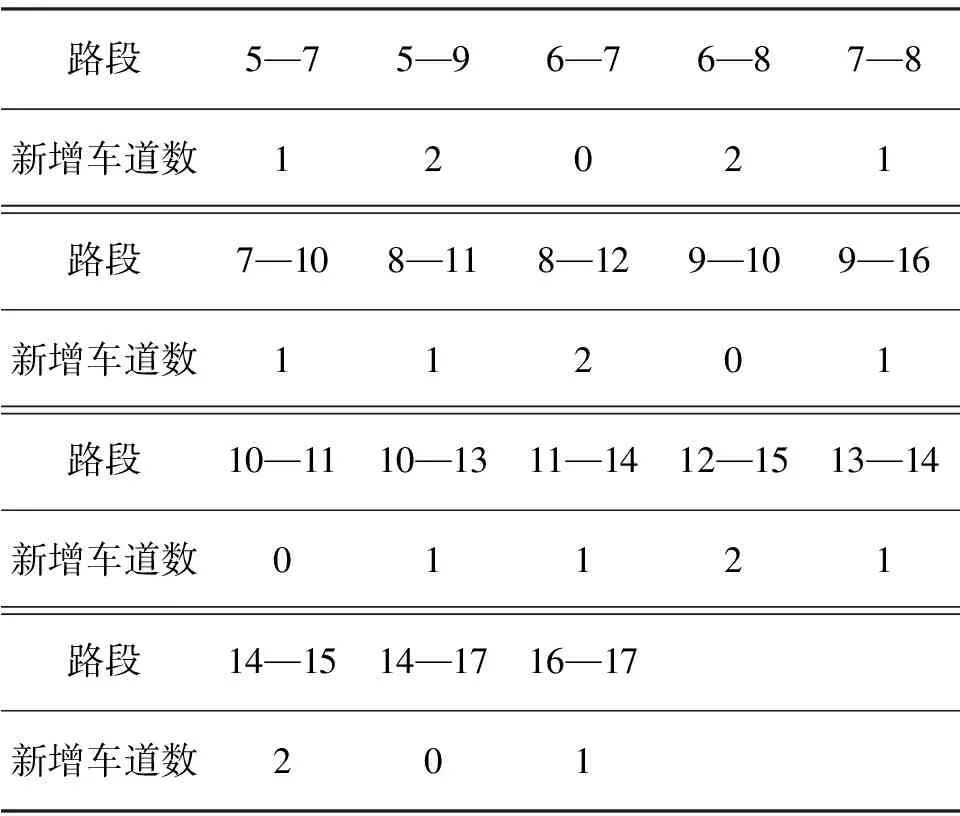
表3 各路段新增车道数

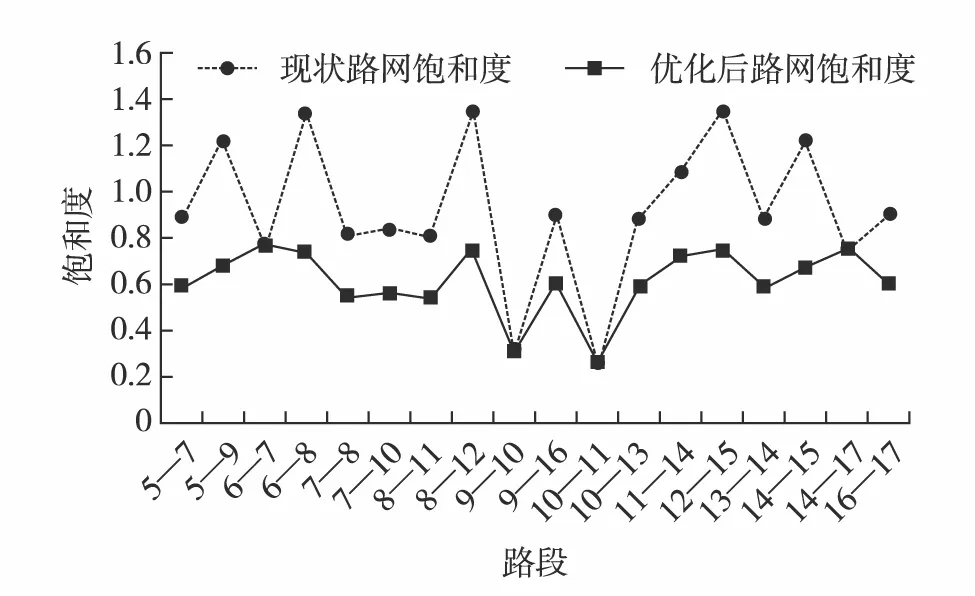
图4 路网优化前后饱和度对比分析Fig.4 Comparison of saturation between before and after optimization of road network

由图4计算可知，路网中所有路段饱和度的总和由16.70下降至11.12，路网中所有路段饱和度的平均值由0.93下降至0.62，说明整体路网的交通状况得到极大改善；路网中所有路段饱和度之间的标准差由0.31下降至0.14，说明路网中各路段的饱和度更为均衡．由图4可见，所有扩建车道的路段饱和度均介于0.5～0.8的饱和度合理范围内，说明模型的优化方法并未因投资成本过高、路段扩建车道过多而造成道路资源浪费，也没有因为投资成本过低使路段扩建车道数量不足而造成交通拥挤现象．

结 语

本研究针对旅游城镇交通流特性建立路网多目标优化模型，并综合考虑路网通畅程度和投资成本，结果可为旅游城镇的路网优化决策提供参考；在模型求解过程中，借助TransCAD平台，采用用户均衡模型进行交通量分配，使模型具有较强的工程实用性；通过多次算法实验分析确定目标函数的最佳权重，使路网通畅程度与投资成本达到最优平衡．最后，通过算例验证了模型的有效性．本模型尚未考虑路网优化后各路段交通量的变化，路网饱和度惩罚系数的设定方法也有待改善，这将是接下来的研究重点．