装配残余应力对管路影响规律的实验研究

徐 朔，贾世宇，张辽远

(沈阳理工大学 机械工程学院，沈阳 110159)

近年来，国内航空发动机管路系统在外场服役时，由于受卡箍的制造缺陷及卡箍连接的导管同心度超差等原因的影响，发动机管路系统中的卡箍、焊接点等位置受到了装配产生的残余应力的影响。这种残余应力的存在作用在管路上，使动载荷产生的应力与残余应力叠加后，应力幅值产生变化，对结构抗疲劳强度产生影响。残余应力既影响构件抵抗静、动载荷的变形能力，又影响载荷卸除后变形的恢复能力[1]。而航天发动机管路的工作环境是一个循环应力场的环境，若是管路系统中存在大量残余应力，会使得发动机内应力增大，影响发动机的稳定性，也会大大降低管路寿命及管路性能，造成管路提前失效、能源的大量损耗甚至出现事故。

航空管路的失效原因中，振动是主要的诱导因素，而随机振动疲劳又是一个主要的因素。在航空工程实际应用中，随机振动疲劳通常都是在疲劳载荷谱的作用下及预载荷所形成的准静态应力的基础上，同时叠加随机振动应力后所引起的疲劳破坏。预载荷会随着外力的增加而增加，没有自限性。当管路内塑性变形达到极限状态，即使外力载荷不再增加，管路仍将产生不可限制的塑性流动，直至破坏[2]。管路管材制作过程中的残余应力可采用时效的形式消除，但在管路系统的安装过程中由于装配产生的残余应力实时产生，且这种残余应力往往很大，会直接影响管路结构的使用寿命。因此，研究管路结构由于装配产生的残余应力及残余应力对管路结构的影响规律十分必要。现阶段对于发动机管路的固定连接方式与位置的确定，大多依靠的是设计人员参考原有的搭建模式或以经验设计，专门针对管路系统装配残余应力的研究极少。

本文使用动态信号测试分析系统对管路系统进行应力大小实时检测，研究装配节点距离对管路系统装配残余应力大小的影响；通过改变装配节点距离、管路长度及管内流量大小，研究分析装配节点距离对装配残余应力大小的影响规律。

1 理论分析

1.1 数学模型

将14阶流固耦合方程进行拉氏变换并整理，此方程便可用矩阵形式简化表示为

(1)

其中：

式中：Vf为流体流速；P为流体压力；VP为管道振动速度；F为管道内力；ω为管道转角速度；M为管道所受力矩；TA为14阶流固耦合方程拉氏变换后的系数矩阵；t为时间；f表示流体；式中各变量上标为坐标轴方向。

式(1)的通解为

X=AeλlzA-1X0

(2)

式中：x0为初始条件；λ为矩阵T的特征值；A为λ对应特征向量所组成的矩阵；lz为Z方向管长；e为自然常数。

根据式(1)、式(2)，同理可推导出小曲率弯管的模型公式，而大曲率弯管(弯管处曲率半径与管道比值大于3)可分解看作多个小曲率弯管的组合，即可得出弯管模型。将直管模型与弯管模型进行组合，便可得出各种形态下的二维管路模型公式，同理可推出三维管路模型计算公式。

1.2 残余应力检测机理简介

从20世纪30年代至今，已经发展出多种残余应力的检测方法，大体上可分为两类，即机械释放测量法和物理测量法；按对被测件的损坏情况，又可分为有损测试和无损测试两种。

刘金娜等[4]研究了材料残余应力测定方法的发展趋势，并归纳总结对比，如表1所示。

表1 残余应力测试方法比对表

其中，以X射线法与盲孔法发展较成熟，尤其是盲孔法。盲孔法是目前工程上最为常用的检测方法，美国ASTM(American Society for Testing and Materials)协会已将其纳入标准[5]。由于航空发动机管路系统多为薄壁管路，盲孔法属于有损检查，并不适用于其工况条件下的检测。X射线衍射法又局限于实验条件和其污染性，也不能做到工况条件的检测。根据盲孔法的测试原理，现提出高精度薄膜式应变片表面粘贴法作为航空发动机管路装配残余应力的检测手段。

由于航空发动机管路系统为薄壁管路，管壁厚度δ一般只有1mm左右。盲孔法中应力释放孔的孔深一般为1.5～3mm。这个数值大于航空发动机管路系统的壁厚。而通过这种孔深的盲孔法所测试的试件厚度一般在15mm以上，即盲孔孔深与被测件厚度的比值为1∶5～1∶10，这种测比下的测试结果一般精确可靠。那么，以同样的测试比例换算到航空发动机管路系统上时，所需的形变释放厚度就变成了0.1～0.2mm，其形变状况可以直接反应在测试区的表面上，即可通过在表面直接粘贴应变片的方式测得其应变变化量，再根据相应的公式就可计算出被测点的装配残余应力的大小。

2 实验研究

2.1 实验条件

由于航天发动机管路系统的设计遵循先进性和继承性原则，管路系统结构简单、尺寸小、质量轻，这使得管路系统中大部分的管路为薄壁细管。航天发动机管路一般使用不锈钢材料，如1Cr18Ni9Ti(SUS321型不锈钢)；当为提高管路的耐介质腐蚀能力时，多采用06Cr19Ni10奥氏体不锈钢代替碳钢管路；对于耐腐蚀程度要求更高的管路，如沿海边缘施工的管路系统项目，会选用022Cr17Ni12Mo2低碳奥氏体不锈钢[6]。航空发动机根据制造部位不同、工况环境不同等因素，材料的选用往往也会有所差异。

在实验选材方面，参考国内外同类管路材料中性能优异(耐腐蚀性能较好、强度和塑性指标较高)、工艺成型成熟的材料1Cr18Ni9Ti的管路作为实验对象。本文中所选用的是直径为Ø6mm、管壁厚度δ=1mm的1Cr18Ni9Ti不锈钢管路，管长分别为182mm与355mm。弯管接头采用304不锈钢直角管接头，如图2所示。

基于以上实验选材情况，有以下假定条件。

(1)管道为等截面、纯弹性、均质和各向同性的圆管；

(2)不同装夹位置的内应力大小相等；

(3)管路内流体稳定，忽略管道径向形变引起的流体径向运动及流体绕管轴的旋转运动。

考虑到航空发动机管路系统密集、薄壁等特点，结合盲孔法等残余应力的检测方法，针对航空发动机工况条件，本文采用意大利PANTHER油润滑型空气压缩机提供气体介质。通过专用应力检测传感器系统，对实验管路系统的应力变化及形变情况进行实时检测。具体实验原理如图3所示。

考虑到影响管路装配残余应力的因素较多，如管路系统中的介质、管路管径大小、卡箍型号质量等。为尽可能保证管路系统的可靠性，减少因系统自身误差对规律的影响，本实验采用同一厂家同一批次的型材管路，使用同批次管路接头、欧姆卡箍等成品零件，对实验模拟管路系统进行搭建，减少零件间存在的误差，以保证管路系统自身的误差最小。

根据材料力学原理及装配残余应力测试系统采用的应变片布片与接桥方案，对半桥测量载荷的情况进行理论分析，有R1趋近于ΔR；R2趋近于-μΔR，根据泊松比定义，可得到式(3)～(5)的计算公式。

(3)

(4)

(5)

式中：U为输出电压；U0为输入电压；n为桥臂系数；εD为仪器应变读值；εZ为受力真实应变值；σ为管路受到的应力；μ为材料泊松比；R1、R2、R3、R4分别为桥臂对应电阻的阻值，ΔR为应变片电阻变化值；E为材料弹性模量，本实验中E的值为206GPa。对于钢材，通常取μ=0.285。

据此，便可求出被测管路所受装配残余应力的标量根据公式(3)～(5)可知，装配残余应力与管路形变值大小的关系可看作与常数系数K相关的一元一次方程，其中K=E/(1+μ)，所以，研究装配残余应力的影响规律只需观测管路系统形变值即可。而作用在管路系统上的装配残余应力的大小则通过管路最终处于稳态时的形变值求得。

2.2 实验设备

考虑航天管路薄壁管的特点，参考盲孔法等残余应力测试方法的原理，本实验对于单管残余应力的测量采用直接在管路外表面粘贴应变片的方法测量。应变片选用BX120-3M型电阻应变片，应变片参数如表2所示。

表2 BX120-3M电阻应变片参数表

为控制外界施加载荷的均匀性，在管卡紧固时使用定力矩扳手，以精确提供恒定的紧固扭矩。

为提供稳定的气体载荷，选用意大利PANTHER油润滑型空气压缩机提供气体介质，空压机参数如表3所示。

表3 PANTHER油润滑型空气压缩机参数

2.3 气体载荷压强对装配残余应力的影响

为对管路系统中装配残余应力的影响因素进行解耦分析，先采用一维直通管路进行实验，在载荷类型、气体流量、温度等条件不变的情况下，改变管路中气体载荷的压强大小，测试管路中的应力应变值。实验参数如表4所示。

表4 不同气体压强下应力应变实验参数

将表4中条件下测试的数据整理，可得到如图4所示的变化曲线，曲线有如下规律：在相同的压强下，管路系统的形变会随着时间的增加而增大，当达到某一峰值后，形变-时间曲线会出现拐点，数据只在某一区间内波动，不再呈线性增长，管路系统会趋于稳定；而在压强增大时，这个拐点会延后，在足够长的时间内，管路系统还会趋于稳定，压强越大，趋于稳定时管路产生的总形变越大。

通过图4可看出，在0.2MPa压强下，管路在100min后达到形变峰值并趋于稳态，此时其形变值约为29μm；在0.4MPa压强下，管路在150min后达到形变峰值并趋于稳态(190min时的突变值由于环境振动导致，可排除)，此时其形变值约为38μm；在0.8MPa压强下，管路在200min后达到形变峰值并趋于稳态，此时形变值约为56μm。

根据式(5)，将各种条件下作用在管路系统上装配残余应力造成的形变值代入，可知σ0.2MPa=0.4809N，σ0.4MPa=0.6092N，σ0.8MPa=0.9619N。

2.4 冲击载荷下装配残余应力的影响

在2.3实验的载荷类型、温度、搭建方式等不变的基础上，取气体压强0.4MPa作为本实验中的气体压强值。在空压机与管路系统之间添加一个二位三通换向阀，以每分钟换向15次的方式为管路系统提供冲击载荷，测试在冲击载荷作用下管路中的应力应变值。实验结果如表5所示。

表5 不同载荷下应力应变数据对比表

将表5中条件下测试的数据整理，可得到如图5所示的变化曲线，曲线有如下规律：在0.4Mpa压强下，管路内气体载荷的类型并不影响其达到稳态后的总形变量大小，但相比于连续的气体载荷，冲击载荷下管路的形变量达到稳态的时间明显缓慢。

通过图5可以看出，在连续载荷作用下，管路在50min后达到稳态，此时形变值约为28μm；在冲击载荷作用下，管路在90min后左右达到稳态，此时形变值也在28μm左右。

根据式(5)，将各种条件下作用在管路系统上装配残余应力造成的形变值带入，可知σ冲击=0.4809N，σ连续=0.4889N

2.5 工况条件对装配残余应力的影响

在温度、载荷类型等条件不变的情况下，取气体压强为0.4MPa，仅改变管路系统振动环境，研究其影响规律。将管路系统放置于振动平台(振动频率为1000～1500Hz)，由振动平台提供振动频率，使管路系统台架振动，此时测试管路中的应力应变值，实验结果如表6所示。

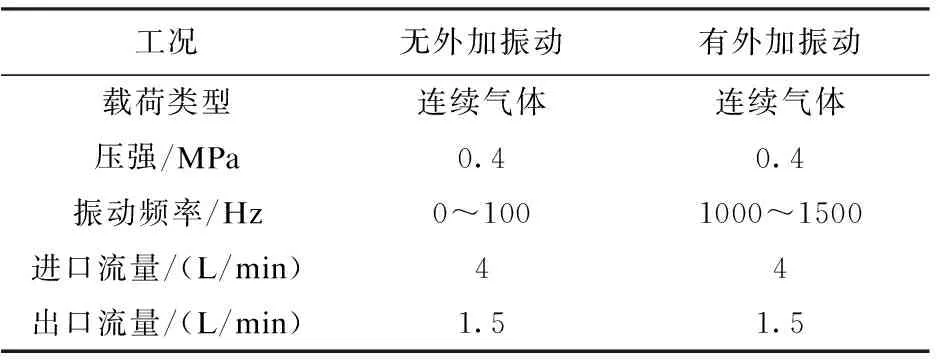
表6 不同工况条件下测试参数

将表6中条件下测试的数据整理，可得到如图6所示的变化曲线，曲线有如下规律：在相同压强下，管路系统的工况条件与总形变量大小无关，但在施加外部振动后，管路的形变速率明显升高。

通过图6可以看出，在无外加振动的作用下，管路在160min后达到稳态，此时形变值约为35μm；在有外加振动的作用下，管路在60min后达到稳态，此时形变值也在35μm左右。

根据式(5)，将各种条件下作用在管路系统上装配残余应力造成的形变值带入，可知σ有外加=0.6252N，σ无外加=0.6284N

3 实验结果与分析

当一维管路中存在装配残余应力时，管路存在微小的挠曲变形。而在工况条件下，由于气体载荷的存在，管路内存在压力，这种力与装配残余应力重叠，导致管路继续形变。相对于管路中心点位置，管路内压强增大，作用在装配节点上的力增大，使得其力矩增大，管路的形变增加。

冲击载荷的存在，使得原本存在装配残余应力的管路系统中的应力场不能处于平衡状态，这种冲击会使管路系统的形变瞬间增加，产生弹性形变，在无冲击也无流体的空白段内回弹，导致管路达到形变峰值的时间加长。

台架的振动会带来管路的同步振动，这种振动会与管路的装配残余应力形成正向影响，从而加快管路的形变。当装配残余应力释放后，管路系统的应力场处于动平衡状态，形变不再增加，所以峰值与无振动的管路系统相同。

4 结论

在不改变流量、温度、装配节点距离、管长、管径等因素的情况下，只改变气体压强、载荷类型及台架振动这三个影响因素中的一个因素时，可得出如下结论。

(1)气体压强增大，管路的形变峰值会随之增大，且达到稳态的时长也会随之增加；

(2)冲击气体载荷与连续气体载荷作用下管路系统所达到的形变峰值相近，但冲击气体载荷下管路达到稳态的时长较连续气体载荷下所用时长会有所增加；

(3)台架振动并不影响管路系统形变所达到的峰值，但会加快其变化速率，使管路系统在较短时间内到达稳态状态。