广义S变换与不同反射系数正演模拟

(成都理工大学 四川 成都 610059)

一直以来对于地震信号的处理分析都是基于传统意义上的标准傅里叶变换，单纯研究时间域的正交基必定会忽略信号源所释放的信息。Potter对人的声波信号进行了分析，将时间域的某一特定区段作为研究区段，称为谱图法，此法的函数进行开方即得到短时傅里叶变换的基函数。小波函数的作用就是剖析细小的变换，展现细节。分别在1988年和1994年Daubechchies和Geronimo将小波变换继续发展，多尺度的分析思想，、正交小波基函数和多小波的分析一一被提出证明并且加以运用，直至发展至今。S变换可由小波变换推算得，具有无损性，而广义S变换在S变换基础添加额外参数对原函数进行润色，既对不足加以补充，又对原有进行突出拓展。

一、方法原理

广义S变换原理是基于短时傅里叶变换和小波变换中的高斯窗函数得到的启示，是一种全新的视频分析方法，Gabor对傅里叶变换提出加窗形成基函数为：

wτ,ω(t)=w(t-τ)eiωt

(1-1)

张贤达定义短时傅里叶变换为：

(1-2)

重新定义调节时窗宽度的尺度因子为：

(1-3)

代入可得广义S变换：

(1-4)

当λ=1,p=1时，上式即为标准的S变换(Stockwell，1996)

(1-5)

二、模型测算

油气勘探中薄储层的识别勘探一直都是重中之重，Widess研究了薄层的调谐效应，定义了在介质中传播如果小于主波的波长的1/4的储层厚度即为薄层，并且论证了其极限分辨率为主波长的1/8。陈学华、熊晓军等对S变换进行了改进，使其更灵活的分辨薄互层通过时频域，其分辨能力达到小于1/8主波长的能力。为此设计了四种不同类型的薄层楔状体模型：

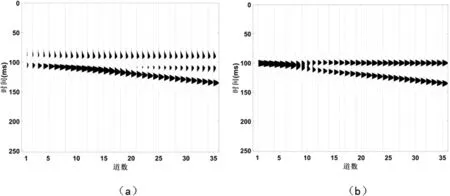
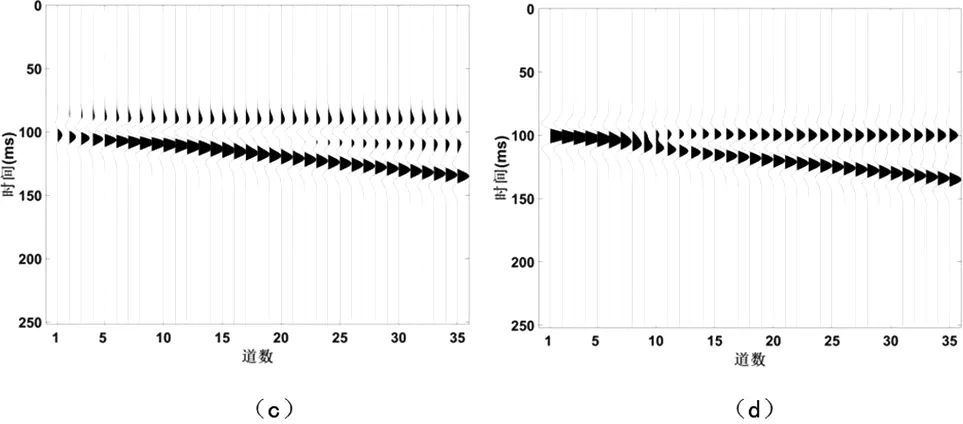
图2.1 四种不同反射系数模型

图2.2 四种模型广义S变换50Hz剖面

图2.1为不同反射系数组合的楔状体模型，均为250毫秒35道，三层介质，第一个界面位于100毫秒处，第二个界面由100毫秒随道数依次加一毫秒。图2.1(a)两界面反射系数作比为R=-0.1491/0.1491,(b)为R=0.0907/0.0907,(c)为R=-1034/0.1491,(d)为R=0.0620/0.0879。图2.2四幅图分别对应图2.1四种模型的广义S变换的50Hz单频剖面。

三、结论

由图2.1可发现上下界面不同反射系数组合对上下界面的分辨呈现不同状态，(a)、(c)较(b)、(d)更容易分辨。由图2.2可看出通过广义S变换对正演模型做时频分析可以很容易看出上下界面的能量团，对于图2.1中(b)、(d)在第9道区分的上下界面，广义S变换可以在第5道就可区分开，由此看出广义S变换在薄层分辨方面的能力。