基于改进粒子群算法的月地转移轨道优化

李远平，蔡远利，

(西安交通大学电子与信息学部，陕西，西安 710049)

近年来，国际上再次掀起月球探测高潮，美国、俄罗斯、中国、欧空局和日本都制定了各自的载人登月和月球基地计划[1]。我国原计划于2019年底实施“嫦娥五号”月球采样返回任务，轨道器与返回器组合体从月球停泊轨道加速后，进入月地转移轨道，在地面高度约5000 km处轨道器分离，返回器采用跳跃式再入，着陆场选择为中纬度的内蒙古四子王旗地区。月地转移轨道优化设计作为其中的技术难题之一，需要满足月球停泊轨道、月地转移和再入地球大气层等方面的复杂约束条件，尽量减小返回窗口内的逃逸速度增量，降低返回燃料消耗，同时获得最优的再入点参数，为跳跃式再入控制创造良好的起始条件。

月球返回轨道的设计方案可分为两种：一是月球自由返回轨道设计[2]，采用多段拼接方法[3]，适用于短期的月球探测返回任务；二是月地快速转移轨道设计，从月球停泊轨道加速后进入月地转移轨道[4]，适用于各类登月返回任务。文献[5]在圆形限制性三体模型下研究了地月空间对称自由返回轨道的设计方法及其轨道特性。文献[6]分析了地月自由返回时近地距的各种影响因素，包括出发时刻、转移时间、倾角组合等，提出了一种可使返回时近地距逐渐向设定的目标值靠拢的单向搜索方法。文献[7]分析了探测器低能量返回轨道的存在性与轨道动力学特性，提出了一种混合自适应遗传算法，用于寻找月球探测器返回地球所需的最低能量以及对应的转移轨道。文献[8―9]对从月球返回地球的轨道进行了分析，给出了快速月地转移轨道设计方法。文献[10]采用了自起步解析算法，构造出多次点火的轨道机动序列，可实现从任意近月停泊轨道到地球再入状态的转移，但在某些情况下需要消耗较多的燃料。

对于复杂约束条件下的优化设计问题，采用群智能优化算法具有明显的优势：算法结构简单、对初始值要求不高、不需要繁琐的公式推导。常用的群智能优化算法包括遗传算法[11]、模拟退火算法[12]、粒子群算法[13]、蚁群算法[14]、蜂群算法[15]、萤火虫算法[16]和离子运动算法[17]。

本文基于月地快速转移轨道的思想，建立了多段拼接的解析法轨道计算模型，考虑了月地转移轨道和再入弹道参数等诸多约束条件，以月球停泊轨道的逃逸速度增量最小为优化目标，提出了一种改进粒子群算法，求解月心真赤道坐标系内的逃逸点轨道参数，搜索最优的逃逸点时刻、升交点经度和纬度幅角。

1 月地返回窗口选择

月球停泊轨道通常采用圆轨道，轨道高度hMP和轨道倾角iMP(相对月球真赤道面)由月球轨道交会对接任务确定，月地返回窗口选择主要是确定逃逸点时刻tMP的取值范围，而逃逸速度增量ΔvMP、升交点经度ΩMP和纬度幅角uMP由下一步的月地转移轨道优化过程来确定。

利用喷气推进实验室JPL的DE/LE405历表来准确计算月球轨道位置及天平动参数，瞄准着陆场中心位置，考虑月地转移时间、地心段轨道倾角、返回当地时间和返回航程等约束条件，在一年或者更长的时间段内采用几何解析法进行覆盖式搜索。

2 月地转移轨道优化方法

2.1 轨道计算模型

在全局优化设计时，为了提高计算效率，采用双二体引力模型来描述月地转移轨道的运动规律。

1) 月球停泊轨道逃逸计算

先利用逃逸点时刻的月球停泊轨道参数，计算出探测器在月心真赤道坐标系内的逃逸点位置矢量rMP和速度矢量vMP，将其转换到J2000.0月心天球惯性坐标系，再考虑逃逸速度增量ΔvMP后，得到月地转移轨道的起始点位置矢量rM0和速度矢量vM0。

2) 月心段转移轨道计算

探测器从月球停泊轨道逃逸后，进入一条月心双曲线轨道。在月心天球惯性坐标系内计算探测器飞经月球引力影响球出口点的历元时刻tM1、位置矢量rM1和速度矢量vM1，将其转换到J2000.0地心天球惯性坐标系，得到相应的位置矢量rE1和速度矢量vE1。

3) 地心段转移轨道计算

探测器飞出月球引力影响球后，进入一条地心椭圆轨道。在地心天球惯性坐标系内计算开普勒轨道参数并推算至再入点，得到月地转移时间TET、地心轨道倾角iE、升交点赤经ΩE、近地点幅角ωE和近地点高度hEP，以及再入点历元时刻tR、当天时间τR、位置矢量rR和速度矢量vR。

4) 再入弹道参数计算

计算再入相对速度VR、再入角θR、再入点地理经度λR、再入点地理纬度φR、再入弹道面倾角iR和再入段航程LR。

2.2 优化目标函数

通常多目标优化问题可描述如下：

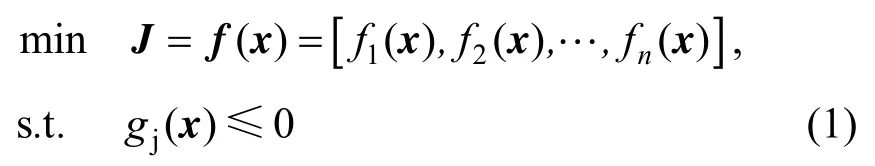
式中：x为决策向量，x∈Rm；J为目标函数向量，J∈Rn；fj(x)为目标函数；gj(x)为约束条件。

对于月地转移轨道优化问题，目标函数可简化为：

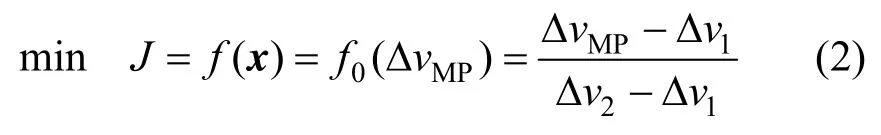
式中，Δv1、Δv2分别为月球逃逸速度增量的下界和上界。

约束条件如下：

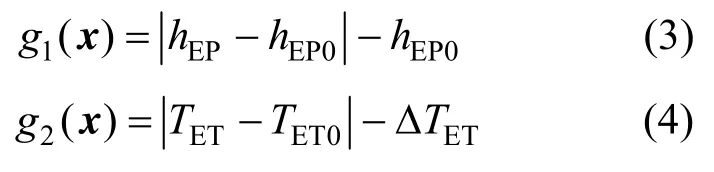
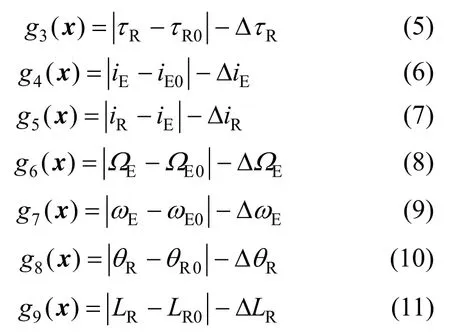
式中：hEP0为参考近地点高度；TET0为标称月地转移时间；ΔTET为月地转移时间偏差允许值；τR0为标称再入点当天时间；ΔRτ为再入点当天时间偏差允许值；iE0为标称地心轨道倾角；ΔiE为地心轨道倾角偏差允许值；ΔiR为再入弹道面倾角偏差允许值；ΩE0为标称地心轨道升交点赤经；ΔEΩ为地心轨道升交点赤经偏差允许值；ωE0为标称地心轨道近地点幅角；ΔEω为地心轨道近地点幅角偏差允许值；θR0为标称再入角；ΔRθ为再入角偏差允许值；LR0为标称再入航程；ΔLR为再入航程偏差允许值。

为了求解上述多约束条件下的优化问题，定义如下罚函数：

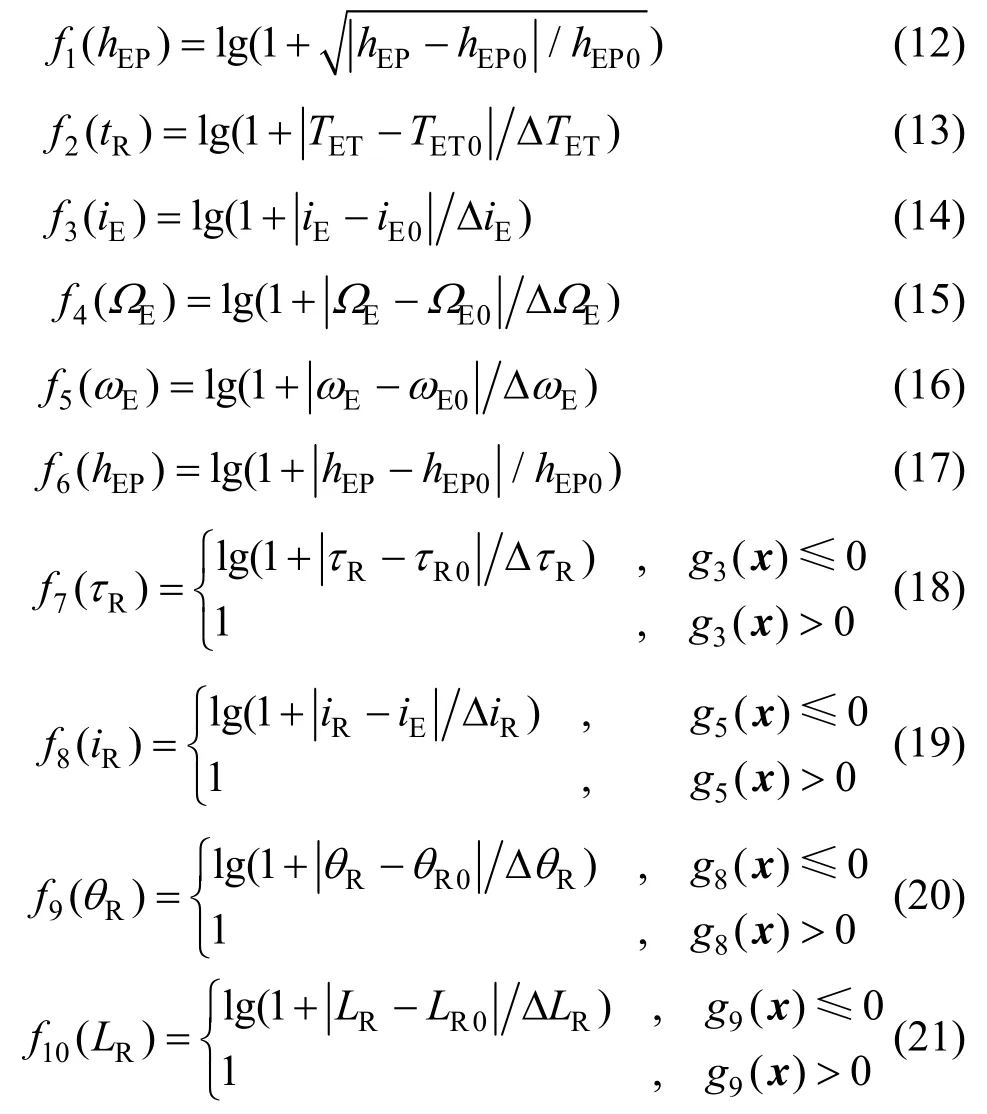
上述问题转化为：

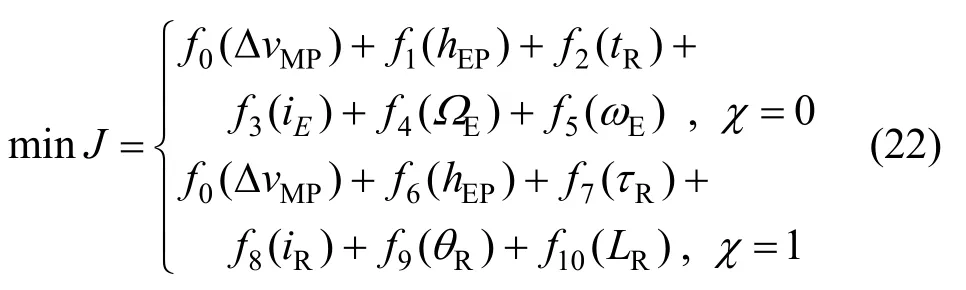
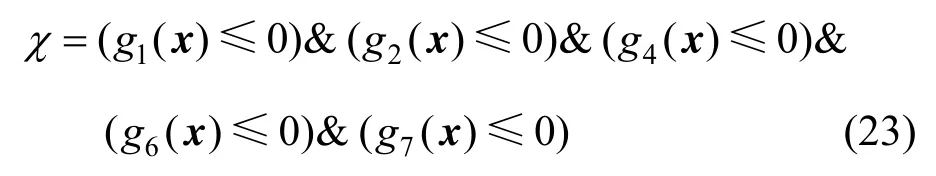
式中：χ为收敛域条件标识，0为不满足，1为满足。

2.3 优化求解方法

由于搜索空间大，约束条件多，目标函数复杂，本文提出了一种改进粒子群算法。

2.3.1 标准粒子群算法

粒子群算法(Particle Swarm Optimization, PSO)的基本概念源于对于鸟群捕食行为的简化社会模型的模拟，在解空间追随最优的粒子进行搜索[18]。

在PSO算法中，每个粒子在飞行过程所经历过的最好位置，就是粒子本身找到的最优解，称之为个体极值(pi)。整个粒子群所经历过的最好位置，就是整个群体找到的最优解，称之为全局极值(pg)。实际操作中，通过适应度值(fitness value)来评价粒子的“好坏”程度。

设粒子的群体规模为N，第j次迭代时第i个粒子的位置表示为，所经历过的“最好”位置记为，其速度表示为，群体中所有粒子所经历过的“最好”位置表示为。在标准PSO算法中，第i个粒子的速度和位置更新规则如下：

式中：j为迭代次数；c1、c2均为学习因子，取值为常数；r1、r2均为[0，1]区间上的随机数；w为惯性权重(Inertia Weight)。

设适应度函数为F(X)，第i个粒子个体极值的更新公式为：

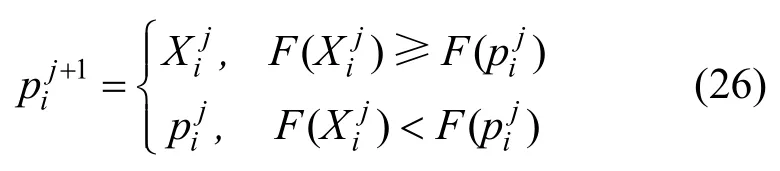
所有粒子的全局极值更新公式为：

标准PSO算法在应用时，存在收敛速度慢和早熟的缺陷[19]。

2.3.2 改进粒子群算法

为了克服标准PSO算法的缺点，针对上述月地转移轨道优化问题，提出一种改进粒子群算法(Modified Particle Swarm Optimization, MPSO)，利用适应度函数F(X)来更新惯性权重w，并对粒子的速度加以约束。

对于月地转移轨道优化问题，可将适应度函数F(X)的最大化变换为目标函数J的最小化。

对不同的粒子位置，采用不同的惯性权重

式中，JL为标函数的上限值，取值为10。

随着目标函数J的最小化，惯性权重→0，加快了粒子位置的收敛速度。

定义粒子的位置向量X为：

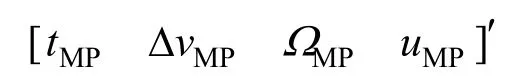
其搜索空间如下：

式中：[t1,t2]为月球停泊轨道逃逸点时间窗口；[Δv1,Δv2]为月球停泊轨道逃逸速度增量区间，[850,860]m/s；[Ω1,Ω2]为月球停泊轨道升交点经度区间，[0, 2π]；[u1,u2]为月球停泊轨道纬度幅角区间，[0,2π]。

粒子位置的初值为各维参数区间内的随机数组合，即：

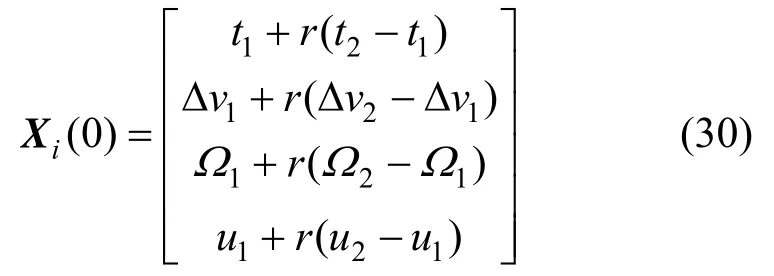
式中，r为[0，1]区间上的随机数。

粒子速度的初值为：

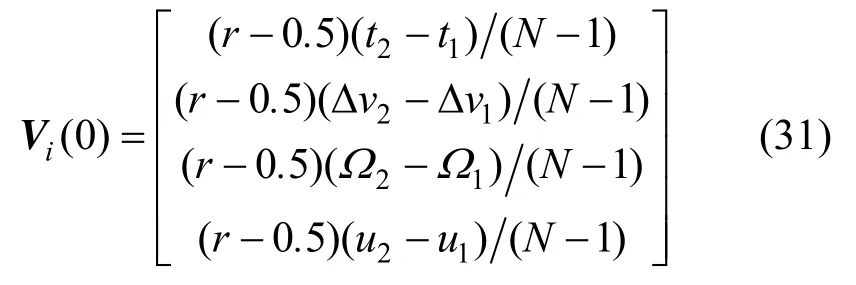
粒子速度的最大约束值为：

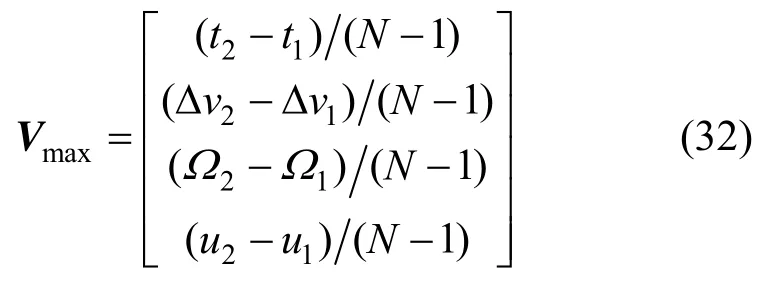
为进一步提高MPSO算法的收敛能力，利用月球停泊轨道逃逸点时刻tMP与再入点当天时间τR的相关性，当约束条件g2(x)≤0满足时，对第一维位置参数引入下面的随机反馈控制：

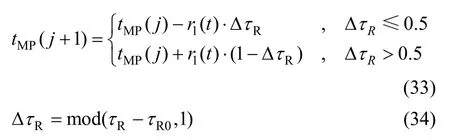
2.3.3 算法收敛性分析

利用式(24)进行位置更新的粒子，最终会收敛到一个稳定的位置[20]：

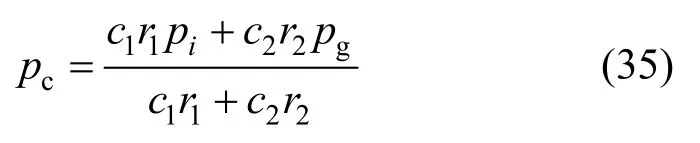
将式(35)代入式(24)中，可得：

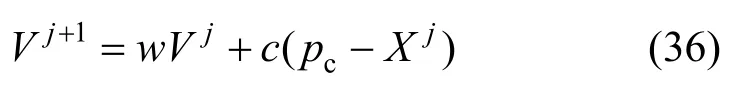
式中，c=c1r1+c2r2。

设yj=pc-Xj，算法的速度和位置更新公式可变换为：

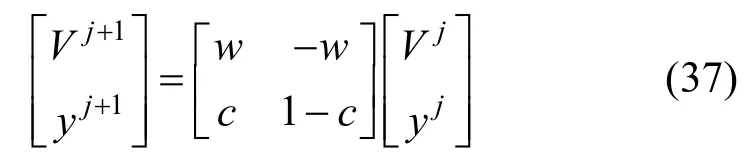
式(37)中，系数矩阵的特征方程为：

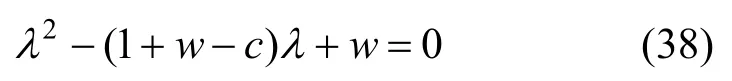
求解式(38)可得：

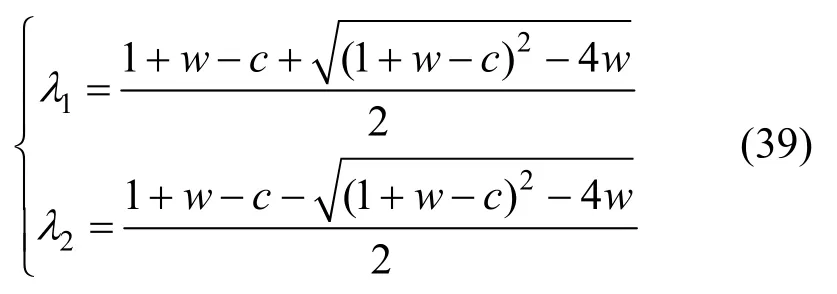
算法的收敛条件为max{|λ1|, |λ2|}＜1，代入式(39)可得：

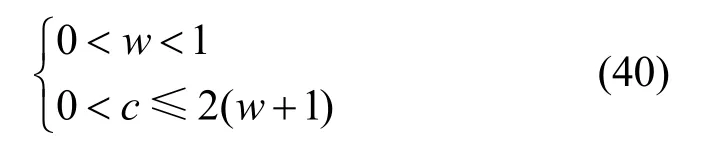
算法的收敛区域见图1。

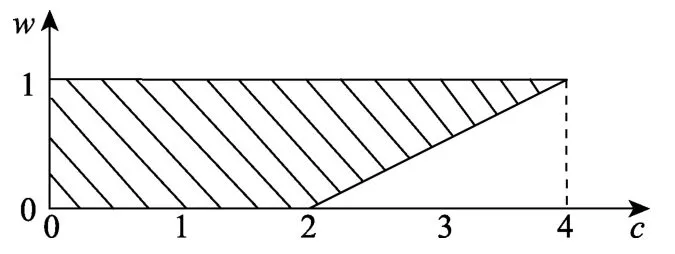
图1 改进粒子群算法的收敛区域Fig.1 The convergence region of MPSO algorithm

对于MPSO算法，由于w→0，当满足c1+c2≤2时，可保证收敛性。

3 算例及分析

利用本文所提出的MPSO算法进行月地转移轨道优化设计，所使用的计算机配置为2.53 GHz单核CPU、4G内存，编程环境为MATLAB 7.11.0。

设定月球停泊轨道高度hMP为210 km、轨道倾角iMP为45°，着陆场中心点地理经度λL=111.43°、地心纬度ΦL=42.16°，标称月地转移时间TET0=3.0 d、偏差允许值ΔTET=0.5 d，标称地心轨道倾角iE0=45.0°、偏差允许值ΔiE=3.0°，标称升交点赤经ΩE0=156.6°、偏差允许值ΔEΩ=10.0°，标称近地点幅角ωE0=10.8°、偏差允许值ΔEω=10.0°，参考近地点高度hEP0=45.0 km，标称再入点当天时间τR0=22:00:00(UTC)、偏差允许值ΔRτ=0.5 h，标称再入角θR0=-6.0°、偏差允许值ΔRθ=0.5°，标称再入航程LR0=6500 km、偏差允许值ΔLR=2000 km，再入弹道面倾角偏差允许值ΔiR=0.5°。

月地返回时间窗口为2017-01-30 03:00:00～2017-01-31 03:00:00(UTC)，粒子的群体规模数N为20。采用标准PSO算法，惯性权重w=0.73，学习因子c1=c2=0.75，搜索步数设置为300，运行一次计算程序耗时为54 s，部分粒子的目标函数值一度陷入局部极值，经过228步才收敛，但最终结果仍不满足全部约束条件，目标函数值搜索状态见图2。

采用MPSO改进算法，搜索步数设置为100，运行一次计算程序耗时为18 s。每次运行可获得一个优化结果，10次运行结果见表1。

综合MPSO改进算法的运行结果，最小收敛步数为21，最大收敛步数为68，平均收敛步数为38，月地转移轨道优化结果可归纳为两组，包含所有局部最优解，满足全部约束条件，见表2。两组优化结果的目标函数值相差仅为0.008，选取逃逸速度增量最小的第1组结果作为全局最优解。

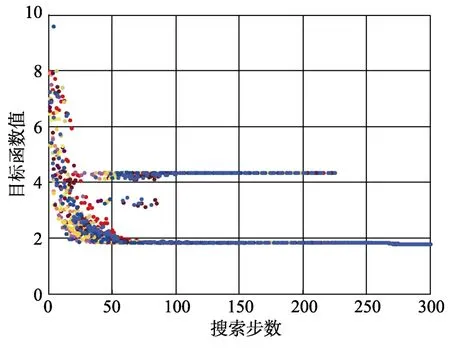
图2 目标函数值搜索状态(标准PSO算法)Fig.2 The search status of objective function(PSO)

一次轨道优化过程的目标函数值搜索状态见图3，逃逸速度增量搜索状态见图4。其中，经过25步搜索后，全部20个粒子收敛一致。

为验证上述优化结果的正确性，绘制出目标函数的全局等高线和曲面见图5、图6。

从图5和图6中，可以明显看到存在两组局部最优解，使目标函数达到局部极小值，与MPSO算法的优化结果一致，表明该算法对解决搜索空间大、约束条件多的月地转移轨道优化问题是正确有效的。

表1 10次MPSO算法运行结果Table 1 Ten computational results of MPSO algorithm

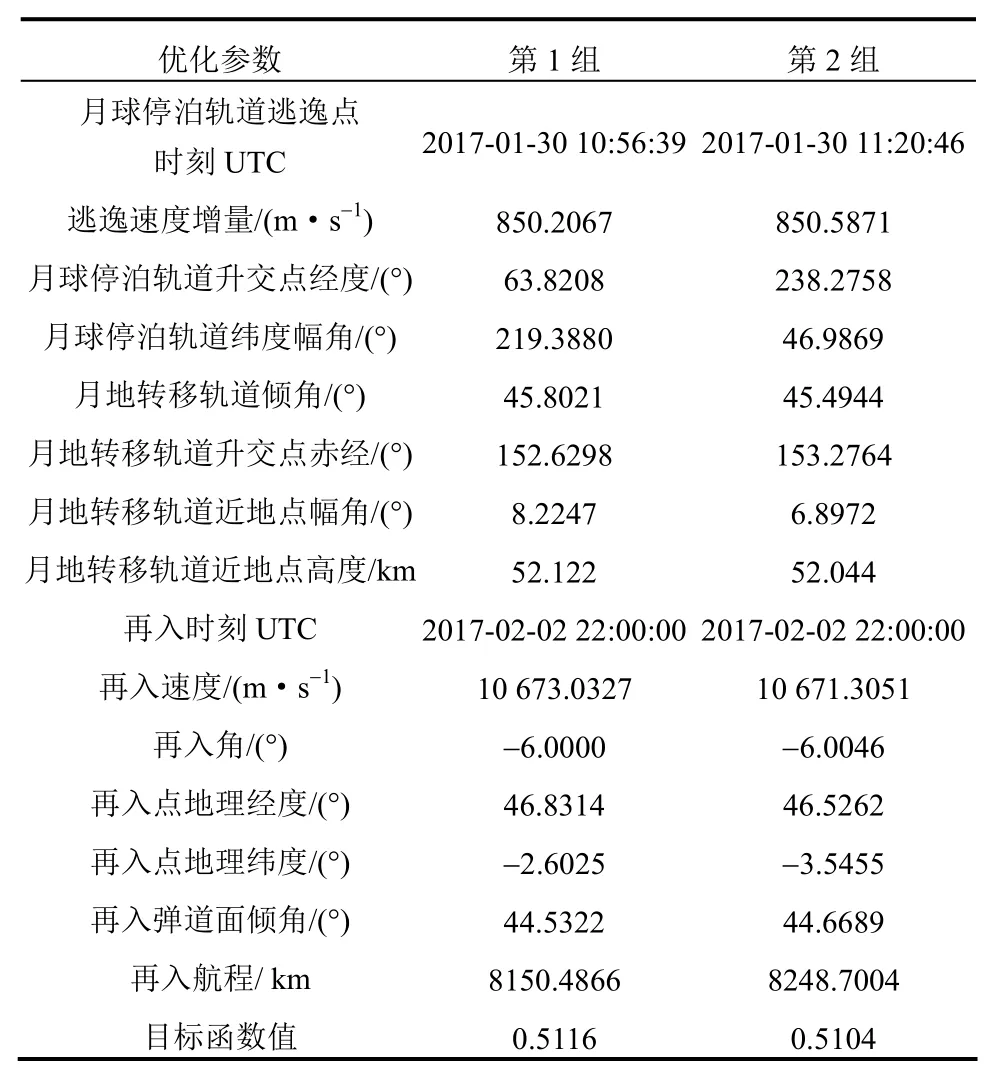
表2 月地转移轨道优化结果Table 2 The optimized result of moon-to-earth transfer trajectory

图3 目标函数值搜索状态(MPSO算法)Fig.3 The search status of objective function(MPSO)

图4 逃逸速度增量搜索状态(MPSO算法)Fig.4 The search status of escape velocity increment(MPSO)

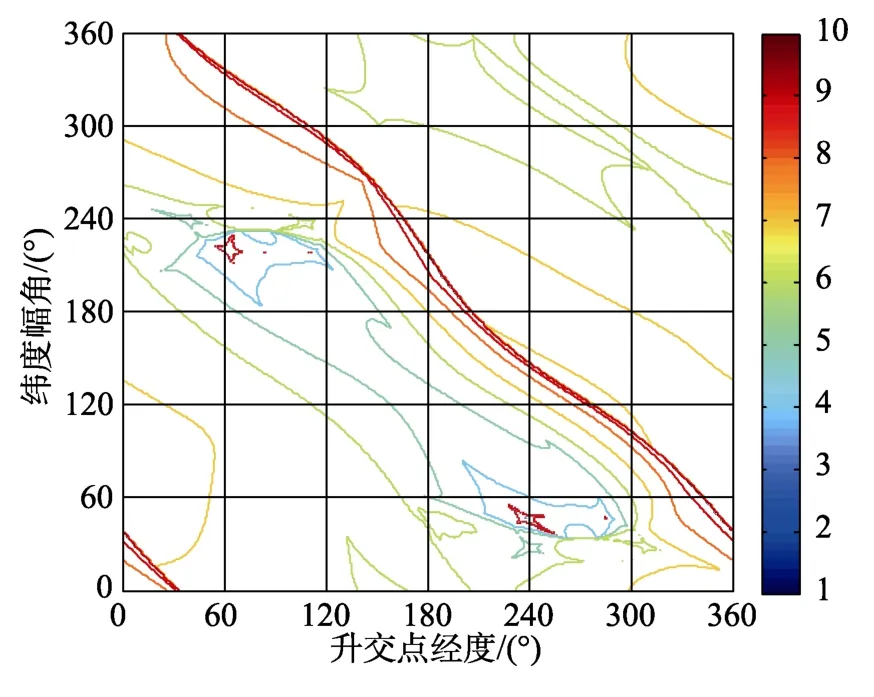
图5 目标函数全局等高线Fig.5 The contour map of objective function

图6 目标函数全局曲面Fig.6 The curved surface of objective function

4 结论

本文结合我国月球探测三期工程的实际需求，针对返回中纬度着陆场，考虑月球停泊轨道、月地转移和跳跃式再入等方面的复杂约束条件，提出了一种改进的粒子群算法，实现了返回窗口内逃逸速度增量的最小化，降低了返回燃料消耗，有效解决了多约束条件下的月地转移轨道优化问题：

(1) 通过罚函数法将多约束条件下的月地转移轨道优化问题转化为无约束优化问题，在收敛域内外使用不同的目标函数，便于采用粒子群算法进行优化求解。

(2) 用标准PSO算法求解月地转移轨道优化问题时收敛较慢且最终结果仍不满足全部约束条件，采用MPSO改进算法后能够较快收敛且满足全部约束条件，表明改进算法对解决复杂优化问题的有效性。

(3) 在预定月地返回时间窗口内，月地转移轨道优化的多次运行结果可归纳为两组，逃逸速度增量最小的那组结果是全局最优解。

(4) 通过目标函数的全局等高线和曲面图分析，验证了优化结果的正确性。

本文提出的优化方法，具有求解效率高、收敛性好、适应性强等优点，能够有效避免陷入局部极值，可适用于解空间有界的多参数优化问题。