移动型下击暴流及其作用下高层建筑风荷载的数值模拟

2020-03-16黄国庆赵丽娜

工程力学 2020年3期

李艺，黄国庆,2，程旭，赵丽娜

(1.西南交通大学土木工程系，成都 610000；2.重庆大学土木工程系，重庆 400000；3.资阳市自然资源和规划局，资阳 641300)

下击暴流是一种突发性强的小尺度局地强风，其近地面风速可达75 m/s，严重威胁到输电线塔和高层建筑等结构的安全。例如，澳大利亚等国80%的输电线塔坍塌与下击暴流相关[1]。下击暴流风垂直撞击地面后形成沿地面向外扩散的高强风，风从下击暴流中心处向外直吹，具有很强的破坏力。因地面不光滑，阻碍了径向风的流动，气流风向会因此发生变化产生竖向分量风，对建筑屋盖等影响较大。下击暴流风在撞击地面的过程中，射流口还在发生着水平方向的运动，造成地表附近的风向变化加剧，使其具有较强的下沉气流和低空风切变，在极短时间内产生极大的破坏力，对大跨、高耸结构、输电线塔、风机等造成严重破坏。对高层建筑等结构而言，下击暴流引起的荷载与常规风差异较大，下击暴流作用下结构的动力响应比大气边界层风作用下的结构动力响应大的多，例如下击暴流作用下建筑屋盖中心处位移接近于常规风作用下位移的2倍[2]。但中国荷载标准规范仅提供了常规风荷载，对下击暴流等特殊风并未考虑。由于下击暴流的危害性以及规范指导的局限性，因此，研究下击暴流风特性及其风荷载特性具有重要的现实意义，可为实际工程的抗风设计提供参考。

下击暴流的频发引起了越来越多学者的关注。对下击暴流的研究方法主要分为现场实测、风洞试验、数值模拟及理论研究四大类。在现场实测方面，Fujita[3]在NIMROD和JAWS项目中对下击暴流进行了现场实测，依据实际观测结果分析了下击暴流的流场特性；Hjelmfelt[4]描述了在科罗拉多州观测到的微暴流的形态，根据统计资料总结了微暴流的基本特征；Mccarthy等[5]调查了1982年夏天在美国丹佛斯台普顿国际机场发生的微下击暴流事件，详尽的描述了下击暴流的危害；黄国庆等[6]通过实测，发现在山区下击暴流频繁发生，这对山区大跨度桥梁、输电线塔及风机的抗风设计提出了新的挑战。

Chay和Letchford[7]开展了物理实验，研究在静止型下击暴流作用下立方体上的压力分布特征；Choi[8]利用稳定的冲击射流模型对下击暴流进行了模拟实验研究以确定地面粗糙度对其风剖线的影响；Zhang等[9]通过风洞实验研究了高层建筑距下击暴流射流中心不同位置处的风荷载；Jesson等[10]通过物理试验分析了瞬态下击暴流作用下建筑表面瞬时风压分布情况。

随着计算机的发展，数值模拟方法也被广泛应用于风工程研究。Selvam和Holmes[11]使用二维k-ε模型模拟了静止下击暴流撞击地面的过程；Shehata等[12]通过比较下击暴流与常规风对输电线塔作用效应的差异，揭示了在结构设计时考虑强荷载的重要性；Sengupta和Sarkar[13]利用多种湍流模型模拟了下击暴流风场，对比了数值模拟与试验结果的差异，探讨了对下击暴流数值模拟的最佳湍流模型、边界条件和计算域；李朝[14]采用三维稳态轴对称模型对静止型下击暴流进行了数值模拟，分析了下击暴流竖向风速剖面的相应特征；党会学等[15]进行了全尺寸下击暴流CFD数值模拟，据此提出了移动下击暴流风剖面的非线性预测方法；Huang等[16]基于RANS对下击暴流进行了数值模拟，研究了静止型下击暴流风场作用下高层建筑表面的压力系数分布；Chowdhury等[17]通过数值模拟描述了下击暴流的结构和演变过程，并与现有的全尺度数据进行了比较；胡伟成等[18]对山丘地形风场进行了数值模拟，揭示了大涡模拟能有效得出山丘地形下脉动风特性；Yumi和Yasushi[19]利用大涡模拟方法研究了强风产生的机理，并阐明了下击暴流诱导风荷载的特征。

为了便于使用，基于前述研究，学者们提出了多个经验模型，特别是针对风剖面的模型。基于轴对称下击暴流的假设，Oseguera和Bowles[20]提出了一种圆柱坐标系下的三维稳态下击暴流径向风速的分析模型，随后Vicroy[21]基于现场实测改进了其径向风速形状函数，此更新的模型被命名为OBV模型；Holmes和Oliver[22]在风暴中心移动基础上，通过大量数据的拟合给出了径向风剖面的经验模型；Li等[23]考虑了特征高度的非线性效应，修订并更新了 OBV 模型；宋淳宸等[24]利用多元EMDAM/FM分解得出了模拟多点非平稳下击暴流风速的方法。

本文基于冲击射流模型和雷诺时均方法对下击暴流进行了数值模拟，重点研究了移动型下击暴流对高层建筑的风荷载作用：首先，对静止型下击暴流及其作用下高层建筑的风荷载进行了稳态数值模拟，并将模拟结果与风洞试验对比，验证了计算模型及方法的可行性；然后，借助滑移网格技术对移动型下击暴流进行了数值模拟，并将两种状态的下击暴流进行了详细的对比，研究了移动型下击暴流的风场特性及其对建筑的影响。

1 静止型下击暴流数值模拟

基于RANS对静止型下击暴流进行三维稳态数值模拟，将数值模拟结果与Zhang等[9]的风洞试验结果进行对比，目的是为了验证本文数值模拟方法的可靠性，以便将其扩展到移动情况，并将模拟的结果与后续移动型下击暴流的结果进行对比研究。

1.1 静止型下击暴流风场数值模拟

计算模型如图1所示，整个风场模型尺寸为20D×20D×6D，射流管直径D=0.61 m(几何缩尺比为1∶650)，射流管高度H=2D，射流口速度Vjet=13m/s(速度缩尺比为1∶6)，网格为六面体结构化网格，利用O-Block生成射流口中心网格。对网格无关性进行验证后，采用的网格示意图见图2，首层网格尺寸为3×10-5m，本次数值计算的网格数量为900万。进行数值模拟时，离散化设置如表1所示，湍流模型采用SSTk-ω模型，压力速度耦合求解采用SIMPLEC算法，本文的数值模拟均在ANSYS/FLUENT平台下进行。本文稳态模拟下亚松弛因子参数值保持默认值，如表2所示。

图1 风场计算域剖面图Fig.1 Profile of wind field calculation domain

图2 网格示意图Fig.2 Grid schematic

表1 离散化设置Table 1 Setting of discretization

表2 亚松弛因子设置Table 2 Setting of under-relaxation factors

将本文得到的径向风速的竖直剖面与已发表论文中的风洞试验结果[25-27]及数值分析结果[28]相对比，图3表明了数值模拟的结果吻合度较好，证明本文模型以及模拟方法是可行的。

图3 与其他学者试验、数值模拟结果对比图Fig.3 Comparisons with experimental and numerical results of other scholars

1.1.1 径向风速剖面

图4描述了下击暴流风场不同径向位置r处的径向风速Vr沿竖向高度z的变化规律：同一径向位置处径向风速Vr随着高度z的增加急剧增大到最大值，并在一段高度内保持着极值速度，后随着高度的增加而减小。径向距离越远，极值速度持续的时间越短。图5描述了不同高度z处径向风速Vr随径向距离r的变化情况：同一竖直高度处径向风速Vr随着径向距离r的增加先线性增长，随后风速减弱。随着高度的增加，最大风速值点距离风口越近。从下击暴流径向风速的竖直剖面和水平剖面图中可以看出，径向峰值风速出现在近地面z=0.02D～0.06D，r=0.8D～1.2D范围内。

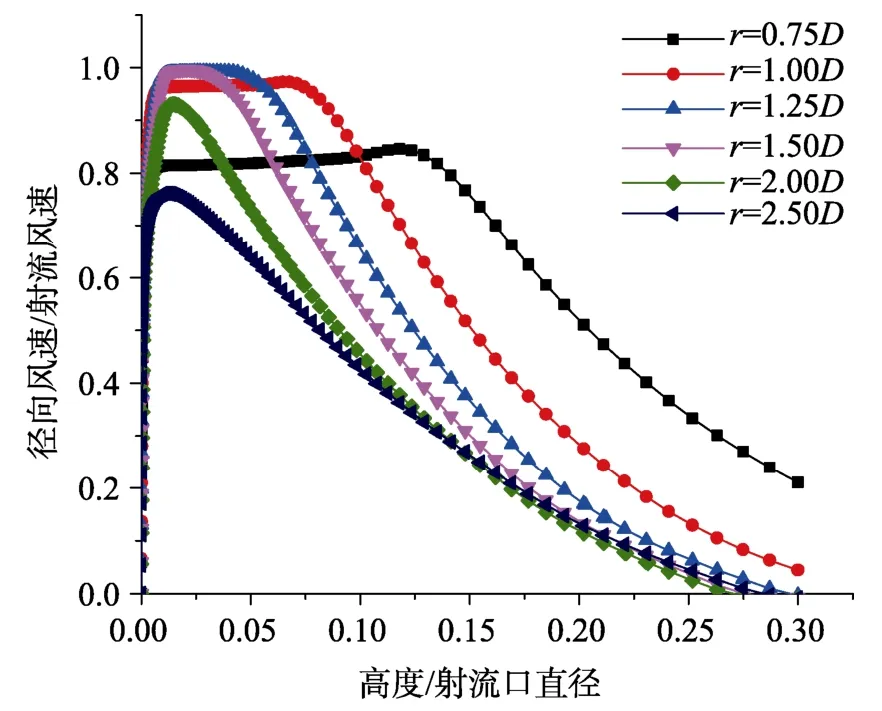
图4 径向风速竖直剖面Fig.4 Vertical profiles of radial wind speed

图5 径向风速水平剖面Fig.5 Horizontal profiles of radial wind speed

1.1.2 下击暴流的特征高度分布

OBV(Oseguera and Bowles/Vicroy)模型[21]认为边界层厚度随着径向距离的增加而缓慢的线性增长。通常采用最大水平速度对应高度Zm以及1/2最大水平速度对应高度δ来描述下击暴流边界层厚度，但由于Zm太靠近地面难以测量，既敏感又不稳定，通常选用δ来描述下击暴流的边界层厚度。

从图6可以看出CFD模拟的结果与Sengupta和Sarkar[13]提出δ的径向形状函数公式所得到的结果变化趋势一致，表明边界层的发展并不是呈线性增长，边界层特征长度是随径向距离的增大先减小后增大。

图6 下击暴流的特征高度δ分布Fig.6 Distribution of characteristic height of downburst

1.2 静止型下击暴流对高层建筑作用的数值模拟

从下击暴流径向风速水平剖面模拟结果表明：风速峰值基本出现在距射流中心r=1.0D附近。因此，将尺寸为45 mm×45 mm×180 mm的高层建筑布置在距射流中心1.0D处，如图7所示。计算模型和参数设置同前，建筑物表面采用无滑移壁面边界。

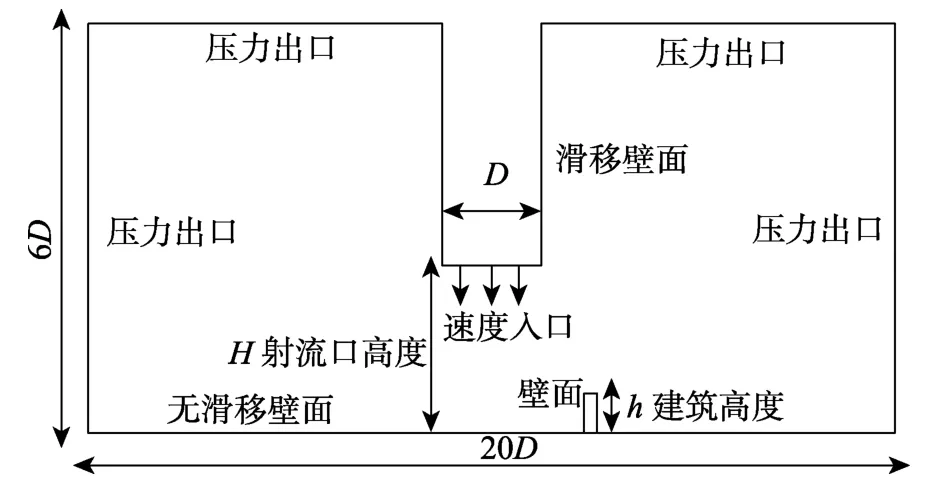
图7 计算域剖面图Fig.7 Calculation domain profile

1.2.1 壁面压力系数分析

射流垂直喷射，在壁面形成一个核心高压区。从图8可以看出，在壁面射流口中心处压力系数最大，壁面压力系数约为1.0，在r=1.0D附近，壁面系数减小到0。正压区域直径约是射流口在壁面上投影直径的2倍。

图8 壁面压力系数分布Fig.8 Distribution of wall pressure coefficient

1.2.2 建筑物表面局部压力系数

在z=0.25h(h为建筑模型高)高度处从建筑物迎风面中心到背风面中心逆时针等距布置 19 个监测点，见图9。将本文模拟得到的压力系数与Zhang等[9]的静止型下击暴流试验结果进行对比，压力系数变化规律基本一致，模拟的结果有较好的吻合度。从图9可以看出：建筑物迎风面的压力系数为正，在中心处达到最大，从中间向两边递减，侧面和背面的压力系数为负，背面的压力系数略微小于建筑物侧面压力系数值。模拟得到侧面压力系数绝对值小于试验值，这可能是由于采用稳态模拟，侧面的涡环较弱造成的。

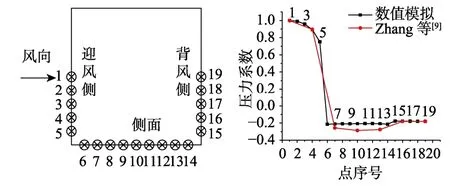
图9 建筑表面固定高度处压力系数对比Fig.9 Comparison of pressure coefficients at fixed height of building surface

1.2.3 建筑迎风面中线压力系数

图10描述了建筑迎风面压力系数随高度的变化趋势：在建筑物迎风面底部出现一段高压区，在一定高度范围内压力系数保持Cp极值不变，后随着高度的增加而减小，主要是因为下击暴流的强风速一般出现在近地面附近。

图10 建筑迎风面中线压力系数随高度的变化Fig.10 Variation of centerline pressure coefficients of building windward surface with height

1.2.4 层间力

将建筑模型均分为10层，数值模拟计算各层层间力，层间力系数计算结果见表3。从表3可以看出，建筑模型表面横风向气动力明显小于顺风向气动力系数。将所得到的顺风向气动力系数CFr与Zhang等[9]的试验结果进行比较，结果见图11。可以看出，虽然CFD模拟的阻力系数结果小于试验所得到的结果，但各层阻力系数的变化趋势是一致的，阻力系数随着高度的增加先增大后减小，约在z=0.3h处风力系数达到最大，这与前文的风速变化趋势吻合。本文采用的几何缩尺比为1∶650，因此，在结构设计时要注意下击暴流对35 m建筑高度处的破坏。

表3 层间力系数值Table 3 Interlayer force coefficients

1.2.5 模型表面压力系数云图

图12为模型表面压力系数云图。从图12(a)可以看出，建筑物顶面压力系数为负值且数值较小。图12(b)显示迎风面压力系数为正值，分布呈对称性，同一竖向高度处，中心线上压力系数最大，压力系数随高度的增加先保持着较大值不变而后减小。图12(c)表明背面的压力系数为负值，压力系数随高度的增高先增加后减小，由于流动在背面中心处发生了再附着，造成背面两侧压力系数较大，中心压力系数较小。

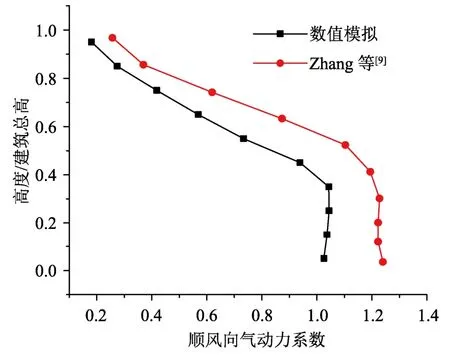
图11 层间阻力系数分布Fig.11 Distribution of interlayer drag coefficients

图12 模型表面风压分布Fig.12 Wind pressure distribution on model surface

1.2.6 不同风向角下模型表面压力系数

选取0°、15°、22.5°、45°风向角来衡量不同风向角对建筑表面压力系数的影响，建筑物整体阻力系数见图13，侧面压力系数云图见图14。从图中可以看出，与常规风情况相似[29]，当风向角为15º时会产生一个明显的涡，侧面出现一个最大负压，约为-1.09。此时整体阻力系数最大，但各角度下的值差异不大，这与Zhang等[9]的试验结果相吻合：当建筑物位于r=1.0D时，风向角对风力系数的影响较小。

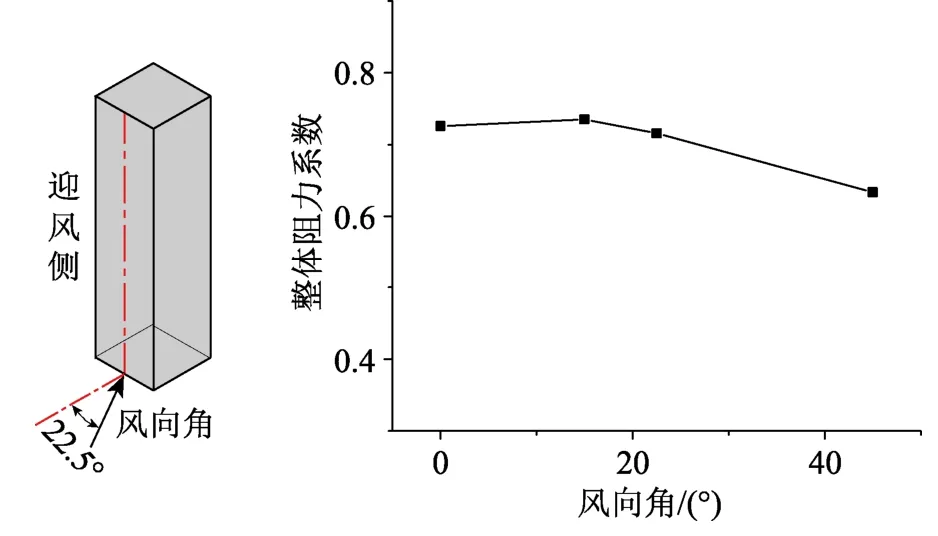
图13 各风向角下建筑模型的整体阻力系数Fig.13 Overall drag coefficient of building model under each wind direction angle

图14 侧面压力系数云图Fig.14 Lateral pressure coefficient cloud

2 移动型下击暴流数值模拟分析

现场实测数据[30]说明，俯冲气流下沉撞击地面的过程中，射流中心并不是固定不动的，射流口的移动会增强运动方向上的水平风速，更容易造成建筑物的破坏。

2.1 移动型下击暴流风场数值模拟

采用滑移网格技术以及瞬态计算方法可更加接近真实的模拟下击暴流风场。计算域设置为22D×22D×6D的长方体区域，射流管直径以及高度、射流速度同前。Holmes[31]推算下击暴流的移动速度范围为10 m/s～20 m/s，根据速度缩尺比1∶6，本文模拟选取移动速度为Vt=2 m/s。模型计算域见图15，设定时间步长为0.001 s，边界条件、湍流模型等同前。

滑移网格是一种能精确求解多运动参考系问题的技术，采用2个或多个网格区域来进行计算模拟。本文采用两个独立文件分别生成静网格和动网格区域，在计算开始前将网格文件进行合并，相邻区域间采用分界面Interface进行分隔，相邻区域一侧的网格沿着网格分界相对于另一侧区域进行滑动。本文采用铺层方法来实现射流口的移动，通过在边界层创建新的网格来完成运动区一侧的扩展，通过边界层网格的消除来完成另一侧运动区的收缩，并重新建立网格之间的连接关系，凭借分割与合并因子来保证铺层效果。由于流动的非稳态特性，因此，在计算中需要使用瞬态分析。计算模型如图15所示，动网格区划分为刚体运动区域及变形区域。射流口从起点O沿x轴正方向匀速运动到终点O＇，移动距离为10D，速度由UDF(user defined function)定义。

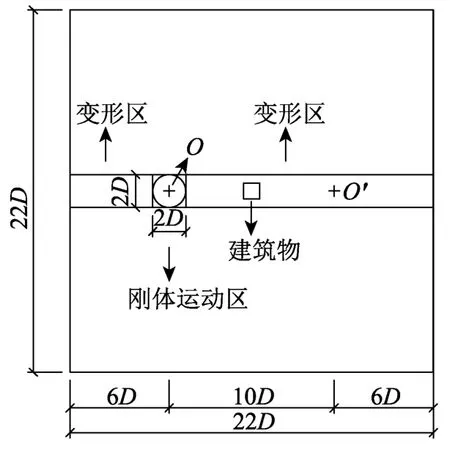
图15 计算域示意图Fig.15 Schematic diagram of calculation domain

将本文模拟得到的水平风速竖直剖面与Chen等[32]的模拟结果以及Holmes等[22]的经验模型进行对比。图16可说明本文数值模拟的结果吻合度较好，数值模拟的结果可靠。本文模拟的结果的极大值与Chen等[32]论文结果的极大值有微小差异，这是由于选取的下击暴流移动速度不同造成的，本文选取的移动速度为2 m/s，按1∶6速度缩尺比换算后为12 m/s，Holmes和Oliver[22]选取的移动速度也为12 m/s，Chen等[32]选取的移动速度为10 m/s，可看出移动速度越高，风速峰值越大。

2.1.1 径向风速特征

各时刻的速度云图可清晰描述下击暴流由积云阶段到成熟阶段的发展过程，图17显示了主要代表性时刻对应的速度云图。0.5 s以前处于下击暴流的积云阶段，环形涡还未到达壁面，下沉气流未完全发展；在0.5 s时，第一个涡流接触地面，气流快速分散，形成径向风速；从0.5 s～1.0 s是涡流到达地面后的充分发展阶段，影响区域不断扩大；从1.0 s～3.0 s速度云图没有太大变化，可认为移动型下击暴流已进入成熟阶段。

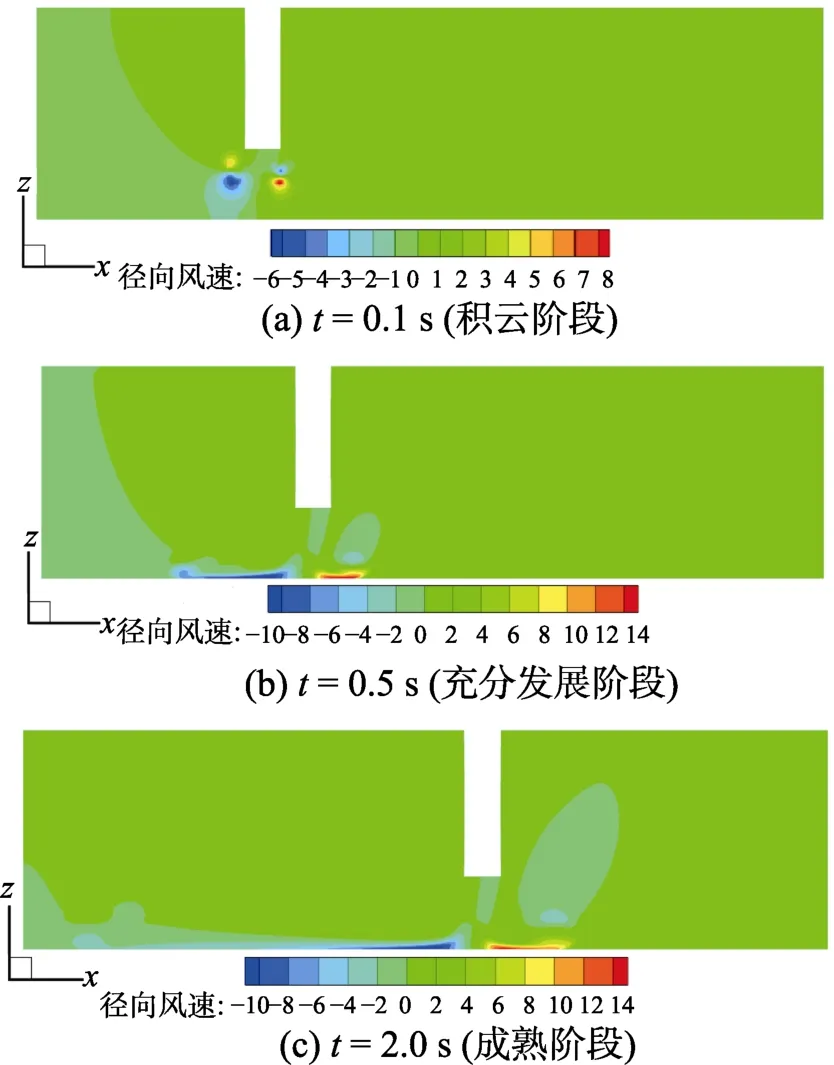
图17 代表性时刻对应的速度云图Fig.17 Speed contour corresponding to representative moments

图18描述了高度z=0.03D处不同时刻移动型下击暴流对应的径向风速剖面。从图18可看出，在积云阶段，下击暴流发展并不充分，该阶段径向风速值较小，成熟阶段后径向风速增强，风速极值趋于稳定，不同时刻径向风速剖面极值大小基本相同。

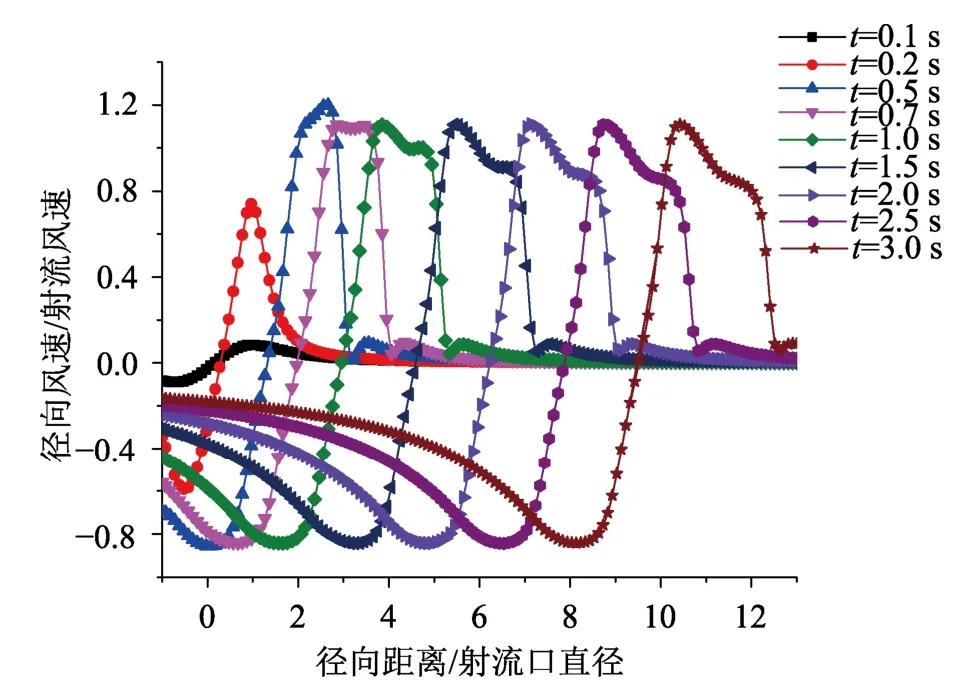
图18 不同时刻移动型下击暴流径向风剖面Fig.18 Radial wind profile of downburst at different times

选取达到稳定状态的移动型和静止型下击暴流的径向风速剖面进行对比，结果见图19。两运动状态下径向风速剖面的变化规律基本一致。从图中可以看出，静止型下击暴流正负风速极值大小一致，而移动型下击暴流的负风速极值小于正风速极值，下击暴流的移动增强了运动方向上的径向风速，减弱了负方向的径向风速。

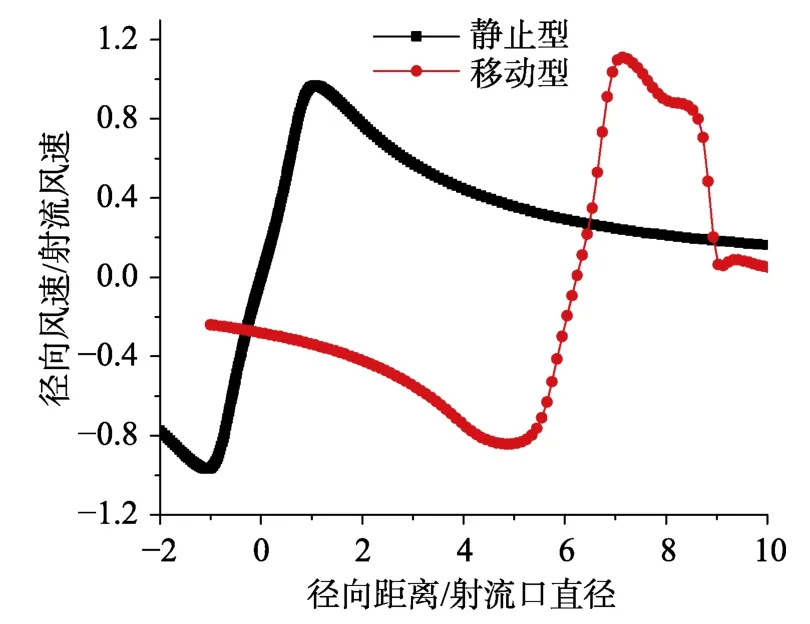
图19 移动型与静止型下击暴流径向风速剖面对比Fig.19 Comparison of radial wind profiles between moving and static downbursts

2.1.2 风速时程曲线

时程曲线中时间轴可通过公式向空间轴进行转化,转化公式如下：

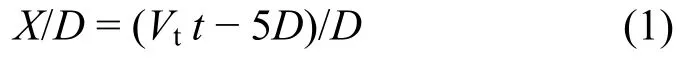
式中：X为距风场中心的水平距离；t为射流中心移动的时间。

通过公式转化后，横坐标0点位于计算流域中心处。监测风场中心处距离地面高度z=0.03D点的风速时程曲线，如图20所示。可看出风速的变化符合如下规律：射流口靠近过程中，监测点的径向风速逐渐增大，达到风速峰值后风速减弱，随着射流口的继续移动，径向风速增加，出现二次峰值。射流口远离监测点的过程中，负向风速增加，约在距离测点0.75D处达到负向风速极值，随后负向风速减弱最后速度值趋于0。这与图21中Holmes和Oliver[22]参考安德鲁斯A.F.B.冲击风实地观测数据[33]进行模拟得到的风速时程曲线变化规律吻合。

图20 射流口处于风场中心某一固定高度观测点不同径向位置时监测点的风速变化Fig.20 Wind speed variation at a fixed height in center of wind field at different radial positions of jet nozzle

图21 安德鲁斯A.F.B.下击暴流的模拟风速记录Fig.21 Simulated wind speed and direction records for Andrews A.F.B.downburst

2.2 移动型下击暴流对高层建筑作用的数值模拟

下击暴流的移动增强了运动方向的风速值，建筑物表面的风压会有所增大，研究移动型下击暴流对建筑物的作用效应对结构的抗风设计至关重要。本节将建筑物布置在计算流域中心处，见图15，其他参数条件同上。

2.2.1 壁面压力系数分析

当t= 2 s时，射流中心移动了6.56D，将此时射流中心坐标作为原点坐标，进行局部放大，结果见图22。与静止型下击暴流相比，下击暴流正压核心区域缩小，在X=0.5D附近，压力接近于大气压，正压区域约等于喷射口投影到壁面的范围。距射流口中心1.3D处，壁面出现负压，并随着距射口投影中心的距离的增加负压增大，在距射流口中心约为2D处负值达到最大，随后距离喷射口投影中心越远，负压迅速减小接近于0。

图22 2 s时壁面压力系数分布Fig.22 Distribution of wall pressure coefficient at 2 s

2.2.2 压力系数时程曲线

由于建筑的对称性，只选择在建筑物顶面一侧设置了6个观测点，测点布置如图23所示。随着下击暴流的靠近，建筑表面出现负压，且随着距离的靠近，负压值增大，约在距建筑1.5D范围处达到最值，随后压力系数绝对值减小。当下击暴流运动到建筑物上方时，顶面压力系数变为正值并逐渐增大，约在建筑正上方附近达到峰值，后随着下击暴流的远离，压力系数减弱。从图23可以看出，顶面中心压力系数最大，迎风侧和背风侧其次，侧面的压力系数最小。

图23 建筑物顶面监测点的压力系数时程曲线Fig.23 Pressure coefficient time history curves of monitoring points on top of building

分别在建筑物正面和背面中心线上高度z=1/3h、z=1/2h、z=2/3h处各设置3个观测点，图24描述了建筑物迎风面压力系数的变化情况：随着射流口距建筑的径向距离缩短，迎风面的压力系数逐渐增大，当射流口到达建筑正上方时，压力系数达到峰值，随后随着射流口的远离而减小，当距建筑物1D距离时，压力系数由正变为负且逐渐增大，在r=2D时，达到吸力达到峰值。射流中心与建筑物的距离为−1D～2.5D时，移动型下击暴流对建筑物迎风面影响较大。

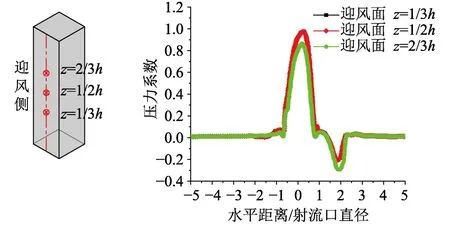
图24 建筑物正面监测点的压力系数时程曲线Fig.24 Pressure coefficient time history curves of monitoring points on front surface of building

图25描述了建筑物背面压力系数的变化情况：在下击暴流风口距建筑物−2D时，建筑物背风面压力系数出现负值，随着射流口的靠近，压力系数绝对值增大，在1D时达到峰值。在下击暴流到达建筑物正上方时，压力系数变为正值并逐渐增加，在远离建筑物1D时，压力系数达到最大值，最后随着下击暴流的远离，背面压力系数减弱直至为0。射流中心与建筑物的距离为−2D～2D时，下击暴流对建筑物背面影响较大。

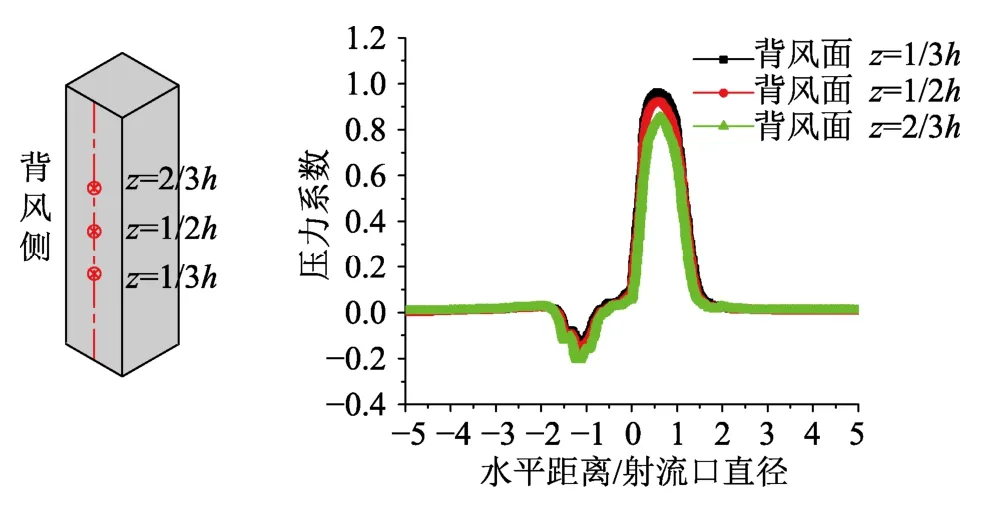
图25 建筑物背面监测点的压力系数时程曲线Fig.25 Pressure coefficient time history curves of the monitoring points on back of the building

2.2.3 建筑中心切面流场

建筑物中心切面流场如图26所示，下击暴流气流遭受到了建筑正面的阻碍，近乎垂直的气流方向变为竖直向上，并与建筑侧上方的气流聚集，随后在建筑正面与顶部分界处产生分离，建筑顶部受到吸力作用，而气流在建筑背面方向向下，并在背面发生再附形成涡。

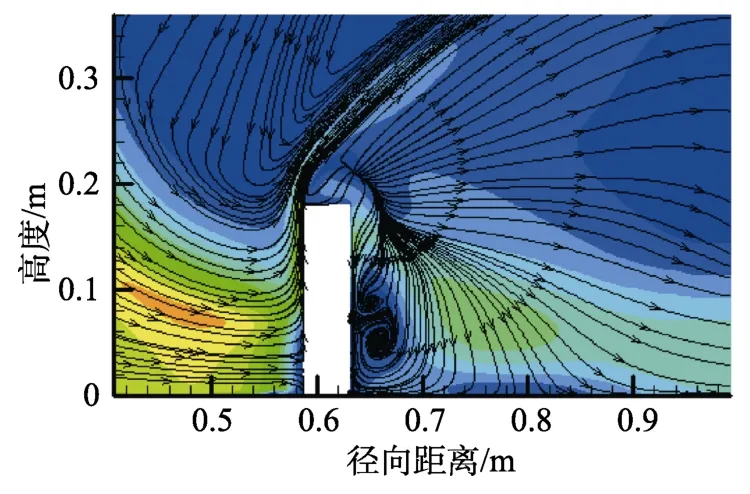
图26 建筑中心切面流场Fig.26 Flow field of building center cut surface

2.2.4 建筑表面压力系数

通过分析建筑物迎风面、背风面的压力系数云图，可以看出建筑在离射流口不同位置时，压力系数沿高度变化的不同。选取t=1s及t=2s为代表时刻，此时建筑表面压力系数云图见图27(a)、图27(b)。在下击暴流靠近的过程中，迎风面压力系数为正值，在近地面一段高度处保持不变，后随着高度的增加而减小，且中心线处的压力系数大于两侧的压力系数值。背面压力系数为负值，随着高度的增加先增大后减小。在下击暴流远离的过程情况则刚好相反。

图27 代表性时刻建筑物正面、背面压力系数云图Fig.27 Windward and leeward faces of building pressure coefficient contour at representative moments

2.2.5 局部压力系数

对建筑物局部压力系数进行模拟，测点布置同图9、图10。图28描述了移动型下击暴流与静止型下击暴流作用下建筑表面固定高度处压力系数对比情况，图29、图30描述了建筑物正面、背面中心线上压力系数对比情况。通过比较静止型及移动型下击暴流作用下建筑表面压力系数发现：两状态下建筑表面的压力系数变化趋势一致，但移动型下击暴流的压力系数大于静止型下击暴流压力系数，对建筑造成的作用更强，应在设计时加以考虑。

图28 建筑表面固定高度处压力系数对比Fig.28 Comparison of pressure coefficient at a fixed height of building surface

图29 建筑物正面中心线上压力系数对比Fig.29 Comparison of pressure coefficients on center line of front of building

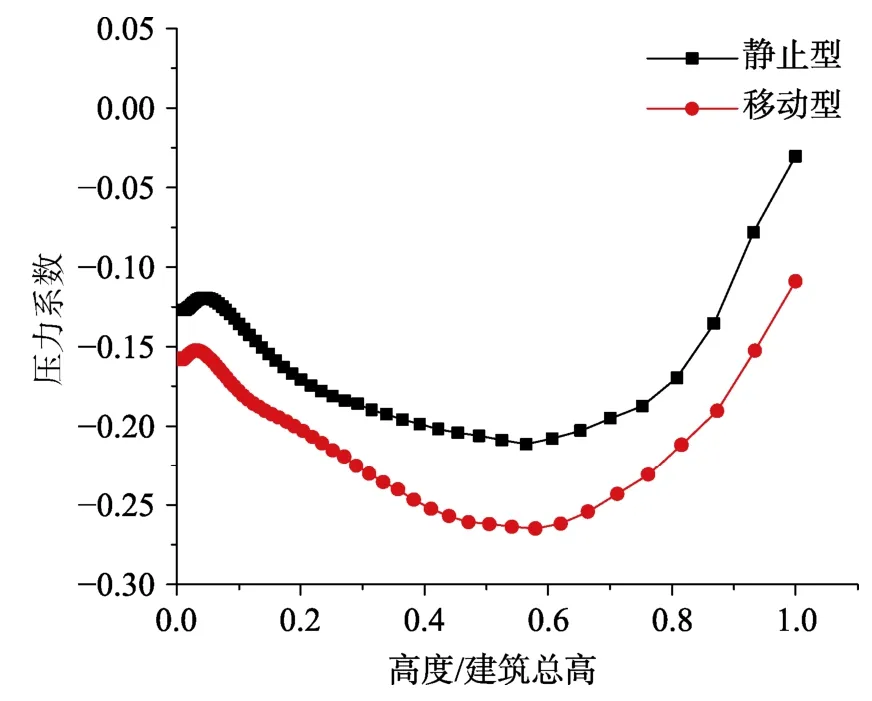
图30 建筑物背面中心线上压力系数对比Fig.30 Comparison of pressure coefficients on center line of back of building

本节基于数值模拟分析了移动下击暴流对建筑结构表面风压的影响，从本节可知下击暴流强风速区集中在近地面处，在建筑物迎风面底部会出现一段高压区，并给出了下击暴流移动的影响范围，在建筑结构设计中应着重注意。除了需要考虑下击暴流的建筑正面冲击，还应考虑射流中心经过后尾流区域涡旋的影响。中国风荷载规范只给出了边界层的风荷载，对于一些重要或体型特别的结构，由于下击暴流流场较为复杂，应通过风洞试验或数值模拟来确定结构风荷载和风致效应。