除尘器壳体双肢组合截面立柱轴压稳定性研究

宋碧颖，王登峰，王元清，方 滨

(1.江南大学环境与土木工程学院，无锡 214122；2.清华大学土木工程系，北京 100084；3.福建龙净环保股份有限公司，龙岩 364000)

除尘器是一种可有效减少废气中的颗粒污染物的通用环保装备。壳体内完成颗粒物收集捕捉工艺过程，是最重要的工艺部件。中大型除尘器壳体结构一般由带加劲肋的平直钢板墙板和H型钢立柱组成。墙板与立柱通过焊缝连接，形成密闭的除尘空间，并协同受载。壳体顶部设有支承横梁，用于悬挂阴极线、阳极板以及附着的积灰。这些荷载由顶部横梁传递到立柱，使得立柱直接承受轴向压力。由于放电距离方面的工艺要求以及承担较大荷载时的强度与稳定性设计方面的考虑，某些除尘器壳体顶部支承梁会设计为较宽的截面，因此，顶梁下方的壳体支承立柱也相应设计为较宽的截面。为了减少用钢量，此类立柱采用双肢H型钢组合截面，两肢间采用带角钢加劲肋的连接墙板连接。为了减小立柱长细比，提高其刚度，在壳体内部布置有垂直墙板的横向支撑，在相应高度位置，两肢H型钢柱间采用连接槽钢相连，支撑杆件通过与连接槽钢连接而间接形成对H型钢柱的垂直墙板方向约束。除尘器壳体结构如图1所示。

墙板作为蒙皮板件，能够为立柱承担部分荷载并约束其侧向变形，大大提高了立柱的稳定性[1]。关于蒙皮结构的受力性能，Nagy等[2]对门式刚架厂房中的蒙皮效应进行了研究，在保证安全的前提下对现有设计理论进行简化，并比较了不同压型板屋面板类型、檩条与屋面板的连接方式对其发挥蒙皮效应的影响。Wrzesien等[3－4]通过足尺试验研究了冷弯型钢门式刚架中的蒙皮效应，结果表明屋盖板的蒙皮效应可有效提高刚架在横向荷载作用下的承载能力，且屋盖板与刚架的节点形式对其有较大的影响；通过对建筑物进行以成本最小为目的优化设计，研究了受力蒙皮作用的影响，结果表明在投影平面上的跨度和柱距相同时，受力蒙皮板作用最大，此时内部框架的成本可以减少大约一半。Phan等[5]基于实验研究，在考虑受力蒙皮作用和刚架半刚性连接的前提下，应用遗传算法提出了一种冷弯型钢门式刚架的优化设计方法。

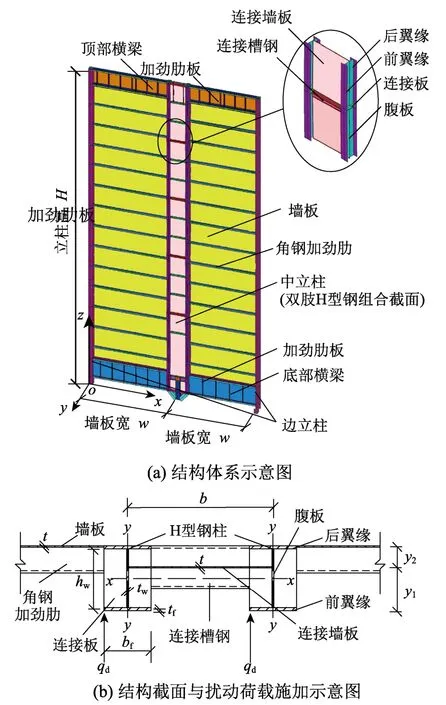
图1 除尘器壳体结构Fig.1 Structure of the electrostatic precipitator casing

国内研究方面，杨飞[6]对门式刚架轻型房屋钢结构中的蒙皮效应进行有限元研究，结果表明蒙皮效应提高了结构的抗侧刚度以及承载能力，但使振型变得复杂。左洋等[7]在理论分析的基础上，利用试验与有限元方法，研究了开洞集装箱房屋的纵向刚度，分析了开洞面积、洞口高宽比的影响规律，并提出设计建议。潘立程等[8]针对除尘器的蒙皮结构壳体墙板，利用有限元方法，研究了其在均匀竖向压力作用下的破坏形式与承载能力，并分析了墙板构造对其承载能力的影响。陈天乐[9]采用有限元方法对比分析了有无考虑蒙皮效应的轻钢结构受力性能，发现考虑蒙皮效应后，可以减小构件截面尺寸以及减少横向约束，具有更好的经济性。钱海峰等[10]利用理论分析与有限元方法，对除尘器壳体墙板-立柱结构体系在墙板直接承受横向荷载作用下的荷载分配进行了研究，并考虑墙板的蒙皮作用作用，提出了一种除尘器壳体立柱内力计算方法。

目前对蒙皮结构的研究主要集中于以压型钢板为蒙皮板的轻钢结构，本文研究的除尘器围护体系中双肢组合截面立柱在构造上有其特殊性，需要考虑加劲墙板蒙皮作用，已有的研究结论并不完全适合指导其结构设计。本文考虑结构体系的初始几何缺陷以及立柱轧制、墙板与立柱焊接过程中产生的残余应力影响，通过大量非线性有限元分析，明确双肢组合截面柱在轴向压力下的破坏机理，研究多种构造参数的影响规律，提出了立柱稳定承载力计算建议。本文的研究一是直接解决了除尘器壳体中常用的大截面骨架立柱在考虑墙板作用时的轴压稳定性计算问题，使得除尘器壳体支承构件的设计能够可靠且经济；二是为受加劲蒙皮板连续支撑的H形截面构件的稳定性设计提供参考，分析了此类结构稳定性的主要影响因素，具有一定的理论意义和工程应用价值。

1 分析模型

1.1 结构模型

依据实际中常规的除尘器壳体结构几何参数，设计了10例基础研究模型，几何参数如表1所示。这些模型涵盖了大型、中型、小型除尘器的几何尺寸，确保研究结果具有普遍性。实际除尘器一般布置有多跨围护墙板，以保证收尘效果。为简化模型，提高计算效率，仅取两跨墙板建模。中间双肢组合柱截面如图1(b)所示。H型钢柱与墙板直接相连的一侧翼缘称为后翼缘，不受墙板约束的立柱翼缘称为前翼缘。连接墙板与两肢立柱的腹板通过焊接连接。立柱总高度H，横向支撑间距l0(即连接槽钢间距，亦为单肢立柱绕y轴的计算长度)，壳体墙板宽度w，连接墙板宽度b，墙板与连接墙板壁厚t，连接墙板中心与后翼缘距离y2。

1.2 有限元计算模型

采用ANSYS有限元程序进行数值分析，选用Shell181单元对所有结构构件进行模拟。材料参数如表2所示。钢材本构采用双线性等向强化模型，以米赛斯准则判断是否发生屈服。考虑几何非线性影响，采用弧长法跟踪结构响应路径。

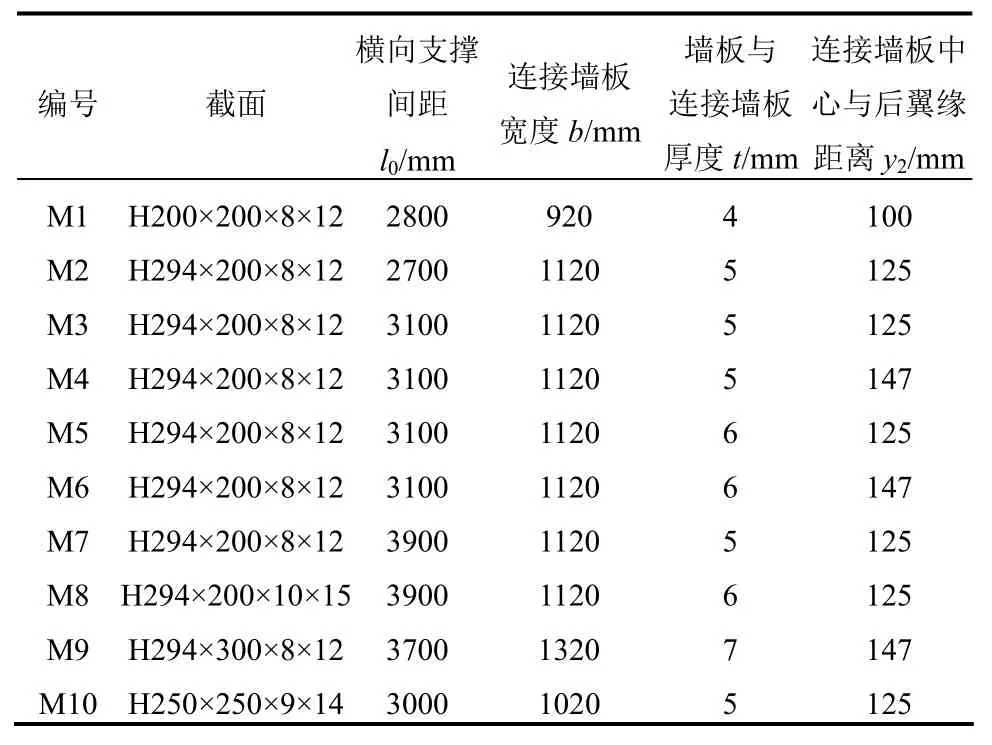
表1 计算模型几何参数Table 1 Geometrical parameters of computational models

表2 结构材料参数Table 2 Material parameters of the structure

根据实际情况，对有限元模型施加约束与荷载。对于壳体墙板，在顶部与底部施加垂直于墙板方向的平动约束(y向)，模拟大刚度加劲顶板、灰斗加劲壁板的约束。对于壳体立柱，在两肢间连接槽钢中点位置施加垂直墙板方向的平动约束(y向)，模拟等间距布置横向支撑的约束；在中柱底部施加3个方向的平动约束；在两侧边柱底部仅施加垂直于墙板方向和高度方向的平动约束(y和z向)，以释放高温烟气产生的墙板平面内温度变形；在中间组合柱顶设置一块刚性盖板，便于施加竖向均布荷载。

1.3 有限元分析方法验证

为验证本文中有限元建模、加载和求解方法的准确性，对文献[11]中双向加劲钢板在轴向和横向荷载共同作用下破坏性加载试验进行非线性有限元模拟。根据文献中记载的试验模型几何尺寸和约束情况建立有限元验证模型，钢材材性采用论文中给出的实测数据的平均值。加载试验中轴向荷载加载速率较快，并较早达到预定值，横向荷载加载速率较慢，最后破坏是在横向荷载作用阶段。因此，按照实际试验加载过程，有限元模拟中首先施加轴向荷载，其次施加横向荷载至破坏。本文模拟得到的极限承载力与文献中试验结果对比如表3所示；两个典型模型加劲板中心结点荷载-位移曲线的有限元模拟情况与试验记录情况对比分别如图2(a)和图2(b)所示。可见，有限元模拟结果与试验结果在极限承载力与荷载-位移响应路径方面吻合良好，本文有限元模型构建方法与非线性分析技术基本可靠，能满足后续结构体系承载性能研究的要求。

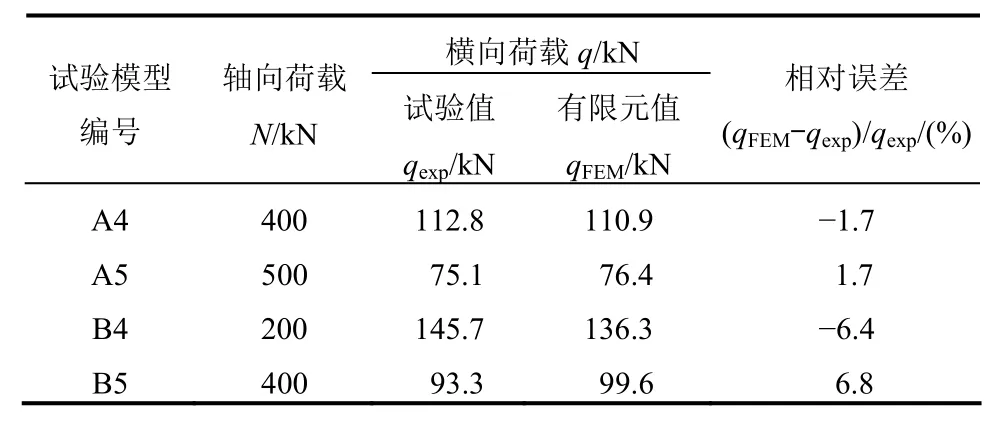
表3 本文有限元结果与文献试验结果对比Table 3 Comparison of results between finite element method and tests

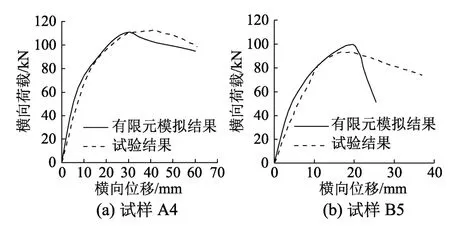
图2 荷载-位移曲线的有限元模拟情况与试验记录情况对比Fig.2 Comparison of the load-displacement curves between finite element simulations and test records

1.4 初始几何缺陷

文献[12]中对除尘器壳体结构体系中单肢H型钢柱轴压稳定性的敏感初始几何缺陷进行了研究，结果表明，柱顶区域前半截面(前翼缘与前腹板)的弯扭变形对单肢H型钢柱稳定性是最不利的。这是因为墙板作为蒙皮结构，能够为立柱承担荷载，导致仅在靠近柱顶的局部区域存在高压应力；且墙板的存在增大了后翼缘受载面积，使得其荷载水平低于前翼缘；前翼缘相对较自由，容易发生变形。双肢柱的内力分布、变形约束与单肢H型钢柱类似，因此这种最不利初始缺陷同样适用于本文的双肢组合截面柱。

基于这样的推断，建模时首先对中间两肢H型钢柱在各连接槽钢区间(连接槽钢可视作H型钢柱的侧向支撑)构造了绕y轴的正弦半波形式初始几何缺陷，形成初始弯曲变形，缺陷形式如图3所示。缺陷幅值δ取千分之一柱高。

为了引入前半部分截面的初始扭转变形，并考虑墙板及连接墙板上初始几何缺陷的影响，对仅有立柱正弦半波整体缺陷的结构模型施加柱顶轴力进行非线性计算，同时对立柱一侧翼缘施加均布扰动线荷载qd。扰动荷载作用范围为立柱上轴压应力由σz,max(最大轴压应力)衰减到0.85σz,max的区间，扰动荷载合力值取柱顶轴向荷载的千分之一，扰动荷载的施加如图1(b)所示。达到荷载极值点时结构上较大的变形为连接墙板靠近柱顶区域和中上部墙板邻近立柱区域的y向变形，立柱的变形幅值与之相比不超过15%。将此模型达到极值点时的变形模态作为结构极值点变形缺陷模态，幅值取千分之一柱高。后续分析均引入这种几何缺陷模态。这样的缺陷模型既包括了立柱在高压应力区易于变形的前半部分截面初始弯扭变形，又包括了墙板和连接墙板上的局部凹凸变形，充分考虑了最不利初始几何缺陷的影响。

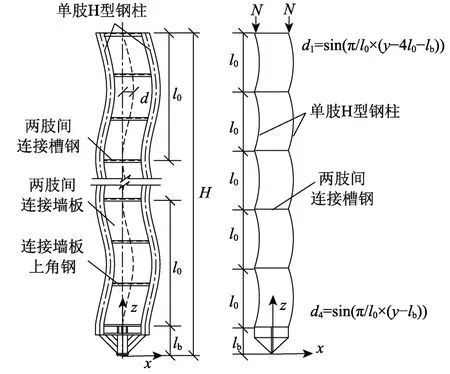
图3 初始弯曲缺陷形式Fig.3 Initial bending imperfection shape of the column

1.5 焊接残余应力的影响

结构体系中残余应力的形成源于3个步骤：一是H型钢的轧制过程；二是H型钢腹板与连接墙板的焊接过程；三是H型钢后翼缘与墙板的焊接过程。残余应力的存在会影响立柱的稳定性。本文通过有限元方法，利用瞬态移动热源和生死单元技术模拟焊接过程中的温度场变化，通过热力耦合将瞬时温度作为外荷载施加到实体结构上，形成应力场。对于热轧H型钢的轧制残余应力，我国钢结构规范采用图4(a)的模式[13]。因此模拟轧制过程时，控制H型钢各板件残余拉、压应力幅值为0.3fy，即70.5MPa左右。钢材高温下力学材料性能(弹性模量E与屈服强度fy折减系数)、热学材料性能(导热系数λ、热膨胀系数α、比热容C)均按照《建筑钢结构防火技术规范》[14]取值。为简化计算，忽略辐射的影响，仅考虑对流换热。换热系数取15W·m-2·℃-1。以模型M5为例，考虑对称性，左肢H型钢最终形成的轴向残余应力分布如图4(b)所示。图4(b)表明，H型钢腹板与连接墙板连接处、H型钢后翼缘与墙板连接处由于焊接过程中温度较高冷却较慢而产生较大的残余拉应力，其中，后翼缘与墙板连接处由于焊接次序最末，产生的残余拉应力最大，可达屈服强度fy。残余拉应力自焊接部位向外衰减较快。H型钢前翼缘最终残余应力分布情况受轧制的影响较大，前翼缘与腹板连接处产生残余拉应力，其余部位产生残余压应力。焊接过程增大了前翼缘的残余压应力，但改变幅度很小，不超过0.03fy。

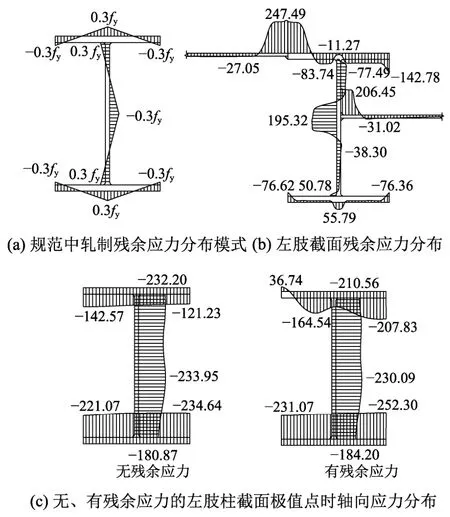
图4 残余应力与荷载极值时轴向应力分布图 /MPaFig.4 Distributions of residual stress and axial stress at load extremes

为考察残余应力对立柱轴压承载能力的定量影响，将利用实体单元进行轧制与焊接过程模拟形成的残余应力分布简化后引入壳单元构建的结构体系有限元模型进行非线性计算，计算结构在有、无残余应力时的稳定承载力。对于不同构造与尺寸的模型M1和M5，考虑残余应力后的稳定承载力分别为未考虑残余应力的0.971倍与0.989倍，减小幅度均不超过5%。同一截面上，无、有残余应力情况左肢立柱截面达到极限承载力时的轴向应力分布如图4(c)所示。立柱的失稳主要体现为前半部分截面的失稳，在无残余应力情况荷载达到极值时，腹板与前翼缘组成截面的压应力分布较为均匀，基本接近全截面屈服的水平。残余压应力的存在可能会透支一定前半部分截面应力增加空间，但图4(b)表明，多步加工使得前腹板与前翼缘上的残余拉、压应力分布基本平衡，残余应力引起初始轴向内力合量不超过该部分截面屈服荷载的5%。图4(c)表明，有、无残余应力情况最终发生破坏时的立柱截面轴向应力分布差异不大，有残余应力时前翼缘的压应力水平更高一些。在有、无残余应力时，分别对H型钢前半部分截面轴向加载阶段计算应力增量积分(即前半部分截面的轴向内力加载量)，继而求出比值，M1模型有、无残余应力情况轴力增量比值为0.983，M5模型有、无残余应力情况轴力增量比值为0.982。可见，由于易于发生失稳的H型钢前半部分截面残余应力基本平衡，且达到极限承载力时截面处在一个较为均匀的高压应力水平，因此残余应力的影响不大。考虑到由于残余应力的存在立柱承载力减小幅度不超过5%，且这种影响对于不同构造立柱差异不大，因此，为简化计算，后续有限元模型中不再引入残余应力，而用一个偏于安全的折减系数来反映残余应力的不利影响。

2 双肢组合截面柱在轴压作用下加载响应分析

2.1 柱顶略下方的失稳模态

以模型M5的立柱为例分析其失稳过程。H型钢柱后翼缘受到墙板约束，其腹板受到连接墙板约束，因此后翼缘和腹板的x向变形发展很小，立柱难以呈现绕y轴的整体弯曲失稳。尽管墙板上的角钢通过连接板对前翼缘提供侧向支撑，同时约束前半部分截面的扭转变形(如图1所示)，但这种支撑是离散的，且无墙板分担前翼缘所受荷载，前翼缘压应力水平较高，加之初始几何缺陷的存在，易于发生扭转，并带动前半部分腹板局部弯曲，导致前半部分T形截面形成一定的侧向弯扭，其截面变形如图5(a)所示，图中粗实线为变形后截面，细虚线为初始截面。由于立柱前、后部分截面变形差异，失稳后发生翘曲，不再保持平直截面以及H形的刚性周边。本例立柱的失稳发生在柱顶略下方，此处离加载点很近，立柱截面应力水平很高。因此，H型钢柱的失稳可以归纳为，弹塑性阶段柱顶略下方局部区域的相关失稳。失稳模态如图5(b)所示。

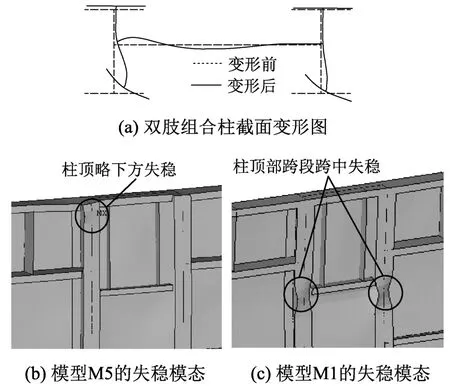
图5 立柱的两种典型失稳模态Fig.5 Two typical buckling modes of the column

2.2 柱顶部跨段跨中的失稳模态

除了上例结构的失稳模态外，当墙板壁厚较薄，墙板蒙皮作用较小，且立柱本身抗弯、抗扭刚度较小时，立柱会在顶部第1跨段跨中出现相关失稳，如图5(c)所示。随着轴向荷载由柱顶向下传递，H型钢柱承担的荷载比例逐渐减小，墙板承担的荷载比例逐渐增大，跨中区域立柱承担的轴力比柱顶区域小。失稳发生在轴力小的区域，是因为立柱在跨中远离连接板，所受约束较弱，跨中区段抵抗失稳刚度不足所致。在柱顶跨段以下的其它跨段，立柱承担的轴向力更小，而所受约束及自身刚度没有减小，因此本文研究的所有几何参数的结构，其立柱失稳均发生在柱顶跨段。

3 壳体立柱轴压稳定性影响因素分析

本文取稳定系数φ来衡量壳体立柱的轴压稳定性，φ按下式计算：

式中，AH为单肢H型钢柱截面积。

由于实际工程中，柱顶施加的轴向压力通过刚性盖板直接分配一部分到墙板与连接墙板，实际承担轴向荷载的是墙板与H型钢柱组成的组合体系，其承载面积必定超过2AH。因此名义上，柱顶施加的极限荷载Ncr完全可能大于两肢H型钢全截面屈服荷载Ny，即φ值存在大于1的情况。

3.1 连接墙板与H型钢柱腹板连接位置的影响

壳体立柱两肢间连接墙板与H型钢柱腹板的连接位置如图1(b)所示。连接墙板中心与前翼缘距离为y1，与后翼缘距离为y2。在工程设计中，因为工艺要求和一些通用件的尺寸要求，除尘器壳体立柱两肢间连接墙板并不全都布置在H型钢截面对称轴上(图1(b)中x―x轴)。本文选取了两个基础计算模型M5和M6，两者除连接墙板位置不同外，其余参数都相同，以考察连接墙板位置对立柱稳定性的影响。其中M5的y2取125 mm(偏近后翼缘)，M6的y2取147 mm(位于对称轴)。设计了两组计算模型M5-t、M6-t。以M5-t为例说明其编号规则：即模型组基本参数同M5，仅改变墙板与连接墙板壁厚t而保持其余构造参数不变。不同墙板厚度情况下，y2分别取147 mm和125 mm时的φ值比较如图6所示。y2=147 mm时的φ值明显大于y2=125 mm时的，说明连接墙板越靠近前翼缘，立柱稳定性越好，而且墙板越厚，差异越大。分析其原因在于，立柱的失稳源于前翼缘，连接墙板因为靠近前翼缘，对易于失稳的前半部分截面约束更加直接有效。当连接墙板远离前翼缘时(y2减小)，截面上不受约束的悬伸段(腹板上y1区段与前翼缘组成的T形截面)加大，前翼缘所受约束变弱，腹板也更易于发生局部弯曲，立柱稳定性变差。在连接墙板壁厚较大时，连接墙板的约束作用更大，这种情况下连接墙板所处位置的影响也更大。

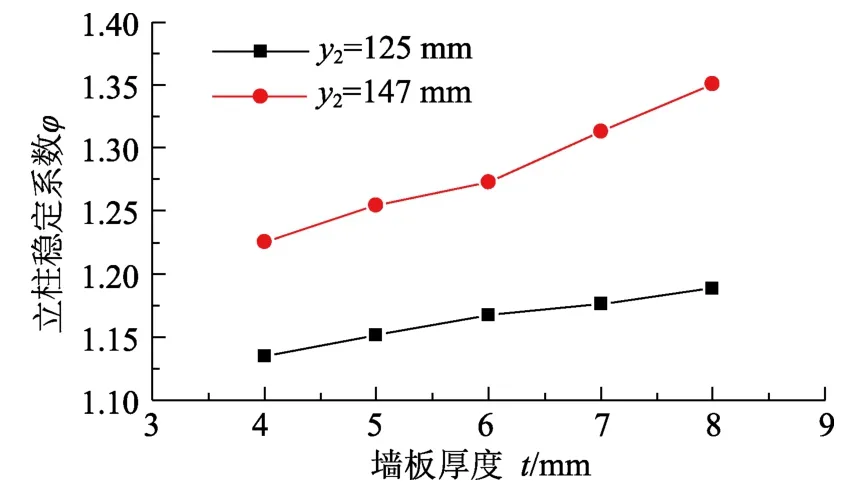
图6 不同连接墙板位置时的立柱稳定性比较(M5、M6)Fig.6 Comparison of buckling factors between different connecting wallboard positions (M5、M6)

3.2 墙板角钢加劲肋及连接板的影响

墙板角钢加劲肋一是增强墙板，更好发挥其受力蒙皮作用；二是通过连接板对立柱提供侧向支撑，但是不能取角钢间距作为立柱绕y轴的计算长度，原因在于：1) 角钢是为了减小墙板区格而设置，其截面刚度远小于两肢间连接槽钢，而跨度(等于墙板宽度)远大于连接槽钢，对H型钢柱的约束作用较弱；2) 初始几何缺陷使得角钢在加载过程中容易发生变形，难以保持挺直撑杆的作用，其支撑刚度进一步受到削弱；3) 立柱失稳发生在前翼缘，而墙板角钢加劲肋通过连接板对前翼缘起到一定的支撑作用，但是角钢加劲肋支撑力的中心线更靠近后翼缘，这对H型钢截面反而作用了一个不利扭矩[15]。计算结果表明，H型钢柱侧边与连接板连接结点(即角钢支撑位置)的x向变形约为立柱上最大x向变形值的30%～50%，显著大于H型钢与两肢间连接槽钢连接位置的x向变形(不超过最大x向变形值的15%)，因此，不取角钢加劲肋间距作为立柱的计算长度，而取两肢间连接槽钢间距作为立柱的计算长度。

在模型M4和M8的基础上，取不同角钢加劲肋截面，得到模型组M4-A∟和M8-A∟。不同墙板角钢加劲肋时，立柱的荷载-位移曲线如图7所示。图7(a)对应的立柱计算长度较小(l0=3100 mm)，立柱长细比较小，采用不同角钢加劲肋截面时的荷载-位移曲线在达到Ncr前基本重合，Ncr值相差不超过2.3%，无连接板时的Ncr值比有连接板时的小0.1%。图7(b)对应的立柱计算长度较大(l0=3900 mm)，立柱长细比较大，不同角钢加劲肋截面时的Ncr值差异比l0=3100 mm 时的略大些，但不超过3.0%；无连接板时的Ncr值比有连接板时的小1.3%。说明立柱长细比大时，墙板角钢加劲肋的支撑作用相对更加明显，由于墙板加劲肋增强，对墙板受力蒙皮作用的有利影响增加，连接板的作用也更加明显。上述计算分析表明，墙板角钢加劲肋对立柱的侧向支撑作用是有限的，其截面刚度对立柱稳定性影响较小，对立柱起到主要约束作用的是墙板和连接墙板。连接板刚度对于立柱稳定性影响很小，主要是因为：1) 立柱失稳发生在相邻连接板之间区域，连接板的增强对于限制立柱变形没有直接作用；2) 连接板与墙板角钢加劲肋连接，由于初始几何缺陷以及加载过程中的变形发展，角钢加劲肋会带动连接板发生扭转变形，削弱连接板对于立柱的扭转约束；3) 对于立柱截面变形的限制主要来自墙板和连接墙板，而非连接板。

3.3 墙板和连接墙板壁厚t的影响

除尘器壳体设计时，墙板和连接墙板为等壁厚，本文分析时也取墙板和连接墙板壁厚相等，为t。不同H型钢截面和计算长度时，立柱稳定系数φ与墙板壁厚t的关系曲线如图8所示。φ值随着t值的增大而增大。当墙板和连接墙板壁厚增大时，其对立柱的侧向支撑增强，同时所能分担的轴向荷载的比重以及绝对量值均有增大，立柱的稳定性自然得以增强。

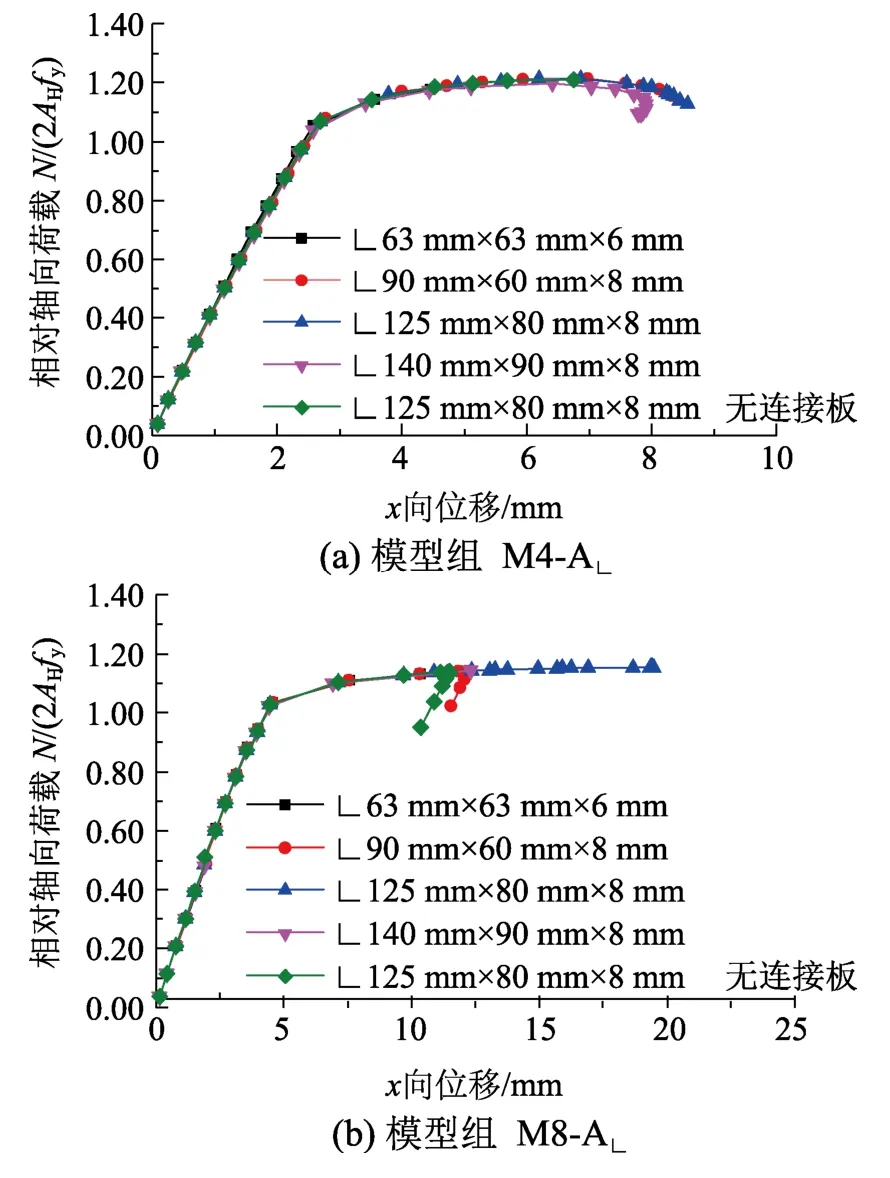
图7 不同墙板角钢加劲肋时的立柱荷载-位移曲线比较Fig.7 Comparison among the load-displacement curves for different sizes of angle stiffeners on wallboard

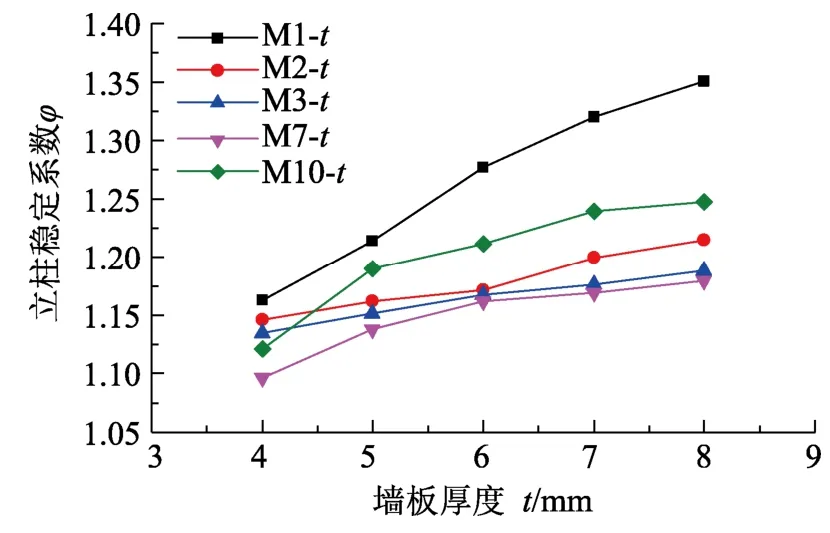
图8 φ与t的关系曲线Fig.8 Relationship curves between φ and t

3.4 连接墙板宽度b的影响

为了研究两肢间连接墙板宽度对立柱稳定性的影响，在模型M5的基础上，改变连接墙板宽度b后进行非线性计算。连接墙板宽度b分别取920 mm、1120 mm和1320 mm时的荷载-位移曲线如图9所示，3条曲线几乎完全重合，彼此极限荷载Ncr值相差不超过0.2%，表明连接墙板宽度对立柱稳定性影响很小，这也说明在连接墙板壁厚一定时，连接墙板宽厚比对立柱稳定性影响很小。

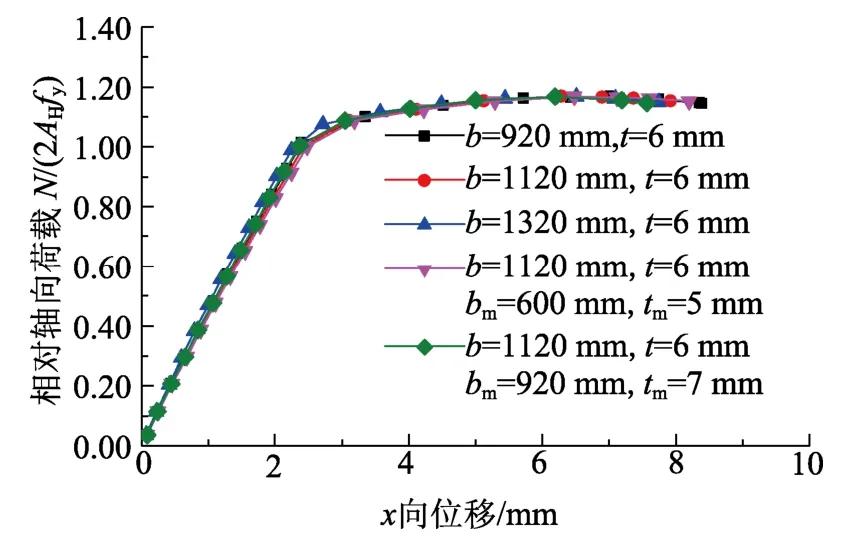
图9 不同连接墙板宽厚比时的荷载-位移曲线Fig.9 Load-displacement curves for different b/t

保持b=1120 mm，其它参数不变，仅改变连接墙板中间区域的壁厚，中间变壁厚区域宽度为bm，其壁厚为tm，与两肢H型钢相邻区域的连接墙板壁厚仍为t=6 mm。当bm=600 mm，tm=5 mm和bm=920 mm，tm=7 mm时的荷载-位移曲线亦如图9所示，与整个连接墙板取等厚度t=6 mm时的曲线几乎完全重合，彼此Ncr值相差不超过0.03%。这表明连接墙板对立柱稳定性有影响的只是与立柱相邻的两边各0.09b部分，中间区域连接墙板对立柱稳定性影响很小。除尘器壳体连接墙板宽厚比b/t一般超过150，由于初始几何缺陷的存在，连接墙板在加载初期就会发生局部屈曲，在此宽厚比值基础上稍作增减，对连接墙板刚度影响不大，局部屈曲依然很早发生，因此连接墙板中间区域在加载过程中发挥的作用很小。连接墙板上与立柱相邻部分对立柱承载有贡献，这部分的壁厚会影响立柱稳定性。由此可以推断，在柱顶轴力作用时，两肢间连接墙板中间0.8b部分的壁厚是有优化空间的。此外，由于墙板直接约束后翼缘，对于易于失稳的前半部分截面没有直接约束作用，且墙板宽厚比远大于连接墙板宽厚比，因此可以推断，改变墙板宽度对于双肢柱轴压稳定性影响不大。

3.5 H型钢柱翼缘宽厚比bf/tf的影响

为了考察H型钢截面翼缘宽厚比bf/tf对立柱稳定性的影响，在模型M5、M9、M10的基础上，保持H型钢截面翼缘宽度bf不变，腹板几何尺寸与其它参数均不变，仅改变翼缘壁厚tf值，由此改变bf/tf值，得到3组计算模型M5-bf/tf、M9-bf/tf、M10-bf/tf。立柱稳定系数φ与H型钢翼缘宽厚比bf/tf的关系曲线如图10所示。事实上，bf/tf值改变会引起立柱绕y轴长细比λHy小量改变，观察图8中数据，模型组M2-t、M3-t、M7-t的l0由2700 mm增加到3900 mm，λHy增长了44%，但φ值减小不超过5%。本文算例中bf/tf值改变引起的λHy变化不超过11%，对φ值的影响更小，可以忽略。对于图10中所示关系曲线，可以认为φ值的变化完全由bf/tf值变化引起。

由图10可见，关系曲线并非单调发展，φ值随着bf/tf值的增大先增后降。立柱的失稳包括前半部分截面整体失稳与板件局部失稳。bf/tf值越大，前半部分截面的抗扭长细比越大；此外，bf/tf值越大，翼缘对于腹板的嵌固作用是减弱的，在腹板高厚比不变的情况下，前半部分截面更易变形，这些对其稳定性是不利的。有利的方面是，墙板对立柱的侧向约束通过墙板对后翼缘的作用实现，bf/tf值越大，后翼缘越柔，立柱截面刚度减小，墙板分担的轴向荷载比例增大，且墙板对后翼缘的相对约束作用越强，稳定系数会提高。结合上述因素，翼缘宽厚比对立柱稳定性的影响不是单调的。

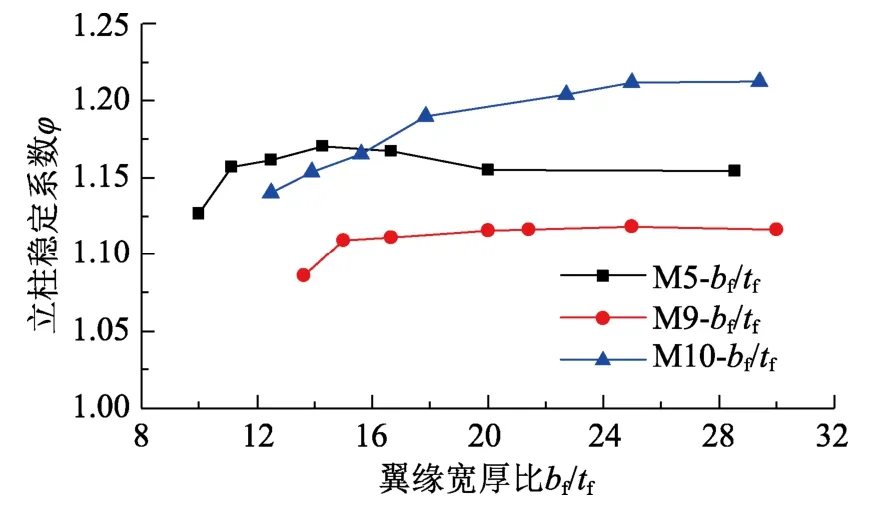
图10 φ与bf/tf的关系曲线Fig.10 Relationship curves between φ and bf/tf

3.6 H型钢柱腹板高厚比hw/tw的影响

保持立柱上其它几何参数不变，通过改变截面参数hw、tw以及计算长度l0，保持λHy、bf/tf不变，而仅改变hw/tw值。φ与hw/tw的关系曲线如图11所示。图11表明，随着hw/tw的增加，φ值基本呈现减小趋势。一方面，腹板高厚比增大，在初始缺陷的诱发下腹板更易于发生局部弯曲，继而带动前半部分截面弯扭变形；另一方面，腹板高厚比的增大，减弱了腹板对于翼缘的约束作用，前翼缘更易发生扭转变形，这对立柱稳定性也不利。

3.7 H型钢柱长细比λHy的影响

保持立柱截面及墙板几何尺寸不变，通过改变计算长度l0改变λHy值，设计了4组计算模型M1-λHy、M3-λHy、M5-λHy和M8-λHy。立柱稳定系数φ与H型钢柱长细比λHy的关系曲线如图12所示。图12表明，φ值随着λHy增加而非线性减小。说明随着H型钢柱长细比λHy增大，立柱稳定性减弱。由于立柱的失稳源于压应力较大的前翼缘，由其弯扭变形引起，当H型钢柱长细比λHy增大时，立柱前半部分T形截面整体抵抗弯扭刚度减小，更易于发生弯扭变形，造成立柱稳定系数降低。

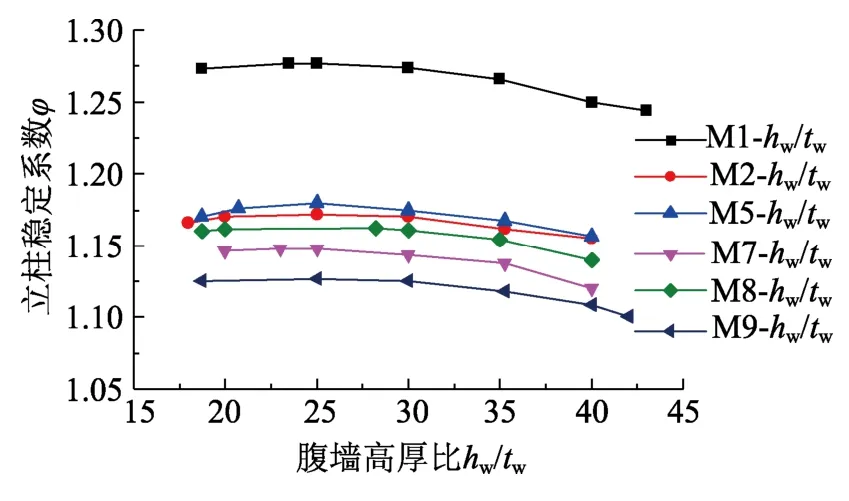
图11 φ与hw/tw的关系曲线Fig.11 Relationship curves between φ and hw/tw

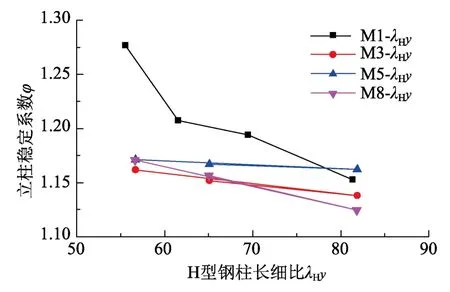
图12 φ与λHy的关系曲线Fig.12 Relationship curves between φ and λHy

4 除尘器壳体双肢组合截面立柱轴压稳定承载力计算建议

本文通过对大量除尘器壳体墙板-立柱结构体系有限元模型的非线性计算，得到了不同几何参数下的双肢组合截面轴心受压柱的稳定承载力计算值。各几何参数的考察范围均基于实际除尘器结构，墙板及连接墙板壁厚t为4 mm～8 mm；H型钢柱长细比λHy为44～89，翼缘宽厚比bf/tf为10～30，腹板高厚比hw/tw为18.8～43。通过对大量计算数据基于最小二乘法的回归分析，壳体双肢组合截面柱轴压下的稳定系数φ可按式(2)计算。由于计算时未考虑残余应力的不利影响，因此，提出φ值计算式时统一引入一个折减系数0.95。

由式(2)得到的拟合值与有限元计算值平均相对误差2.3%，最大相对误差7.2%，该拟合式基本是准确可靠的。

考虑立柱达到稳定承载力时，柱顶区域腹板有严重的塑性开展，且部分结构变形会超过l0/500，因此，提出立柱轴压稳定承载力设计值Nr时，考虑一个安全储备系数0.95，同时可控制在轴力作用下结构的变形满足正常使用要求，Nr按下式计算：

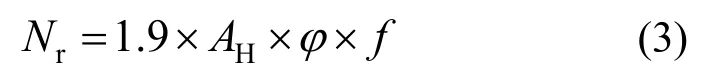
式中，f为钢材强度设计值。

5 结论

本文基于实际工程中除尘器壳体的几何构造，充分考虑结构初始缺陷的影响，对双肢组合截面轴心受压柱的稳定性进行了大量非线性有限元分析，得到了如下结论：

(1) H型钢柱在轧制、与连接墙板和墙板间的焊接过程产生的残余应力会小幅降低立柱稳定承载力。

(2) 立柱的失稳均发生在柱顶跨段内，失稳形式为前翼缘与前腹板组成前半部分T形截面整体弯扭失稳与腹板局部失稳同时发生的相关失稳；失稳高度位置可能在柱顶略下方区域，或是跨中区域；立柱达到稳定承载力时，柱顶区域都有较为严重的塑性开展。

(3) 墙板参数分析表明连接墙板越靠近前翼缘，立柱的稳定系数越高；墙板角钢加劲肋和连接板对立柱稳定性影响较小，增强它们的刚度对立柱稳定系数提高很有限；立柱稳定系数随着墙板和连接墙板壁厚增大而增大；连接墙板宽度对立柱稳定性影响较小，增大连接墙板与立柱相邻区域壁厚可以有效提高立柱稳定系数，增大连接墙板中间区域壁厚对立柱稳定系数影响较小。

(4) H型钢立柱参数分析表明立柱稳定系数不随H型钢柱翼缘宽厚比单调变化；而随H型钢柱绕弱轴的长细比和腹板高厚比的增大而减小。

(5) 基于大量非线性有限元计算结果，提出了除尘器壳体双肢组合截面轴心受压柱稳定承载力设计值的计算建议。