基于蒙特卡洛法的绿篱修剪机工作空间分析
2020-03-16张新阳
张新阳,陈 玉
(安徽工程大学 机械工程学院,安徽 芜湖 241000)
随着城市绿化面积不断扩大,加之人们追求绿色舒适生活环境,绿篱作为城市生活的点缀,起到美化环境、净化空气、防尘降噪、隔离视线等作用。而绿篱植物是季节性生长植物,若肆意生长不仅影响道路交通安全,而且影响美观度,所以需要定期进行修剪维护,而人工修剪有费时费力、工作效率低等缺点,因而车载式绿篱机成为当下国内外对于城市道路交通绿化的不二之选。针对这种情况,设计了满足修剪一定曲面造型的回转型绿篱修剪机的主要结构参数,并利用MATLAB机器人工具箱对其末端修剪刀具的运动学问题进行计算及工作空间分析仿真。
1 回转型绿篱修剪机设计
1.1 结构方案模型
回转型绿篱修剪机结构主体设计[1]部分由3个转动关节和3个移动关节六自由度组成,其主体结构组成部分如图1所示。

图1 回转型绿篱机主体结构示意图
各主要模块的组成及功能实现如下:①回转平台。主要由回转支承、齿轮驱动等装置组成。当进行修剪任务时,转动绿篱机到达所要修剪绿篱植物的所在方位;当进行转场修剪时,各机构完成修剪任务,收回到移动底盘车内,不妨碍道路车辆正常行驶。②升降装置。主要由丝杆、电机驱动、丝杆滑块等装置组成,主要作用是对绿篱植物自上而下修剪时进行高度的调节。③伸缩机构。机构组成包括外内臂、伸缩电机等。研究设计由两组伸缩臂机构组成,分别有着不同的作用,顶层伸缩臂起到定位作用,将末端修剪装置定位到待修剪绿篱轴心等位置;底层伸缩臂作用是在修剪一定几何曲面绿篱时,调节绿篱半径大小。④角度调节机构。通过活动关节与伸缩竖直臂连接,当修剪具有一定曲面造型时可在一定角度范围内通过关节的摆动实现。
1.2 技术指标
根据市场调研、市场需求及查阅城市道路绿化景观设计标准确定技术指标:
(1)采用电动驱动。
(2)修剪可变直径大小的球形、锥形等复杂曲面绿篱(直径范围在600~1 200 mm),以及常规平面、侧面绿篱。研究以修剪球形作为此次研究目标。
(3)绿篱修剪刀具高度可调。
(4)绿篱修剪机末端修剪刀具可在水平和竖直方向上进行调节。
(5)采用电动底盘车作为移动平台,绿篱机及支架放置在平台上。
1.3 绿篱修剪机各机构尺寸
根据所确定的技术指标和绿篱修剪机各组成部分的功能,需要对绿篱修剪机各关节的作用范围尺寸进行设计,具体尺寸如图2所示。这不仅是绿篱修剪机结构设计的一个重要组成部分,也为接下来结构仿真分析做准备。

图2 回转型绿篱修剪机各机构尺寸示意图
(1)确定绿篱修剪对象尺寸。考虑到修剪末端承受载荷情况和技术要求,所设计回转型绿篱修剪机的修剪绿篱直径范围为D=600~1 200 mm,由于绿篱植物底部0.2~0.3 m的高度缺少阳光照射、枝叶稀薄,不需要进行修剪,取球形绿篱的最大高度为1 000 mm,满足城市及园林绿化规定标准。
(2)确定升降装置基本行程。当末端刀具要进行圆球绿篱顶部的修剪时,则600 mm≤H1+H2-H3≤1 000 mm。其中,H1为承载车厢底至地面的高度,设为固定值800 mm。当修剪绿篱最底部位置时,升降装置下降到最低极限位置,防止底层伸缩臂与顶层伸缩臂发生干涉碰撞。顶层伸缩臂末端与底层伸缩臂之间由旋转电机通过旋转轴连接,取其中间连接距离为150 mm,则H3=1 000+150=1 150 mm,所以H2=1 000-H1+H3=1 400 mm,即升降装置的基本行程确定为1 400 mm。当进行绿篱修剪时,升降装置只需下降1 000 mm,即可满足修剪要求,因此确定绿篱修剪机升降装置的移动范围是400 mm≤H2≤1 400 mm。
(3)确定伸缩臂的基本行程。根据绿篱修剪机的修剪技术指标,确定底层伸缩臂的范围为0≤L4≤600 mm,即为圆球绿篱的半径范围。取底层伸缩内臂的基本行程为600 mm,由于伸缩机构完全伸出后,伸缩机构的内臂与外臂有一段重叠的距离,取交错的长度为150 mm,则底层伸缩内臂的长度为L4=600+150=750 mm。顶层伸缩臂主要目的是使得固定在伸缩大臂机构上的旋转装置的旋转轴心移动到球形绿篱的球心位置上,由于承载车宽为L6=1 400 mm,承载车靠近绿篱植物一侧的路缘石距离为L5=350 mm,确定伸缩大臂机构的基本行程L2=1 500 mm。
2 回转型绿篱修剪机运动学分析
回转型绿篱修剪机是由刚性杆件通过转动关节或移动关节串联组成的开式机构,通过各个机构之间的相对运动,使绿篱修剪末端修剪刀具在机械臂的伸缩以及升降装置等作用下到达不同的空间位姿,从而完成期望的修剪任务。绿篱修剪机械手的运动学分析即研究关节变量和末端修剪刀具的位姿之间关系。
2.1 建立D-H坐标系
为描述机器人相邻连杆之间的位置关系,Denavit[2]等在1955年提出一种通用的方法。1986年Khalil等提出一种改进的D-H方法。两种方法都是在每个连杆上固定一个坐标系,通过依次坐标变换可最终推导出末端执行器相对于基坐标系的空间位姿,从而建立运动学方程。通过改进D-H连杆坐标系方法建立的绿篱修剪机D-H连杆坐标系如图3所示。
2.2 确定D-H参数
结合图3,运用D-H法得到绿篱机的D-H参数和各关节变量如表1所示。根据D-H法则的规定,确定连杆的坐标系位置。

表1 绿篱修剪机的D-H参数和关节变量
绿篱修剪机的正向运动学是根据机械臂的各关节变量求末端修剪装置的位姿。由建立的连杆D-H参数坐标系与D-H参数表推导出机构连杆的D-H坐标变换矩阵和坐标系之间的齐次变换矩阵公式,可求得:
Ti=Rot(z,θi)Trans(0,0,di)Trans(ai,0,0)Rot(x,αi)=
即
(1)
根据齐次变换矩阵式(1)推导出D-H坐标变换矩阵:
(2)
将绿篱修剪机的各连杆变换矩阵式(2)相乘,可得到其运动学方程:
(3)
式中,式(3)右边表示末端连杆相对于基础坐标系的空间位姿矩阵。根据矩阵对应元素分别相等原则可解得:
nX=(cθ1sθ6-cθ4cθ6sθ1);nY=(sθ1sθ6+cθ1cθ4cθ6);nZ=-cθ6sθ4;
oX=sθ1sθ4;oY=-cθ1sθ4;oZ=-cθ4;
aX=-(cθ1cθ6+cθ4sθ1sθ6);aY=(cθ1cθ4sθ6-cθ6sθ1);aZ=-sθ4sθ6;
PX=(d5sθ1sθ4-d3cθ1);PY=-(d3sθ1+d5cθ1sθ4);PZ=d2-d5cθ4;,
(4)
式中,sθi=sinθi;cθi=cosθi。

(5)
由式(5)可看出与绿篱机所处初始位姿一致,所以齐次变换矩阵正确。
2.3 绿篱修剪机逆向运动学求解

(1)求θ1、θ4;由式(4)已知,sθ1sθ4=oX;-cθ1sθ4=oY;-cθ4=oZ得:
(6)
(2)求θ6;由式(4)已知,-cθ6sθ4=nZ;-sθ4sθ6=aZ得:
(7)
(3)求d5;由式(4)已知,(d5sθ1sθ4-d3cθ1)=PX;-(d3sθ1+d5cθ1sθ4)=PY,由待定系数法,提取两等式共同系数d3,根据等式两边对应相等原则确定:
(8)
又根据上述已知式sθ1sθ4=oX,-cθ1sθ4=oY,代入式(8)可得:
(9)

(10)
2.4 蒙特卡洛法求解工作空间
所设计的绿篱修剪机由移动、转动关节组成,而每个关节的移动或者转动都有一定的工作范围,也称关节变量范围,而工作空间的末端位姿是在这个范围内随机取值。因此,采用蒙特卡洛法[4]求解机构工作空间具体实施步骤如下:
(1)确定各关节变量的变化范围(θmin,θman);
(2)确定末端执行器的位姿矩阵:
(11)
式中,位置向量为P=[PX,PY,PZ]。
(3)利用随机函数RAND生成N个0-1的随机点,以(θmax-θmin)*RAND为随机步长,得到各关节变量的随机值为:
θi=θ(i,min)+θ(i,max)-θ(i,min)*RAND,
(12)
式中,θi为关节变量随机值;θmax、θmin为关节变量最大、最小极限值;i为关节数目。
(4)把以上生成的所有关节变量的随机值代入到位置向量,求出N个绿篱修剪机末端参考点在基坐标系中的位置。
(5)调用MATLAB绘图命令,绘制绿篱修剪末端的工作空间仿真图形,即可得到绿篙修剪机末端的工作空间。
3 仿真结果
根据上述对绿篱修剪机的运动学分析计算及运动空间[5]求解步骤,利用MATLAB机器人工具箱[5]模块进行运动空间求解仿真,分别建立回转型绿篱修剪机的机器人模型以及工作空间[6-7]仿真图如图4、图5、图6所示,利用所建立绿篱修剪机模型仿真得到球形轨迹如图7所示。
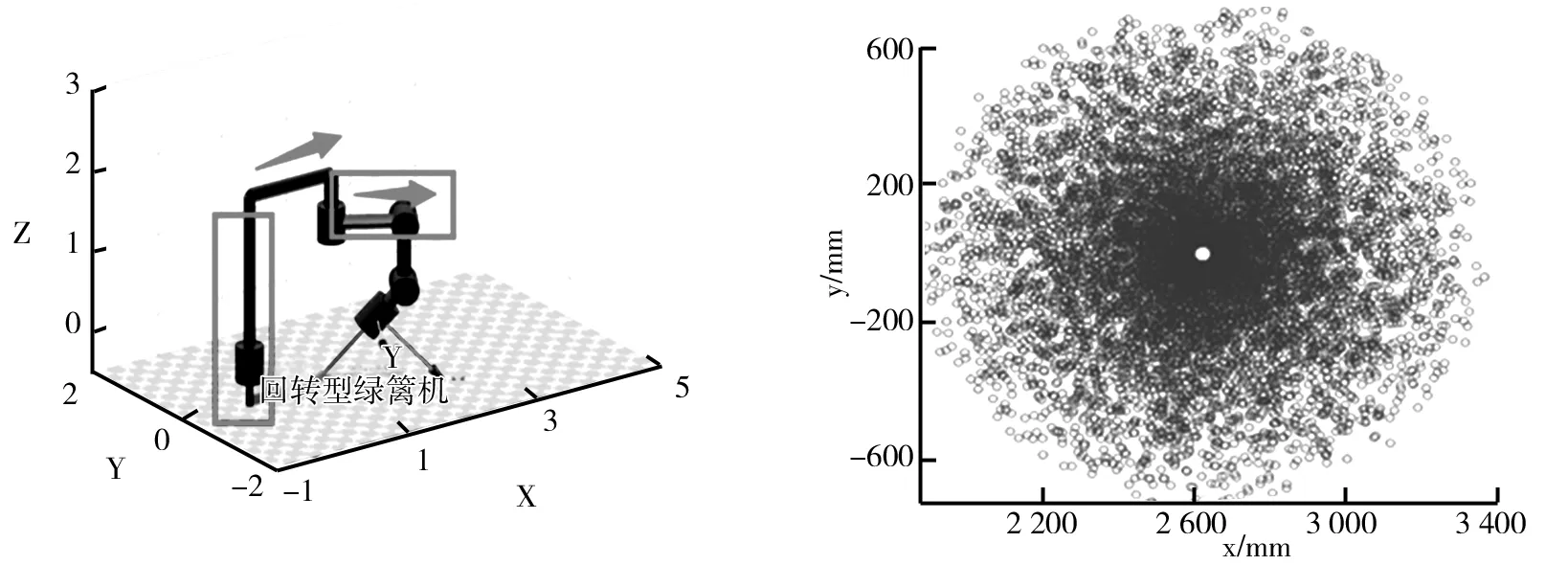
图4 绿篱修剪机模型 图5 绿篱修剪机工作空间XOY平面图
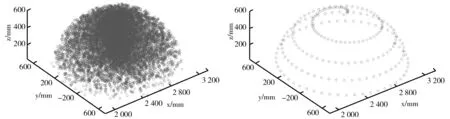
图6 绿篱修剪机三维工作空间 图7 绿篱修剪机球形三维轨迹示意图
由图7仿真结果分析来看,在不考虑障碍物的情况下,用MATLAB[8]机器人工具箱模块来模拟建立的绿篱修剪机模型以及仿真出的工作空间直观、准确表达了绿篱修剪机实际工作空间情况,满足修剪的技术指标要求,也体现了绿篱修剪机设计的合理性、可行性。
绿篱修剪机球形螺旋轨迹运动如图8所示。由图8可知,在MATLAB中通过程序控制绿篱修剪机各关节联动从而生成特定螺旋球形轨迹,以此验证该机构可以完成修剪具有一定几何曲面的绿篱,为进一步进行末端轨迹规划提供理论和模型基础。

图8 绿篱修剪机球形螺旋轨迹运动
4 结论
根据所设计的回转型绿篱修剪机不仅可完成常规横面、侧面绿篱的修剪,还可针对球形等具有几何形状的绿篱进行修剪。在功能上可实现一定范围内不同半径绿篱的修剪,且大大提高修剪效率。首先,在建立绿篱修剪机模型的基础上进行运动学问题分析计算,通过运用改进D-H法建立模型连杆坐标系及参数表。最后,采用蒙特卡洛法及MATLAB机器人工具箱求解并仿真工作空间,直观验证该机构在一定空间范围内运动可行性。
