稳定流作用下的二维海底管道底部冲刷数值分析
2020-03-16张龙珠陈善群
张龙珠,陈善群,廖 斌
(安徽工程大学 力学重点实验室,安徽 芜湖 241000)
随着科学技术的推陈出新以及地表资源的不断消耗,人们将目光逐步投向了覆盖地球面积71%且蕴含丰富能源的海洋。海底管道在人们开采海洋资源的过程中扮演着重要角色,承担起输送石油、天然气等能源的艰巨任务。随着世界工业规模的不断发展以及能源消耗的逐步提高,海底管道的铺设数量越来越多。但同时,海底管道也面临着海洋自然环境的潜在威胁。具体表现在:海洋环境中水流运动的复杂多变驱动海底管道周围泥沙的运动,使得沙床表面的泥沙被卷起并持续输运,在管道底部形成明显的冲刷坑。随着冲刷坑的不断发展加深,海底管道逐渐下垂会引起应力集中,致使管道的悬挑部分会因应力过度或疲劳而发生损坏。显然,研究水流作用下海底管道的底部冲刷具有重要的现实意义和学术价值。
目前已有较多关于水流作用下海底管道底部冲刷的研究成果见诸发表。实验研究方面,学者们分别从冲刷开始的临界条件、尾流冲刷、Keulegan-Carpenter(KC)数、Shields数、多管道以及海底与管道间隙等方面[1-6]对管道冲刷过程进行了实验研究。这些研究工作虽然给出了一些管道冲刷坑的形成规律、影响因素及经验公式,但受到空间尺度的限制,与工程实际存在较大差距。数值研究方面,Nadeem Ahmad[7]等采用开源流体动力学计算软件REEF3D,建立了同向波流作用下管道冲刷的流体动力学计算模型,研究了海底管道下方最大冲刷深度的变化规律,但并未更深入地分析其他参数对冲刷坑深度的影响。史舒婧[8-9]运用FLUENT自定义函数(UDF)模块建立了研究海底管道冲刷的数值模型,着重研究了Shields数对冲刷坑发展以及流场变化的影响,但是由于其对空间、时间离散以及边界条件的一些简化设定,使得数值模拟精度受到一定影响。胡鑫炜[10]利用Open FOAM结合修正的k-ε湍流模型建立了两相泥沙冲刷模型,模拟稳定来流下海底管道的冲刷过程,主要探索了埋置深度对管道冲刷坑形态及深度的影响。此外,周丽丹[11]等采用数值模拟结合实验研究的方法对均匀来流海底管道的冲刷机理以及管道所受振动的特性进行了深入研究,解释了冲刷坑的形成过程,找出了最大冲刷深度所在位置规律,但其总体研究成果主要依据实验研究,对数值方面的探讨不够。
研究拟建立一个求解精度较高,适用于海底管道冲刷的数值计算模型,在对该数值模型进行验证的基础上,分析管道底部冲刷坑初步形成及发育机理。为深入发掘管道底部冲刷的影响因素,对不同流速、水深、管道直径及管道与沙床间隙等条件下,管道底部冲刷坑的位置、深度等规律进行系统研究。研究工作有望为揭示海底管道底部冲刷机理提供信息参考。
1 数值模型
1.1 控制方程
在笛卡尔坐标系下,通过求解不可压缩流体的雷诺时均纳维-斯托克斯(RANS)方程,结合RNGk-ε湍流模型计算获得数值水槽中的流场。控制方程的二维形式如下:
连续性方程:
(1)
动量方程:
(2)
式中,Vf是水体的体积分数;ρ是水体密度,取值1 000 kg/cm3;p为压强;t为时间;u,v是流体沿x,y方向的速度分量;Ax,Ay是x,y方向水体的面积分数;RSOR是质量源项;R,ξ是修正系数,与坐标系的选择有关;Gx,Gy是流体在x,y方向上的重力加速度;fx,fy是流体在x,y方向上的粘滞力加速度。
(3)
(4)
式中,P、G均为湍流动能项(P由水体流速梯度引起,G由浮力引起);kT、εT为扩散项。
1.2 FAVOR处理复杂模型
为精准刻画海底管道的曲面外形、沙床随水流冲刷而产生的形态变化过程以及节约计算资源,选取FAVOR(Fractional Area/Volume Obstacle Representation)网格处理技术进行建模。FAVOR方法即通过单元面积/体积分数精确描述物体复杂外型的方法,是一种独特的网格处理技术。FAVOR方法与有限差分法处理曲面模型的对比如图1所示。从图1中可见,处理相同的几何模型,FAVOR往往仅需较少的网格就可以达到很高的精度要求,但是传统的有限差分法处理曲面模型却要求更多的网格数量,需要更多的计算时间。即使是曲面造型的模型,也可以用矩形网格准确刻画几何外型,确保分析模型不会失真。
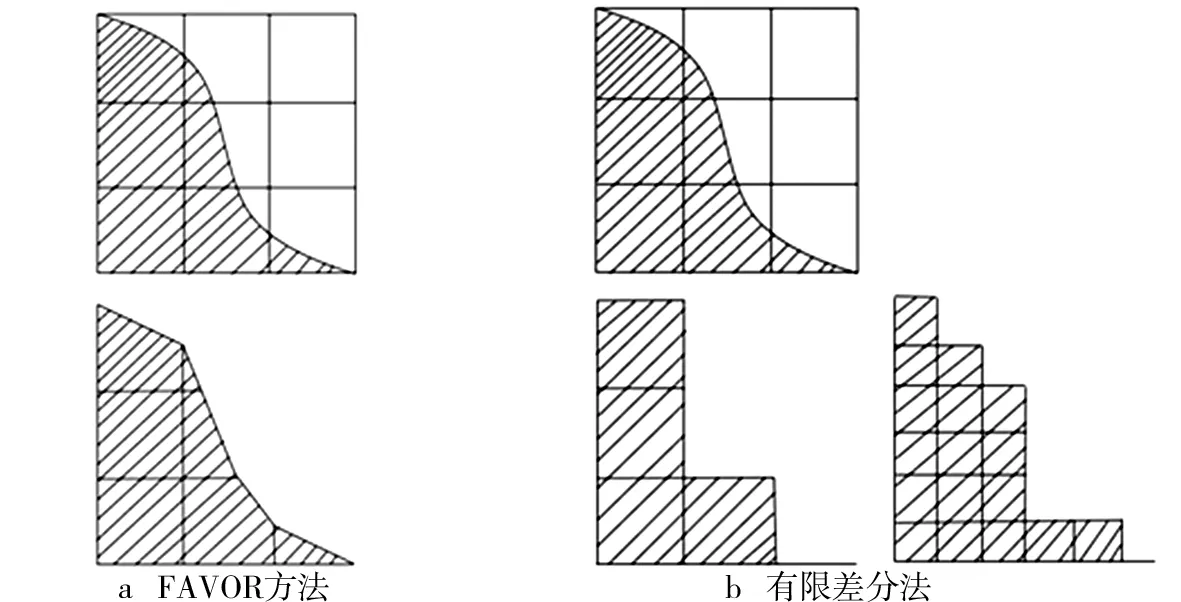
图1 FAVOR方法与有限差分法处理曲面模型的对比
FAVOR方法在求解流体方程的过程中采用7个变量来表征物体几何形状,包括6个面积分数和单元的体积分数。面积分数为单元内空白面积与总面积的比值,体积分数为单元内空白体积与总体积的比值。同时,其能影响包括质量、动量、能量守恒方程以及描述密度、压力、温度耦合情况的状态方程在内的所有控制方程形式,以此获得准确的流体流场变化情况和自由液面运动情况。
1.3 Tru-VOF界面追踪
自从1975年Hirt和Nichols提出Volume of Fluid(VOF)界面追踪方法[12]以来,大多数的流体动力学计算软件在追踪自由界面形态变化时都会采用这一方法。研究所采用的Tru-VOF界面追踪方法是在VOF方法基础上进一步优化而来的。该方法采用的是对流流体算法,不同于VOF方法计算空气-流体的混合动力学性能,而是使用压力或速度边界代替气体部分,不对气体控制方程进行求解,准确追踪流体运动过程中可能出现的尖锐界面,这样既有效节约了计算时间,又一定程度地增加了模拟结果的精度。
Tru-VOF界面追踪方法的主要控制方程如下:
(5)
式中,f是流体分数,其数值范围是0~1之间,f=1代表着单元内充满流体,f=0表明单元内为空气;vf是扩散系数;FSOR是源项。
董爷爷不仅心灵手巧,还是学校里有名的环保达人。有一次冬天我吃完午饭,正巧碰到董爷爷在食堂的水槽边用冰水在清洗碗筷,我就和他打招呼:“董爷爷好,食堂里不是有提供一次性的筷子吗,您为什么不使用呢?”他笑着对我说:“用一次性的东西多不环保呀,而且,我自己带碗筷也方便。”
1.4 泥沙模型
水流中泥沙的输运方式主要分为推移质运动和悬移质运动,其中推移质运动分为跃移质和层移质运动。泥沙模型中模拟泥沙颗粒输运的示意图如图2所示。研究中泥沙冲刷过程的主要计算思路是基于沉积物输运的基本理论,即当沙床剪切应力τ高于临界沙床剪切应力τc时,沉积物沙床上的水流流动会推动沉积物颗粒开始运动。后续通过计算悬移质、重力引起的泥沙沉降以及推移质等来模拟沉积物沙床随水流运动而产生的形态变化。

图2 泥沙输运方式示意图
在水-沙交界面处,由于沙床剪切应力以及漩涡的复合作用,泥沙往往会先被抬升,悬浮后沿水流方向输运。鉴于难以通过流动动力学计算每一粒泥沙的运动轨迹,这里使用Mastbergen[13]等提出的经验模型。临界Shields数θcr,i的大小通过Soulsby-Whitehouse方程[14]计算:
(6)

沙床表面的粗糙度kS与泥沙的中值粒径d50,packed成正比,
kS=croughd50,packed,
(7)
式中,crough是无量纲系数,通常为2.5。
悬移质输运速度的计算是基于经验公式:
(8)
其中,αi是泥沙被水流挟带的系数,据经验模型取0.018[13],θi是局部希尔兹数,根据局部沙床剪应力计算;ns是垂直于沙床表面向外的法向量;ulift,i是推移质转化为悬移质的泥沙量。
在泥沙输运的过程中,泥沙颗粒可能会由于自身重力从悬移质中沉降到沙床上或在推移质输运的过程中静止,从而产生泥沙淤积的现象。研究选取Soulsby[14]提出的沉降速度方程来计算泥沙沉降:
(9)
式中,υf是流体的运动粘度。
推移质输运的方式多为泥沙颗粒在水流冲刷作用下沿沙床滚动、跳跃,并在此过程中经常与沙床表面泥沙进行交换。沙床单宽推移质体积输运率qb,i的计算采用Meyer-Peter[15]提出的公式:
(10)
式中,Φi为无量纲化的推移质输沙率;Φi=βi(θi-θcr,i1.5),βi是无量纲系数,据经验模型取8.0。
2 海底管道底部冲刷坑的形成和发展过程分析
为验证模型本身的精确性与可靠性,选取Mao[1]等所做管道冲刷实验为参照依据,简化的管道冲刷数值水槽示意图如图3所示。水槽长6 m,高0.9 m,由于目的是研究二维管道冲刷过程,所以宽度取一个网格大小,即0.01 m。管道的材料参数设定为固壁(忽略其在冲刷过程中可能出现的形状变化),直径D=0.1 m,在管道前方设置长40 D的泥沙底面,以使管道前方流场充分发展。为了保证出流不对冲刷过程产生影响,管道后方设置长20 D的泥沙底面。由于考虑海底渗流等因素对冲刷过程的影响,故将管道放置于沙床上方0.05 D。静水深0.35 m,水流流向从左至右,进口的边界条件设置为速度边界,水流初始速度为0.25 m/s。同时,为了不让泥沙在入水口处就直接受到水流冲刷作用,在上游入口设置了厚0.01 m,高0.3 m的稳水挡板。下游出口边界条件选择压力边界以设定流体高度保持模拟过程中水位保持不变;底部采用无滑移壁面条件,粗糙度为2.5 d50;顶部选取压力边界,模拟自然环境中大气压对水流流动的影响;其余均为对称边界。数值水槽的底部铺设厚0.3 m的沙床,泥沙的密度为2 700 kg/m3,中值粒径为0.19 cm,Shields数的临界值是0.048,孔隙度为0.4,休止角为32°。数值水槽的整体网格数为116 880,网格大小为0.01 m。为了获得管道冲刷过程中更加精确的数据,在管道前后特别加密了网格(图3虚线之间部分),网格大小为0.005 m。

图3 管道冲刷数值水槽示意图
将数值计算结果与Mao[1]等的实验结果进行了比较,沙床高程结果的对比、模拟过程中流场的压强及速度分量变化如图4所示。图4a、图4b是研究沙床高程数值计算与Mao[1]等实验10 min和30 min的结果对比图。从两者曲线整体来看,数值计算与实验结果呈现出较好的一致性。两者之间存在些许差异是由于管道并未直接放置于沙床表面,而是存在一定间隙,所以管道后方堆积体位置较实验结果略微偏右,但随时间推移该间隙对整体堆积体的位置变化影响可以忽略。同时,由于未考虑海底渗流效应对泥沙颗粒的浮力作用、管道系统以及在冲刷过程中管道表面形状变化对冲刷过程的影响,故冲刷坑深度以及堆积体的高度会比实验结果略高。以上说明,研究数值模型对于海底管道底部冲刷问题具有较好的适用性和较高的计算精度。
图4c、图4d分别为冲刷时间10 min和30 min的流场流线图。从图4c、图4d中可以看出,水流在到达管道之前为均匀来流,靠近沙床的水流速度较低。在遇到管道时,水流出现分流,在管道上下两侧水流速度达到最大,最大值为0.406 m/s。这几乎是入流速度的1.6倍,导致了在管道底部发生射流现象,并因此产生冲刷。在管道后上方,水流速度近似或等于0,形成涡流区,部分悬移质沉降,推移质静止,导致在管道后方逐渐形成淤积。而当淤积泥沙体积逐渐变大时,管道后下方水流速度缓慢变小,堆积体右侧水流速度为负,形成漩涡,减缓堆积泥沙输运。在管道的下游侧,沙床高程与初始高程相近,没有观察到冲刷现象。这是因为沙床上坡度较大的冲刷坑会使水流几乎垂直地从管道下方冲刷而出,避免了漩涡与沙床的相互作用。
图4e、图4f是模拟时间10 min和30 min时的流场压强图。由图4e、图4f中可以看出,由于稳定流作用,管道底部的压强始终较大,为3.6 kPa左右。这也解释了为何在冲刷过程中管道底部冲刷坑深度逐渐增加。结合图4c、图4d以及10 min到30 min的压强均为正压可以看出,相同条件下,随着冲刷时间的增加,管道底部冲刷坑加深,水流流速减小,管道底部沙床所受压强增大。该现象也符合伯努利原理,从侧面验证了数值模型的可靠性。
图4g、图4h是10 min和30 min时的z方向速度分量图。由图4g、图4h中可以看出,在遇到管道之前,水流z方向速度分量为0。遇到管道时,水流分流,部分向上速度达到z方向最大值,部分向下冲刷管道底部沙床,形成冲刷坑,并开始沿水流方向输运泥沙颗粒。虽然部分水流沿冲刷坑坡度流出会给沙床表面泥沙一个z方向的速度,但由于管道后方水流合流,该速度很快为0,导致悬浮泥沙颗粒逐渐沉降形成淤积。这也是管道后方会形成泥沙堆积体的原因之一。

图4 管道冲刷数值结果分析图
从以上结果分析图及验证部分中可以清楚得出稳定流作用下海底管道底部冲刷坑形成和发展的原因。水流在到达管道之前,流场稳定为均匀流,流速大小为设定值。水流在遇到管道时分流,在管道上下两侧水流速度达到最大,并在管道底部出现射流现象,产生冲刷坑。射流沿冲刷坑坡度流出会给沙床表面泥沙一个z方向的速度,但由于管道后方合流,水流产生速度差形成漩涡,导致部分悬移质沉降,推移质静止形成淤积。同时,因为沙床表面冲刷坑坡度较大,射流几乎垂直从管道下方冲出,防止了管道后方由于速度差形成漩涡与沙床再次相互影响,所以只有管道附近沙床会受到影响。
3 海底管道底部冲刷的影响因素
为了更深入地研究海底管道底部的冲刷过程,通过调整验证模型中的流速、静水深度、管道直径以及管道与沙床间隙等参数,进一步探讨相关参数对冲刷坑发展过程产生的影响。
3.1 流速
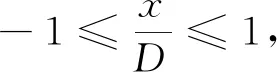
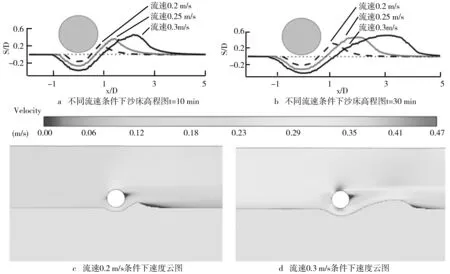
图5 不同入流流速条件下数值结果
3.2 水深
在其他参数设置与验证算例相同时,设置不同的静水水深,海底管道底部冲刷过程的数值结果如图6所示。图6a、图6b分别是模拟时间为10 min、30 min时,在静水深为0.2 m、0.3 m、0.4 m条件下的沙床高程数值结果图。当水深由0.2 m到0.4 m时,管道底部冲刷坑的深度逐渐减小,管道后方堆积体体积缩小,离管道的距离逐渐变小。图6c、图6d为30 min时,水深为0.2 m和0.4 m的流场z方向速度分量图。从图6c、图6d可以看出,随着静水深度的增加,水流在经过管道截面时的流速减小,管道对周围流场的影响逐步减弱。水流分流后,部分向下方冲刷沙床的水流z方向速度分量减小,管道后方射流z方向的流速减小以致水流携带泥沙的能力降低,沙床表面冲刷坑深度变浅。同时,水流经管道后合流速度加快,管道后方淤积泥沙输运速率减缓,堆积体离管道的距离更近。这也就是图6a、图6b两幅图中沙床高程变化的原因。

图6 不同静水深度条件下管道冲刷过程的数值结果
3.3 管道直径
在其他参数设置与验证算例相同时,设置不同的管道直径,海底管道底部冲刷过程的数值结果如图7所示。图7a、图7b分别为模拟时间是10 min、30 min时,在管道直径是0.05 m、0.1 m、0.2 m条件下的沙床高程数值结果图。当管径为0.05 m(即静水深与管道直径的比值h/D=7)时,无量纲化(S/D即冲刷深度/管道直径)后的冲刷深度会比其余两种情况略深,堆积体也会更向右移。而当管径为0.1 m、0.2 m(即h/D≤3.5)时,沙床高程无量纲化后的结果极为相近,冲刷坑深度、范围及形状相似,且随数值模拟时间增长,曲线更为接近。图7c、图7d为30 min时,管道直径是0.05 m和0.2 m的管道冲刷流场速度图。从图7c、图7d可以看出,虽然相同水深条件下,随着管径的增大,水流经过管道横截面时前后流场所受到的影响更大,管道下方水流流速增大,冲刷坑深度也会更深,但是由于管径不同,将冲刷深度无量纲化(S/D)后则可以看出,管径小的冲刷深度反而会更大。

图7 不同管道直径条件下管道冲刷过程的数值结果
3.4 管道与沙床间隙
在其他参数设置与验证算例相同时,设置不同管道与沙床的间隙值,海底管道底部冲刷过程的数值结果如图8所示。图8a、图8b分别为模拟时间是10 min、30 min时,在管道与沙床间隙是0.005 m、0.02 m、0.04 m条件下的沙床高程数值结果图。由图8可知,随着管道与沙床间隙的增大,沙床冲刷坑的深度在逐渐减小,管道冲刷的阶段可以快速从射流期过渡到尾流期[2]。从间隙0.005 m到间隙0.02 m的曲线对比中可以看出,随着管道上移,水流在经过管道时流场的变化也会随之上升,导致冲刷深度减小,产生的射流现象减弱,泥沙输运能力降低以致堆积体积逐渐增大。但从间隙0.02 m到间隙0.04 m的沙床高程曲线对比中可以看出,冲刷坑深度变小,但由于管道与沙床间隙过大,水流流速较快,使得堆积体表面泥沙快速输运,以致间隙0.04 m时的堆积体积较间隙0.02 m的更小。图8c、图8d是30 min时,管道与沙床间隙是0.005 m和0.04 m的流场z方向速度分量图。从图8c、图8d中可以看出,随着管道的上移,管道下方冲刷沙床水流的z方向速度则会降低,输运泥沙能力减弱,导致冲刷坑深度逐渐减小。

图8 不同管道与沙床间隙条件下管道冲刷过程的数值结果
4 结论

