高校学生互联网投资理财影响因素的对数线性模型分析

（齐齐哈尔大学 理学院，黑龙江 齐齐哈尔 161006）

随着互联网技术和信息科技的发展，人们的理财方式逐渐由线下转移至线上，对网络经济的参与度也越来越引人关注.作为未来金融市场主要参与者的高校学生，他们对互联网金融的认知将对未来的经济发展产生很大影响[1]，因而，研究高校在校生对互联网投资理财活动的参与情况是一项具有现实意义的课题.目前，国内学者的研究中，大部分是从描述性分析的角度提出了影响大学生参与互联网金融活动的因素，很多学者只是对学生的投资理财活动进行了描述性分析，又或是分析大学生在选择不同理财产品时的特征.国外学者的研究中，大多是从性别和专业类型入手，以个人特质作为影响因素，研究大学生投资理财活动的参与情况[2].

对数线性模型是建立在列联表统计基础上，以列联表中频数的对数为研究对象，运用类似方差分析的基本思想检验各变量及其交互效应的作用大小，是描述具有非线性相关离散型变量的多元统计模型.该模型可以达到解释对数频数变化成因、拟合对数频数变化规律的目的，可以直接用于分析分类变量的交互效应问题[3].

在以往的研究中，通常使用卡方检验来分析2 个分类变量之间的相关关系，但如果要同时研究多个（3个或3 个以上）变量间的关系，即对高维列联表资料进行分析时，卡方检验就不足以对多个变量间的交互作用给出一个全面的评价，也不可能在控制其它因素作用的同时，对变量的效应做出估计.因而，在变量较多或变量水平较多的情况下，可采用对数线性模型分析主效应和交互效应，对没有统计意义的变量或水平作适当的维数或水平的压缩，将数据简化后可得到多个变量之间的关系.

对数线性模型也存在一定局限性，虽然通过交互效应项可以挖掘出多个变量间的深入关系，比较适合进行探索性分析，但是因为不对自变量和因变量加以区分，若研究变量间存在因果关系，该模型就不再适用[4].另外，如果对数线性模型中包含的变量过多，得到的交互作用会过于复杂，分析结果往往不如线性回归模型容易理解.

本文以高校学生个人特质以及对金融理财活动的体验感为影响因素，通过对不同省份的多所高校在校生进行问卷调查获得数据，将定型变量运用于对数线性模型，分析影响大学生参与投资理财活动的各因素之间的关系，并针对影响因素之间的关联性提出相关的建议，有利于引导高校学生树立正确的投资理财观念，积极理性地投入到互联网金融活动中.

1 数据来源及样本基本信息

1.1 调查对象

调查对象为从黑龙江、上海、北京、湖南、山东等省份为主的多所高校中随机抽取的346 名在校本科生、研究生、博士生.调查对象所学专业覆盖经管类、理工类、文学教育类、音体类以及其它等多种类别.被调查者均以不同形式参与了投资理财活动.

1.2 调查问卷

本文统计数据来源于线上调查问卷，问卷设计参照了以往相关课题的研究内容，并根据本次研究的目的和需求进行自编获得.问卷收集时间为2019-10—2019-11，共回收346 份数据，其中有效数据346 份，有效回收率为100%.问卷内容分为基础信息和参与投资理财的基本状况2 部分[5]，具体包括性别、学历、户口类型、所学专业、理财渠道、对互联网金融风险的了解程度、投资理财的初衷、我国互联网理财平台成熟度、倾向的投资理财方式等.

1.3 样本基本信息

在346 名被调查者中，农村户口人数为219 人，占63.29%，城镇户口人数为127 人，占36.71%；本科生217 例，占62.72%（大一占10.12%，大占二49.13%，大三占1.16%，大四占2.31%），硕士及博士研究生共129 例，占37.28%；对于金融理财风险的了解程度，54.62%的被调查者表示不了解，44.22%的被调查者表示有一定了解，1.16%的人表示非常了解；对于目前我国互联网理财平台的运作成熟度，12.72%的被调查者认为很不成熟，认为不太成熟、比较成熟、十分成熟的人数占比分别为42.49%，42.49%，2.31%.

根据样本信息，得到展示变量数据流动的桑基图（见图1）.

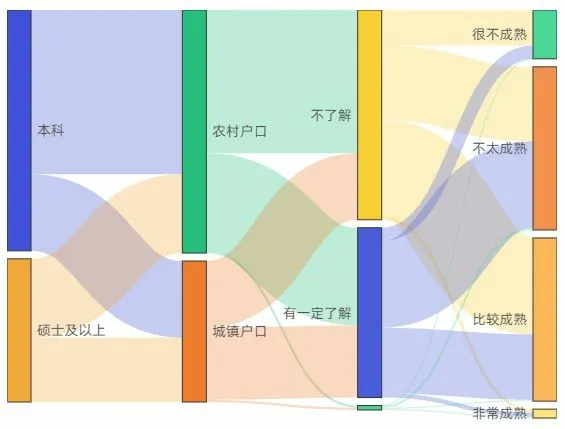
图1 不同变量之间的流程桑基图

图1 展示了不同节点（变量）之间的流量和过程，通过以流动数据的宽度展示数值的大小以及对各组流量运用不同的颜色，桑基图能很好地把各分类数据区分开，方便对样本数据进行定性判断和整体把握.

2 高校学生互联网投资理财影响因素的对数线性模型分析

2.1 数据处理

鉴于以往的相关研究已对被调查者的性别、所学专业、理财渠道、理财方式和投资理财初衷等问题做了充分的研究，且分析已表明这些变量的独立影响较大，而变量间的交互关系并不大.因而主要对学历、户口类型、对金融理财风险的了解程度、我国互联网理财平台的成熟度4 个变量进行存在交互效应的对数线性模型分析，对所要研究的4个变量的各个水平分别进行赋值，结果见表1.

表1 4个变量的各个水平的赋值

将数据资料进行分类统计分析，建立四维列联表（见表2）.以列联表中单元格频数的对数为因变量，以学历、户口类型、对金融理财风险的了解程度、我国互联网理财平台的成熟度及其交互效应为自变量，建立饱和对数线性模型，采用逐步向后剔除法从最高阶交互效应项开始逐步剔除不具有显著性差异的交互效应项，直到保留下来的各效应存在统计学意义，最终形成一个非饱和的最优对数线性模型[6].本文采用SPSS 22.0 统计软件进行数据分析.检验水平为α=0.05.

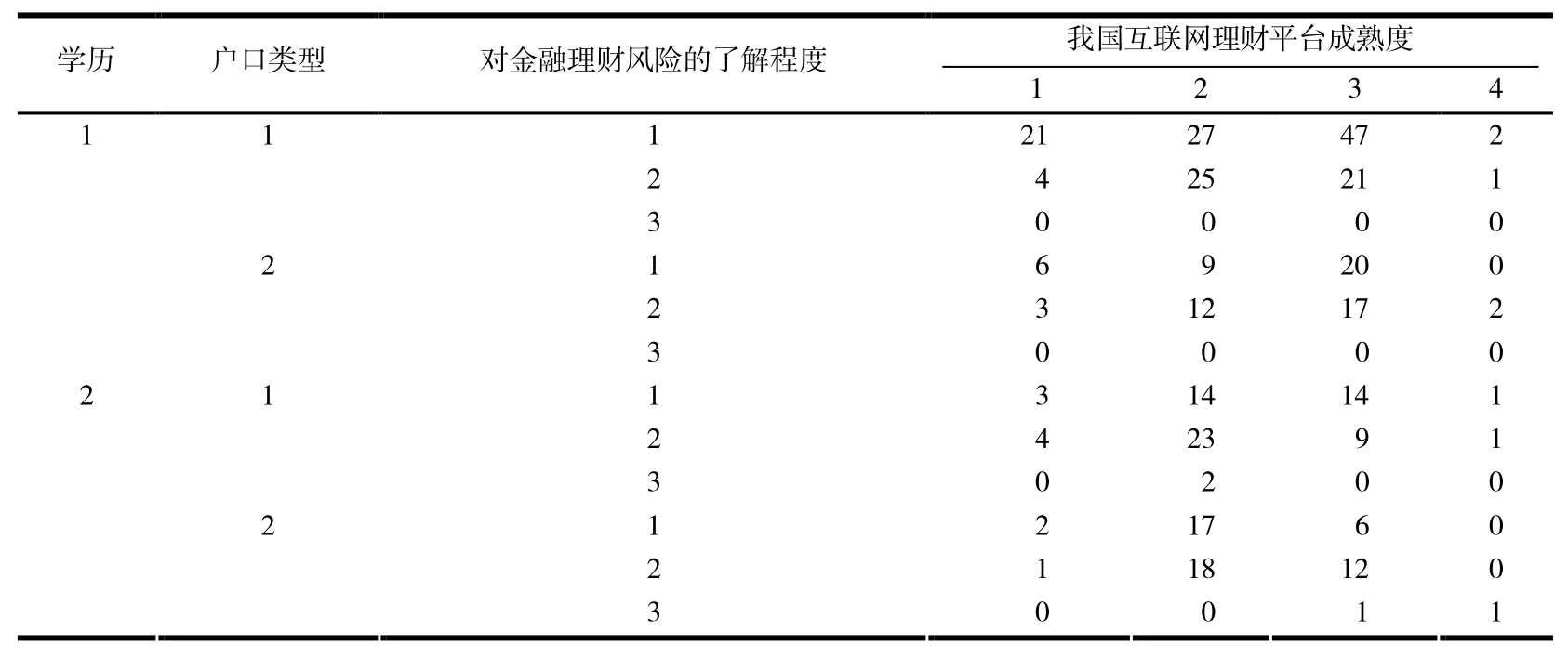
表2 互联网理财平台成熟度与学历、户口类型、风险了解程度关系的四维列联表

2.2 对数线性模型分析

2.2.1 最优对数线性模型的选择和模型的拟合优度检验 将被调查学生的学历、户口类型、对金融理财风险的了解程度、互联网理财平台的成熟度4个变量纳入对数线性模型.得到的饱和对数线性模型为

其中：f为被调查高校学生在学历、户口类型、对金融理财风险的了解程度、互联网理财平台成熟度这4个因素存在关联关系下单元格的频数；λ为对数频数的总理论值；λA,λ B,λ C,λD分别为学历、户口类型、对金融理财风险的了解程度、互联网理财平台成熟度的主效应；λAB,λAC,λAD,λBC,λBD,λCD分别为相应2个变量的一级交互效应；λABC,λABD,λACD,λBCD分别为相应3 个变量的二级交互效应；λABCD为4 个变量的三级交互效应.然而饱和模型中通常存在某些效应项对解释频数分布没有显著的统计学意义，因此应尽量剔除那些不显著的效应项，建立相应的非饱和层次模型.

通过SPSS 软件运行Model Selection 过程，逐个剔除饱和对数线性模型中没有显著意义的三级、二级和一级交互效应项[7]，以剔除交互效应项前后两模型的似然比之差为χ2值，自由度之差作为自由度，判断是否剔除该交互效应项，直至得到最优对数线性模型.

根据逐步向后剔除法得到的非饱和最优对数线性模型为

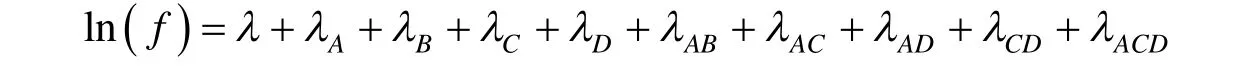
最优对数线性模型的拟合优度检验结果见表3.

表3 拟合优度检验

由表3可以看出，χ2=8.827，P=1.000，大于0.05，表明最优对数线性模型有很好的拟合效果.

2.2.2 最优对数线性模型的参数估计 获得最优对数线性模型后，再采用General 过程得到具体的参数估计和检验结果，进一步对筛选出的主效应和交互效应项逐一进行分析.当主效应和交互效应的系数大于0时，表明该项的变化对因变量的变化为正效应，其作用是使对应的频数增加；当系数小于0 时，为负效应，其作用是使相应的频数减少[8].

参数估计的具体结果见表4.

表4 参数估计

两两变量的不同水平之间会产生多种交互组合，表4 只显示相同变量不同组合中的一种组合形式的参数估计值，未显示数字的估计值代表的交互组合是冗余的或参照的，故系数及其统计量均设为0.由表4可以看出，当以A=2（学历为硕士及博士研究生）为参照时，A=1（学历为大学本科）的系数为-15.378，P值为0.000，小于0.05，即学历系数与0 的差异是显著的，说明该变量存在统计学意义；以A=2 的参数系数值为0 时作为平均参照，得到A=1 时的系数值为负数，说明学历为大学本科的学生比学历为硕士及博士研究生的学生对互联网投资理财的参与程度低.

一级交互效应中，以AB（学历×户口类型）交互项为例，当以[A=1]× [B=2]，[A=2]× [B=1]，[A=2]× [B=2]为参照时，[A=1]× [B=1]（大学本科学历与农村户口的交互效应项）的系数为0.501，P值为0.037，小于0.05，说明该交互项效应系数与0 的差异存在统计学意义.以AC（学历×对金融理财风险的了解程度）交互项为例，当以[A=1]× [C=2]，[A=1]× [C=3]，[A=2]× [C=1]，[A=2]× [C=2]，[A=2]× [C=3]为参照时，[A=1]× [C=1]（大学本科学历与对金融理财风险的了解程度为不了解的交互效应项）的系数为16.224，P值为0.000，小于0.05，说明该交互效应系数与0 的差异存在统计学意义，即大学本科学历的学生对金融理财风险的不了解程度高于平均水平，也就是说，学历为大学本科的学生比学历为硕士及博士研究生的学生对金融理财风险的了解程度更低.由SPSS 的模型运行结果可知，其它变量或交互项的估计参数的P值均大于0.05，均不存在显著的统计学意义，这里不再赘述.

3 建议

通过对数线性模型，研究发现学历与对金融理财风险的了解程度存在交互作用，较低的学历易导致对金融理财风险的了解程度也较低.对此，为了提高高校学生对互联网金融风险的了解，扩大学生对投资理财活动的认知，号召更多的大学生积极理性地参与互联网理财，提出以下对策建议：

3.1 加大对学生的投资理财教育力度

优化高校课程安排，加大对学生的投资理财教育力度.尤其应有规划地针对本科生开设投资理财相关课程，对不同年级的学生采取不同的教育方案.如低年级学生由于经济来源有限，个人储蓄较少，对风险的承受能力较低，理财观念相对薄弱，因而可通过多学习保守稳健型的投资理财方案来调动学生的积极性.

3.2 选择个性化的理财产品

实施组合投资，选择个性化的理财产品.鉴于硕士及博士研究生对风险的了解程度和承受能力更高，而本科生的风险了解程度和承受能力相对较低，建议向学生普及多种类型的理财产品，在选择理财产品时，针对个人情况选择合适的投资组合，如本科生可多选择风险中立型的低风险、低收益的理财产品，同时避免理财产品选择的过分单一化，有效分散风险.

3.3 多途径培养大学生的投资理财意识

多途径培养大学生的投资理财意识，学校在开设互联网理财相关课程的同时，可定期举办相关主题的论坛或讲座等活动，普及各类金融风险知识，提高学生辨别各类理财产品风险的能力以及对理财行为的认知度；大学生个人要注重对投资理财知识和实践经验的积累，培养理财意识和习惯，在进行投资理财行为时向有经验的教师咨询，积极参加校内外专家和理财专业人士组织的相关论坛，丰富理财阅历[9].