基于分数阶忆阻器的4D-Hopfield神经网络动力学分析

丁大为 江丽 胡永兵 杨宗立

基于分数阶忆阻器的4D-Hopfield神经网络动力学分析

丁大为1,2江丽1胡永兵1杨宗立1

（1.安徽大学电子信息工程学院，安徽合肥，230039；2. 安徽大学农业生态大数据分析与应用技术国家地方联合工程研究中心，安徽合肥，230000）

忆阻Hopfield神经网络是研究人脑行为的一种重要模型。研究人员运用Caputo分数阶微分定义，将整数阶双曲型忆阻器推导至分数阶双曲型忆阻器，同时验证了它的忆阻特性，并且提出了分数阶忆阻Hopfield神经网络。对该模型的平衡点与稳定性的理论分析，表明了系统具有多个平衡点的特点。此外，运用Adams–Bashforth–Moulton算法对所提出的分数阶忆阻Hopfield神经网络系统进行的相图及时域图的数值仿真，揭示了在不同耦合强度、不同分数阶阶次下系统展现出复杂的动力学行为。

双曲型忆阻器；分数阶；Hopfield神经网络；动力学行为；数值仿真

引言

相较于电阻器、电感器以及电容器而言，被称为第四基本电路元件的忆阻器的特点是能够记住流经它的历史特性，同时这也是忆阻器名字的由来[1]。自忆阻器被惠普实验室研究出来，忆阻器便成为了研究的热门。直到今天，忆阻器在神经网络的研究中也占领着重要的地位[2]。

Hopfield神经网络具有类似人脑的信息储存功能，因此Hopfield神经网络被列为研究人工神经网络的重要的模型之一[3]。近年来，随着Hopfield神经网络在科学理论和工程应用中的广泛使用，忆阻器在神经网络中的作用也愈加显著。因此，研究忆阻Hopfield神经网络模型对当下和未来的科学发展都具有相当重要的意义[4]。

相较于整数阶的微积分而言，在系统中引入分数阶微积分会更准确地描述实际系统的特性[5]。同时，因为分数阶微积分中存在记忆项，这使得分数阶微积分被认为是描述遗传和记忆特征极好的工具[6]。而忆阻器及Hopfield神经网络也有记忆存储的功能，那么将分数阶微积分与忆阻Hopfield神经网络结合在一起，将有可能更大程度上地提高记忆特性及信息处理效率[6]。

本研究的主要内容是将整数阶双曲型忆阻器拓展至分数阶双曲型忆阻器，并且引入到Hopfield神经网络，构成了忆阻Hopfield神经网络并分析了系统的平衡点与稳定性。通过系统相图数值仿真，对系统的稳定性表现进行研究，其组织结构如下：第一部分介绍了Caputo分数阶微分定义、分数阶稳定性判定方法以及双曲型忆阻器的模型，从而推出分数阶双曲型忆阻器，进而构造出分数阶双曲型忆阻Hopfield神经网络系统；第二部分分析了系统的平衡点和稳定性；第三部分通过相图和时域图的数值仿真，分析了耦合强度与分数阶阶次对系统稳定性的重要影响。

1 分数阶忆阻FNN模型

1.1 预备知识

定义1[7]Caputo分数阶微分定义如下：

引理1[8]如果平衡点处的雅克比矩阵的任一特征值满足

这意味着系统在平衡点处是渐进稳定的。

1.2 双曲型忆阻器模型

双曲型忆阻器的本构关系[9]如下：

根据Caputo分数阶微分定义，推导出的分数阶双曲型忆阻器的模型如下，

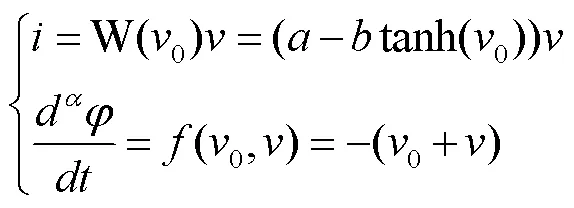
考虑电压源为正弦电压源，和分别表示激励的振幅和频率。运用Adams–Bashforth–Moulton（ABM）算法进行数值仿真，取忆导函数中，，并且令。当振幅保持不变时，设置频率分别为500、1、2,可得电流与电压的关系()曲线如图1(a)所示；当频率保持不变，设置振幅分别为1、2、3，可得曲线如图1(b)所示。

1.3 分数阶双曲型忆阻FNN

新型的Hopfield神经网络的模型[10]可用矩阵的形式表示，

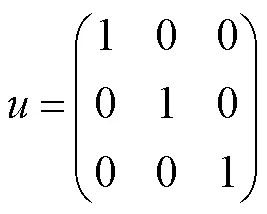
2 平衡点和稳定性分析

令（8）式左边为0，如下所示：

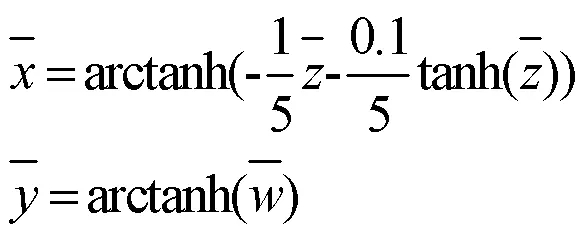
因此，以为例，绘制了等式(11)给出的两条函数曲线，如图2所示，红色代表曲线，蓝色代表，则三个交点确定的分别为，，，，，。

根据以下方程可以进一步求得系统的特征值：

其中，

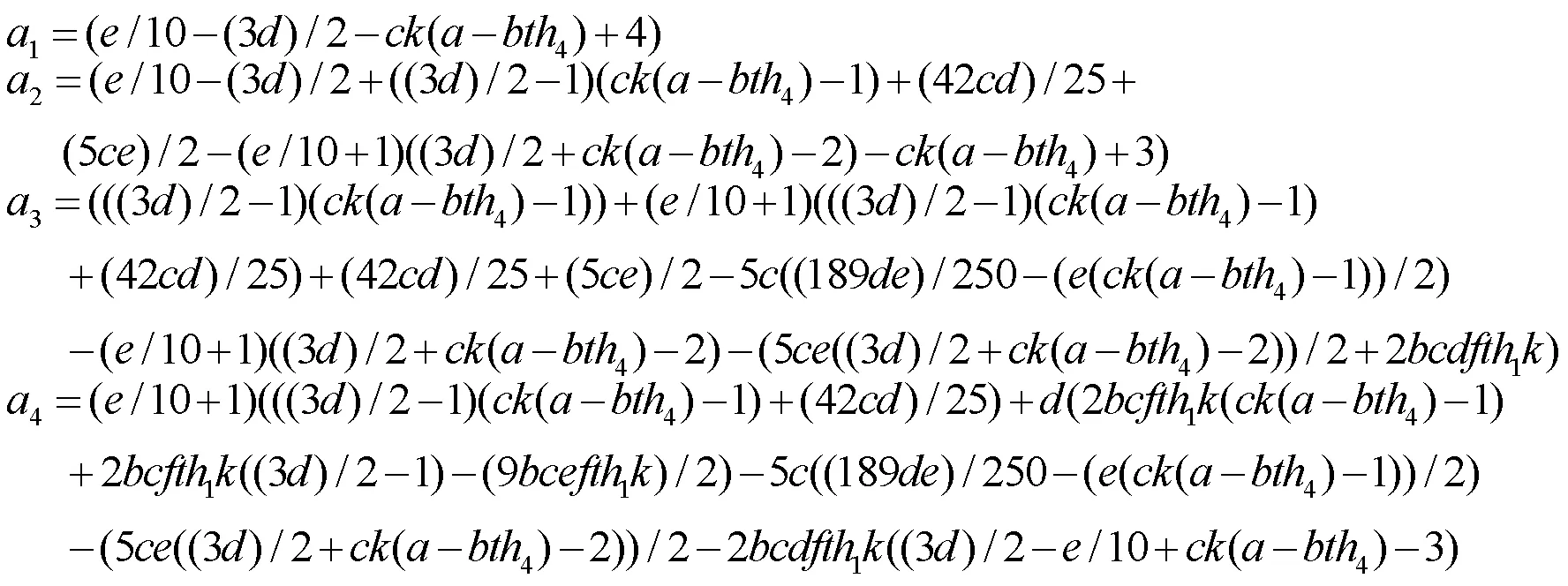
表1 不同值下的非零平衡点、特征值以及稳定性（）

3 数值模拟

3.1 耦合强度对系统稳定性的影响

图3 在不同耦合强度下平面相图的数值仿真

从图3的相图可以看出，由于耦合强度的不同，系统在不稳定状态下表现出周期或者混沌的现象，这与上文在不同的耦合强度下系统将会表现出不同的稳定性的理论分析相呼应，并且这也体现出在神经网络中突触重量影响着大脑的神经活动。

3.2 分数阶阶次对系统稳定性的影响

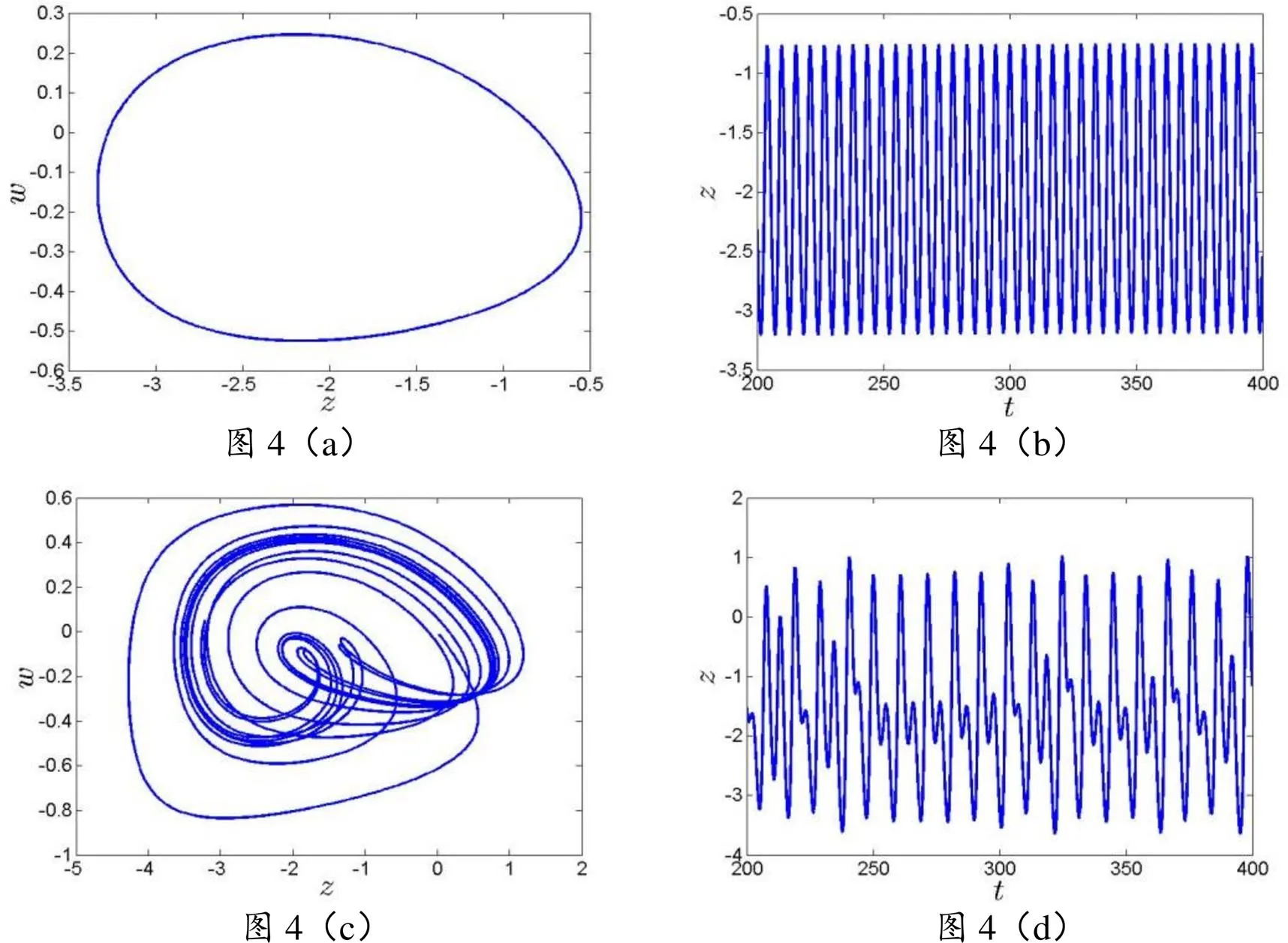
图4 在不同分数阶阶次下平面相图和相应的时域图的数值仿真

4 结论

本研究提出了一个分数阶双曲型忆阻器的Hopfield神经网络，并在理论和数值模拟上对此系统进行研究。针对系统的平衡点与稳定性的理论研究表明：该系统具有多个平衡点，并且系统的稳定性与耦合强度有关。相图和时域图的数值仿真结果表明：在不同的耦合强度与不同的分数阶阶次下，该系统在不稳定的状态下不仅存在不同的混沌状态，而且还存在周期状态。

[1] 王春华,蔺海荣,孙晶如,等. 基于忆阻器的混沌、存储器及神经网络电路研究进展[J]. 电子与信息学报, 2020,42(4):795-810.

[2] 王小平,沈轶,吴计生,等. 忆阻及其应用研究综述[J]. 自动化学报, 2013,39(8):1170-1184.

[3] 陈墨,陈成杰,包伯成,等. 忆阻突触耦合Hopfield神经网络的初值敏感动力学[J]. 电子与信息学报, 2020,42(4):870-877.

[4] Ma C, Mou J, Yang F, et al. A fractional-order Hopfield neural network chaotic system and its circuit realization[J]. The European Physical Journal Plus, 2020, 135(1):100-115.

[5] 廖洪运. 基于三次非线性忆阻器的分数阶蔡氏电路动力学特性[J]. 中国新通信, 2018,20(14):222-223.

[6] Hu H P , Wang J K , Xie F L . Dynamics Analysis of a New Fractional-Order Hopfield Neural Network with Delay and Its Generalized Projective Synchronization[J]. Entropy, 2018, 21(1):1-12.

[7] 俞亚娟,王在华. 一个分数阶忆阻器模型及其简单串联电路的特性[J]. 物理学报, 2015,64(23):369-377.

[8] 廖洪运. 基于三次非线性忆阻器的分数阶蔡氏电路稳定性分析[J]. 通讯世界, 2018(3):139-140.

[9] Z.T. Njitacke,J. Kengne. Complex dynamics of a 4D Hopfield neural networks (HNNs) with a nonlinear synaptic weight: Coexistence of multiple attractors and remerging Feigenbaum trees[J]. AEU - International Journal of Electronics and Communications, 2018,93:242-252.

[10] Njitacke Z T , Kengne J . Nonlinear Dynamics of Three-Neurons-Based Hopfield Neural Networks (HNNs): Remerging Feigenbaum Trees, Coexisting Bifurcations and Multiple Attractors[J]. Journal of Circuits, Systems and Computers, 2019,28(7):1950121.1-1950121.27.

Dynamical Analysis on 4D-Hopfield Neural Network Based on a Fractional-order Memristor

DING Dawei1,2& JIANG Li1& HU Yongbing1& YANG Zongli1

The memristive Hopfield neural network is an important model for studying human brain behavior. Researchers pushed the theory of hyperbolic-type memristor from integer-order to fractional-order by use of the Caputo fractional-order differential definition, and verified its memristive characteristics. On this basis, the fractional-order memristive Hopfield neural network is proposed. The theoretical analysis on the equilibrium point and stability of this network presented that the network has multiple equilibrium points. Meanwhile, the numerical simulation of the phase diagrams and time domain figures of the fractional-order memristive Hopfield neural network by means of Adams–Bashforth–Moulton method reveals that the complex dynamic behavior of the system in different coupling strength and fractional orders.

hyperbolic-type memristor; fractional-order; Hopfield neural network; dynamic analysis; numerical simulation.

TP183

A

1009-1114（2020）03-0001-06

2020-04-29

丁大为（1977.9—），安徽芜湖人，博士，安徽大学电子信息工程学院教授、硕士生导师，国家自然科学基金通讯评审专家，研究方向为非线性电路、忆阻混沌系统、无线通信及通信仿真等。

文稿责编 濮荣强