优化问题结构 建构数学概念

覃献华

“认识分数”是学生学习新知的起始课，在知识的建构上借助问题结构图，能更好地帮助学生建构数学概念，更好地对学生以启迪.

【设计】

一、忆旧引新，启迪思维

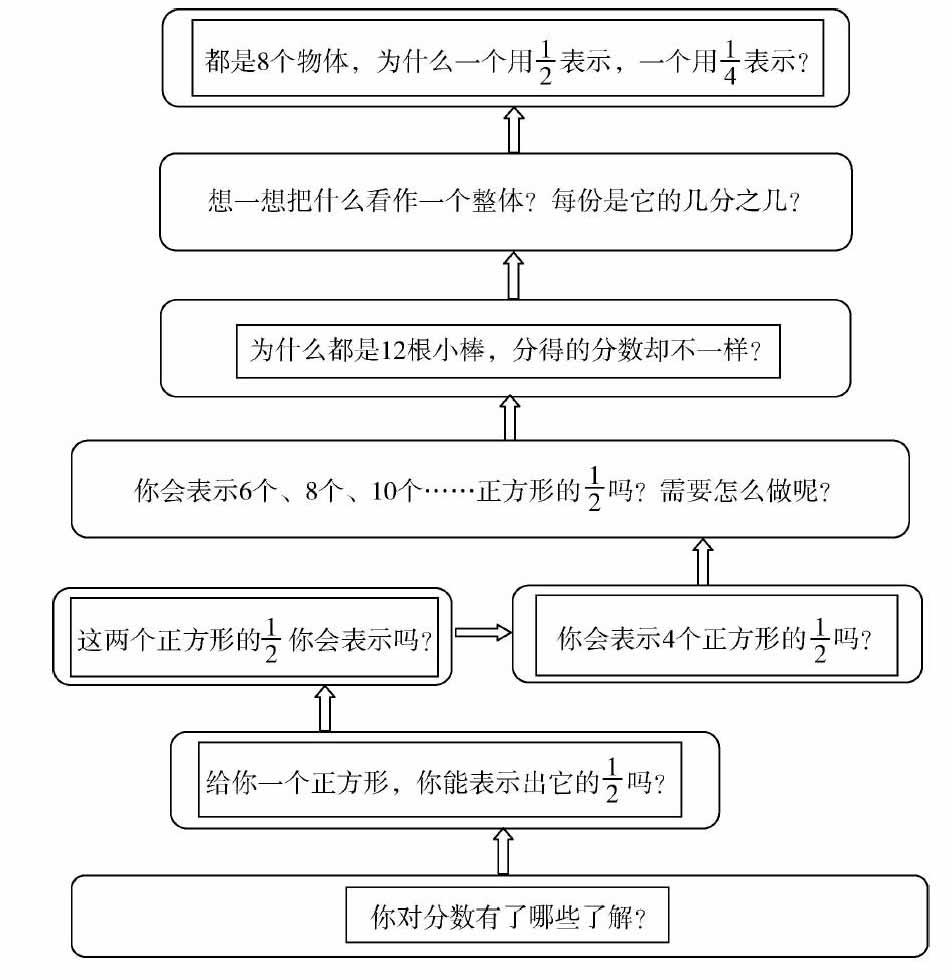
教师：“你对分数有了哪些了解？”

学生回答：“把一个苹果平均分成两份，每份就是它的12.”

教师：“如果给你一个正方形，你能表示出它的12吗？”

学生自己在作业纸上完成后，给教师展示.

教师：“谁能知道这两名学生分别是怎么想的？”

教师总结：“把一个物体平均分成两份，每份就是它的12.”

二、自主探究，形象感悟

出示：

教师：“这两个正方形的12你会表示吗？”学生在作业纸上完成，教师指导后让学生汇报自己的想法和分法.

分法一：

教师让学生按划圈的提示补上.

教师再出示分法二：

教师：“这样表示对不对？为什么？这里平均分成的是几份？”

让学生和教师一起总结，把两个正方形平均分成两份，每份就是它的12.

教师：“你会表示4个正方形的12吗？”

出示：

让学生自主完成并汇报.

教师：“你会表示6个、8个、10个……正方形的12吗？需要怎么做呢？”

三、活化思维，数形结合

出示：

教师：“你能表示出几分之几？”

学生说出几个分数如：12，13，14，112.

教师：“你会表示吗？”

学生在作业纸上表示后，教师让学生思考：为什么都是12根小棒，分得的分数却不一样.

四、操作比较，形象思辨

教师出示：

教师：“想一想，把什么看作一个整体？每份是它的几分之几？”

再出示：

教师：“都是8个物体，为什么一个用12表示，一个却用14表示？”

【评析】我们知道在数学知识的学习中，数是非常抽象的，分数更是如此，让学生在思维发展中认识和理解分数，分数的概念才能得到很好的建构.这不同于“角的认识”它需要教师为学生提供充分的形象感知， 建立表象，理解意思，打通抽象知識与形象思维之间的障碍.因此，第一课时“认识一个物体的几分之一”是基础，把几个物体看成一个整体，得出几分之一，对于学生来说难度非常大，思维的跳跃度很高， 需要教师分别就两个正方形， 四个正方形，甚至

六个、八个正方形等等充分引导，启发学生的感悟理解“不管是几个物体，要得到它的二分之一，只要把它平均分成二份，每份就是它的二分之一.”让学生在充分操作、比较中建立“把一些物体看作一个整体”，这里既不是线型的，也不是围着一个中心的讨论，是一个反复感悟的过程，充分利用数形结合思想，让抽象的分数在形象图形的刺激下在学生大脑中留下深刻的印记.

在本节课中，学生对于分数的知识建构可以用下面的问题结构图表示，更能呈现出本节课的问题结构的特点：

分数作为数，它的本质是非常抽象的，如何让抽象的分数可观、可感、可悟，需要借助于形象化的物体、图形，然后在平均分的过程中一步步认识、理解分数，使学生理解虽然物体的个数不同，却可以用相同的分数表示，因为他们平均分的份数相同.而物体的个数相同，却可以用不同的分数表示，因为平均分的份数不同.分数抽象的本质属性让学生在形象图形平均分的过程下看得清清楚楚，在一连串的问题结构模式下，对分数的认识深入浅出，理解透彻.在实际教学中，“因数和倍数”“梯形的面积计算公式”等知识也可以采用本节课的问题结构图进行问题设计，以期提高教学效果.