Microsoft Mathematics软件在高职高专高等数学绘图中的应用研究

钱小慧

【摘要】Microsoft Mathematics软件是一个拥有强大计算和绘图功能的数学软件，相当于一个手持计算器.本文首先介绍了Microsoft Mathematics软件，接着探究了Microsoft Mathematics软件在高等数学绘图中的应用，列出了使用Microsoft Mathematics软件绘制函数的图像，帮助学生更好地理解抽象的极限概念，从图像上直观地求函数的极值，绘制出曲线围成的封闭图形，方便利用定积分求平面图形的面积.

【关键词】高等数学;Microsoft Mathematics软件;绘图;高职高专

【基金项目】云南省高教学会高职高专教育分会第四批高职教育科研课题：Microsoft Mathematics软件在高职高专高等数学中的教学研究.项目编号：2018YGZ69.

高等数学教学与数学软件的应用相结合是当前的一个热门课题.目前使用的主流高等数学软件有MATLAB、Mathematica、Maple等[1].它们的优点是可以解决大量的数学问题，被广泛地用作主流高等数学教科书中的应用软件[1].但是它们的缺点和优点一样的突出，表现在正版昂贵，一般学校都很少有，软件一般占用内存比较大，对电脑硬件有比较高的要求，使用较为烦琐，难度较大，对高职高专学生及普通大众而言，Microsoft Mathematics软件简便易操作，占用空间小，软件本身对硬件的要求较低，正版软件获得比较容易，可以免费从微软中国官方网站上下载得到[1].Microsoft Mathematics软件的最新版本是4.0，该版本的下载地址为：

一、Microsoft Mathematics软件简介

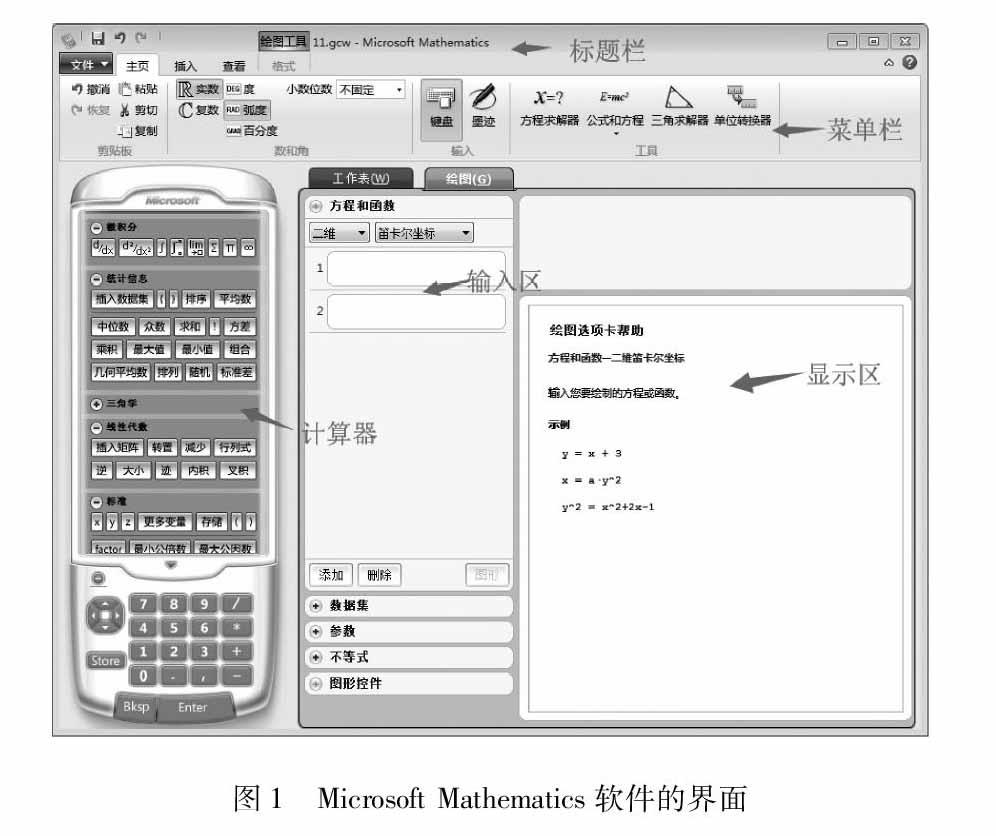
Microsoft Mathematics软件是一个拥有强大计算和绘图功能的数学软件，相当于一个手持计算器.界面如图1，它毕竟是微软自己的软件，在操作使用上，很容易上手.软件的主要功能包括：

1.数值计算.该数学软件能够计算有理数、无理数，能够对实数、复数、微积分计算，能够进行精确或近似计算，也能解方程、方程组及不等式.2.直观形象的绘图.可以绘制笛卡尔坐标、极坐标、圆柱体、球体等各种坐标系下的三维和增强的三维彩色图形.本文主要研究Microsoft Mathematics软件在微积分计算中的应用.

二、Microsoft Mathematics软件在高等数学绘图中的应用

本文主要介绍Microsoft Mathematics软件在高等数学绘图中的应用.以下是Microsoft Mathematics软件在高等数学绘图中的应用案例.Microsoft Mathematics还有强大的计算功能，本文就不举例说明了.

（一）利用Microsoft Mathematics软件绘图，帮助学生理解极限概念

极限是微积分中的重要概念，它指的是变量在一定的變化过程中，从总的来说逐渐稳定的一种变化趋势以及所趋向的值（极限值）.极限的概念最终由柯西和魏尔斯特拉斯等人严格阐述.在现代的数学分析教科书中，几乎所有基本概念（连续、微分、积分）都是建立在极限概念的基础之上.极限的概念比较抽象，极限的计算较复杂，且无法想象出这些函数的图像，教师可以在讲解极限的过程中，利用软件画出这些函数的图像，有利用学生理解极限的运算结果.

利用Microsoft Mathematics软件绘图的操作步骤为：1.点击该软件界面“绘图”按键;2.再点击下一行的“方程和函数”按键;3.然后在空白工作域输入要绘制图像的函数表达式;4.单击“图形”按键，得到函数的图像.

（二）利用Microsoft Mathematics软件绘图求极值

函数极值是推动微积分发展的重要内容之一，在科学技术和社会生活的各个领域中，充满了函数极值问题.如能量最小、最佳拟合、最短路径、时间最短等问题，都可以转化为函数极值问题.确切地说，这里讨论的只是“局域极值”问题，“全域最值”问题要复杂得多.至今没有一个“系统性”的方法可求解一般的“全域最值”问题.一般地，运用一阶导数求一元函数极值的一般步骤为：1.确定函数定义域并找出所给函数的驻点和导数不存在的点;2.考查上述点两侧导数的符号，确定极值点;3.求出极值点处的函数值，得到极值.

现在数学教学应遵循“以应用为目的，理论知识以必需、够用为度”的原则，注重应用.因此，在教学过程中可以将Microsoft Mathematics软件引入课堂，引导学生运用现代信息技术手段解决问题.

（三）利用Microsoft Mathematics软件绘图，用定积分求面积

运用定积分求面积，其关键是确定出被积函数和积分的上、下限.一般应是先根据题意，借助图形的直观性确定出被积函数，求出两条曲线的交点坐标，确定积分的上、下限，进而由定积分求出其面积.利用Microsoft Mathematics软件很容易就绘制出函数的图像，从而方便利用定积分求面积.

例3 利用定积分求由曲线y=x和直线y=x所围成的平面图形的面积.

从以上这些例题可以看出，Microsoft Mathematics软件易学、好用、操作简便，是辅助教学的好工具，尤其是它的图形输出功能可以帮助学生更直观地解决高等数学中的一些绘图问题，增强课堂信息的表现力.

高职高专教育的根本任务是培养适应生产、建设、管理、服务等一线的高等技术应用型人才[3].数学作为一门公共基础课程，不仅为后续专业课程的学习打下基础，提供必需的数学知识与方法，还具有较强的工具性与实用性，为专业课服务.利用Microsoft Mathematics软件来辅助高等数学的教学，能更好地发挥数学的工具作用.

【参考文献】

[1]姬天富，刘震，张华伟.Microsoft Mathematics软件在高等数学辅助教学中的案例探究[J].连云港职业技术学院学报，2017（3）：74-76，80.

[2]盘俊春.数学和科学研究的实用工具：Microsoft Mathematics[J].中国信息技术教育，2014（9）：67-69.

[3]任安忠.高职院校高等数学教学方法的研究和探讨[J].张家口职业技术学院学报，2008（1）：52-54.