把握规律本质，发展归纳推理思想

李巧仪

归纳推理，是从特殊到一般的推理方法，即依据一类事物中部分现象的相同性质推出该类事物都具有这种性质的一般性结论的推理方法.“植树问题”是小学数学第二学段的学习内容，在归纳推理思想的渗透中要让学生经历归纳推理的过程并且发展其归纳推理能力.在课堂上教师让学生通过观察和分析发现教师给出的图片中树和间隔数一一对应，从而归纳推理得出植树问题的核心——树和间隔一一对应的关系，并且能够把这个结论应用在与“植树问题”相关的一类问题中.在授课时，教师应有目的地为学生助力，帮助学生把握好问题的规律和本质，发展学生的归纳推理思想.

一、分析生活问题，感知发现规律本质

数学课程标准（2011年版）指出：“课程内容的选择要贴近学生的实际，有利于学生体验与理解、思考与探索.”作为数学教师，要善于依据教学内容捕捉生活实例，为学生和课堂提供有效的例证.在课堂教学中，通过分析生活中的实际现象，引领学生感知和发现“植树问题”中树与间隔成一一对应关系的规律和本质.

【片段一】

教师课件出示一组行道树图片

师：同学们，你们看这些图片，如果让你们到路边种树，你觉得该怎么种？

生1：树与树之间要隔开一段距离.

生2：我觉得樹与树之间不仅要隔开一段距离，而且隔开的距离应该是相等的.

生3：我觉得路的首端和末端都要种上树.

师：很好，通过你们的分析，我们来研究一下到底该怎么种树.

教师一边用课件演示，一边和学生交流：

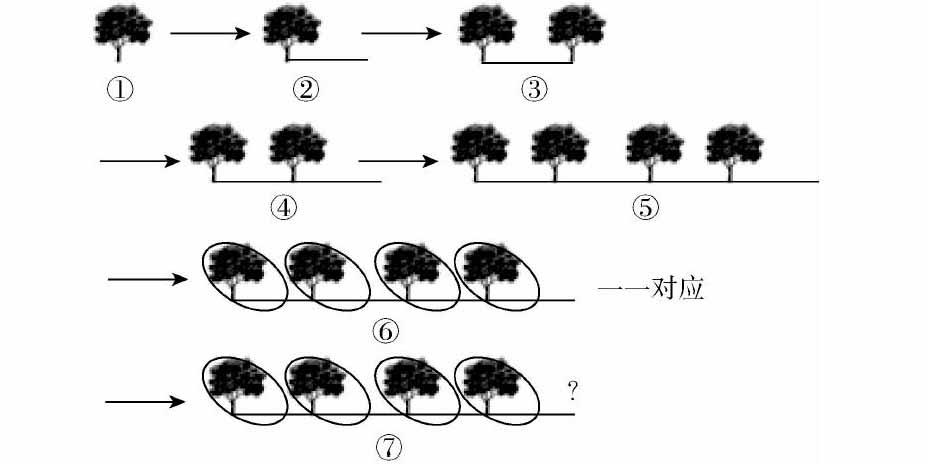
师：现在我在马路的开头种了一棵树，接下来你们觉得要怎样做？（出示①）

生：隔一段距离再种一棵树.

师：也就是说，树的后面要留下一段间隔，对吗？（出示②）接下来呢？

生：再留一段间隔（出示③）;再种一棵树，再留一段间隔（出示④）;再种一棵树，再留一段间隔……（不断地按顺序出现树和间隔，直至出现⑤）

师：同学们，你们有什么发现？

生1：每种一棵树就要留一段间隔.

生2：我觉得树和间隔的数量应该是相等的，一棵树对应一段间隔.

师：总结得太好了，像这样一棵树对应一段间隔（出示⑥），我们把它们的关系称为“一一对应”.（板书：一一对应）

师：种到什么时候停止呢？（出示⑦）

生1：当我们种了一棵树而后面没有路再给我们留间隔时就停止.

生2：种到路的末端就停止.

数学源于生活，学生通过观察图片，讨论如何种树，不断地重复“种一棵树，留一段间隔”，实际上就是在感知发现与“植树问题”相关的这一类问题的本质规律.也就是说学生通过观察“植树问题”相关的信息、明白“植树问题”的要求后归纳推理出树和间隔成一一对应的关系，在这里学生的归纳推理能力得到了发展，为接下来把树和间隔一一对应的关系应用到不同类型的“植树问题”中做铺垫.

二、借助几何直观，深入理解应用规律

在学生的知识构建以及思维发展的过程中，借助几何直观可以让学生深刻体会和理解问题的规律和本质.学生借助画图呈现树与间隔成一一对应关系，可以更深入地理解“植树问题”的规律，帮助学生内化此规律，为后面把树与间隔的关系推广到不同类型的“植树问题”中埋下伏笔.

三、根据实际问题，推广规律完善模型

归纳推理能力在第二学段的教学目标要求学生在观察、实验、猜想等活动中能够进行分析、比较，找出事物的共性和差异，并能形成较完善的结论或模型.在教学过程中，教师需要不断地创设不同的情境，使学生在不同类型的“植树问题”中不断地推广和应用树与间隔成一一对应的规律，从而通过归纳推理构建出数学模型.

【片段二】

师：老师派你们带着21棵树苗到了这条马路边，发现这样的情况，怎么办？

教师出示一端有房子的马路图片.

生1：只需要20棵树.

生2：有一端被房子挡住了，这一端不需要种树，所以要减少一棵.

生3：原来棵数等于间隔数加1，现在再减1，刚好棵数就等于间隔数.

得出结论并计算：

一端栽，一端不栽：棵数=间隔数，100÷5=20（棵）.

师：现在你们把打算栽在首端的树苗还给我了，带着20棵树出发.认真一看，发现这种情况，又该怎么办？

教师出示两端都有房子的马路图片.

生1：再还给老师一棵.

生2：也就是两端都不栽，只需要19棵.

得出结论并计算：

两端都不栽：棵数=间隔数-1.

间隔数：100÷5=20，棵数：20-1=19.

教师创设了不一样的问题情境，出示了一端有房子和两端都有房子的100米长的马路，再问学生要栽几棵树.虽然条件改变了，但是“植树问题”的核心不变，学生仍然可以应用归纳推理得出的树与间隔一一对应的关系解决问题.使学生明白归纳推理得出的结论应用在同一类不同条件的问题中都是成立的.

在整个教学过程中，教师始终引导学生通过归纳推理来完成关于“植树问题”的数学实际问题的探究.在学习过程中，教师通过带领学生观察和分析一系列行道树图片从而归纳推理出树与间隔成一一对应关系，并且通过实际问题把归纳推理得出的结论从“植树问题”推广到与“植树问题”相关的一类问题中.这些教与学的过程，不管是最初的找出规律，后来的应用规律，还是最终的推广规律，都在积极地发展学生的归纳推理思想.只有如此，学生的数学思维才能更好地发展，从而提高数学素养.