立德树人在圆锥曲线教学中的渗透
2020-03-13兰晨曦
兰晨曦


【摘要】通过圆锥曲线的数学美对学生进行美育教育,让学生在学习数学的时候感受其中的美学价值;通过数学在科学技术中的作用培养学生的爱国主义情怀,让学生认识到数学对中华民族的振兴起着举足轻重的作用;通过圆锥曲线内容中展现的辩证思想,让学生学会用辩证唯物主义的眼光看世界.据此来探讨在圆锥曲线的教学中落实立德树人的根本任务的途径.
【关键词】立德树人;圆锥曲线;美育;辩证思想
党的十九大曾提出新时代的教育要落实立德树人这一根本任务,全面发展素质教育.这充分强调了“立德树人”的重要性.要求教师不仅要注重知识和技能的教学,更要充分挖掘数学知识里的思想以及精神.新时代的教师作为“立德树人”的实践者,不仅要注重学生的知识教学,更应该提升教学的育人价值.让学生学会在看待数学时带着“美”的线条,看待世界时带着“数学”的色彩.圆锥曲线作为高中数学最为关键的内容之一,烦琐的知识点较多,对刚接触圆锥曲线的高中生而言,很难建立抽象思维和图形分析能力.传统教学模式熏陶下的教师,通常会让学生直接记住结论或开展题海战术,这种方法对“应试”的结果而言可能很好,但对学生的未来发展以及综合素质的提高是不利的.基于此,本文就圆锥曲线的教学中如何渗透“立德树人”的根本任务进行探讨.
一、感悟数学的美学价值,弘扬中华美育精神
第六届国际数学教育会议提出:“数学教育还必须将数学中所固有的美展示给学生,使学生不仅获得知识,而且还受到美的熏陶.”因此,教师在进行数学教育时,不仅向学生传授知识,更要让学生感悟数学的美学价值,做好美育,在数学的教学中弘扬中华美育精神.
圆锥曲线本身就是一种美,它的概念美、方程美、图形美.所以,在解题时,让学生学会利用圆锥曲线的各种美优化解题,从而降低解题难度,起到事半功倍的效果,还能让学生体会其中所含的美学素养,在数学美的熏陶下发现生活中的美,奠定一种中华美育精神.
例1 双曲线以原点O为中心,其焦点在x轴上,双曲线的两条渐近线l1,l2,过右焦点F作垂直于l1的直线交l1,l2于A,B两点.已知BF
与FA同向,当|OA|,|OB|,|OC|成等差数列时,该双曲线的离心率为多少?
点评 对例1,首先引导学生绘制相关图形(如图1),利用数形结合的思想来分析问题.很大一部分学生直接从定义出发,到后面发现计算极其复杂,很难计算出双曲线的离心率.而对此问题,教师应当进一步引导学生挖掘题干中的条件,让学生通过数形结合自主挖掘出2|AB|=|OA|+|OB|和tan∠AOB=tan2∠AOF这两个条件,同时也是解决此问题最关键的一步,这充分运用了双曲线图形的对称性,找到解决此问题的突破口.
二、体会数学的育人价值,培养学生爱国主义情怀
拿破仑说:“一个国家只有数学蓬勃的发展,才能展现它国力的强大.数学的发展和至善与国家昌盛密切相关.”这表明,数学的研究水平,往往可以决定一个国家和民族的自然科学的研究水平,也决定了国家的科学技术水平,通过具体的实例的展示,让学生从中体会到数学的魅力,从先辈们的伟大成就中培养学生勇于探索、不畏艰难的精神以及强烈的爱国主义情怀.
在圆锥曲线的教学中,让学生观看圆锥曲线的起源以及发展过程,激发学生的学习兴趣,让学生认识到圆锥曲线的重要性.使学生明白数学的发展与科学技术发展息息相关,激励学生为中华民族的振兴努力奋斗.
例2 嫦娥一号的成功发射,为我国探索月球翻开了新的一页.现将嫦娥一号绕月球运行的轨迹看作一个椭圆,月球的位置看作椭圆的一个焦点,当经过月球和嫦娥一号的直线与椭圆的长轴夹角为π2和π3时,嫦娥一号与月球分别相距n万千米和65n万千米,那么嫦娥一号与月球的最远距离为多少?
本题以嫦娥一号为背景,将其转化为椭圆知识,让学生学会用数学解决天文学问题,感受到数学对科学技术发展的重要性,要想祖国更加强大,学好数学是其中一步,从而将爱国主义教育深刻地融入数学教学中.
三、渗透数学辨证思想,树立辩证唯物主义世界观
辩证思想的实质,其实是一种矛盾的客观事物两方面之间的相互转化性和相对统一性.数学作为辩证法的辅助工具和表现形式,在表现辩证法的核心时,不仅提高数学教学质量,而且让学生深刻体会到辩证思想,同时为解决数学问题提供相关的辨证规律.
(一)数形结合,培养对立统一观
数与形的概念是从客观世界得来的,是用来反映客观世界的,而数与形的概念互不相同,两者在形式上相互矛盾,但在一定条件下,又是可以相互转换的.圆锥曲线本身就是数形结合的代表,在教学中,引导学生从数的角度认识圆锥曲线,再从形的角度揭示圆锥曲线的本质.充分利用数形结合将对立的双方统一起来,让学生在学习圆锥曲线的同时,学会建立对立统一的观念.
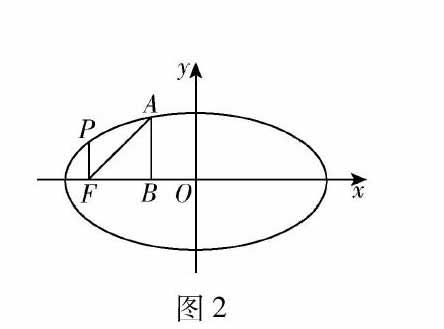
例3 已知标准方程为x24+y23=1的椭圆,直线l过其左焦点F并与椭圆交于A,B两点,满足|AF||BF|=2,求直线l的一般式方程.
(二)动静结合,培养运动变化观
圆锥曲线可以看作是静止的图形,也可以看作是点运动产生的轨迹.因此,在圆锥曲线的教学中,引导学生动手操作,从动的角度发现曲线中的数量关系,再在静止中寻找其中的规律,做到两者互相转化,真正体会“静中有动、动中有静”的辩证关系,在解题中擅于利用这种运动变化的辩证关系,让学生在学习圆锥曲线中培养出运动变化观.
“立德树人”根本任务的落实,具体体现在每一堂课的教学过程中,只有在数学教学中注重知识的传授,同时注重学生世界观,人生观的引导,坚持以德为先的培养理念,“随风潜入夜,润物细无声”,才能培养适应当代社会发展的社会主义建设者与接班人,为实现伟大中国的复兴梦提供合格的人才支撑.
【参考文献】
[1]刘志有.高中数学圆锥曲线教学的有效性策略分析[J].数学教学通讯,2014(15):38-39.
[2]龚彦琴.“美”视角中的圆锥曲线及教育价值[J].数学教学研究,2017(2):10-12.
[3]項素英,洪秀满.浅谈圆锥曲线教学中辩证思维能力的培养[J].中学数学,1995(6):6-9.
