越算越乱的最短路径数

李如

小红帽的外婆住在森林中的一个小村子里，小红帽每个周末都会独自从家出发，前往外婆家看望她，顺便给外婆带上一些美味的食物。狡猾的大灰狼不知从哪里知道了小红帽这个习惯，想要埋伏在路边袭击小红帽，把她抓回去吃掉，还好小红帽的妈妈早有准备。

在小红帽出门之前，妈妈拿了一张从家到外婆家的路线图给小红帽。妈妈嘱咐小红帽，每次从家出发去外婆家的路线都要不同，而且尽量选择较短的路线，这样遇到大灰狼的概率就会大大减少。

“老实”的算法VS“聪明”的算法

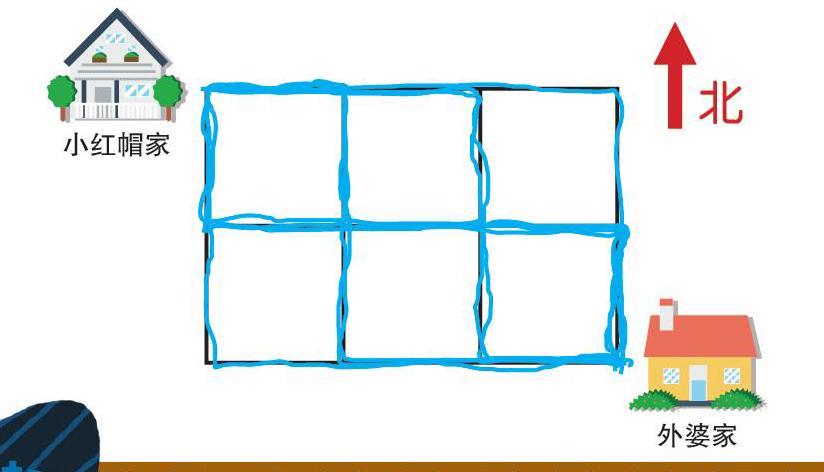
小红帽拿到路线图的时候看了一下，上面给出了所有从自己家到外婆家可以走的小路。因为外婆家在小红帽家的东南方向，所以她要么先向南走，要么先向东走，这样就能顺利到达外婆家。那么，她到底有多少条路线可以选择呢？

小红帽用笔在路线图上将路线一条一条地画了出来，不一会儿，路线图就被弄花了。她数了数，有9条路线可以选择。

妈妈看着小红帽一个人趴在桌子上对着路线图写写画画，便问她：“你在干什么呢？”

“妈妈，我想算一算从咱们家到外婆家一共有几条不同的路线可以选择。”小红帽向妈妈求助，“我一共算出9条，您看看我算得对吗？”

妈妈看着被小红帽弄花的路线图笑了笑：“我教你用另外一种方法来算，保证简单，一学就会！”

“真的吗？快教教我。”小红帽迫不及待地想让妈妈教她另一种计算方法。

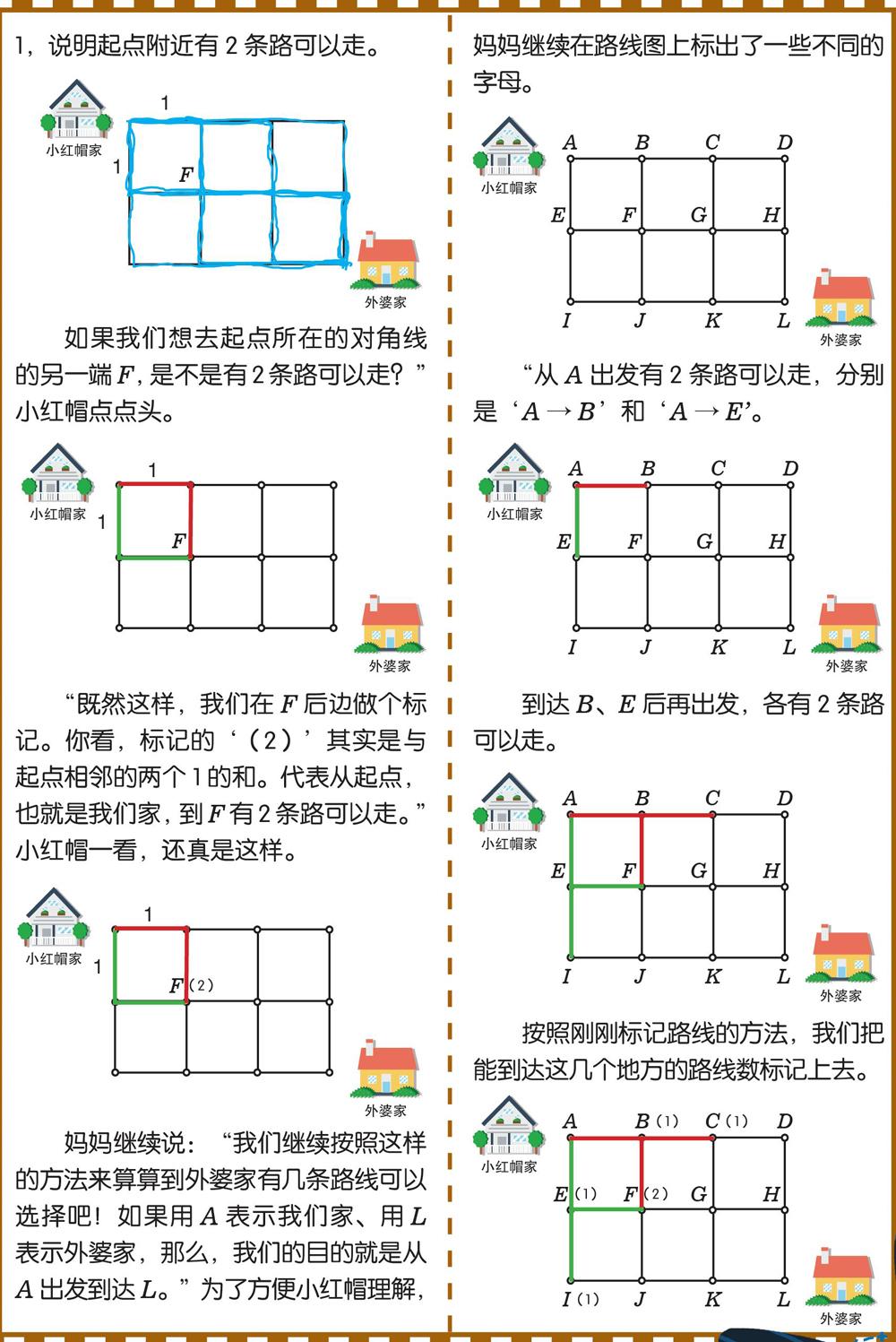
妈妈接过笔，在路线图上标出了数字“1”和“F”，说道：“你看，在与起点相邻的两条道路上分别标上1，说明起点附近有2条路可以走。

如果我们想去起点所在的对角线的另一端F，是不是有2条路可以走？”小红帽点点头。

“既然这样，我们在F后边做个标记。你看，标记的‘（2）其实是与起点相邻的两个1的和。代表从起点，也就是我们家，到F有2条路可以走。”小红帽一看，還真是这样。

妈妈继续说：“我们继续按照这样的方法来算算到外婆家有几条路线可以选择吧！如果用A表示我们家、用L表示外婆家，那么，我们的目的就是从A出发到达L。”为了方便小红帽理解，妈妈继续在路线图上标出了一些不同的字母。

“从A出发有2条路可以走，分别是‘A→B和‘A→E。

到达B、E后再出发，各有2条路可以走。

按照刚刚标记路线的方法，我们把能到达这几个地方的路线数标记上去。

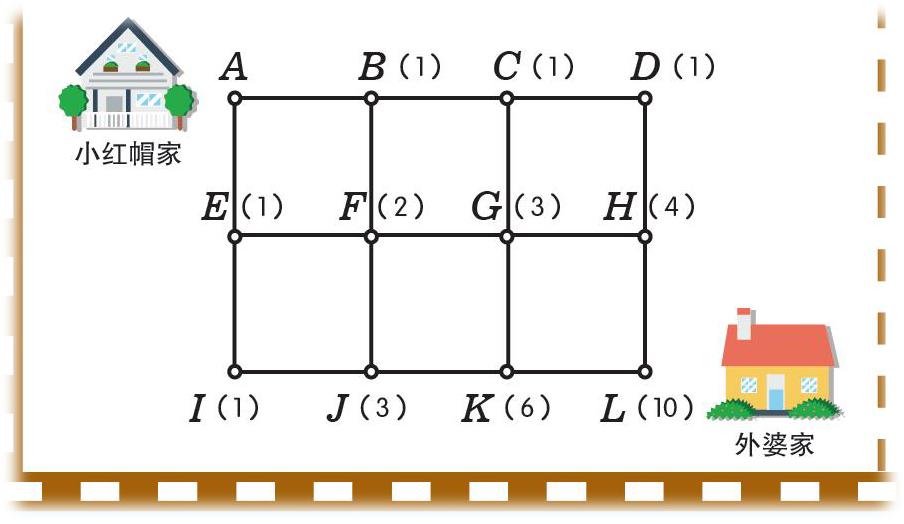
我们不断地按照这个方法画下去，最终就可以得到从A到L的最短路径数。”最后，妈妈在路线图上标出的数是这样的：

“这样算下来，一共有10条路线可以选择呢！之前是我算错了。”小红帽羞愧地说。

妈妈笑了笑：“没关系，你现在学会了这个方法，既可以简便地算出结果，又不会出现遗漏。”

另一种“聪明”的算法

“其实还有另一种‘聪明的计算方法。”妈妈决定多教小红帽一点，“这个方法比上一个方法难一点，你可要开动脑筋，好好思考。”

小红帽立马端正地坐下来：“妈妈您快说。”

“我们先来看看路线图。”

妈妈拿出另一张崭新的路线图，慢慢地画出几条线：“你发现了吗？无论你选择哪条路线，都至少要走3条横向的路和2条竖向的路。”

“实际上，我们只需要确定走的是哪2条竖向的路，就能确定最短路径数。但是这竖向的路不能随便选。”妈妈举了一个例子，“例如，你选择了下边这种路线，就必须要走回头路或者绕远路。”

“对这2条竖向的路的选择还真不能马虎。”小红帽若有所思地说。

妈妈也紧接着说道：“是的，这样的话，我们就要分情况来考虑了。从竖向的路来看，如果我们选择了‘A→E这条路，那么接下来竖向的路，共有4种选择。

如果我们选择了‘A→B→F，那么接下来竖向的路就有3种选择。

如果我们选择了‘A→B→C→G

这条路，接下来竖向的路就有2种选择;最后，如果我们选择‘A→B→C

→D→H这条路，就只剩下‘H→L这1种选择了。”

“把不同情况下的路线数加起来，一共是4+3+2+1=10（条）。”小红帽高兴地说道，“和用第一种方法算出来的结果一样呢！”

妈妈点点头，说道：“在现实生活中，这个路线图的模型算是非常简单的了。今天你学习了新的数学知识，可一定要牢牢记住哟！”