究竟谁的面积更大？

毛玉暄

最近，李老师带着我们一起回顾和复习平面图形面积的相关知识。我突然发现，我们现在学到的、能用公式直接计算面积的图形只有正方形、长方形、平行四边形、三角形、梯形和圆形等规则的几何图形。其他的几何图形，尤其是不规则的图形，或者是所给已知条件较少的图形，都不能套用公式来计算面积，而是需要将其“转化”成我们熟悉的图形。

题目中的两个阴影部分既不是规则的梯形，也不是规则的三角形。但我清楚，计算不规则图形的面积应该试着将其回归到计算规则图形的面积上。让我着急的是题目中的已知条件太少，这个比较麻烦。

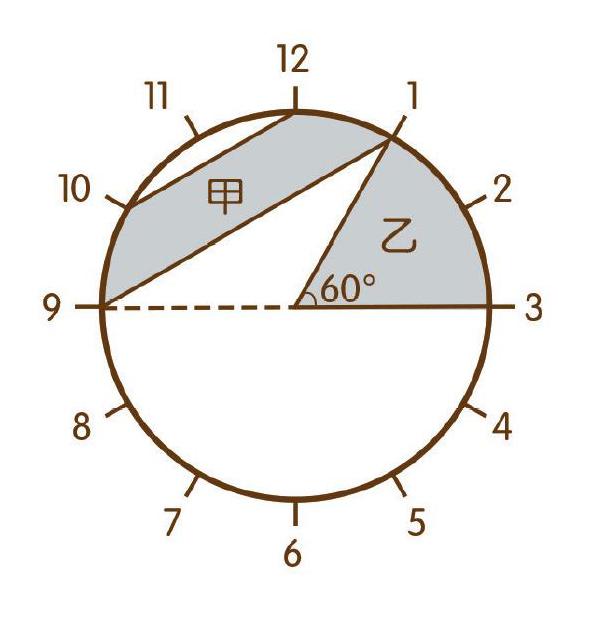
题目只让我们比较两个阴影部分面积的大小，不需要计算结果。于是，我就可以从两个阴影部分与整个圆的关系入手，进行判断。

经过一番观察，我发现：乙是一个扇形，其圆心角是360°÷12×2=60°，所以它的面积是整个圆的面积的1

6。这样一来，只要判定甲的面积占整个圆的面积的几分之几即可。

我想到了利用两个规则图形的面积差来表示甲的面积。甲上方有一块空白的部分（弓形），是不是可以将乙切割下一部分补过去呢？补过去之后，乙的剩余部分就是一个规则的三角形了。

我還发现乙的剩余部分（三角形）和甲下方的空白部分（三角形）都是三角形，并且两个三角形的底都为圆的半径，还共用一条高，说明它们的面积相等。这样，我就可以将乙的剩余部分（三角形）转化为甲下方的空白部分（三角形）。

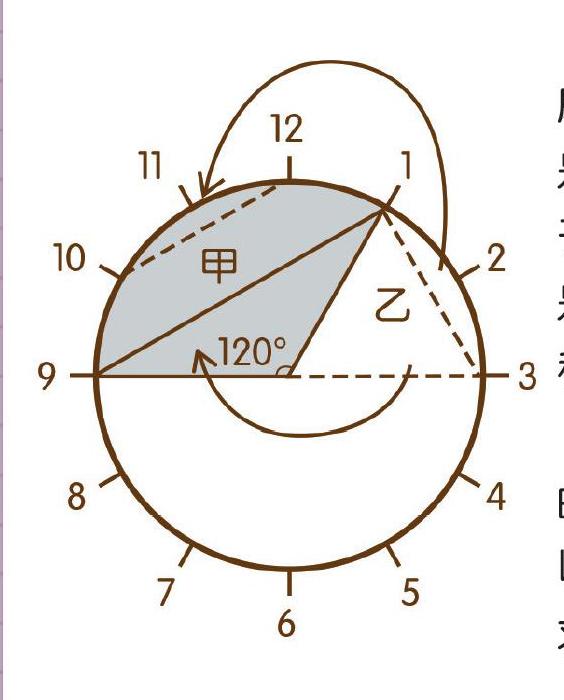
经过这样的操作之后，阴影部分甲与乙的面积合在一起，正好是一个大的扇形的面积。

通过此时的钟面可以看出，这个扇形的圆心角是120°，则它的面积是圆的面积的1

3 。所以，甲的面积等于该扇形的面积减去乙的面积，也就是圆的面积的1

6。所以，甲和乙的面积一样大。

这下，想必大家对求解图形面积的问题有了更好的了解。希望大家在以后的学习中，能善于使用割补法来求解或者比较不规则图形的面积。

指导老师  李小强