螺旋秤工作过程计量误差研究

刘洪海，张鹏飞，张亚刚，郑宗利，汪飞田

（1. 公路建设与养护技术材料及装备交通运输行业研发中心（甘肃路桥建设集团有限公司），甘肃 兰州 730030；2. 长安大学道路施工技术与装备教育部重点实验室，陕西 西安 710064）

螺旋秤是1种集给料、计量于一身，能够进行连续动态给料计量的设备［1］。由于其结构简单、价格低廉、安装方便、便于维修等特点，被广泛应用于化工、建材、电力等众多生产活动中，在沥青混合料搅拌站粉料计量控制方面作用尤为突出。粉料是沥青混合料中的重要组成部分，与沥青结合形成沥青胶浆，填充集料骨架空隙，增大沥青油膜表面积，提高集料与沥青间的结合力。研究表明，粉料用量的多少将直接影响沥青混合料的高、低温稳定性，因此，粉料计量系统的准确性始终是研究热点。孙秉礼［2-3］论述了采用自平衡系统的短螺旋秤和非自平衡系统的长螺旋秤的不足，并提出了相应对策；王世田等人［4］采用螺旋秤对比研究的方法，从秤体结构方面对影响计量精度的因素进行了分析；武玉松等人［5］通过对计量原理的研究，分析得到影响计量精度与稳定性的主要因素，提出水泥计量系统优化方案；王书鹤［6］基于自校正预测算法，提出“先快后慢，最后点动”的新型动态计量控制算法；谭戈［7］通过对计量过程分析，对生石灰螺旋秤零点漂移情况提出解决方法。

已有研究在提高螺旋秤计量精度方面做了大量的工作，但是对螺旋秤工作过程中粉料计量质量与实际质量的误差分析较少。为此，本文依据螺旋秤计量原理，对流量变化过程进行微元化处理，定量分析计量质量与实际质量变化情况，并对两者的误差进行分析，为螺旋计量秤设计和工程应用提供理论依据。

1 螺旋秤工作原理

螺旋秤是粉料供给及计量系统的重要构件［8-12］，通常由恒速电机、螺旋秤秤体、传感器、变送器、控制调节器等组成，图1为螺旋秤供料计量系统简图。

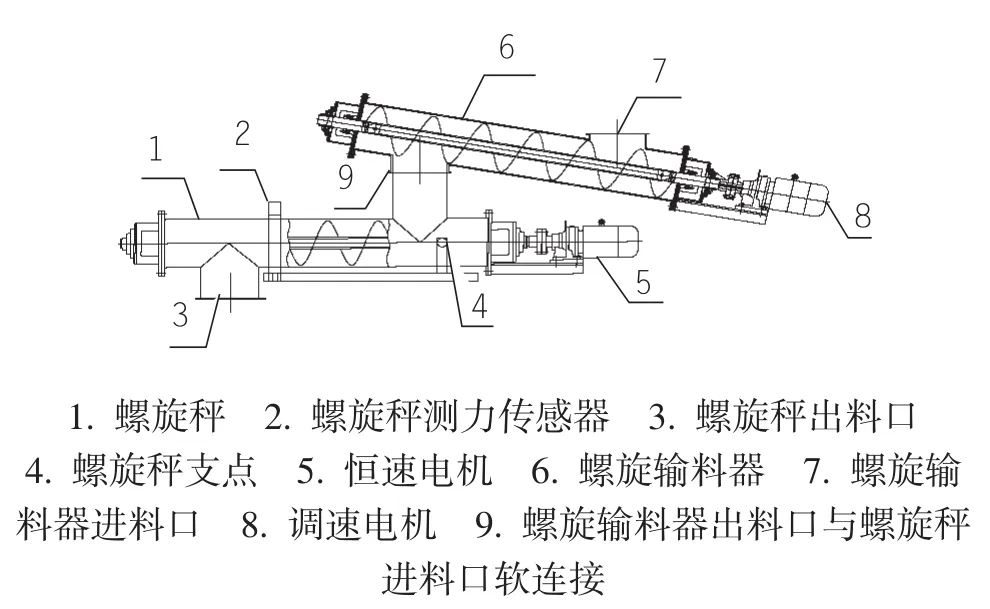
图1 螺旋秤供料计量系统简图

当螺旋秤空载时，由力矩平衡可得

式中：G1为螺旋秤自身重力，N；L1为螺旋秤重心到支点的距离，m；P0为螺旋秤空载时传感器所测拉力，N；L0=为传感器到支点的距离，m。

当螺旋秤内有物料时

式中：G2为螺旋秤内物料的重力，N；L2为螺旋秤内物料重心到支点的距离，m；F为落料冲击作用力，N；L3为物料冲击力作用点到支点的距离，m；P为螺旋秤内有物料时传感器所测拉力，N。

若供料螺旋转速恒定，通常认为物料在螺旋秤内均匀分布［13-15］，取螺旋秤进出料口中心距离的1/2作为物料重心到支点的距离，即L2=L/2。

联合式（1）（2）可得

由于螺旋秤在设计过程中，为减小物料冲击对计量结果的影响，理论上冲击力F的作用点与支点重合［16］，即，因此式可转换为

式中：ΔP为螺旋秤正常工作与空载时传感器所测拉力的差值，N；M为物料质量，kg；g为重力加速度，m/s2；L为螺旋秤进出料口中心距离，m。

由于粉料填充系数、螺旋秤间隙及瞬时电压波动等多方面因素影响，粉料计量质量并不是一成不变的［17-18］。当系统检测到质量超出设定范围后，通过控制调节器改变螺旋输料器转速实现对粉料供给量的调节［19-20］，其工作流程如图2所示。

图2 粉料计量控制系统工作流程

2 调节过程波动性与误差分析

假设某段调节过程中螺旋秤内粉料分布如图3所示。

图3 螺旋秤内粉料分布简图

取螺旋秤任意一点处的微元段进行分析，根据力矩平衡可得

式中：Q为供料螺旋流量，kg/s；v为粉料在螺旋秤内水平移动速度，m/s；l为料流颗粒距离进料口中心距离，m；t为料流颗粒在螺旋秤内移动l所用时间，s；T为料流颗粒在螺旋秤内移动时长，s。

设供料螺旋流量变化为Q=a+bsin（ωt+φ），代入式（7）可得出螺旋秤计量质量：

式中：a为供料螺旋流量均值，kg/s；b为供料螺旋流量变化幅值，kg/s；ω为供料螺旋流量变化角速度，rad/s；φ为初相位，rad。

此时，螺旋秤内粉料实际质量为：

由此可知，调节过程中螺旋秤计量误差为

由式（7）、（9）可知，当流量为某一定值时，粉料计量质量与实际质量相等；当流量发生变化时，计量质量与实际质量存在误差。由式（11）可知，计量质量与实际质量误差与供料螺旋流量均值a、供料流量变化幅值b、供料流量变化角速度ω、料流颗粒在螺旋秤内移动时长T以及初相位φ有关。由式（11）还可看出，计量质量与实际质量误差与供料螺旋流量均值a负相关，流量均值越大，误差越小；与供料流量变化幅值b正相关，变化幅值越大，误差越大。因此，在运行过程中为减小计量误差，应提高供料流量均值，保持连续稳定供料，且控制流量变化幅值在一定范围内。

为了分析供料螺旋流量变化角速度ω对计量误差的影响，以GX250型螺旋输料机为例，赋值a=8.3kg，b=0.1a，设供料螺旋流量变化角速度ω分别取不同的值5rad/s，10rad/s，15rad/s，20rad/s，依次令料流颗粒在螺旋秤内移动时长T为1s、2s、3s、…、50s；借助MATLAB软件绘图可得到不同角速度下最大误差δmax（δmax=max（|δ|））随T变化的关系曲线，见图4所示。为方便研究，对曲线进行包络线处理，见图5所示。为了分析初相位φ对计量误差的影响，设初相位φ分别取不同的值0rad、2rad、4rad、6rad，依次令料流颗粒在螺旋秤内移动时长T为1s、2s、3s、…、50s，可得到不同变化幅值下最大误差δmax随T变化的关系曲线，见图6所示。

由图4可知，当供料螺旋的流量变化角速度一定时，最大计量误差随料流颗粒在螺旋秤内移动时长增加而减小，并存在特征点；当移动时长小于该点时，最大误差随移动时长的减小快速增加；当移动时长大于该点时，最大误差随移动时长的增大缓慢降低。由图5还可看出，该特征点与螺旋流量变化角速度负相关，角速度越大其值越小。当供料流量变化角速度为5～20rad/s时，料流颗粒在螺旋秤内移动时长（即螺旋秤长度与料流在螺旋秤内移动的水平速度的比值）在8～4s较为合理。由图6可知，最大误差δmax受初相位影响较小。

图4 不同角速度下最大误差δmax随T变化的关系曲线

图5 不同角速度下最大误差δmax随T变化的包络线

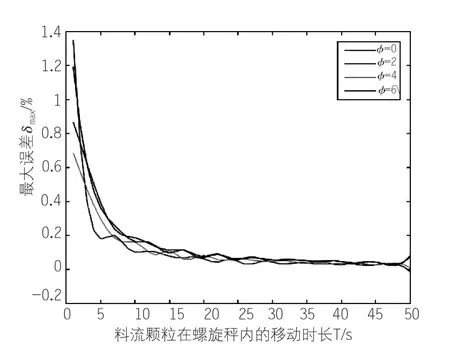
图6 不同初相位下最大误差δmax随T变化的关系曲线

3 结束语

依据螺旋秤的计量原理，建立工作过程计量误差模型，通过分析可得到如下结论：

（1）螺旋秤配料过程中，计量质量与实际质量存在误差，对于供料螺旋流量变化角速度为5～20rad/s而言，当料流颗粒在螺旋秤内移动时长小于8～4s时，螺旋秤计量质量与实际质量最大误差变化明显；当料流颗粒在螺旋秤内移动时长大于8～4s时，变化较为平缓；因此，在供料螺旋流量变化角速度为5～20rad/s时，螺旋秤长度与料流在螺旋秤内移动速度的比值宜为8～4s；

（2）计量误差与供料螺旋流量均值负相关，流量均值越大，误差越小；与供料流量变化幅值正相关，变化幅值越大，误差越大。因此，在运行过程中为减小计量误差，应提高供料流量均值，并保持连续稳定供料，且控制流量变化幅值。