结合粒子滤波与卡尔曼滤波的RSSI室内定位算法
2020-03-13陈军慧
冯 帆,吴 春,陈军慧
(中电海康集团有限公司,浙江 杭州 310012)
0 引言
物联网(Internet of Things,IOT)技术的发展,使得室内定位技术获得广泛关注,而在室内环境中,全球导航卫星系统(Global Navigation Satellite System,GNSS)的定位信号微弱,不能用于室内定位,由此衍生出GNSS之外的室内定位技术。
对于室内定位技术,根据距离可将其分为测距法和非测距法,其中基于非测距法包括:质心算法[1]、APIT算 法 (Approximate Point-in-triangulation Test)[2]、位置指纹匹配算法[3]等;基于测距的常用方法包括:三角定位算法,最小二乘定位算法,基于信号到达角度(Angle of Arrival,AoA)[4]、信号达到时间(Time of Arrival,ToA)[5]、信号到达时间差(Time Difference of Arrival,TDoA)[6]、信号强度RSSI(Received Signal Strength Indicator)的定位[7]算法等。
由于基于测距的定位精度一般要比基于非测距的定位精度高,实际应用往往采用基于测距的定位算法。考虑到基于RSSI测距无需精确的时间同步和角度测量,也不需要增加额外设备,功耗成本低且实施简单,更加适用于室内定位系统,所以本文采取基于RSSI的定位技术来预估室内待测节点的位置,同时结合粒子滤波与卡尔曼滤波,来提高定位精度。
1 算法模型
本文基于RSSI定位模型的流程图如图1所示。
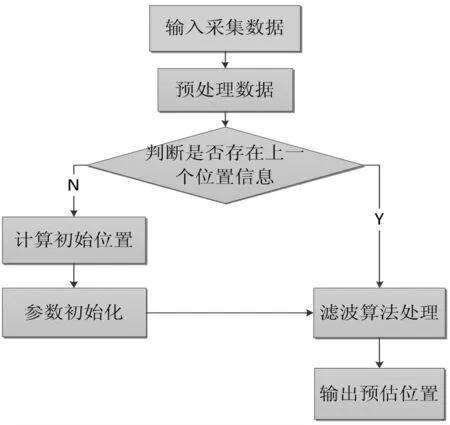
图1 RSSI定位算法流程图Fig.1 Algorithm flow chart of RSSI localization
在利用RSSI进行定位之前,首先需要建立基于RSSI测距的模型,即信号强度RSSI和距离d的关系。
1.1 模型建立
理论上,无线信号和距离存在一定关系。若在已知发射节点和接收节点功率的情况下,可根据理论或经验传播模型把传播损耗转换为距离。传统的无线信号传播衰减模型为[8]:
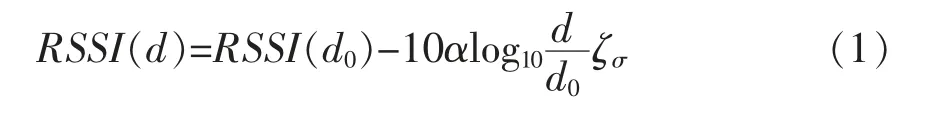
其中:RSSI(d)表示距离发射节点为d的接收节点接收到的信号强度;α表示信号传播过程中的损耗因子;ζσ表示标准差为σ的服从正态分布的随机量。一般情况下,为简化模型,令d0=0,即距离为1m时的信号强度,且不考虑影响较小的ζσ,则简化后的模型为:

根据简化后的信号衰减模型,对测量的RSSI和d进行对数拟合,得到常系数A=RSSI(1)和α,从而就可确定RSSI和d的关系。
1.2 数据预处理
基于RSSI测距的模型,就可以在已知RSSI的情况下,根据:

计算得出标签与信标的距离,从而就能够对标签进行定位。
对于处于静止状态的标签,对标签接收到的RSSI做高斯滤波处理;而对于移动状态下的标签,标签位置会发生变化,标签接收到的RSSI也不是同一位置的值。如果对移动标签接收到的RSSI采用常用的滤波方法,如:均值滤波、中值滤波、高斯滤波处理等,得到的结果并不具有参考价值。标签在移动时,由于当前位置和前一位置存在某种关系,采用速度常量滤波[9]处理标签在某一时间段内接收到的RSSI值,并利用滤波后的值对标签进行位置预估。
对于某个标签接收到的所有RSSI数据{ri}in=1,采用速度常量滤波进行处理,该滤波过程有两个阶段:

其中:riprev为i时刻RSSI的测量值,ripred为i时刻RSSI的预测值,riest为i时刻RSSI的预估值,vipred为i时刻RSSI变化率的预测值,viest为i时刻RSSI变化率的预估值;a,b为增益值,为采样时间间隔。
1.3 结合粒子滤波位和卡尔曼滤波的定位算法
结合粒子滤波(Particle Filter,PF)用于目标追踪的思想,将粒子滤波用于室内移动标签定位,以标签的位置坐标为状态值,接收到的RSSI值为观测值,其具体过程如下:
(1)初始状态:根据初始位置估计,对初始位置增加随机扰动,得到粒子的初始位置;
(2)预测阶段:根据标签移动规则以及粒子前一位置信息,预测粒子当前的位置;
(3)校正阶段:对每个粒子的预测位置进行评估,越接近于实际观测值的粒子权重越大;
(4)重采样:根据粒子权重对粒子进行筛选,筛选过程中,既要大量保留权重大的粒子,又要有一小部分权重小的粒子;
(5)滤波:将重采样后的粒子作为新的粒子,并取其位置均值作为当前预估位置,转步骤2。
考虑到标签在移动过程中前一位置和后一位置之间存在线性关系,采用线性卡尔曼滤波(Kalman Filter,KF)对粒子滤波的结果进行优化。以标签位置坐标和速度为状态值,以粒子滤波预估位置为观测值,则卡尔曼滤波的迭代方程为:
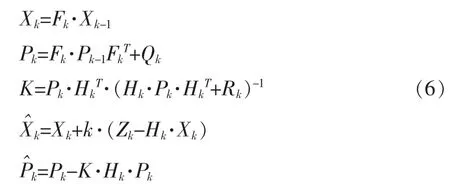
其中,Xk=(xk,yk,vxk,vyk)为k时刻的状态值,表示k时刻的预估位置和预估速度;


2 仿真实验和结果分析
测试环境为某个办公室,标签置于高度约2.5m的天花板,测试人员佩戴标签在室内移动。设置标签发包频率为1s/3次,移动状态下的标签每2s计算一次位置。
2.1 基于RSSI测距
考虑到测试人员佩戴标签在移动的过程中会出现面对信标、背对信标、侧对信标等各种情况,在测量RSSI和距离关系的时候,分别采集了测试人员在面对和背对信标的两种情况下接收到的RSSI值。
由于RSSI值浮动较大,在每种情况下的每个位置均采集了2min的数据。对于采集的2min数据,采用高斯滤波处理方式得到当前位置所对应的RSSI,最后将面对和背对情况下处理后的RSSI值取均值,结果见表1。

表1 RSSI以及对应的距离dTable 1 RSSI and its corresponding distance d
根据RSSI和距离d的关系:

可知,RSSI和距离d的对数成线性关系。因此,对RSSI和log10d做线性拟合,拟合参数见表2。

表2 线性拟合参数Table 2 Parameters of linear fitting
从而得到A=-57.51α=2.24。将系数重新代回式(7),得到RSSI和距离的关系式,其拟合曲线如图2所示。

图2 RSSI和距离拟合曲线Fig.2 Fitting curve of RSSI and distance
在获得RSSI和距离的关系之后,开始测试预估标签在不同状态(静止和移动)下的室内位置。测试环境主要在办公室四楼,安装在办公室的信标的位置示意如图3所示,各个信标的坐标见表3。
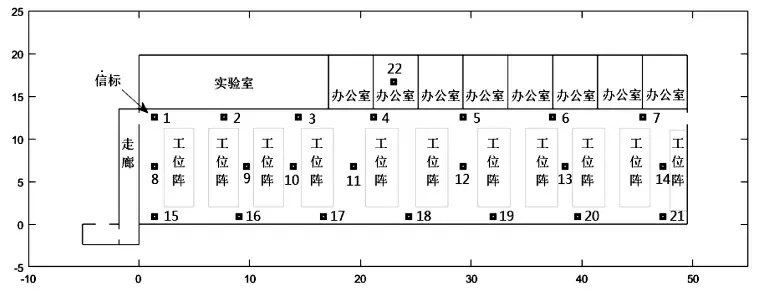
图3 信标安装位置示意图Fig.3 Position schematic diagram of installed beacons
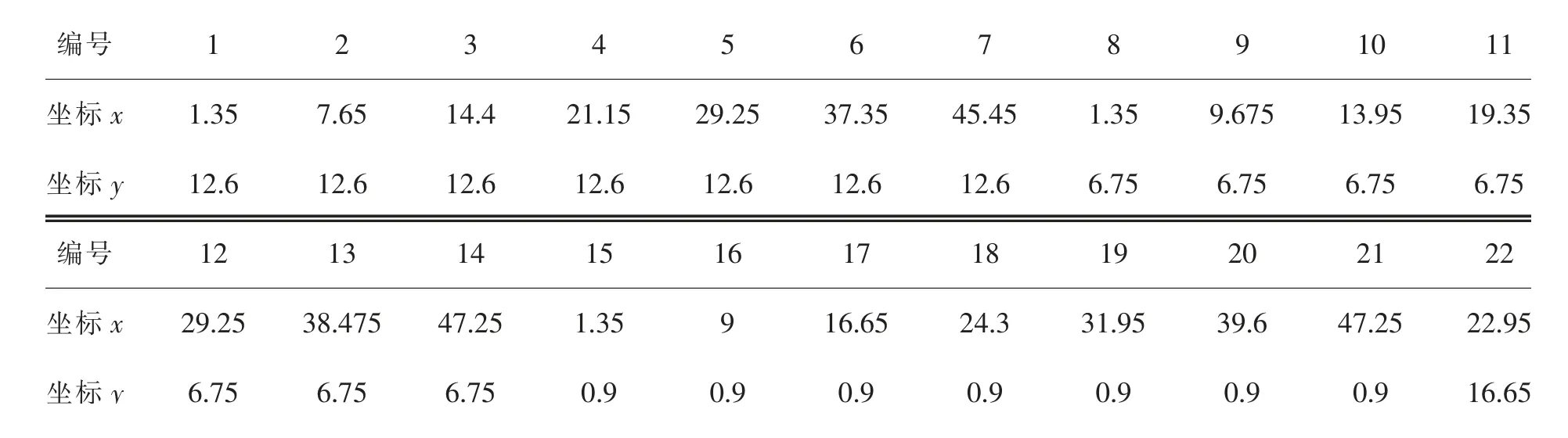
表3 信标坐标Table 3 Positions of beacons
2.2 预估标签位置
2.2.1 静止标签定位
将标签置于某工位上,收集信标发出的信号一定时间后,对该段时间内收集到的RSSI做高斯滤波处理,然后采用本文提出的滤波算法进行位置预估,得到的预估结果如图4所示。
在图4中,实心五角星点为标签真实位置,空心五角星为该段时间内预估的标签位置。以标签真实位置为圆心,分别作半径为3m,4m和5m的圆,可以发现采用本算法预估的标签位置基本均在4m圆的范围内,大多数落在2m圈内。将标签固定在某一位置进行多次测试,分别计算预估位置落在2m圈、3m圈、4m圈以及5m圈内的概率;同时,与传统质心法、丁恩杰等人[10]提出的基于距离的加权质心算法的定位精度概率进行了对比,结果见表4。
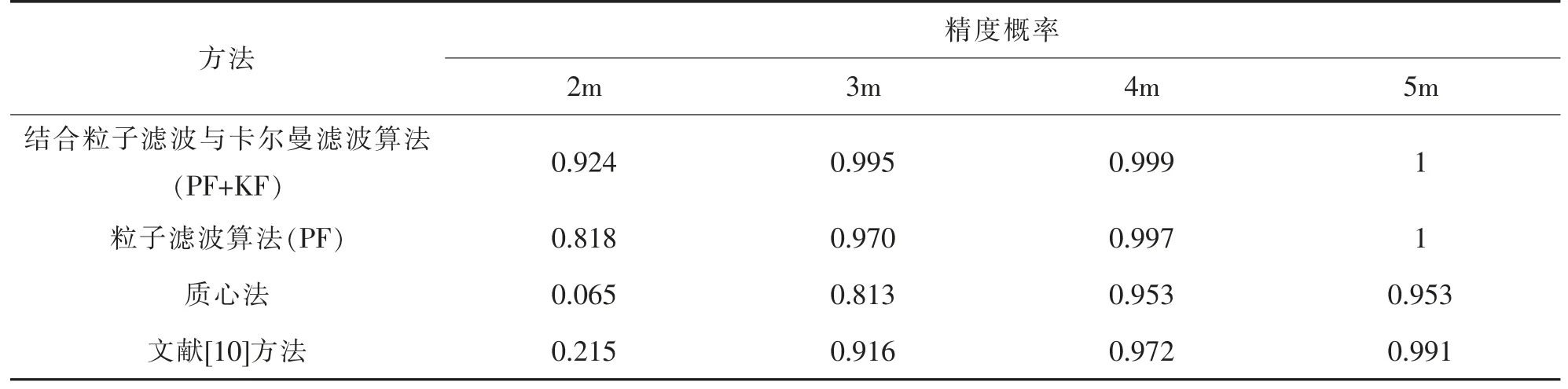
表4 不同算法的预估位置精度概率对比Table 4 Comparison of estimated position accuracy probability of different algorithms

图4 静止于某位置的标签定位结果图Fig.4 Positioning results of a tag in a certain position
2.2.2 移动标签定位
测试人员将标签以佩戴工作牌的方式佩戴在胸前,在布置信标区域内匀速运动,测试结果如图5所示。

图5 待定位目标移动轨迹示意图Fig.5 Moving track of a target to be localized
图5中实心五角星表示本文算法预估的位置,从小标号到大标号为测试人员移动方向,其中存在部分预估位置重合的情况,比如13和14,16和17,35和36等,出现这种情况是由于标签当前接收到的RSSI信号较弱。测试结果显示,预估的移动轨迹与测试人员实际行走路径一致,且满足定位误差要求。
3 结语
本文研究了基于RSSI的室内定位算法,首先采用粒子滤波预估标签位置,然后利用卡尔曼滤波对标签的预估位置进行优化。对于静止状态下的标签,采用高斯滤波处理RSSI;对于移动状态的标签采用速度常量滤波处理,最后均采用以上方法进行定位。
在室内场景进行实际测试,结果表明本文提出的定位方法能够达到低于3m的定位精度的概率为99.5%,而且能够实现对移动标签的实时定位。
