最大相关系数预测模型在热电厂短期热负荷预测中的应用

姜 平，赵保国，石晶晶，张海伟，王 琦，杨超杰

(1.山西河坡发电有限责任公司，山西 阳泉 045001；2.山西大学 自动化系，太原 030013)

0 引言

热电厂短期负荷预测对热电厂水资源的节约和城市化集中精确供热有着至关重要的作用，精确的负荷预测可以提高城市供热的精确度，还可以节约成本和节约资源，为可持续发展提供有效方案。热负荷预测需要预测出电厂的供回水温度以及供水流量，根据热负荷计算公式得到预测的热负荷值，利用该结果进行热负荷控制，避免了热负荷在实际的测量中存在较大延时造成的供热滞后的问题。短期负荷一般波动比较大，采用传统的预测方法[6-8]比较困难，而且预测精准度不高。神经网络预测和模糊预测虽然在短期负荷预测有比较好的效果，但训练样本大，收敛速度慢，外推性比较差，对于需要实时预测数据来进行现场设备的快速优化控制时往往存在很大问题。神经网络短期负荷预测需要考虑的影响因素众多，其中包括：供回水温度差、供回水流量差、供回水压力、环境气温、锅炉侧一二次风的风量、含氧量等，这些数据在预测前的数据选择优化比较复杂，并且在预测过程中容易陷入局部最优，造成预测样本的选择和训练周期过长，无法做到实时预测。此外，在当前的热电厂的DCS控制系统中，无法用现有的逻辑功能块搭建神经网络预测模型，只能通过外挂方式实现数据的导入，造成控制的麻烦和不稳定性。最大相关系数预测法采用的方法为通过计算待预测组和不同影响因素数据之间的相关系数，选取出和待预测组相关系数最大的数据组，利用该组已知数据对待预测组进行短期预测。采用相关系数最大组进行短期负荷预测，能够极大简化预测过程，预测速度快，而且外推性好，能够采用电厂DCS现有的功能块搭建预测模型，可以及时发现预测过程中的问题所在，为实时控制需求提供可靠方案。

1 最大相关系数预测模型建立

确定最大相关系数组，需要计算不同影响因素组和待预测组之间相关系数。通过计算出前n项不同数据和待预测组的相关系数，取绝对值后选择绝对值最大所对应的影响因素数据组作为之后预测的参考数据，进行下一步的短期预测。

最大相关系数预测模型建立分六个步骤。

(1)计算前n项不同影响因素数据和待预测组之间相关系数[9-10]，计算方法参考公式(1)。

(1)

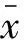
通过上述的相关系数计算公式，可以得到不同的相关数据组和待预测组数据的前n项的相关系数为βn(A,B),βn(A,C),βn(A,D)，…。其中A为待预测组；B，C，D为相关数据组；

(2)将所求的相关系数取绝对值，得到|βn(A,B)|,|βn(A,C)|,|βn(A,D)|，…；

(2)

(3)求相关系数绝对值中最大值ρ=max[|βn(A,B)|,|βn(A,C)|,|βn(A,D)|，…]；

(3)

(4)选取相关系数绝对值中最大值ρ所对应的数据组η作为预测模型,进行下一步的预测，预测计算公式如公式(4)所示。

(4)

(5)如果所求的相关系数绝对值|α1|，|α2|，|α3|，…中，存在大小几乎一致的情况，则采用以下方法进行负荷预测：

假设和待预测组最大相关系数有两组，分别为B，C组，则按照B，C两组数据和A组数据前n项的相关系数的比例按占比进行分配，通过相关系数的占比进行A组数据下一步的预测，具体预测公式如公式5所示。

(5)

式中，α1为A，B组数据前n项相关系数；α2为A，C组数据前n项相关系数。

为了保证预测结果的实时可靠性以及最大相关系数组选择的准确性，对最大相关系数计算需要定期重新运算，具体计算选择方法如公式(1)-(5)所示；

(6)求预测误差ε和相对误差σ。

误差为：

ε=n+i-an+i.

相对误差为:

(6)

根据预测误差的结果，对原有的数据组进行误差修正，使预测相关样本更加精确，为下一步最大相关系数预测提供可靠数据。

2 最大相关系数预测模型实际应用

2.1 最大相关系数预测结果图像分析

为了验证该预测模型效果，本文引入图像分析法进行预测效果分析，如图1某热电厂热网回水温度预测效果对比和图2某热电厂热网供水流量预测效果对比。

由图1对比可知，某热电厂供热回水温度预测值和实际值基本吻合，最大误差控制在4.5 ℃以内，后期有部分误差增大是由于采取建模样本较少造成的[10-12]，增加预测模型构建样本可有效解决误差问题，该预测过程相比于神经网络预测简单，计算速度快[13-15]，能够满足实时控制的需求。

预测所得热电厂的供热供水流量在实际供热供水流量上下波动，且误差不大，和实际的供水流量的拟合度较高，可以作为短期负荷预测模型。

2.2 最大相关系数预测结果误差分析

为进一步验证本预测方法的准确度，对预测结果的回水温度预测误差和供水流量误差取绝对值，并进行分析，如图3和图4所示。

由图3可知，预测回水温度和实际回水温度误差绝对值平均维持在2～3 ℃之间，最大在4.5 ℃以内，符合短期负荷预测的精度需求[16-18]，且该预测方法收敛速度快，外推性好，适合短期负荷预测。

由图4可知，预测供水流量和实际供水流量误差绝对值平均维持在50 t/h～60 t/h，满足流量预测实时控制的需求，该预测结果表明该预测方法在供水流量预测和控制中有一定实用价值。

2.3 预测热负荷的计算

根据热负荷的计算公式，结合本预测的回水温度和实际的实时供水温度求偏差，该结果与实时供水流量带入热负荷计算公式，即可得到实时的热负荷，计算公式如下：

Q=CMΔt.

M=hρ.

式中，Q为实时热负荷数据，kJ/h；C为水的比热容常数，即4.2 kJ/(kg·K)；M为供水质量，kg;Δt为供回水温度差；h为供水流量，kg/h;ρ为水密度。

3 结论

最大相关系数法利用不同影响因素和待预测数据之间的相关系数的最大组进行短期预测，仅需要相邻2～3天的数据作为预测样本进行相关系数运算，得到与待预测组之间相关系数最大的影响因素数列，利用该组数据带入预测计算公式进行预测待预测组之后一两天的数据，该过程建模简单，预测过程快速，精准度较高[19-20]。预测结果表明，该方法的回水温度预测误差控制在4.5 ℃以内，供水流量预测误差平均维持在50 t/h～60 t/h以内，适合数据样本不大，且外推性要求高的短期负荷预测。在实际的负荷预测中能够及时根据该预测模型判断出异常数据组并进行修正，有一定的实用价值。