对分组密码算法ARIA算法不可能差分分析的改进
2020-03-13欧海文王湘南李艳俊雷亚超
欧海文 王湘南 李艳俊 雷亚超
1(北京电子科技学院信息安全系 北京 100070)2(西安电子科技大学通信工程学院 陕西 西安 710071)
0 引 言
ARIA算法[1]由韩国学者设计,从开始的ARIA 0.8版、ARIA 1.0版和ARIA 1.2版,确定最终版本为1.2版。ARIA算法是分组长度为128 bit的SPN型的分组密码[2],密钥长度支持:128 bit、192 bit和256 bit,迭代轮数分别为12、14、16轮[3]。采用了与AES算法[4]相似的结构,很多AES算法的分析方法也适用于ARIA,结合ARIA算法的研究,实现了对ARIA算法的不可能差分攻击。
不可能差分分析是由Knudsen和Biham分别独立提出[5-6]。与差分不同,不可能差分分析的理念是凭借概率为0的差分特征,将那些会导致概率为0的差分出现的候选密钥去除,因为若使用正确的密钥来对明文进行加密,不可能得到这样的密文差分特征[3]。筛除这些候选密钥值,剩下的就是正确的密钥值。
1 ARIA算法
1.1 ARIA算法介绍
ARIA是分组长度为128 bit的SPN型密码,ARIA每一轮由3个部件构成:
1) 轮密钥加(RKA)。由每一轮的输入状态和轮密钥ki两者之间按字节进行异或构成,而轮密钥ki是由密钥扩展算法得到的。
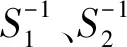
SLo=S1S2S1-1S2-1S1S2S1-1S2-1S1S2S1-1S2-1S1S2S1-1S2-1
SLe=S1-1S2-1S1S2S1-1S2-1S1S2S1-1S2-1S1S2S1-1S2-1S1S2
SLo、SLe分别在单数轮中用和在双数轮中用。
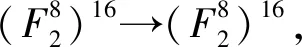
y0=x3⊕x4⊕x6⊕x8⊕x9⊕x13⊕x14y1=x2⊕x5⊕x7⊕x8⊕x9⊕x12⊕x15y2=x1⊕x4⊕x6⊕x10⊕x11⊕x12⊕x15y3=x0⊕x5⊕x7⊕x10⊕x11⊕x13⊕x14y4=x0⊕x2⊕x5⊕x8⊕x11⊕x14⊕x15y5=x1⊕x3⊕x4⊕x9⊕x10⊕x14⊕x15y6=x0⊕x2⊕x7⊕x9⊕x10⊕x12⊕x13y7=x1⊕x3⊕x6⊕x8⊕x11⊕x12⊕x13y8=x0⊕x1⊕x4⊕x7⊕x10⊕x13⊕x15y9=x0⊕x1⊕x5⊕x6⊕x11⊕x12⊕x14y10=x2⊕x3⊕x5⊕x6⊕x8⊕x13⊕x15y11=x2⊕x3⊕x4⊕x7⊕x9⊕x12⊕x14y12=x1⊕x2⊕x6⊕x7⊕x9⊕x11⊕x12y13=x0⊕x3⊕x6⊕x7⊕x8⊕x10⊕x13y14=x0⊕x3⊕x4⊕x5⊕x9⊕x11⊕x14y15=x1⊕x2⊕x4⊕x5⊕x8⊕x10⊕x15
1.2 符号说明
本文使用的符号及标注如表1所示。

表1 使用的符号及标注
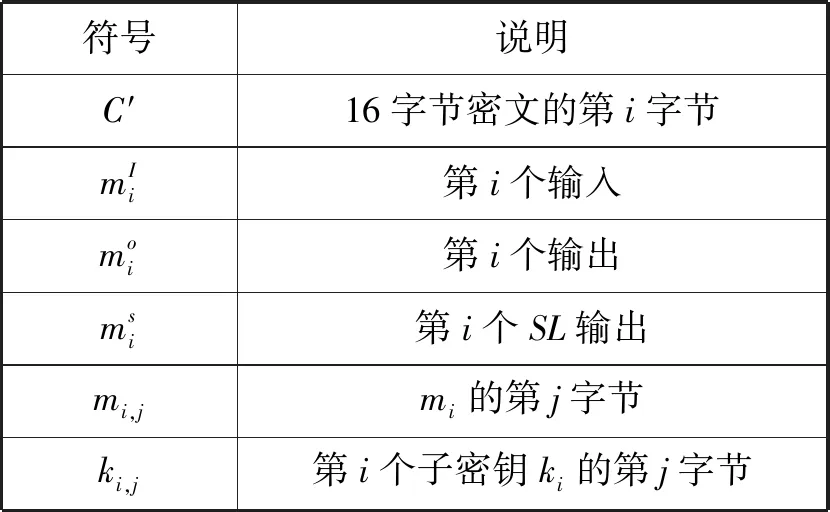
续表1
2 对7轮ARIA-256的不可能差分分析
在Yu Sasaki和Yosuke Todo给出的4轮不可能差分区分器上添加2轮前置路径、1轮后置路径,得到7轮不可能差分路径。
2.1 ARIA算法的2个性质
性质1如图1所示,存在一差分对,在字节(1,4)处差分值非0,其余字节处差分值为0,4轮变换后,ΔX4的差分特征不会是如下式子:
(h⊕g,0,0,0,h⊕g,h,h,0,0,h,0,0,0,g,0,g)
这一不可能差分性质可用下式表示:
(0,a,0,0,a,0,0,0,0,0,0,0,0,0,0,0)→/
(h⊕g,0,0,0,h⊕g,h,h,0,0,h,0,0,0,g,0,g)
式中:a、h和g为任意非零值。
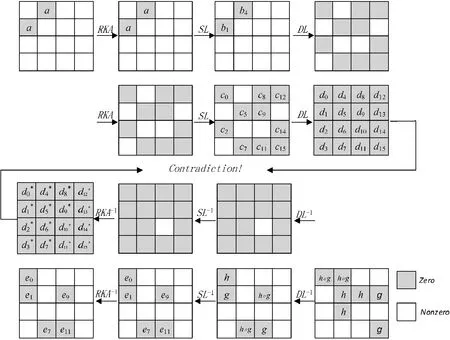
图1 ARIA算法的4轮不可能差分
证明:首先从前两轮正推。
明文对的输入状态满足(0,a,0,0,a,0,0,0,0,0,0,0,0,0,0,0),经过第一轮RKA运算后,由于RKA运算不改变差分,所以差分没有发生改变,经过第一轮SL运算,差分特征为:
(0,b1,0,0,b4,0,0,0,0,0,0,0,0,0,0,0)
其中:b1和b4为非0字节。经过第一轮DL运算,差分特征为:
(b4,0,b1⊕b4,0,0,b1⊕b4,0,b1,b1⊕b4,b1,0,b4,b1,0,b4,b1⊕b4)
再进行RKA运算和SL运算,差分特征为:
(c0,0,c2,0,0,c5,0,c7,c8,c9,0,c11,c12,0,c14,c15)
然后进行第二轮的DL运算,差分特征为:
(d0,d1,d2,d3,d4,d5,d6,d7,d8,d9,d10,d11,d12,d13,d14,d15)
其中:d10=d15=c2⊕c5⊕c8⊕c15。
再推导(h⊕g,0,0,0,h⊕g,h,h,0,0,h,0,0,0,g,0,g)经过两轮逆变换。经过1次DL-1运算,差分特征为:
(h,g,0,0,0,0,0,h⊕g,0,h⊕g,0,g,0,0,0,0)
经过SL-1、RKA-1运算,差分特征为:
(e0,e1,0,0,0,0,0,e7,0,e9,0,e11,0,0,0,0)
再进行1次DL-1运算,差分特征为:
(e9,e7⊕e9,e1⊕e11,e0⊕e7⊕e11,e0⊕e11,e1⊕e9,e0⊕e7⊕e9,e1⊕e11,e0⊕e1⊕e7,e0⊕e1⊕e11,0,e7⊕e9,e1⊕e7⊕e9⊕e11,e0⊕e7,e0⊕e9⊕e11,e1)
其中:e0、e1、e7、e9、e11为非0值。
最后经过SL-1运算和RKA-1运算,差分特征为:
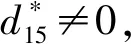
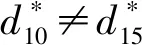
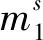
p0=p5=n9+n14
(1)
p2=p7=n11+n12
(2)
p8=p13=n0+n7
(3)
p3⊕p6⊕p9⊕p11⊕p12⊕p14=0
(4)
p0⊕p1⊕p2⊕p4⊕p8=0
(5)
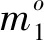
同理,式(2)和式(3)都成立。
又有:
p0=n9+n14p1=n7+n9+n12p2=n11+n12p3=n0+n7+n11+n14p4=n0+n11+n14p6=n0+n7+n9+n12p8=n0+n7p9=n0+n11+n12+n14p11=n7+n9+n12+n14p12=n7+n9+n11+n12p14=n0+n9+n11+n14
所以,式(4)和式(5)成立。
p=248/272=2-24
证毕。
2.2 7轮ARIA的不可能差分攻击过程
上述7轮不可能差分路径如图2所示。其中ARIA算法的最后一轮的扩散层由密钥加替换。在分析时间复杂度时采用了密钥恢复的“early-abort”(早夭)技术[7]。

图2 7轮ARIA的不可能差分路径
攻击过程如下:

步骤2取2N个上述结构,选取密文对中在(1,2,3,7,8,10,11,12,14)这9个字节处差分为0,剩余密文对有2N+223×2-8×(16-7)=2N+151个。
步骤3猜测密钥k8的7 B(k8,0,k8,4,k8,5,k8,6,k8,9,k8,13,k8,15),假设步骤2中保留下来的密文对为(C,C′)。在计算复杂度时,只需要计算7 B的值的复杂度。
步骤3.1猜测密钥(k8,5,k8,6,k8,9),计算:

步骤3.2猜测密钥(k8,13,k8,15),计算:
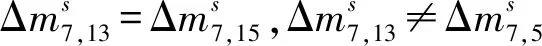
步骤3.3猜测密钥(k8,0,k8,4),计算:

步骤4猜测密钥k1的14个字节,并结合性质2分析,使保留下来的密文对相应的明文对为(P,P′)。计算复杂度时,因为只有密钥加和扩散层操作,所以进行每一次运算就相当于2/3的1轮运算。
步骤4.1猜测密钥(k1,0,k1,5),计算:
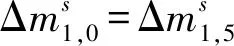
步骤4.2猜测密钥(k1,2,k1,7),计算:
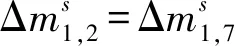
步骤4.3猜测密钥(k1,8,k1,13),计算:
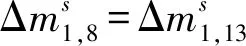
步骤4.4猜测密钥(k1,3,k1,6,k1,9,k1,11,k1,12,k1,14),计算:
步骤4.5猜测密钥(k1,1,k1,4),计算:
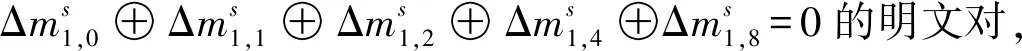
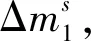
步骤5猜测密钥(k2,0,k2,7,k2,9,k2,11,k2,12,k2,14),计算:
所以总的攻击时间复杂度为:
(3×2164+2173+2180+1/3×2158+1/3×2166+1/3×2174+2214+1/3×2222+1/3×2216+15×2205)×1/7≈2217
综上所述,7轮的攻击复杂度为2112数据复杂度和大约2217次7轮加密运算。
3 8轮ARIA算法的不可能差分分析
在4轮不可能差分区分器上添加了2轮前置路径和2轮后置路径,形成8轮ARIA算法的不可能差分路径,如图3所示。
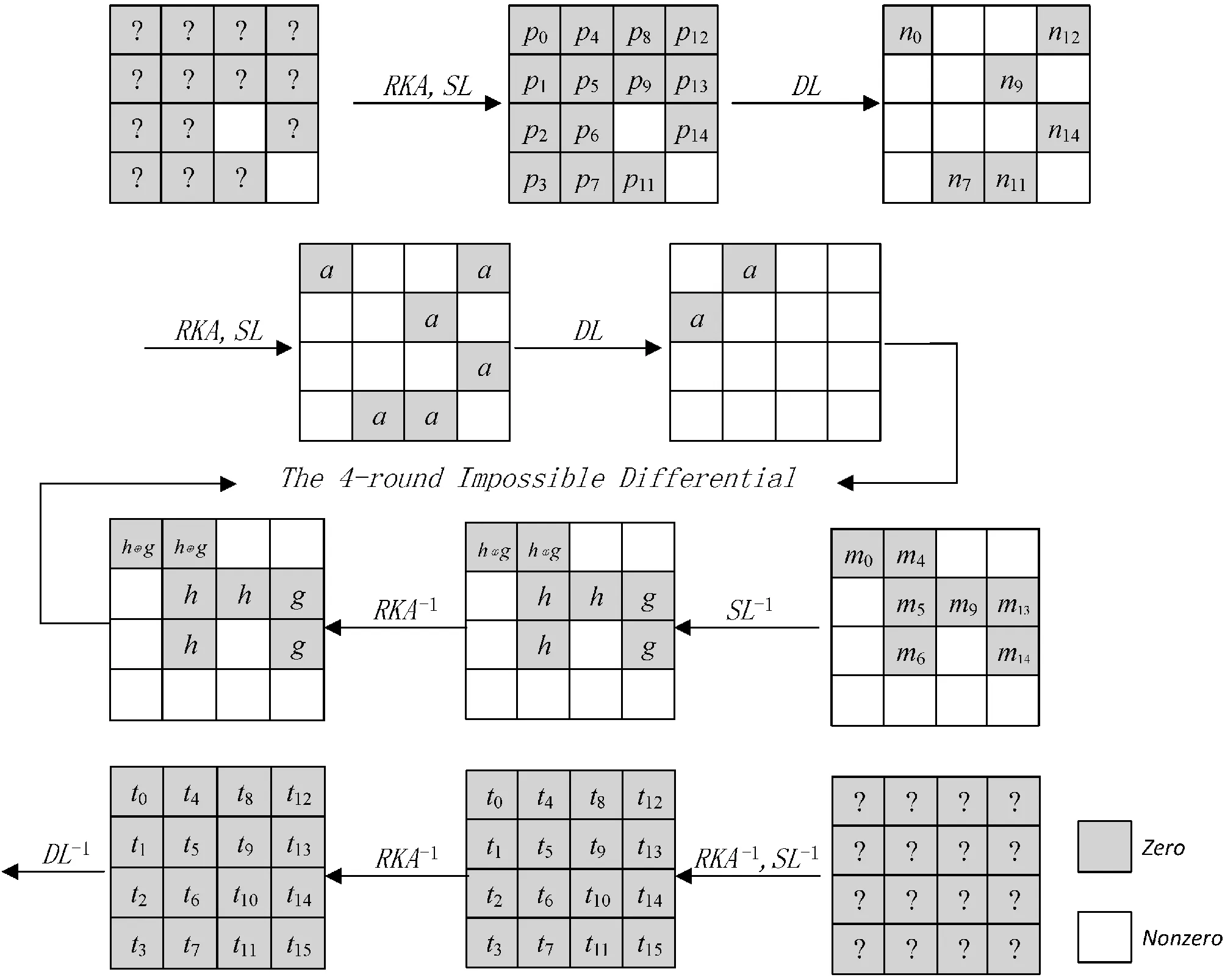
图3 8轮ARIA的不可能差分路径
3.1 ARIA算法的另一性质
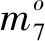
t2⊕t5⊕t12=0
(6)
t1⊕t11⊕t15=0
(7)
t4⊕t10⊕t13=0
(8)
t5⊕t6⊕t8=0
(9)
t0⊕t7⊕t11=0
(10)
t3⊕t9⊕t15=0
(11)
t4⊕t5⊕t14=0
(12)
证明同性质2类似,这里省略。
3.2 8轮ARIA的不可能差分攻击过程
8轮不可能差分分析路径中,ARIA算法的最后一轮的扩散层由密钥加替换。
攻击过程如下:

步骤2取2N个上述结构,这样明文对有2223×2N=2N+223对。
步骤3猜测密钥字节(k9,0,k9,1,k9,2,k9,3,k9,4,k9,5,k9,6,k9,7,k9,8,k9,9,k9,10,k9,11,k9,12,k9,13,k9,14,k9,15)对步骤2中留下来的任意密文对(C,C′),分别进行以下计算:
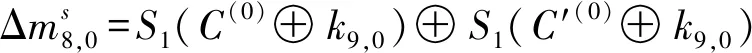
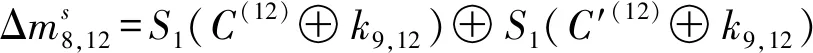
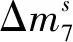
步骤4猜测k8的16 B,并利用性质3进行分析。在步骤4中计算复杂度时,因为只有RKA和SL这两种操作,我们把每次操作可当作2/3的1轮操作。
步骤4.1猜测(k8,2,k8,5,k8,12),并计算:
选择满足t2⊕t5⊕t12=0的密文对,剩余2N+103×2-8=2N+95个密文对。这一步骤需要232×2×2182×224×3/16×2/3=2236次1轮加密运算。
步骤4.2猜测(k8,1,k8,11,k8,15),并计算:
选择满足t1⊕t11⊕t15=0的密文对,剩余2N+95×2-8=2N+87个密文对。这一步骤需要232×2×224×2174×224×3/16×2/3=2255次1轮加密运算。
步骤4.3猜测(k8,4,k8,10,k8,13),并计算:
选择满足t4⊕t10⊕t13=0的密文对,剩余2N+87×2-8=2N+79个密文对。这一步骤需要232×2×248×2166×224×3/16×2/3=2268次1轮加密运算。
步骤4.4猜测(k8,6,k8,8),并计算:
选择满足t5⊕t6⊕t8=0的密文对,剩余2N+79×2-8=2N+71个密文对。这一步骤需要232×2×272×2158×216×2/16×2/3=1/3×2277次1轮加密运算。
步骤4.5猜测(k8,0,k8,7),并计算:
选择满足t0⊕t7⊕t11=0的密文对,剩余2N+71×2-8=2N+63个密文对。这一步骤需要232×2×288×2150×216×2/16×2/3=1/3×2285次1轮加密运算。
步骤4.6猜测(k8,3,k8,9),并计算:
选择满足t3⊕t9⊕t15=0的密文对,剩余2N+63×2-8=2N+55个密文对。这一步骤需要232×2×2104×2142×216×2/16×2/3=1/3×2293次1轮加密运算。
步骤4.7猜测(k8,14),并计算:
选择满足t4⊕t5⊕t14=0的密文对,剩余2N+55×2-8=2N+47个密文对。这一步骤需要232×2×2120×2134×28×1/16×2/3=1/3×2292次1轮加密运算。

步骤5猜测密钥k1的14 B,并结合性质2进行分析,使对应的明文对为(P,P′)。在步骤5中,只有RKA和SL这两种操作,我们把每次操作可认为是2/3的1轮操作。
步骤5.1猜测(k1,0,k1,5),计算:
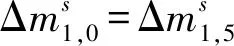
步骤5.2猜测密钥(k1,2,k1,7),计算:
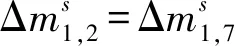
步骤5.3猜测密钥(k1,8,k1,13),计算:
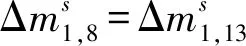
步骤5.4猜测密钥(k1,3,k1,6,k1,9,k1,11,k1,12,k1,14),计算:
步骤5.5猜测密钥(k1,1,k1,4),计算:
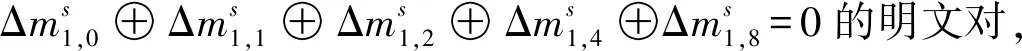
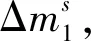
步骤6猜测密钥(k2,0,k2,7,k2,9,k2,11,k2,12,k2,14),计算:

总的攻击时间复杂度为:
(15×2319+2236+2255+2268+1/3×2277+1/3×2285+1/3×2293+1/3×2292+1/3×2287+1/3×2157+1/3×2165+1/3×2173+2213+1/3×2221+1/3×2215+15×2204)×1/8≈2319
综上所述,8轮的攻击复杂度为2191数据复杂度和大约2319次8轮加密运算。
4 改进的不可能差分分析
本文还改进了文献[12]的7轮分析和8轮分析,使用的4轮不可能差分如图4所示。
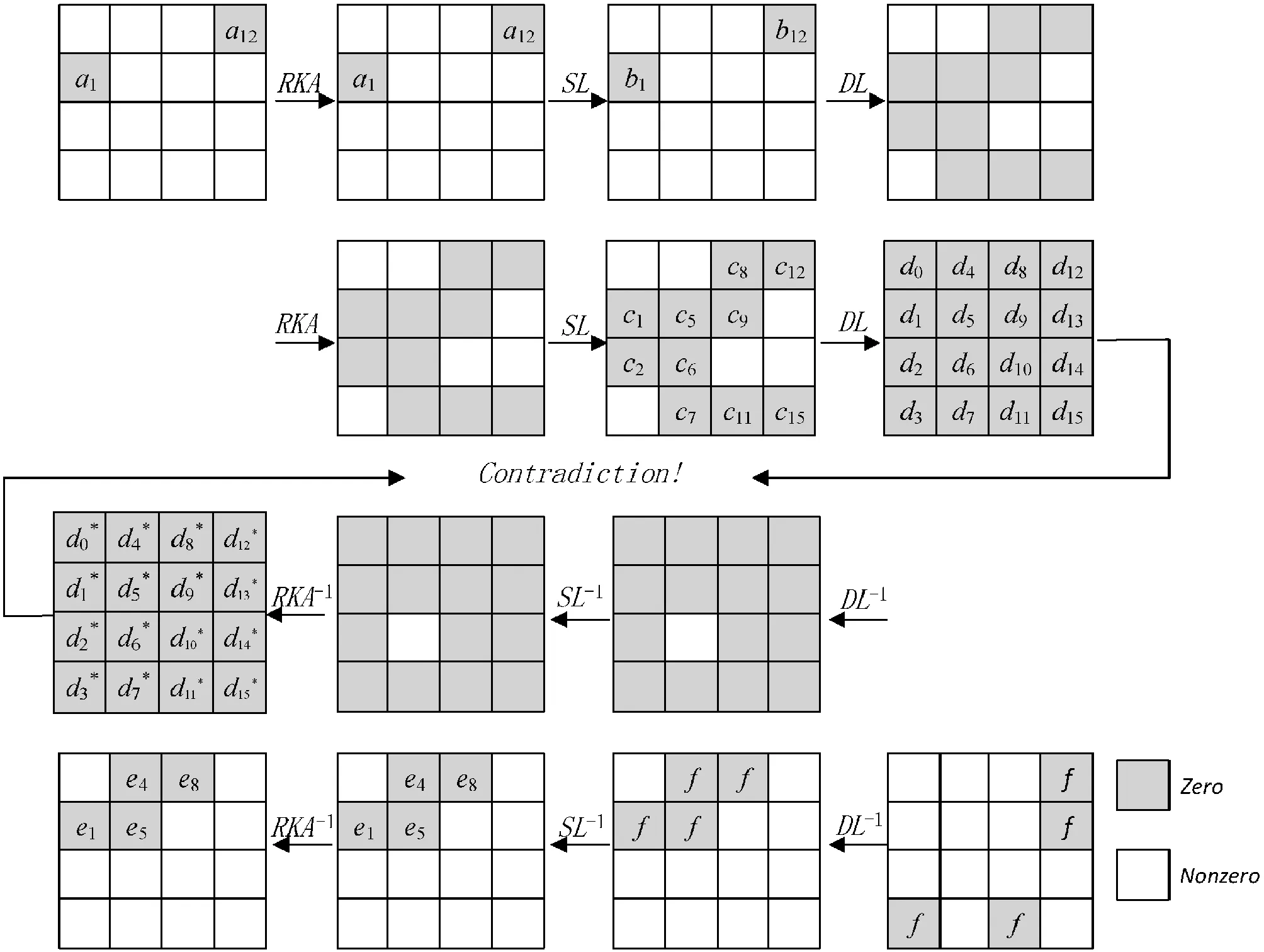
图4 四轮不可能差分
c0=c13=b6⊕b8
(13)
c3=c14=b5⊕b11
(14)
c5=c8=b1⊕b15
(15)
c2⊕c4⊕c7⊕c9⊕c10⊕c15=0
(16)
c0⊕c1⊕c3⊕c5⊕c12=0
(17)
证明同性质2类似,这里省略。
性质2中符号具体代表含义详见参考文献[12],这里不再赘述。
对于7轮攻击,结合性质4,进行密钥恢复,需要的攻击复杂度为:2112+2N=2112+7=2119数据复杂度和大约2216次7轮加密运算。
对于8轮分析,使用性质4的同时,将步骤4.1的DL操作,放到步骤4的最后一步,需要数据复杂度2112+295=2112+95=2207和大约2327次8轮加密运算,进一步减少了时间复杂度。
5 结 语
本文在Yu Sasaki和Yosuke Todo给出的4轮不可能差分的基础上,依据ARIA算法的结构特征,添加了2轮前置路径和1轮后置路径,实现了7轮ARIA算法的不可能差分分析。此路径下,7轮分析共需要数据复杂度为2112和时间复杂度为2217次7轮加密运算。实现了ARIA算法的8轮不可能差分分析,在4轮不可能差分上添加了2轮前置路径和2轮后置路径。在该路径下,8轮分析共需要时间复杂度为2191和大约2319次8轮加密运算。最后还改进了文献[12]的分析结果,与原结果相比较,降低了时间复杂度。不同算法的不可能差分对比结果如表2所示。
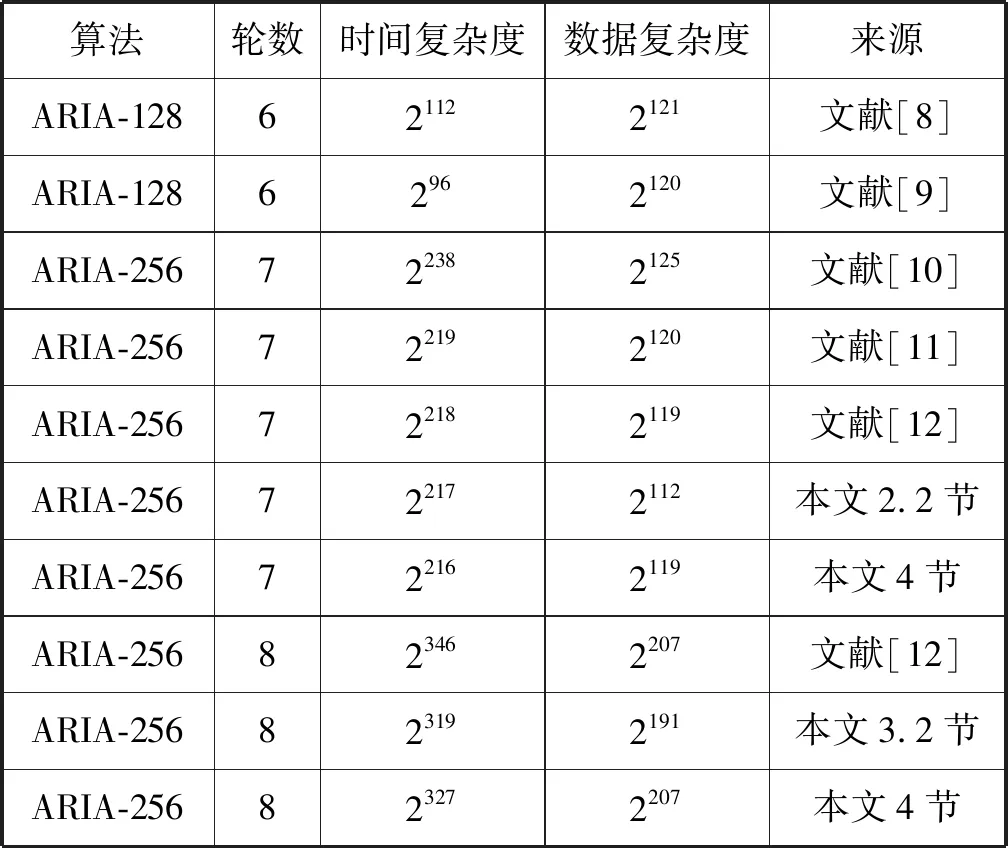
表2 ARIA算法的不可能差分总结
未来研究的重点在于寻找新的不可能差分区分器,再尝试用不同的密钥恢复技术来降低8轮ARIA
算法不可能差分分析的复杂度,使得其时间复杂度低于穷举搜索的攻击复杂度。
