高校扩招政策降低了城镇劳动力的大学教育溢价吗？——基于反事实选择的因果关系推断

方 超，黄 斌

（南京财经大学公共管理学院，江苏南京210023）

一、问题的提出

高校扩招政策是我国现存争议最大的教育制度之一。高等教育毛入学率在扩招政策的带动下，由20世纪90年代的3.5%上升到了新千年的12.5%，在2018年更是达到了48.1%（教育部，2019）。扩招政策将我国高等教育由精英化推向普及化的同时，也为劳动力市场供给了一批具有大学及以上受教育程度的劳动力，经济活动人口中技能型劳动力的占比由扩招前期的2.9%上升到了扩招后期的19.4%（国家统计局，2018）。

有关资本-技能互补与过度教育的研究表明，大学扩招对劳动者收入的影响存在着两种机制[1-2]。第一种机制：大学扩招后，技能型劳动力比重上升并占据了非技能型劳动力的工作岗位，大学文凭与岗位的“错置”造成了大学教育收益率的下降，但非技能型劳动力的工资溢价却相对稳定，故扩招缩小了由人力资本因素引致的期初收入差距。第二种机制：技能型劳动力的供给扩张，但技能偏态型技术进步却刺激了资本市场的投入，促使厂商通过较低的市价购入新技术，技术市场的扩大又推动了劳动力市场对技能型劳动力的有效需求，大学教育溢价的提高也扩大了不同教育层级间的期初收入差距。针对高校扩招、技能型劳动力的过度供给以及教育收益率变动间的不确定性，本研究旨在利用微观计量的因果推断方法，测度城镇劳动力的教育收益率与大学教育溢价水平，深入讨论大学教育是否相对于高中阶段教育而言，仍然是一项高效的人力资本投资形式。研究结果一方面为增强城镇劳动力的资源配置效率、缩小城镇劳动力组内收入差距提供扩招层面的经验证据，另一方面也为我国高等教育在后大众化时期更加注重公平发展提供可参考的决策依据。

二、既有文献回顾

自明瑟提出人力资本收益函数后，学界便在明瑟方程的基础上，利用不同类型的数据形式，采用不同计量方法，实证检验教育扩展、大学教育对劳动力收入水平的影响，一方面旨在实现教育与收入的因果关系推断，另一方面亦可为高等教育政策评估与反思提供量化指导。譬如，萨卡罗普洛斯（Psacharopoulos，2004、2018）[3-4]的研究横向比较了不同经济发展阶段、教育层级与教育回报率的相互关系，发现发达经济体的教育回报率相对较低，并且初等、高等以及高中教育收益率呈递减趋势。克罗伊斯和多基耶（De la Croix&Docquier，2007）[5]针对美、法两国的比较研究，利用大学教育的参与率作为代理指标，发现高等教育大众化虽然促进了两国劳动力的人力资本积累，但高等教育收益率的下降却是不争的事实。然而，阿西莫格鲁（Acemoglu，2011）[6]却在研究中得出相反的结论，即美国大学教育溢价自20世纪80年代起便不断上升，但教育扩张在除英国外的欧洲大多数国家却抑制了工资的增长[7]。肯亚瑟拉（Kenayathulla，2013）[8]新近的研究基于马来西亚劳动力市场的收入数据，发现大学教育回报率高于初等教育但却低于高中阶段教育。

随着扩招政策的深入，高等教育收益率及其变动趋势愈发引起我国学者的关注。李实、丁赛（2003）[9]的早期研究揭示了城镇劳动力的大学教育回报率自20世纪90年代以来的不断上升势头。张车伟（2006）[10]基于抽样调查的数据研究，发现初中及以下、高中及以上受教育程度的教育回报率分别为2.75%和5.9%，而大专及以上受教育程度的估计值却不显著，因而不能说明大学教育相较于高中教育更有利于个体增收。丁小浩等（2012）[11]利用入户调查统计数据的研究，发现除初中教育以外，城镇居民的各级教育回报率呈现出下降的趋势，其中大学与研究生教育的净收益分别由2002年的24.95%与50.55%下降到了2009年的23.67%与35.40%。陈纯槿（2012）[12]的研究利用倾向得分匹配法，检验了扩招前后高等教育收益率的变动，发现扩招政策并未使得全体劳动力均质获益，预期选择与收入机制决定了扩招政策有限的受益者。

新近的研究在研究视角上更加注重对扩招政策的绩效评价，试图通过大学教育回报率的变化判断扩招政策对劳动力个体增收的影响。譬如，刘泽云（2015）[13]利用CHIP数据的研究，采用工具变量法（IV）与赫克曼两阶段样本选择模型解决了内生性与自选择偏差后，指出大学教育愈发能够形成对人的增值，并在此基础上聚焦于大学教育质量对劳动力收入状态的潜在影响，发现大学教育质量对收入存在正向影响，而劳动力的比较优势则是个体是否进入“211”大学的决定因素（刘泽云、邱牧远，2017）[14]。方超、黄斌（2018）[15]新近的研究则发现，高校扩招并未通过大学教育质量下降从而抑制城镇劳动力的大学教育回报率。

总的来说，既有研究已经围绕高校扩招政策做了大量扎实有益的研究工作，并且在提高教育分配的公平、缩小收入差距以及推进高等教育内涵式发展等方面提出了卓有成效的政策建议，但仍然存在可供研究的留白。第一，在研究设计上，既有研究基于高等教育收益率的变动趋势，通过横向比较评价了扩招政策对劳动力收入变化的影响，但缺乏比对教育层级上的纵向差距，即未能将扩招政策实施前后的高等教育收益与高中阶段教育（普通高中与职业高中）收益进行纵向对比，因而在评价大学教育对人的增值影响时，可能有失全面性。第二，在研究方法上，教育回报率的相关研究往往面临着反事实选择、样本选择与遗漏变量等计量问题的掣肘[16-17]，但相关研究大多聚焦于一种或两种计量偏差，因而在测度大学教育回报时，增加了系数偏估的风险。

三、研究设计

（一）模型与方法

借鉴经典明瑟收入方程，利用普通最小二乘法（Ordinary Least Squares，OLS）估计城镇劳动力的整体教育收益率与大学教育的处理效应：

本文将采用普通最小二乘法、分教育层级回归、工具变量法以及赫克曼两阶段样本选择模型估计式（1），并将教育回报率与大学教育回报率作为基准回归的估计结果。

（二）大学教育的处理效应

基准回归的研究假设为教育选择的同质性，但罗伊（Roy，1951）[18]、威尔斯和罗森（Wills&Rosen，1979）[19]等学者的研究却指出，劳动力在做出某一层级的教育选择时是异质而非同质的，因而同质性的教育回报率便可能导致异质性偏估（Heckman&Li，2004）[20]。具体说来，城镇劳动力根据个体偏好，在高中阶段教育后做出进一步的教育决策。该决策包含两种类型的行为选择（此处不考虑既不进入劳动力市场也不接受大学教育的个体选择）：一种选择是直接进入劳动力市场，凭借高中教育取得工资收入；另一种选择是进入大学继续深造，寄希望于通过大学教育获得更高水平的收入，但必须支付当期货币成本与机会成本。无论个体做出何种教育选择，均是以自身的比较优势并结合成本-收益分析所做出的判断，认为能够从大学教育中收获更多回报的个体，更倾向于接受大学教育，因而大学参与率便高于那些认为可能获益较少的个体，但这一决策并非随机过程。

教育选择的异质性使得教育回报对个体增收的影响也具有异质性。对劳动者而言，同为教育年限的增长，但大学教育层级在理论上要比高中阶段教育有着更强的个体增收效应。此时，明瑟收入方程中的教育年限便很清晰地区分出两种学历教育下的教育年限增长对劳动者收入的精确影响。对于教育选择的异质性，传统处理方法是在式（1）的基础上，根据教育选择建立二元哑变量。当时，表示城镇劳动力做出第二种教育选择，即接受大学教育表示高中阶段教育后直接进劳动力市场。则为高中阶段或大学教育的个体增收效应。

根据 Heckman（2001）[21]的研究，我们将大学教育的处理效应表述为下列三种形式：

第一，城镇劳动力做出大学教育选择并接受大学教育后的收入水平为，在高中阶段教育后直接进入劳动力市场的收入水平为，X为影响收入水平的一组矢量。那么，大学教育相对于高中阶段的增收效应（ATE）便可表述为：

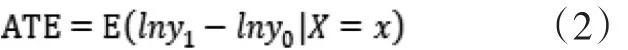
第二，大学教育的处理效应为（ATT）：

第三，高中阶段教育的处理效应为（ATU）：

如果个体的大学教育决策为随机过程，那么处理组（接受大学教育）与参照组（未接受大学教育）下的劳动力便具有了相同的个体、家庭、区域等特征，而仅存在受教育程度的差别，我们可以将参照组的收入水平作为处理组的收入反事实数据，通过OLS即可得到无偏的处理效应。但是，教育决策并非随机生成，而是基于个体比较优势和成本-收益的判断。事实上，接受大学教育的个体通常对未来收益有着较高的认知。因此，基于微观数据的经验研究便很难满足随机试验的需要。

（三）倾向得分匹配与大学教育的处理效应

为纠正异质性的教育选择引致的偏估，我们将采用倾向得分匹配的准实验研究设计，估计大学教育的处理效应。具体做法是：借鉴罗森鲍姆和鲁滨（Rosenbaum&Rubin，1985）[22]提供的研究思路，根据个体教育选择建立二值Probit模型，即其中，X为影响教育选择的控制变量。首先，估计城镇劳动力做出大学教育选择的概率值；其次，将大学教育的处理组与高中阶段教育的参照组按照倾向得分相近的原则进行匹配，在数据平衡的基础上估计大学教育的平均处理效应，并通过对比大学教育回报率的变化趋势，判断扩招政策对大学教育溢价的影响。

（四）数据与变量

本文有关高校扩招影响城镇劳动力收入水平的数据源自北京师范大学收入分配研究院提供的第五轮收入调查数据CHIP2013（城镇居民）。CHIP2013为收入分配研究院2014年组织的对城镇、农村居民以及外来务工人员的第五轮收入调查数据，采用了分层系统的抽样方法，随机选取了东、中、西部地区的15个省、126个城市、234个县，共计7175户城镇居民与17257个个体，最大限度地支撑了本研究所需的外部有效性。

表1报告了所涉变量的基本统计特征。被解释变量我们选取了城镇劳动力的年收入，同时作对数处理后代入方程（lnY）。从均值上看，城镇劳动力的收入水平随着时间的推移表现出增长的态势，对数收入由2007年的9.957增长到了2013年的10.285。此外，我们进一步通过表2刻画了城镇劳动力的受教育程度与收入分布的构成状态。我们选取了CHIP数据中接受正规学历教育的年限数定义教育年限（Educ），将教育年限在0-6年、7-9年、10-12年、13-16年以及16年以上等不同的取值区间，分别定义为小学、初中、高中、大学、研究生及以上教育层级。

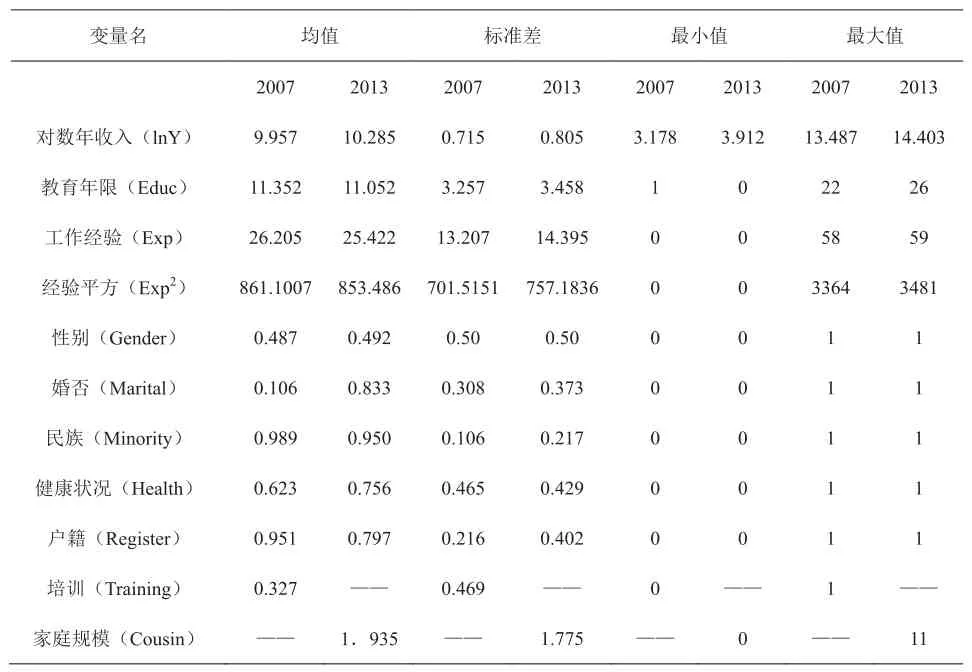
表1 数据描述

横向上看，城镇劳动力的收入水平与教育年限呈正相关，即受教育程度越高，收入对数的均值越高；纵向上看，同一教育层级内部，城镇劳动力2013年的收入水平要高于2007年。无论是横向对比还是纵向对比，受教育程度与年龄的关系均呈现出反向变动的趋势，即受教育程度越高则年龄越小，但需要指出的是，具有研究生及以上教育经历的劳动力，其年龄要大于大学教育层级，这是因为研究生教育延迟了城镇劳动力进入劳动力市场的时间。

表2 城镇劳动力的受教育程度与收入分层

有关经验（Exp）及其二次项（Exp2）的处理上，我们采用学界常用的处理办法，以劳动者接受调查的实际年龄减去接受学历教育的年限数，同时减去假定接受学历教育的起始年龄（6岁），得到工作经验，该处理办法较好地考虑了人力资本积累的持续性。图1是利用受教育程度、经验与收入对数制作的线性散点图，上半部分为2007年，下半部分为2013年。从线性关系上看（95%置信区间内），劳动力的人力资本积累与收入水平呈正相关性。

图1 2007-2013年城镇劳动力受教育程度、经验积累与收入水平的关系

此外，除了被解释变量与核心解释变量外，为了精确控制个体特征与家庭特征变量对教育回报率和大学教育溢价的影响，我们引入了性别（男性取1）、婚否（已婚取1）、民族（汉族取1）、健康程度（自我感觉健康取1）、户籍（非农取1）、是否接受培训（接受过取1）等变量作为控制变量组，对其做二元哑变量的设置，代入明瑟收入方程。

四、实证研究结果

（一）基准回归

在探讨高中阶段教育与大学教育对城镇劳动力的增收效应之前，我们首先基于方程（1），利用普通最小二乘法与工具变量法估计了城镇劳动力的整体教育回报率，同时采用两阶段样本选择模型纠正了样本选择偏差。表3报告了相关基准回归的结果，利用普通最小二乘法并消除标准误后，方程（1）中Educ的估计系数（）由2007年的0.071上升到了2013年的0.091，说明城镇劳动力的整体教育收益率由扩招前的7.1%上升到了扩招后的9.1%，实现了2个百分点的增长。

表3 基准回归结果

由于普通最小二乘法可能引致教育回报率的内生性偏估，因而我们采用工具变量法（IV）进一步估计方程（1）。鉴于本文旨在重点探讨高中阶段教育与大学教育的增收效应，我们并未采用父母的受教育程度或《义务教育改革法》作为工具变量。为了满足工具变量选取的既定原则——与城镇劳动力的受教育程度存在相关，但又与残差项不存在相关，我们以1999年作为扩招政策的起始年份，将《面向21世纪教育振兴行动计划》视为外生政策变量，并且假定城镇劳动力从6周岁起接受学历教育，历经九年制义务教育与三年制普通高中教育，于18周岁接受大学教育。如果说扩招政策的推行降低了大学准入的门槛，那么出生在1981年9月以后的劳动力，在理论上将有着更高的概率做出大学教育选择，而这也是本文工具变量设置的理论依据。

为了消除标准误的扰动，我们同样采用工具变量稳健标准差的回归形式估计整体教育回报率。从结果上看，将扩招政策视作外生变量的处理办法，通过了不可识别（Kleibergen-Papp）、冗余变量（LM test of redundancy of specified instrument）以及弱工具变量（Cragg-Donald）的一系列检验，具备统计学上的有效性，因而可以认为扩招政策作为大学参与的工具变量能够较好地消除内生性偏估。由于篇幅的关系，本文只报告了第二阶段的回归结果，变量Educ的估计系数由2007年的0.141下降到了2013年的0.091，也就是说，城镇劳动力的整体教育回报率由扩招前期的14.1%下降到了扩招后期的9.1%。这表明，假若我们忽视教育选择的异质性，那么遗漏变量的存在将低估扩招前期的教育回报率。

在赫克曼两阶段样本选择模型中，反米尔斯比率（λ）分别通过了1%与5%的显著性检验，说明城镇劳动力在进入劳动力市场时存在样本选择偏差。具体看来，2007年城镇劳动力的整体教育回报率由选择方程中的10.7%下降到了收入方程中的5%，说明样本选择高估了教育回报率；而2013年城镇劳动力的整体教育回报率则由选择方程中的9.9%上升到了收入方程中的10.7%，说明样本选择低估了2013年的教育回报率。对比两期截面数据的估计结果，我们发现在纠正了样本选择偏差后，城镇劳动力的整体教育回报率由2007年的5%上升到了2013年的10.7%，实现了5.7个百分点的增长。

最后，我们对接受高中阶段教育和大学教育的劳动力设置了二元哑变量，利用分教育层级回归估计大学教育收益率，将大学教育层级的估计值与高中阶段相减，同时除以假定相同的大学教育年限（4年），得到2007年与2013年大学教育的年收益率分别为8.7%和9.65%，而相应的高中阶段年收益率分别为6.4%和7.8%。2007年和2013年大学教育年收益率相对于高中阶段要分别高出2.3和1.85个百分点，这表明即使高校扩招政策的推行向劳动力市场供给了过量的技能型劳动力，但大学教育相对于高中教育而言仍然是一项有效的人力资本投资。工作经验方面，一次项的估计值为正，二次项的系数为负，并且在各方程中均具备统计学上的显著意义，说明“干中学”、人职匹配等经验的积累以倒U型的方式影响收入增长，即随着人力资本的消耗以及工龄对退休年龄的逼近，越过“拐点”后的经验延长，对收入增长的促进作用将更为发散，而这一点也符合加里·贝克尔提供的年龄-收入曲线。个体与家庭特征构成的控制变量方面，男性、身体更为健康的个体、接受过职业培训以及家庭规模较小的个体，其收入水平相对于参照组而言要更高。

（二）大学教育的处理效应估计

1.大学参与的概率估计

本小节将利用倾向得分匹配的原理，根据城镇劳动力是否接受大学教育，将样本划分为接受大学教育的处理组和高中阶段教育后直接进入劳动力市场的参照组，构建反事实选择的解释框架，着重探讨高校扩招政策对大学教育溢价的影响。我们对表4报告的城镇劳动力大学参与的logit模型估计结果做出简单报告：工作经验对大学参与的概率形成负向影响，说明高中毕业后直接做出大学教育选择的概率要高于先进入劳动力市场再做出大学教育决策的概率，这一估计值与刘泽云（2011）[23]对高等教育质量的估计结果较为一致。男性、非农户籍的个体有着更高的概率选择接受大学教育。

表4 城镇劳动力大学参与的概率水平估计

2.平衡性检验

我们将参照组中的个体收入作为处理组的反事实选择状态，利用倾向得分匹配估计大学教育的处理效应之前，需要对明瑟方程中的协变量进行平衡性检验，旨在考察匹配后的数据是否能够实现有效的平衡。根据表5给出的平衡性检验结果，我们发现在完成数据匹配后，处理组与参照组下协变量的标准化偏差（Bias）显著缩小，并且双t检验的p value在匹配后实现上升。这表明处理组与参照组中变量的特征差异得到有效控制，即消除了城镇劳动力在做出教育选择前的个体、家庭等方面的背景差异。因此，我们有理由认为，城镇劳动力在结束高中阶段教育后，是否做出大学教育选择并接受大学教育，仅仅由大学教育所带来的预期收益以及对自身比较优势的判断所决定，因而协变量在两组下具有一致的分布特征。此外，协变量的倾向得分匹配图也显示出数据匹配后具有良好的平衡性（图2）。

3.大学教育的处理效应

在数据匹配平衡的基础上，考虑到多种识别策略有利于检验大学教育溢价的估计是否稳健，我们采取四种识别策略估计扩招前与扩招后的大学教育溢价水平，即近邻匹配（Neighbor K）、半径或被称作卡尺匹配（Radius）、核匹配（Kernel）以及马氏匹配（Mahal）。其中，近邻匹配选取K=4；半径匹配选取卡尺在不太远的“近邻”范围内，即Cal=0.01；核匹配选取默认的核函数与相应的带宽；马氏匹配则选用Adabie&Imbens（2006）提供的异方差标准误的估计形式。表6报告了四种估计策略下的大学教育溢价水平。

表5 协变量的平衡性检验

图2 数据匹配平衡图

根据平均处理效应的估计值可知，大学教育溢价在四种识别策略下的估计结果较为一致与稳健。2007年处理组中，城镇劳动力的大学教育溢价落入[0.380，0.390]的取值区间内，并据此计算出大学教育的年收益率则落入[9.5%，9.75%]的取值区间内，而该估计值要高于分教育层级基准回归中的8.7%；同时，2013年处理组中，城镇劳动力的大学教育溢价水平则落入[0.457，0.477]的取值区间内，并据此计算出大学教育年收益率则落入[11.425%，11.925%]的取值区间内，而这一估计值同样高于分教育层级回归中的9.65%。因此，将基准回归估计结果与倾向得分匹配法的估计结果进行对比后，我们发现反事实选择偏差将造成大学教育溢价的低估。此外，将大学教育的处理效应进行对比，我们发现2013年的大学教育年收益率高于2007年。因此，我们有理由相信，城镇劳动力在扩招政策开启后，做出大学教育选择并实际接受大学教育，并未显著降低个体大学教育溢价。

表6 大学教育溢价的处理效应估计

五、结论与探讨

（一）研究结论

本文采用北京师范大学收入分配研究院提供的CHIP2013数据，综合采用微观计量领域内的实证研究方法，构建大学教育与高中阶段教育的反事实选择框架，揭示了高校扩招政策、城镇劳动力大学教育溢价以及工资收入差距间的因果关系，研究发现：

第一，基准回归方面，利用OLS发现城镇劳动力的整体教育回报率不断上升，由2007年的7.1%增长到了2013年的9.1%；分教育层级的回归结果表明，大学教育年收益率由2007年的8.7%增长到了2013年的9.65%，并且高于高中阶段的估计值；但选取高校扩招政策作为工具变量，利用工具变量法的估计却发现，整体教育回报率由2007年的14.1%下降到了2013年的9.1%，说明遗漏变量的存在导致了教育收益率的向上或向下偏估；利用赫克曼两阶段样本选择模型，纠正了劳动力市场的样本选择偏差后，整体教育回报率由2007年的5%上升到了2013年的10.7%。

第二，利用倾向得分匹配法实现数据平衡后，通过平均处理效应估算出大学教育的年收益率由2007年的 9.5%～9.75%上升到了 2013年的11.425%～11.925%，验证了本文的研究假设，即高校扩招政策的推行并未降低城镇劳动力的大学教育溢价，大学教育相对于高中阶段教育而言，仍然是一项高效的教育人力资本投资。同时，倾向得分匹配法对大学教育年收益率的估计值要高于分教育层级回归，说明反事实选择偏差造成了大学教育收益率的低估。

（二）延展讨论

政策含义方面，根据表2可知，城镇劳动力在大学教育层级的占比由2007年的26.19%略微上升到了26.53%，保持小幅增长的态势，但研究生教育层级的劳动力占比却由2007年的3.42%小幅下降到了2013年的1.85%。因此，我们认为，在保证本科规模稳定的同时，可将大学扩招的层级适度上移，在后大众化发展时期，适度放宽博士生“申请-考核”制的门槛，通过硕士与博士两级研究生教育层级的稳步扩张，尤其是专业博士招生规模的稳步扩大，逐步提高研究生劳动力在经济活动人口中的比重，优化当前人力资本的分布结构。需要注意的是，研究生教育位于高等教育金字塔的顶端，是一国拔尖创新人才的集中反映，因此，对于研究生教育规模扩张切勿极端冒进，而应走内涵式发展道路，坚持早发内生型的战略路径选择。同时，研究生教育规模扩张应注重与劳动力市场、产业结构的变动紧密结合，并契合“中国制造2025”的大政方针，有针对性地向专业技术型或服务型等行业输送研究生人力资本，最终以研究生教育为发展杠杆，提高全体劳动力的受教育程度与收入水平，进一步缩减收入差距，实现教育扶贫的目标。