非绝热分子动力学模拟A位阳离子对钙钛矿热载流子弛豫的影响

贺进禄,龙 闰,方维海

(北京师范大学化学学院,理论与计算光化学教育部重点实验室,北京 100875)

影响热载流子能量弛豫的因素有外界的实验条件[14]、材料本体的性质[3,15]以及组分调控[16,17]等. Yang等[14]通过瞬态吸收光谱研究了激发光的强度对于热载流子能量弛豫的影响,增加激发光的强度能够延长热载流子能量弛豫时间. Zhu等[3]提出了大极化子的形成能够延缓热载流子能量弛豫,提高钙钛矿太阳能电池的效率. Fu等[15]认为热声子瓶颈和俄歇热效应是延缓热载流子能量弛豫的2个关键因素,并提出中等载流子浓度时热声子瓶颈效应起主导作用,而在载流子浓度高时俄歇热效应起主导作用. 另有实验通过调控铅卤钙钛矿的组分来延长热载流子能量弛豫时间[16～18]. 如Chung等[16]发现铅卤钙钛矿中的热载流子的寿命依赖于其卤素的组分,Fang等[18]通过将铅卤钙钛矿中的铅替换为锡之后,发现热载流子寿命提高了3～4个数量级. 理论计算表明,A位阳离子对于钙钛矿的热载流子能量弛豫范围内的价带和导带的态密度贡献微乎其微[19～21],但是大量实验结果表明A位阳离子对钙钛矿热载流子弛豫动力学有显著影响[3,17,22]. 如Chen等[17]运用飞秒瞬态吸收光谱方法研究了APbBr3(A=Cs+,MA+,FA+) 弛豫动力学,结果显示,热载流子能量弛豫时间的变化顺序为CsPbBr3>MAPbBr3>FAPbBr3,这一现象的物理机制有待进一步的理论模拟来揭示.

Fig.1 Schematic diagram of hot carrier energy relaxation dynamicsin the perovskite system

图1给出了热载流子能量弛豫的动力学过程. 半导体材料被大于其带隙的高能量的光激发后,电子被激发到导带,空穴留在价带,随后电子和空穴发生分离. 具有高于导带底和价带顶的电子和空穴被称为热载流子. 被激发的电子从能量高于导带底ΔEe的位置弛豫到导带底,发生热电子弛豫. 而被激发的空穴从能量高于价带顶ΔEh的位置弛豫到价带顶,发生热空穴弛豫. 这两个过程均伴随着电子能量损失到晶格振动,降低了太阳能电池的光电转换效率.

为了深入理解这一现象的本质,本文采用基于含时密度泛函理论的非绝热分子动力学方法研究了铅卤钙钛矿CsPbBr3,MAPbBr3和FAPbBr3体系A位阳离子对热载流子能量弛豫动力学的影响. 研究结果表明,A位阳离子对热载流子能量弛豫产生了显著的影响. 同时发现阳离子通过静电或氢键作用影响Pb—Br骨架的振动,进而改变非绝热耦合的强弱,研究A位阳离子影响热载流子弛豫快慢的物理机制,可为进一步提高钙钛矿太阳能电池的性能提供新的思路.

1 计算方法

对非绝热分子动力学模拟采用含时密度泛函理论[23]框架下的最少面间跳跃方法(FSSH)[24～26]进行计算,其中对运动快、质量轻的电子采用量子力学处理,而对运动慢、质量重的原子核运用经典力学处理.

1.1 含时密度泛函理论

含时密度泛函理论[23]将系统的电子性质与电子密度联系起来,用已占据的单电子含时Kohn-Sham(KS)轨道[Φp(r,t)]的密度和来表示:

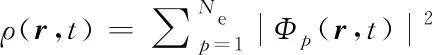
(1)

式中,Ne为电子数,电子密度的演化由含时变分原理求得的KS密度泛函的期望值决定. 在平均场或单粒子近似下,一组KS轨道的演化方程[27,28]为

(2)

(3)

将式(3)带入式(2),获得描述展开系数演化的方程[25]:

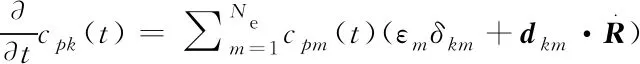
(4)

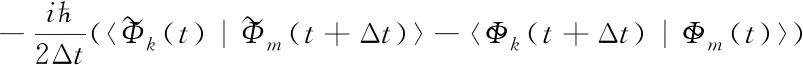
(5)

1.2 最少面间跳跃法

在FSSH方法中,核运动采用经典力学处理,但包含了电子在不同绝热态之间的跃迁[27,29,33]. 借助于含时密度泛函电子结构计算,利用式(4)可以得到FSSH方法需要的展开系数的演化方程,从而可以计算从电子态k跃迁到电子态m的几率:

(6)

通过计算dPkm来判断电子态k跃迁到电子态m可能性,当dPkm的计算值为负数时,跃迁概率设置为零. 在判断电子态之间的跃迁时,需要产生一个随机数ξ∈[0,1]:

(7)

如果概率满足式(7),电子态k则跃迁到电子态m. 通过调整非绝热耦合矢量方向上的核运动速度,可以保证跃迁后的能量守恒[31]. 如果非绝热跃迁到一个更高能量的电子态时,沿非绝热耦合矢量方向的核动能不足以补偿电子能量的增加,则跃迁过程被禁止[32～34]. 这一步骤给出了能量向上和向下之间转变的细致平衡,近似满足玻尔兹曼统计和量子经典热力学平衡[30]. 目前简化的FSSH方法假设电子与振动自由度之间的能量交换在所有的振动模式中都被迅速地重新分配. 在此假设下,能量在振动模式中的分布始终是玻尔兹曼分布,速度的重新缩放加上跳跃禁阻可以用能量向上跃迁的概率乘以玻尔兹曼系数来代替. 这种简化大大提高了该方法的计算效率[35]. 该方法被广泛应用于钙钛矿[36]、碳材料[37]、二硫化钼[38]及其它材料[39]的激发态动力学研究中.

1.3 计算过程

通过VASP[40](Viennaabinitiosimulation package)软件包对几何优化、电子结构、绝热分子动力学和非绝热耦合进行计算. 其中交换相关能和离子实与价电子之间的相互作用分别采用PBE(Perdew-Burke-Ernzerhof)泛函[41]和PAW(projector-augmented wave)方法[42]描述. 平面波截断能设置为400 eV,采用4×4×4 Monkhorst-Pack网格点[46]进行几何结构优化,当离子弛豫受力小于0.1 eV/nm时,达到收敛标准,优化停止. 为了获得准确的电子结构,态密度计算采用更稠密的8×8×4 Monkhorst-Pack点网格[43]. 运用Grimme DFT-D3方法处理范德华相互作用[44]. 为了模拟A位阳离子对铅溴钙钛矿中热载流子能量弛豫动力学的影响,以立方晶相的单胞构建了2×2×2的3种体系的超晶胞. 其中,CsPbBr3体系含有40个原子,MAPbBr3和FAPbBr3体系均包含96个原子. 采用优化的平衡结构,通过速度重复缩放将体系加热至室温,然后在微正则系综中以1 fs的时间步长进行6 ps绝热分子动力学模拟. 为了模拟热载流子能量弛豫动力学,随机抽样1000个几何结构作为非绝热分子动力学模拟的初始条件.

2 结果与讨论

2.1 几何结构

图2给出了0 K优化的和300 K分子动力学轨迹选取的有代表性的几何结构. CsPbBr3,MAPbBr3和FAPbBr3体系优化的晶格常数分别为0.5900,0.5920和0.5990 nm,与实验值0.5870[45],0.5919[46]和0.5994 nm[47]吻合. 在0 K下,CsPbBr3,MAPbBr3和FAPbBr3计算的平均Pb—Br键键长分别为0.2950,0.2974和0.3002 nm,与实验值0.2960[51],0.2970[48]和0.3000 nm[49]一致; 当体系温度为300 K时,对应的平均键长增加到0.3087,0.3088和0.3098 nm,依次增加了4.64%,3.83%和3.20%. 从键长的变化值可见,3种钙钛矿体系Pb—Br键键长变化都较小,表明3种体系的无机骨架具有很高的稳定性. 键长变化幅度可以由A位阳离子与无机Pb—Br骨架的静电[50]或氢键[51,52]作用来解释. Cs+与无机Pb—Br骨架之间只存在较弱的静电作用,而MA+和FA+与无机Pb—Br骨架之间除了较弱的静电作用还存在较强的氢键作用. 虽然MA+具有更大的偶极矩,但其与无机骨架之间的静电作用强于FA+,但是FA+的离子半径大于MA+,H与Pb/Br的距离更近,导致其与无机骨架的氢键作用强于MA+[51]. 考虑到氢键作用远强于静电作用,3种钙钛矿中A位阳离子与无机Pb—Br骨架之间的相互作用顺序为FAPbBr3>MAPbBr3>CsPbBr3,较强的相互作用抑制了Pb—Br键键长变化和无机原子的运动. 理论研究结果表明,铅卤钙钛矿的非绝热耦合主要由铅和卤素贡献,A位置阳离子对其贡献非常小[6]. 本文使用的3种体系的超晶胞含有相同的Pb和Br原子数,分别为8和24,排除了3种钙钛矿体系Pb/Br原子本身对非绝热耦合差异的影响. 因此,非绝热耦合强度的差异只能来源于A位阳离子与无机Pb—Br骨架之间的相互作用. 这种相互作用越强,非绝热耦合则越强. 因此,3种钙钛矿中非绝热耦合强度的变化趋势为FAPbBr3>MAPbBr3>CsPbBr3.

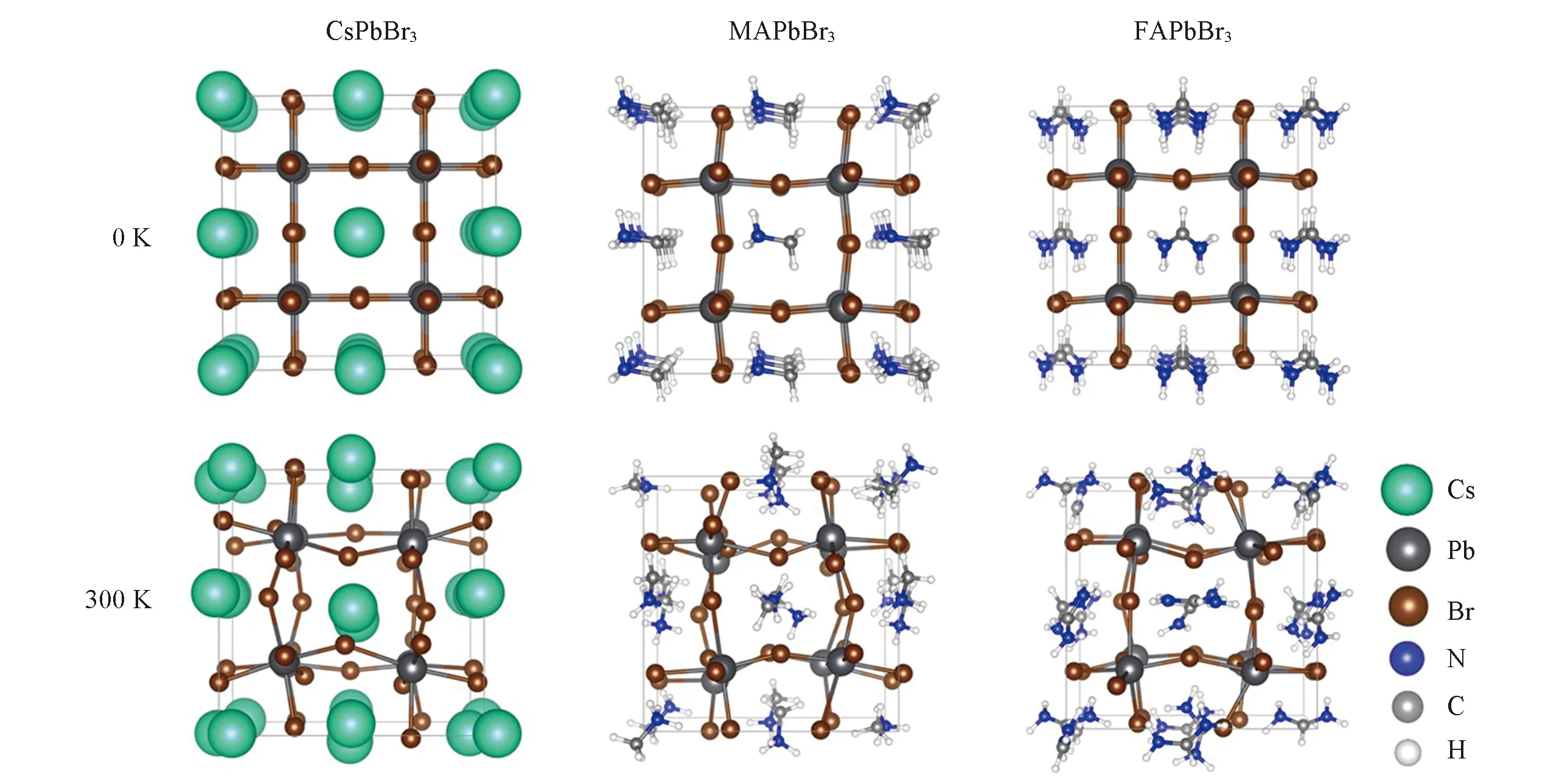
Fig.2 Simulation cell showing the optimized geometry and a representative snapshot of molecular dynamics at 300 K of CsPbBr3,MAPbBr3 and FAPbBr3

Fig.3 Projected density of states(PDOS) of CsPbBr3(A),MAPbBr3(B) and FAPbBr3(C) systems

2.2 电子结构

图3给出了采用优化的几何结构计算的CsPbBr3,MAPbBr3和FAPbBr3体系的投影态密度(PDOS),带隙值分别为1.60,1.94和1.91 eV,与文献[51,53]采用PBE泛函的计算结果相吻合. 根据实验结果[17],热载流子过剩的能量在 0.6 eV以内. 图3的投影态密度区分了Pb,Br和A位阳离子对总态密度的贡献. 一方面,在给定的能量区间内,态密度主要由Pb和Br原子的轨道贡献,它们是非绝热耦合的主要来源,对热载流子弛豫过程起主导作用. 尤其是导带主要由Pb贡献,价带主要由Br贡献. 因此,可以通过改变钙钛矿中金属元素和卤素组分,调控其热电子和热空穴能量弛豫动力学. 另一方面,虽然A位阳离子对选定能量区间的态密度贡献很小,但是通过静电/氢键作用影响其与Pb—Br骨架的相互作用[50～52],从而间接影响非绝热耦合强度和热载流子弛豫过程.

2.3 热载流子能量弛豫动力学

由于实验中的热载流子能量ΔE约为0.4和0.6 eV[17],所以选取了分别高于导带底和价带顶0.4和0.6 eV 的两个电子态为初始态模拟热载流子弛豫过程. 图4为非绝热动力学模拟得到的CsPbBr3,MAPbBr3和FAPbBr3体系中热载流子能量弛豫动力学. 图4(A)和(C)分别为ΔEe=0.4和0.6 eV的热电子能量弛豫动力学. 图4(B)和(D)分别为ΔEh=0.4和0.6 eV的热空穴能量弛豫动力学. 图4标记的热载流子能量弛豫时间采用指数函数拟合得到,E(t)=aexp(-t/τ)+b. 由图4可见,热电子和热空穴的能量弛豫动力学依赖于A位阳离子的种类: (1) 计算的热载流子时间尺度在几百fs到几个ps,与实验测得的时间尺度较为接近[17]; (2) 热电子和热空穴能量弛豫时间的顺序为CsPbBr3>MAPbBr3>FAPbBr3; (3) 能量越高,热载流子弛豫越快.

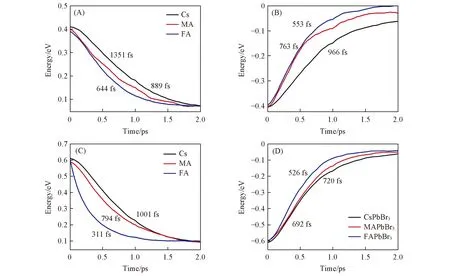
Fig.4 Time evolution of the energy decay dynamics of hot electrons with 0.4 eV(A)and 0.6 eV(C) excess energies,and hot holes with 0.4 eV(B) and 0.6 eV(D) excess energies

为了探究CsPbBr3,MAPbBr3和FAPbBr33种钙钛矿体系中热载流子能量弛豫快慢的微观本质,在4 ps分子动力学模拟的基础上,计算了导带和价带中参与热载流子能量弛豫过程相邻电子态及非相邻电子态之间的非绝热耦合强度,并推得其绝对值的平均值,如图5所示. 二维图的对角线代表相邻电子态间的非绝热耦合,非对角线代表非相邻电子态间的非绝热耦合. 3种体系沿对角线的耦合都很强,表明相邻态之间最可能发生非辐射跃迁,其主导了热载流子弛豫动力学快慢. 远离对角线耦合较弱,这是因为非绝热耦合强度与能级差成反比[54],其对热载流子弛豫起次要作用. 因此,图5进一步表明相邻电子态之间的非绝热耦合强度依次为FAPbBr3>MAPbBr3>CsPbBr3. 相应地,热载流子弛豫时间满足相反的趋势CsPbBr3>MAPbBr3>FAPbBr3. 同理,能量越高,包含的近邻电子态之间的非绝热耦合强度越强,弛豫越快.

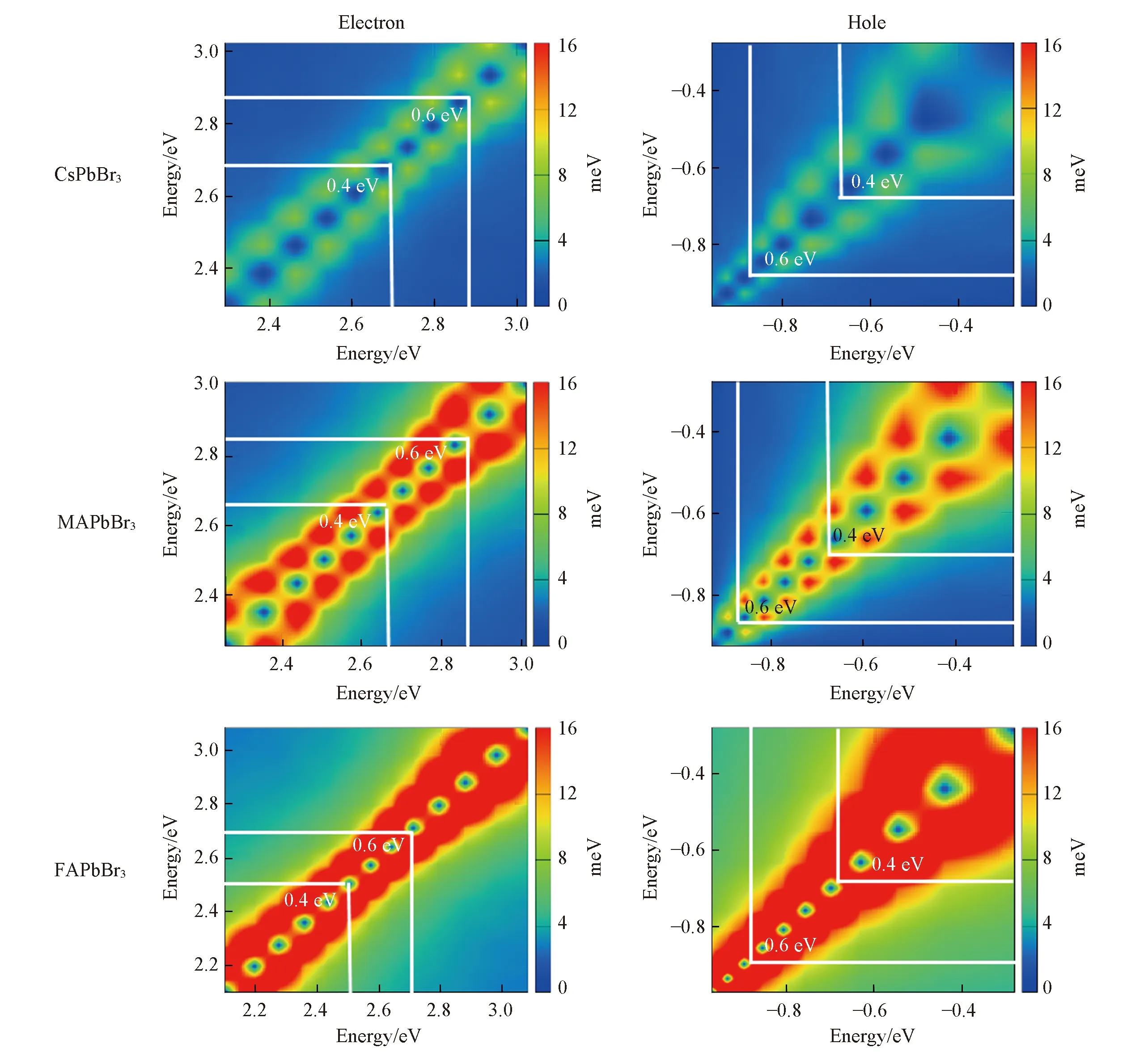
Fig.5 Average magnitude of the nonadiabatic couplings for hot electrons and holes relaxation within conduction band and valence band of the CsPbBr3,MAPbBr3 and FAPbBr3

综上所述， 采用含时密度泛函理论结合非绝热分子动力学研究了A位阳离子对CsPbBr3,MAPbBr3和FAPbBr33种钙钛矿热载流子能量弛豫过程的影响. 计算结果表明,热载流子能量弛豫均发生在几百fs至几个ps的时间尺度内,与实验测得的时间尺度较为接近. 热载流子能量弛豫过程发生快慢依赖于A位阳离子,这是因为A位阳离子通过静电与氢键与无机Pb—Br骨架相互作用,协同影响了非绝热耦合强度. 综合静电和氢键作用(FA+>MA+>Cs+)使非绝耦合强度大小具有相同的变化趋势. 因此,热载流子弛豫FAPbBr3体系最快,MAPbBr3次之,CsPbBr3最慢,并且过剩能量越大,非绝热耦合强度越大,热载流子能量弛豫越快. 因此通过改变A位阳离子,可延缓钙钛矿材料中载流子能量损失,进一步优化钙钛矿太阳能电池的性能.