基于公交车辆定位数据的公交运送速度计算模型
2020-03-12翁剑成张乐典王晶晶钱慧敏
祁 昊,翁剑成,张乐典,王晶晶,钱慧敏
(1.北京工业大学北京市城市交通运行保障工程技术研究中心,北京 100124;2.交通运输部科学研究院,北京 100029;3.青岛市城市规划设计研究院,青岛 266071;4.北京市交通运行监测调度中心,北京 100073)
0 引言
公共交通在城市居民出行中承担着主要的乘客运输和通勤出行任务,其运送速度直接影响居民出行的效率.传统的公交速度采集方法多以跟车调查、断面调查等人工采集数据或固定式交通信息采集设备数据为基础[1-3],存在覆盖范围有限、人力和物力资源投入过高等问题.随着公交车载GPS系统的推广应用,为实时获取公交运送速度提供了新的数据基础.如何从GPS数据中准确地提取公交运送速度,成为公交数据处理领域的关键问题.
国内外学者在公交运送速度计算及应用方面进行了大量研究,主要集中在公交行程时间预测、运行速度估计以及道路信息获取等方面.在公交行程时间预测方面,部分学者探究了行程时间预测的影响因素[4-5],并对行程时间进行预测.Padmanaban等[6]建立了一套基于实时GPS数据的公交到站预报系统,将复杂交通流条件下的公交延误时间纳入了计算.王殿海等[7]结合GPS数据和地图匹配算法计算路段的行程时间,验证了行程时间计算模型的准确性.在公交车辆速度估计方面,Cristian E.Cortés等[8]提出了通过建立时间和空间二维网格来计算公交车辆速度的方法.肖倩[9]利用公交GPS回传的瞬时速度值,建立地图的匹配规则等处理流程对路段的公交平均速度进行估计.宗高勤等[10]利用公交车辆历史GPS数据,结合公交线路地理位置信息,分析了公交线路的速度特性.此外也有学者以公交车作为浮动车来获取道路路况信息[11-12].
现有研究更多关注于公交到站预报等局部应用,对公交全过程的运行状态描述和刻画并不准确,难以满足对公交运行状况连续的准确监测.因此,本研究从微观层面着手,基于公交车辆实时GPS定位数据,实现对每一辆公交车辆运行状态连续的准确监测,从而获取公交站点区间、公交线路以及公交线网的实时运行状态,更加深入地了解公交系统运行规律,为加强地面公交日常监管、辅助运营管理决策、提升公交信息服务水平、改善乘客公交出行满意度提供准确的数据和模型支撑.
1 基础数据准备
公交车辆实时回传的GPS数据以及基于GIS地图的线路数据是本研究构建公交运送速度计算模型的2类基础数据.
1.1 公交GPS数据
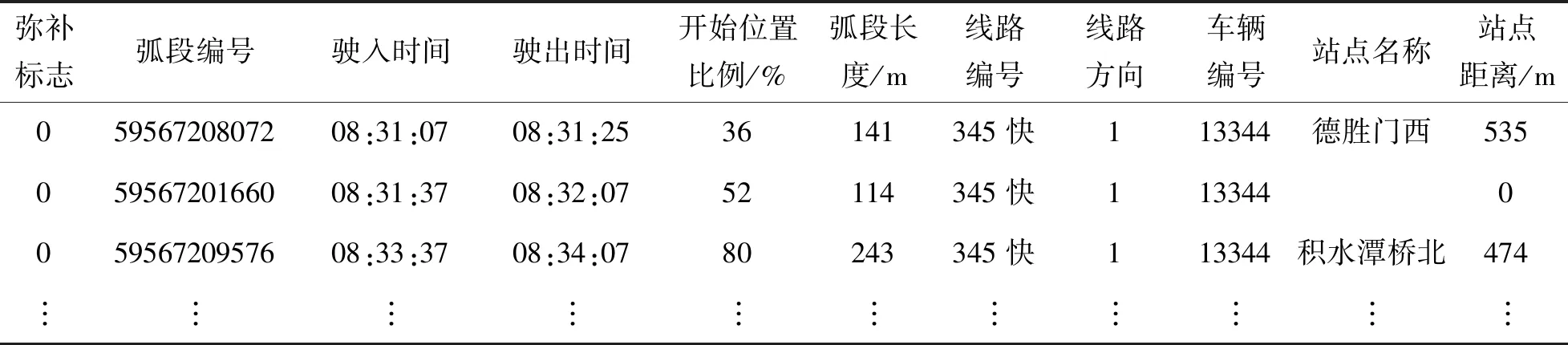
本文所使用的公交车辆GPS定位数据取自北京公共交通集团,数据主要字段和示例如表1所示.
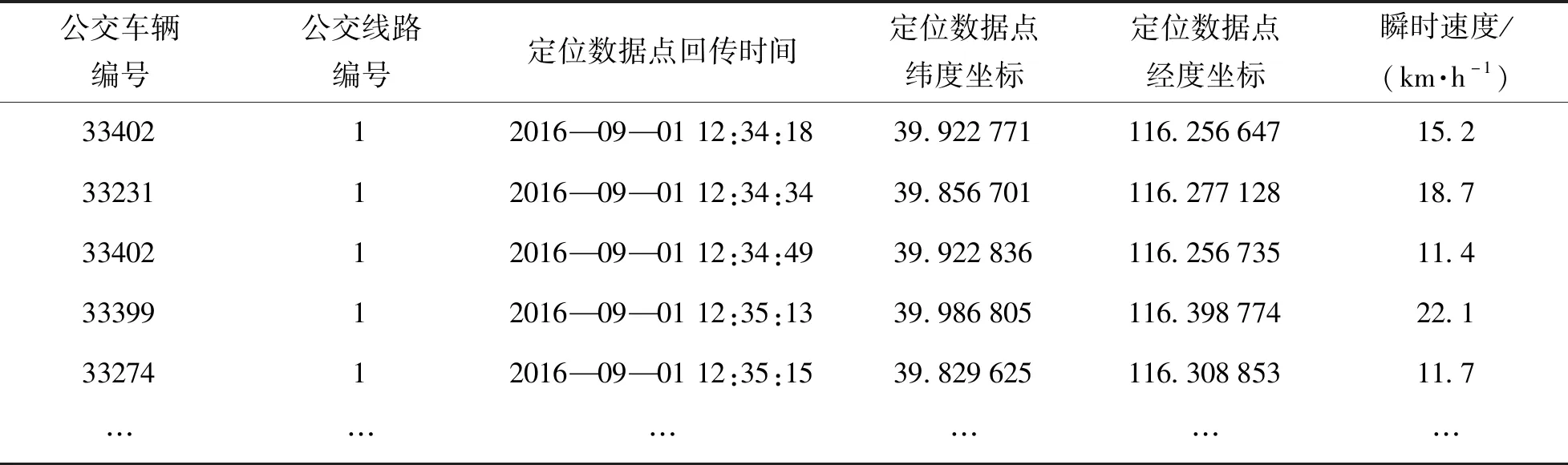
表1 公交GPS数据
原始的GPS数据需要经过坐标转换与偏移、坐标合理性判断等预处理过程,才能成为公交运送速度计算的有效数据.研究通过采用统一坐标系的方式,将公交车辆GPS定位数据与地图进行合理匹配.因此,当原始数据所属的坐标系与研究所采用地图的坐标系不一致时,需要将原始数据的经纬度坐标向研究所采用地图的坐标系进行转换.最后,将处理后的GPS坐标点逐一匹配到地图上判断坐标合理性,即经纬度处于研究区域内,并判断数据字段的完整性,筛选出满足条件的数据,作为公交运送速度计算的有效数据.
1.2 公交线路数据
公交线路数据主要包含2类信息:一是线路经过的所有的弧段信息;二是线路上各公交站点在相应弧段中的位置信息.获取公交线路数据的步骤如下所示.
1.2.1 站点聚合,确定站点唯一坐标
由于各条公交线路的站点位置信息相互独立,不同线路同一个站点的坐标数值存在差异,因此研究假定相同站名的公交站点具有相同的经纬度坐标.通过对公交站点位置进行聚合处理,把站名相同的公交站点设定为相同的经纬度坐标,并且每个聚合公交站点在单一的上下行方向中,有且仅有唯一的经纬度坐标,如图1所示.
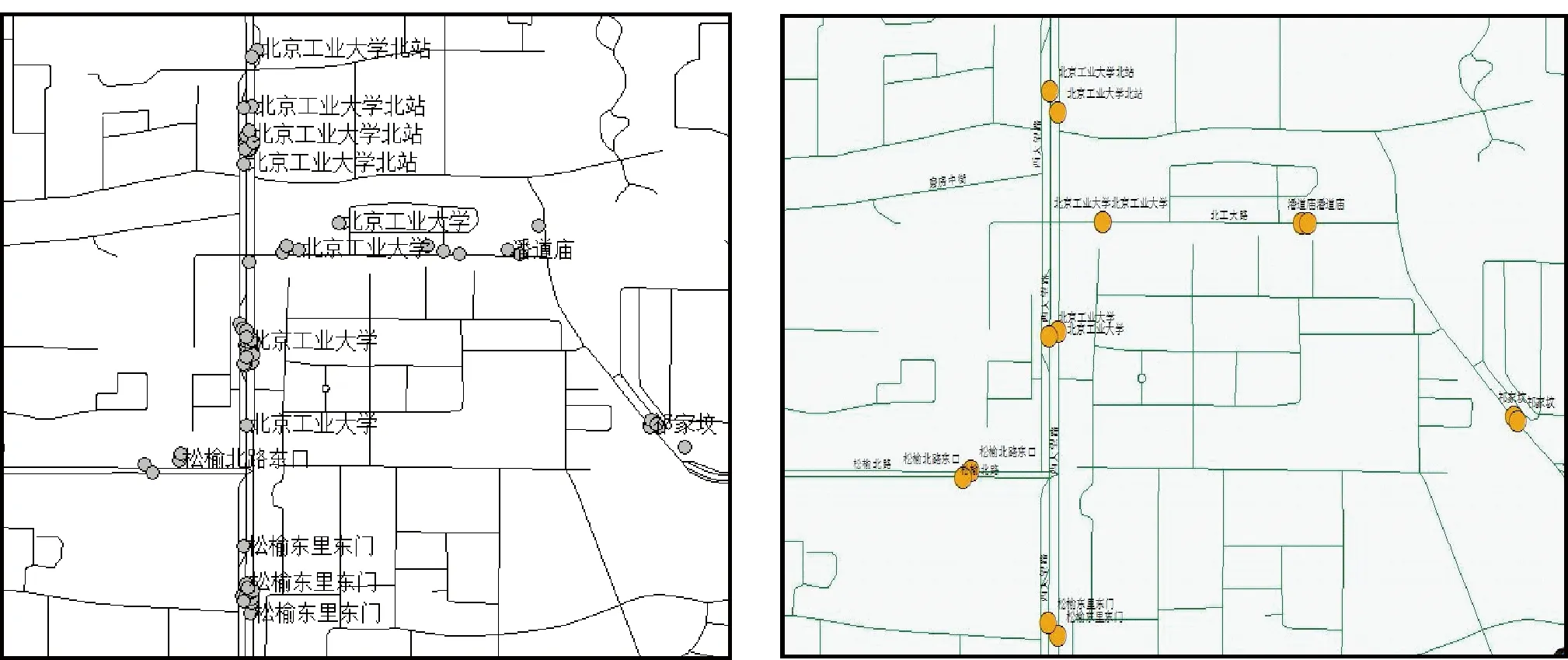
图1 聚合公交站点
1.2.2 按照线路路径,提取弧段信息
基于A*star算法寻找公交车辆的运营路线,计算最短路生成公交线路的初始路径.
由于通过A*star算法所获取的初始公交车辆行驶路径存在道路弧段间断或与实际公交运营路线不匹配等情况,需要结合人工核对的方式对每条公交线路进行调整.通过与线路实际运行轨迹进行对照,确保模型运算的准确性.
1.2.3 确定公交站点在弧段中的位置
为了准确计算公交车辆的到站时间,需要对公交站点位于道路弧段的比例位置进行确定式(1):
(1)
式中,Is为公交站点在道路弧段上的位置比例(%);ds为公交站点至道路弧段起点的距离(m);dl为公交站点对应道路弧段的长度(m).
1.2.4 完成公交线路数据表
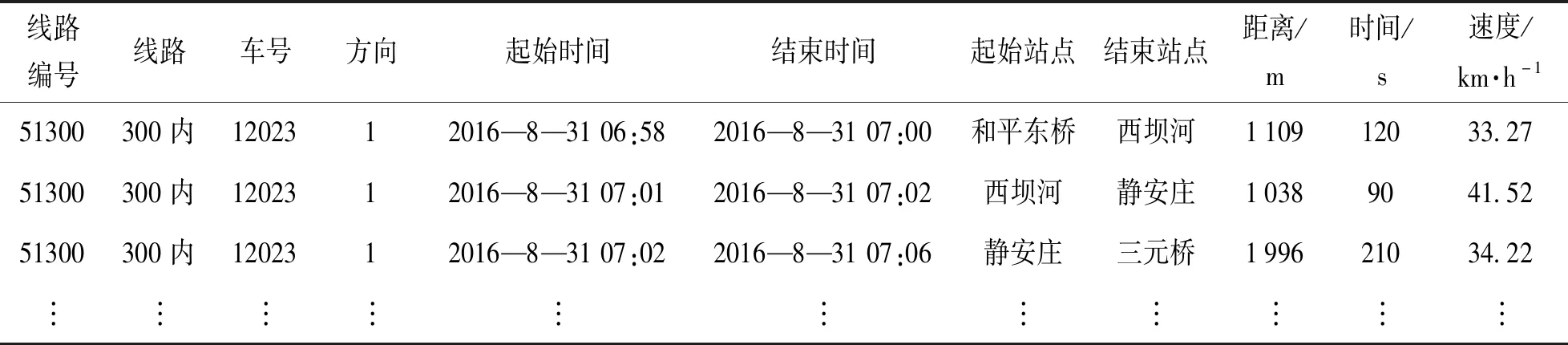
最后,通过对公交线路及站点的位置信息校核匹配,生成公交线路数据表,主要记录线路双方向的弧段信息、聚合后的站点经纬度以及站点间距等信息,如表2所示:

表2 公交线路数据
2 公交运送速度计算模型
2.1 公交运送速度计算流程
描述公交运送速度的最小单元是公交站点区间.在公交车辆GPS定位数据预处理和公交线站数据准备的基础上,进行地图匹配和运送速度计算.首先将GPS数据点向指定的线路弧段投影,完成GPS点位置匹配和投影点弧段分位计算;然后判断匹配弧段的连续性,进行弧段弥补;根据公交车辆GPS定位点与公交站点位置的匹配,识别公交到站时间;通过识别所匹配的站点次序,确定车辆行驶方向,提取车辆行驶轨迹数据;最后利用相邻站点间公交运行的时间间隔和站点间距,计算站点区间公交运送速度.模型的计算结果需要根据不同等级道路的区间运送速度阈值进行校核与修正,并定期对线路站点基础信息进行校验,避免线路调整对速度计算模型精度的影响,从而完成最终的结果输出,流程如图2所示:

图2 公交运送速度计算流程图
2.1.1 位置匹配与弧段分位计算
首先假定车辆行驶方向为1(方向1为上行、内环方向;方向2为下行、外环方向),对GPS点进行全弧段序列的匹配,逐一将GPS点匹配到所在的弧段编号和弧段位置.
1)将GPS点向指定线路的弧段上投影,考虑到GPS误差的情况,当最小垂直距离>100 m时,则认为该点匹配不成功,放弃该点数据.
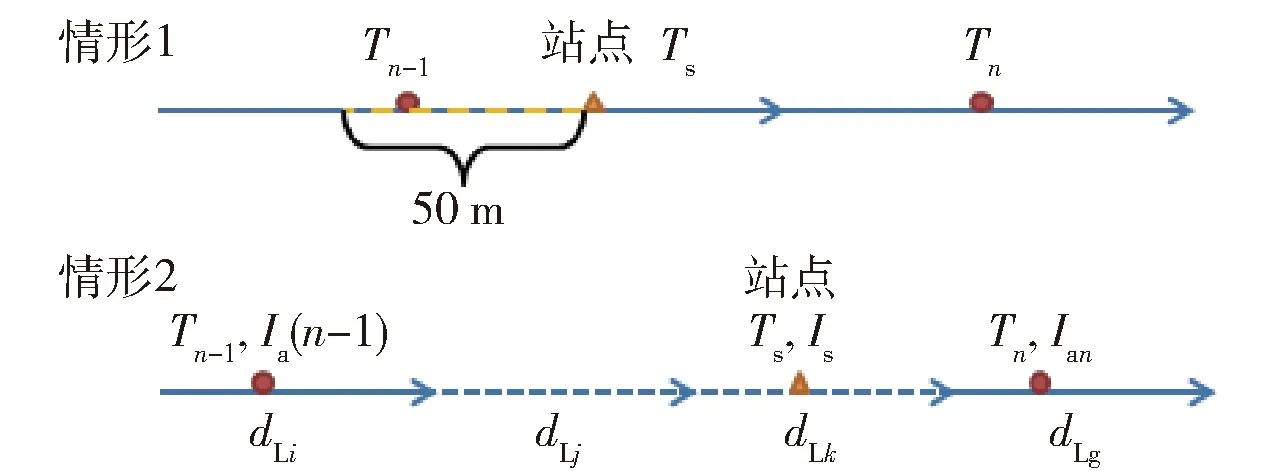
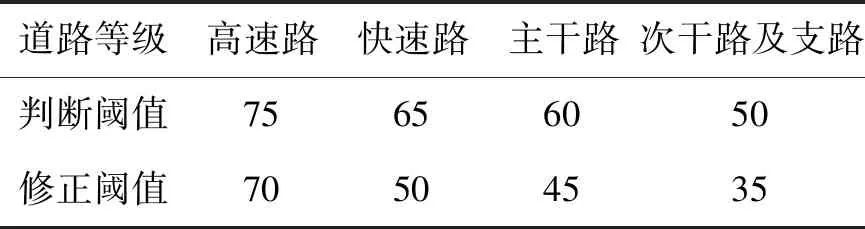
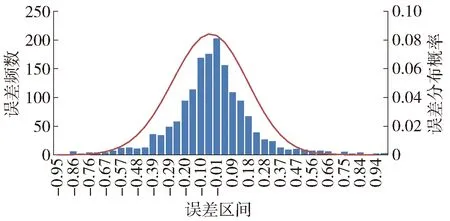
情形1:当GPS点可向多条指定弧段投影时,垂直距离最小者为该点所在弧段.如图3所示,当d1 图3 GPS弧段位置匹配 情形2:对于双向异路的线路,如果在假设的行驶方向上连续匹配不成功的GPS点数量>4时(由于全部线路的最大GPS点时间间隔为15 s,当未在规定的线路上行驶超过1 min时,认为匹配失败),调换线路行驶方向,重新匹配所有GPS点序列,如图4所示. 2)计算GPS投影点弧段位置比例 为了满足计算需要,判断GPS定位数据投影点 图4 双向异路GPS匹配示意图 在弧段上的位置比例: (2) 式中,Ia为GPS投影点弧段位置比例(%);da为弧段起点至GPS投影点的矢量距离(m);dL为弧段长度(m). 通常Ia处于[0,1]区间内.但在以下2种情况下,允许Ia为负值或Ia>1,如图5所示. 情形1:起点站附近GPS点匹配.为保证线路第1个弧段上的站点在连续的2个GPS投影点之间,允许GPS点向第1个弧段的延长线投影,则da为负. 情形2:终点站附近GPS点匹配.为保证线路最后1个弧段上的站点在连续的2个GPS投影点之间,允许GPS点向最后1个弧段的延长线投影,则da的长度将>dL,Ia的值>1. 2.1.2 弧段连续性判别与弥补 由于公交车辆GPS定位数据的传输受周围建筑物影响,会出现连续GPS点间回传间隔时间较长的现象,导致弧段匹配不连续.本研究根据弧否连续.若不连续,且不满足以下2辆行驶轨迹记录中增添缺失的弧段信息. 1)如果连续2个GPS点时间间隔超过10 min,则废弃数据重新计算. 2)计算2个GPS定位数据点间的直线行驶速度,如果≥75 km/h(高速路上公交车辆行驶的最大速度阈值),则认为该点为异常数据,废弃该点数据. 2.1.3 公交到站信息匹配 判断2个GPS定位数据点间是否存在站点.根据公交站点与GPS定位数据点间的空间关系,识别公交到站时间.根据不同的公交站点与GPS点间的空间位置关系,到站时间匹配的方法也有所不同,如图6所示. 图6 到站信息匹配 情形1:站点位于GPS回传点附近. 对于停靠公交线路较多的公交站点,在早晚高峰期间经常出现公交车辆在公交站台前集聚的情况.根据实际调查结果显示,途经公交线路较多的公交站台在早晚高峰期间经常出现停靠4辆公交车辆的现象.因此将公交站点前50 m的区域设为公交到站区域.如果GPS的投影点在公交到站区域内,则认为公交车辆已进站,则GPS点的回传时间Tn-1即为公交车辆的到站时间Ts,将公交车停靠站的时间纳入到下一个站点区间的计算中. 情形2:GPS投影点在公交到站区域外. 研究假定在相邻的2个GPS定位数据点间公交车辆匀速行驶.当GPS投影点在公交到站区域外,则通过站点与GPS定位数据点间的位置比例关系,按照线段长度比例计算公交车辆的到站时间如式(3): (3) 式中,Ts为公交到站时间;Tn-1为第n-1个GPS点的回传时间;Tn为第n个GPS点的回传时间;Is为站点在弧段上的位置比例(%);Ia(n-1)为第n-1个GPS点的弧段位置比例(%);Ian为第n个GPS点的弧段位置比例(%);dLi为弧段编号分别表示i,j,k,g的弧段长度(m). 2.1.4 车辆上下行行驶方向判别 当成功匹配的公交站点≥2个时,判断公交站点的编号是否与车辆行驶方向相同.若相同,则输出并记录车辆信息、弧段信息和站点信息等.若方向不相同,则调换假定的车辆行驶方向,重新开始匹配公交车辆GPS数据. 表3 车辆行驶轨迹数据 2.1.5 站点区间运送速度计算 通过公交到站时间匹配流程,计算公交车辆的站点区间行程时间T,结合站点区间长度D,计算车辆运送速度V. (4) 公交车辆在站点区间的运送速度计算结果如表4所示. 2.2.1 基于速度阈值的修正 由于存在行程时间估计误差,部分速度计算值会超过合理的速度值域.考虑到公交车辆在不同等级道路上的运行特性,研究设置了针对不同道路等级的公交站点区间运送速度阈值.根据每个站点区间的道路等级,判断其速度计算结果是否超出阈值.速度阈值如表5: 表4 公交站点区间运送速度计算结果 表5 公交站点区间运送速度判别阈值与修正阈值 km·h-1 若站点间运送速度计算值超出阈值,则采取以下处理方法: 1)合并异常站点相邻2个站点区间的行程时间和站点间距,以合并后的距离和时间,计算相邻2个站点区间的运送速度. (5) 式中,V′i,V′i+1表示相邻公交站点间运送速度的修正值;Si,Si+1表示公交站点区间距离;Ti,Ti+1表示公交站点区间车辆行程时间. 2)对合并后的站点区间运送速度进行二次阈值判断.如果速度值大于相应阈值,则将计算结果修正为阈值的数值,以获取合理的公交运送速度值. 2.2.2 基于站点位置偏差的修正 公交站点位置由公交公司提供的站点坐标确定,但由于线路站点的频繁调整以及定位误差,导致实际公交站点位置与线路数据中的站点位置存在偏差,从而使到站时间计算产生误差.如图7所示,GPS点密集的区域为公交站点实际位置,其与线路数据中的站点位置有一定的偏差. 图7 站点位置偏差 鉴于站点位置偏差原因可能造成的误差,研究利用高频手持GPS设备,对线路数据中的站点位置进行修正,即携带高频手持GPS设备在公交线路的实际站点采集地理位置信息,并将采集到的位置信息替换原有的错误位置信息,以提高计算模型精度. 采用实际跟车调查的方法[13]进行模型验证,将公交运送速度模型计算结果与调查得到的公交运送速度进行对比,掌握站点区间运送速度模型的误差情况. 验证试验共获取了1 643个有效站点区间样本,涉及21条线路,108个车次,覆盖各等级道路和不同时间段,站点区间样本的分布情况如表6所示: 表6 站点区间样本分布 对调查结果进行统计分析,误差>10%的样本占据样本总量的44%,误差>20%的样本占据71%,而误差>30%的样本仅占据11%,由此可看出,绝大部分运送速度的计算结果满足精度需要,模型具有较高的准确度.调查样本的误差频率和正态分布拟合曲线如图8所示. 图8 站点区间运送速度误差分布 同时考虑不同道路等级条件下公交运送速度的差异性,研究采用平均绝对误差和平均相对误差2个指标来反映不同等级道路上站点区间运送速度计算结果的误差情况,如表7所示: 表7 不同道路等级站点区间运送速度误差分析 表7表明,不同等级道路上的站点区间速度的平均绝对误差无明显差异,平均相对误差在7%~11%左右,高速路和快速路上的站点区间速度计算结果精度最高,为92.6%.样本总体的平均绝对误差为2.36 km/h,平均精度为91.4%. 线路运送速度是指线路长度与行驶时间和停留时间之和的比值,反映线路整体的运行效率.对比试验中108个车次的线路运送速度结果显示,线路运送速度的平均相对误差为2.1%,平均绝对误差为0.75 km/h,计算模型具有较高的准确性. 研究提出了一种基于公交GPS数据的公交运送速度计算模型,以站点区间作为运送速度计算的基本单元,结合公交线路数据,进行GPS数据的匹配与修正,应用基于速度均等假设的车辆到站时间估计方法,实现了站点区间运行时间的计算,并得到公交运送速度.研究进一步分析了模型误差产生的主要因素为到站时间估计的误差和线路数据中站点位置的偏差,并对此进行了有针对性的优化,验证结果表明:站点区间运送速度的平均精度为91.4%,线路运送速度的平均精度为97.9%,平均绝对误差<2.4 km/h.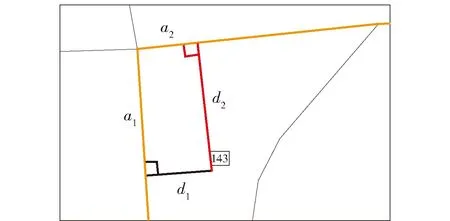


2.2 速度计算模型修正方法

3 模型验证

3.1 站点区间运送速度分析

3.2 线路运送速度分析
4 结论
