杠杆耦合式微机械陀螺仪特性分析
2020-03-12彭世刚刘海鹏高世桥李泽章
彭世刚, 刘海鹏, 高世桥,金 磊,李泽章
(北京理工大学 爆炸科学与技术国家重点实验室,北京 100081)
0 引言
微机械陀螺以其体积小,质量轻,成本低,功耗小及可批量生产等优点,在航空航天、汽车工业、医疗仪器等领域具有广泛的应用前景[1]。当前,基于科氏力的电容检测式微机械陀螺是研究的热点和应用的主流。随着研究不断深入,精度不断提升,已经实现了战术级商业应用[2-3]。随着对精度要求的不断提升,采用静电刚度调谐实现模态匹配和采用正交静电解耦实现正交解耦已成为高精度微机械陀螺的普遍措施[4],但通过文献[5-6]发现,由于与中心质量块相连的静电调谐梳齿和正交解耦梳齿在检测方向均为压膜阻尼,远大于检测框的阻尼,致使检测品质因子会严重降低,检测位移也更微弱[5-6]。近年来,杠杆放大机构在微机械传感器中已获得应用,主要用于放大驱动力,以提升微机械传感器的机械灵敏度。I.Zeimpekis等在2011年固态传感器、执行器与微系统国际会议上提出了一种用于电容式微加速度的杠杆放大机构[7];李小卿提出了一种适用于驱动模态的微机械陀螺杠杆机构,将驱动梳齿的驱动力放大传递到中心质量块上,最终使机械灵敏度提升了5.9倍[8]。然而以上的应用主要是在加速度计和微机械陀螺中进行力的放大,应用于检测模态微机械杠杆对微机械陀螺性能的影响需要进行分析。
1 杠杆位移放大结构设计
微机械陀螺仪由中心质量块、驱动模块、检测模块和弹性梁等构成。当驱动梳齿施加交变电压,中心质量块受静电力在驱动方向产生简谐振动,当z轴有角速度输入时,中心质量块受科氏力作用发生检测方向的位移,通过检测差分电容的变化敏感外界角速度的大小。
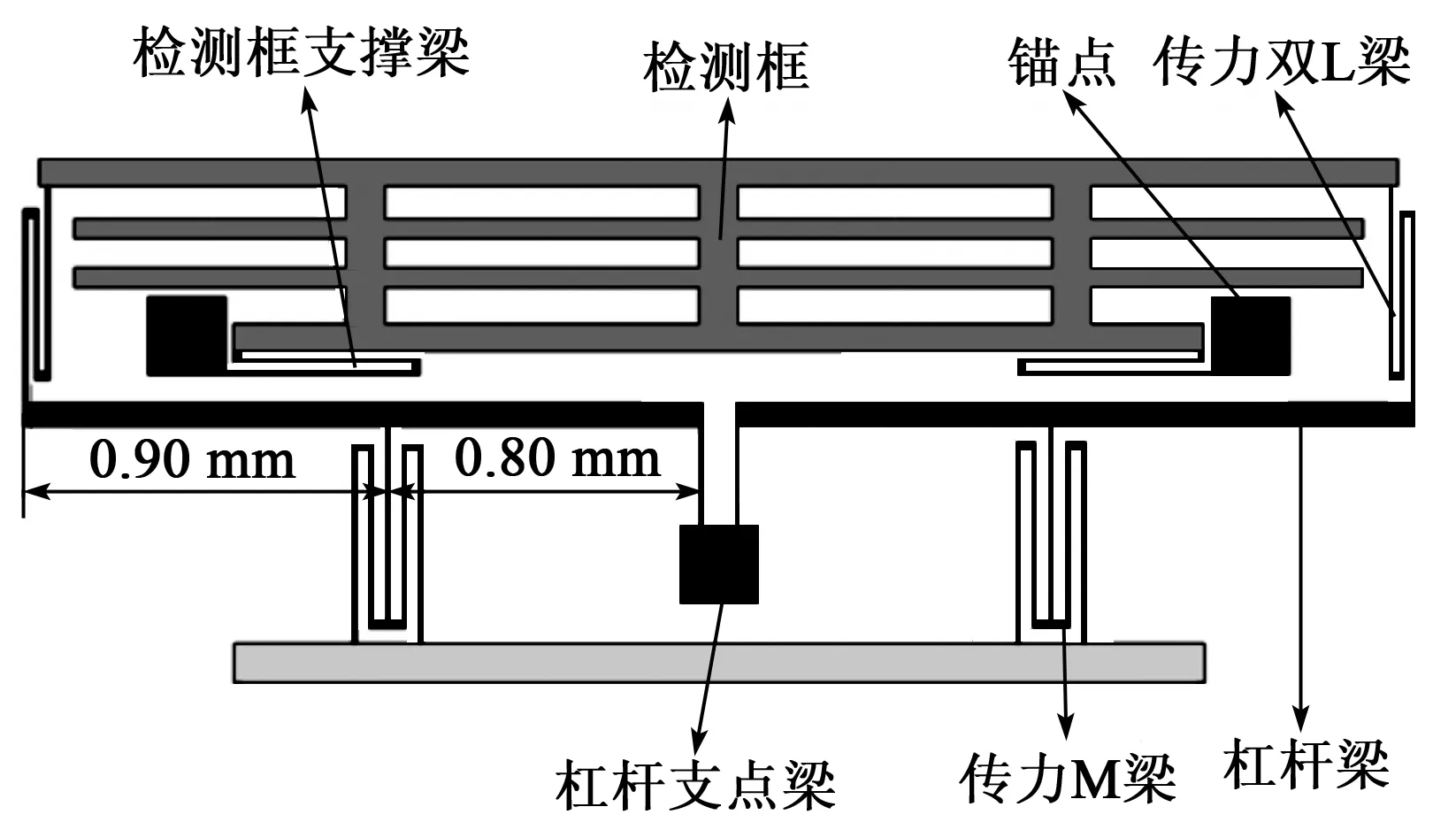
传统微机械陀螺检测模块与中心质量块通过解耦弓形梁直接耦合,然而当前电容式微机械陀螺受限于工艺条件和能力的制约,不能得到较高的精度。同时为提升硅微机械陀螺的精度,静电调谐与静电正交解耦已成为提升微机械陀螺性能的普遍方式,虽然其提升了检测准确度,但通过相关数据发现,检测品质因子会严重降低,检测位移也更微弱。曹惠亮研究发现,全对称结构陀螺品质因数在采用静电调谐和正交解耦电极后。其品质因数由均近似的5 000[5],变为驱动模态品质因数为3 820,而检测模态品质因数仅为388[6]。其主要原因是由于与中心质量块相连的调谐电极与正交解耦电极在检测方向为压膜阻尼,远大于检测梳齿的滑膜阻尼。基于此矛盾,本文创新性的提出了一种将检测模块与中心质量块通过杠杆耦合的新型结构。图1为采用杠杆耦合结构的微机械陀螺结构示意图,图2为传统直接耦合微机械陀螺结构示意图,两者除杠杆结构的区别外,其余所有机械参数均相等,以对两者的机械性能进行对比研究。
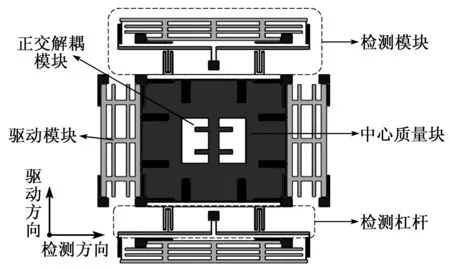
图1 杠杆耦合式微机械陀螺结构示意图

图2 直接耦合式微机械陀螺结构示意图
2 杠杆耦合式微机械陀螺机理分析
2.1 杠杆耦合式微机械陀螺动力学分析
根据杠杆耦合式微机械陀螺结构示意图,建立其两自由度振动模型,如图3所示。图中,mc为中心质量块质量,mx2为驱动模块质量,cx1为中心质量块在驱动方向上的阻尼,cx2为驱动模块阻尼,kx1为中心质量块在驱动方向上的刚度,kx2为驱动模块在驱动方向上的刚度,ms2为检测模块质量,cy1为中心质量块在检测方向上的阻尼,cy2为检测模块在检测方向上的阻尼,ky1为中心质量块在检测方向上的刚度,ky2为检测模块在检测方向上的刚度,fl11为杠杆对检测框的动力,fl12为质量块对杠杆提供的力。
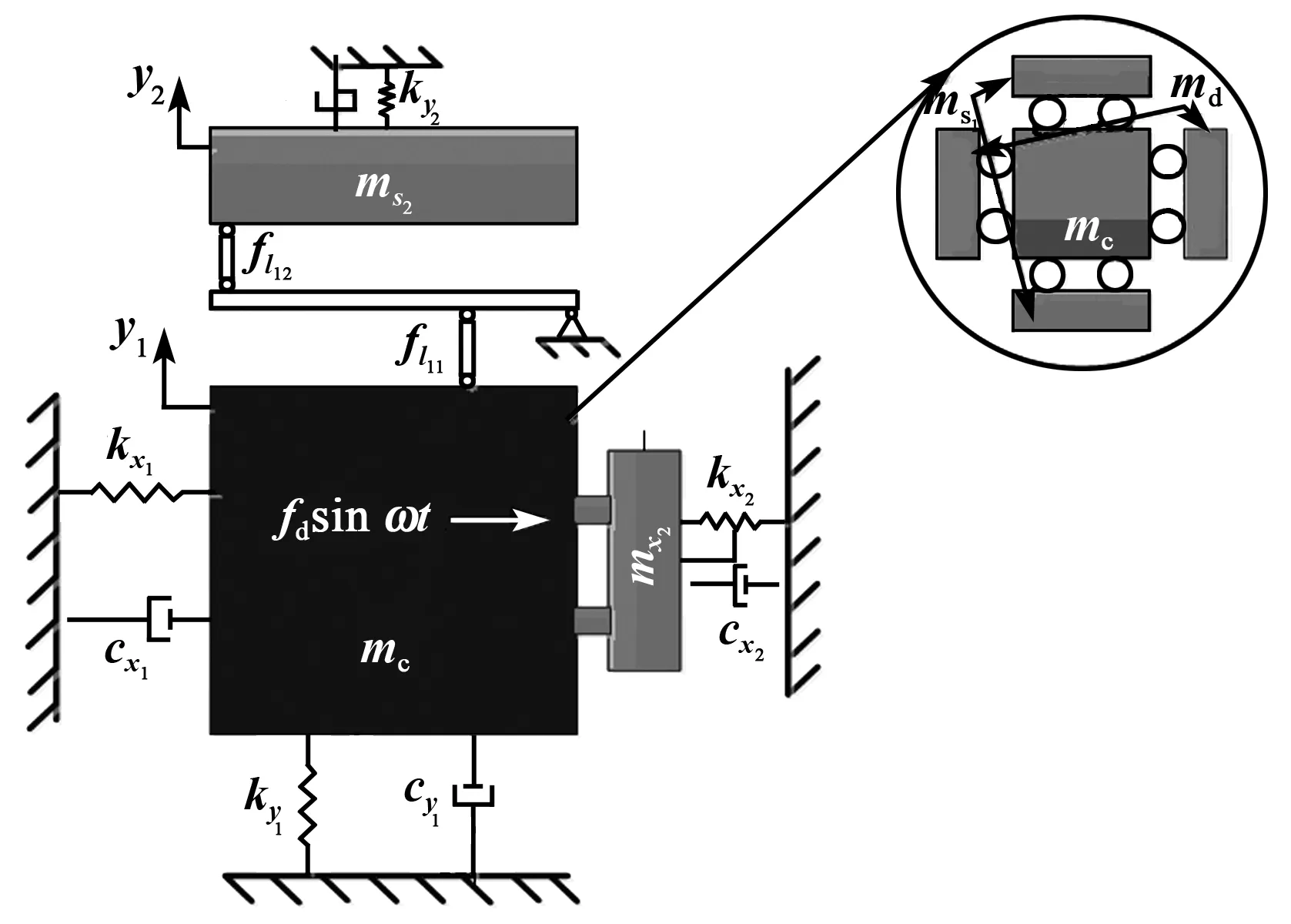
图3 杠杆耦合式微机械陀螺振动模型
杠杆耦合式微机械陀螺动力学方程为
1) 驱动方向:
(1)
式中:mx为x方向的运动总质量;kx为弹性梁在x方向上的总刚度;fd为主动驱动力,即静电力的幅值。施加杠杆前后,各分量的值不发生变化。
2) 检测方向:
(2)
式中:B为杠杆放大倍数;y1,y2分别为中心质量块和检测框的检测位移。

(3)
进一步化简为
(4)
其中
(5)
式中my,cy,ky分别为检测方向的等效质量、等效阻尼系数及等效刚度。
将式(4)化简为二阶振荡形式:
(6)
其中
(7)
(8)
式中:ωy为检测系统的固有频率;ξy为检测系统的等效阻尼比。
对式(6)求解,当谐振时,即ω=ωy=ωx,检测框的稳定位移解为
(9)
其中
(10)
式中Qy为检测系统的品质因数。
2.2 杠杆结构对微机械陀螺固有频率的影响
根据式(7)可得,有杠杆结构的微机械陀螺检测模态的固有频率为
(11)
无杠杆结构的微机械陀螺检测模态固有频率为
(12)
令ηw为检测模态固有频率比,则有
(13)

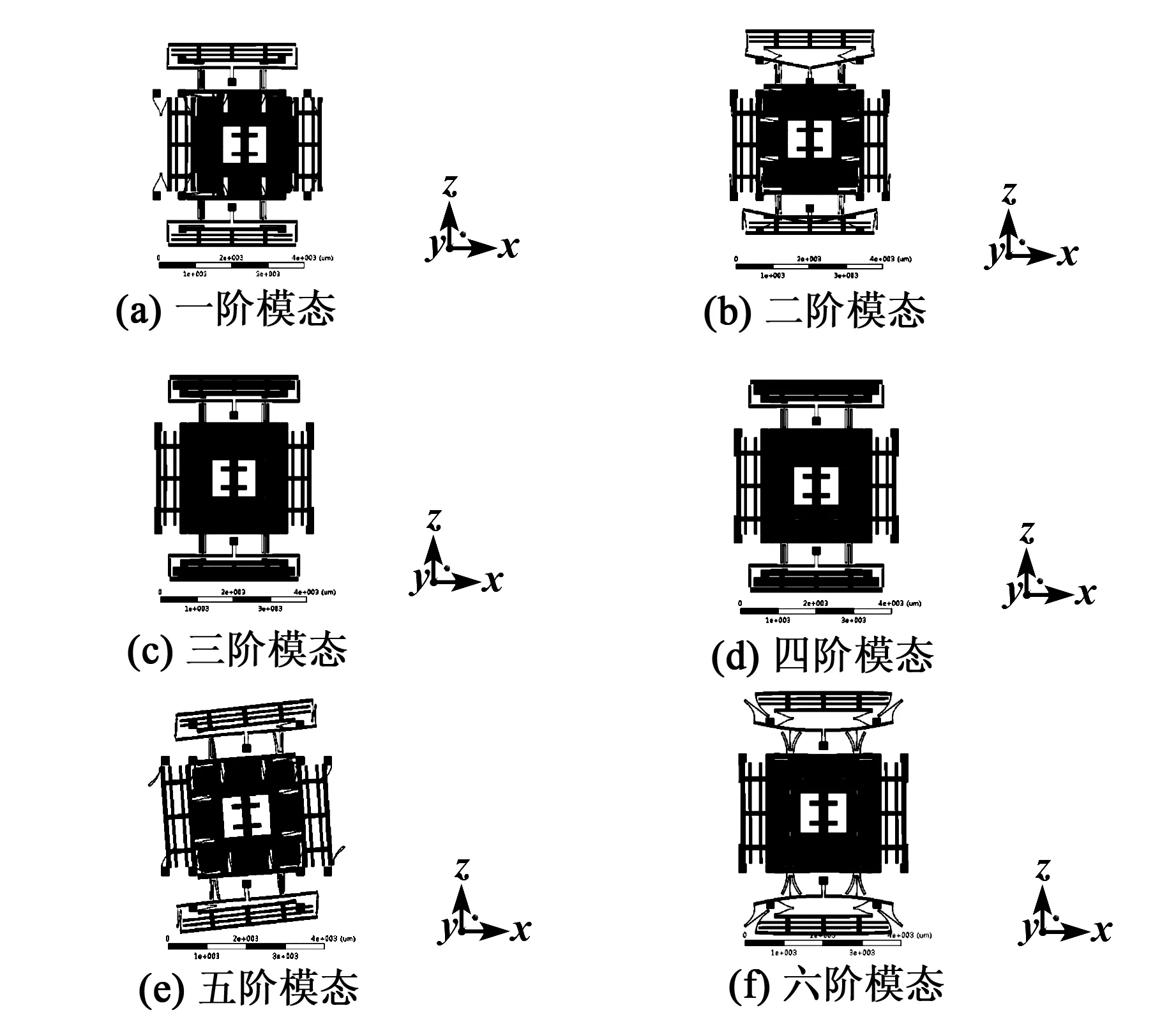
由式(13)可得,M与K为对称反比,当M>K时,位移放大杠杆可降低陀螺检测模态固有频率;当M 对比有、无杠杆检测结构的位移解。 无杠杆检测微机械陀螺的位移为 (14) 有杠杆检测微机械陀螺仪的位移为 (15) 引入位移比ηy: (16) (17) 由式(17)可得,位移放大效率由C,K,M,B4个参数决定,其中M和K由机械参数设计决定,C由机械结构和封装等共同决定,而与M、K并无直接联系,因此对式(17)分为两部分分析。 ηy(C,K,M,B)=ηy(B,C)·ηy(M,K)= (18) 1) 对ηy(B,C)求B的偏导,并令其为0, 则 (19) (20) 对式(20)求C的偏导: (21) 可得C=1时取得极小值。 2) 对ηy(M,K)在cy1≫cy2,B>1情况下进行研究: (22) 对ηy(M,K)B>1求M的偏导,并令其为0,可得 (23) 由式(23)可得,当B>1时,ηy(M,K)B>1随M的增加而增加。 对ηy(M,K)求K的偏导,并令其为0,可得 (24) 由式(24)可得,当B>1时,ηy(M,K)B>1随K的增加而减小。 通过式(22)分析可知,M与K成倒数关系。当M=K时,ηy(M,K)B>1=1;当M>K时,ηy(M,K)B>1>1;当M 通过对ηy(B,C)和ηy(M,K)的分析可得,位移放大效果主要与C和K有关,在普遍情况下,由于调谐电极和解耦电极的阻尼远大于检测梳齿的滑膜阻尼,且M>K。ηy(B,C)和ηy(M,K)的值均大于1,故杠杆能实现位移放大。 杠杆结构是该设计的关键,理想杠杆应具有无穷小的转动刚度和无穷大的拉压刚度,以此实现有较大的力传递效率。本文设计了一种柔性铰链杠杆结构,实现尽量小的力传递损耗,在符合加工工艺要求和杠杆设计原则的基础上,设计的杠杆检测模块结构如图4所示,其中B=2.125,整体厚为80 μm,杠杆检测模块结构尺寸参数如表1所示。 图4 杠杆模块结构示意图 表1 杠杆检测模块各段尺寸 通过有限元软件ANSYS对杠杆检测结构进行仿真分析,由静刚度法获得ky2=154.75 N/m。 根据微机械陀螺的结构参数可得各部分质量, 即ms2=330×10-9kg,mc=1 169×10-9kg,由my=mc+B2ms2=2 659.15×10-9(kg);驱动系统总质量为mx=1 425.1×10-9kg。 同理,计算微机械陀螺各部分结构刚度,其中ky1=840 N/m,ky2=154.75 N/m,由ky=ky1+B2ky2=1 539.78(N/m),驱动模态总刚度kx=807.1 N/m; 根据检测系统各模块的刚度与质量,由式(11)可得ωLy=3 829.76 Hz,驱动模态固有频率为3 790 Hz。 采用有限元仿真软件对微机械陀螺进行模态仿真,验证上述理论。微机械陀螺前6阶模态和振型如图5所示。 图5 杠杆耦合式微机械陀螺模态仿真图 通过模态仿真结果可知,其一阶模态为驱动模态,固有频率为3 810.7 Hz,二阶模态为检测模态,固有频率为3 810.8 Hz,与式(11)计算结果基本相等,检测模态准确率为94%,验证了关于刚度和固有频率的理论计算正确性。其差值原因可能是未考虑杠杆阻碍刚度和质量,导致计算频率高于仿真频率。驱动模态与检测模态的固有频率基本相等,可实现模态匹配,且工作模态的固有频率远高于其他模态的固有频率,符合设计要求。 为验证微机械杠杆对陀螺检测位移的放大效果,本文采用有限元仿真软件ANSYS对两个陀螺的动态谐响应进行仿真,其中一个在检测方向施加杠杆结构,另一个无杠杆结构,其余各部分的结构参数均相等。对两个陀螺施加幅值均为1 μN的科氏力,其频率为各自的谐振频率。由于两者结构参数均相等,两者的检测框阻尼系数和中间部分(包括调谐和正交解耦梳齿)阻尼均相等,且根据文献[5-6]分析,后者起主要部分,据此计算仿真阻尼比。最终检测梳齿和中心质量块的谐响应仿真结果如图6所示,仿真参数如表2所示。 图6 微机械陀螺谐响应仿真值 表2 结构仿真参数 杠杆耦合陀螺直接耦合陀螺施力幅值/μN1 1施力频率/Hz3 805~3 8174 262~4 279中间部分阻尼88×10-9检测梳齿阻尼 11×10-9 由图6可知,杠杆耦合陀螺在谐振下的最大位移为0.67 μm,带宽为8 Hz。而直接耦合陀螺在谐振下最大位移为0.418 μm,带宽为11 Hz,其检测梳齿位移放大比为1.601。根据式(18)理论计算值1.744,准确率为91.9%,验证了杠杆检测位移放大理论的准确性。同时可看出检测梳齿与中心质量块位移比为2.22,大于B,这可能是在该频率下检测框形成局部共振引起的,但其具体机理需进一步分析。 设计了一种基于柔性杠杆的位移放大微机械陀螺。通过二阶振动动力学模型分析了杠杆结构对微机械陀螺特性的影响机理。分析表明,杠杆结构通过改变陀螺的结构静刚度与等效质量,从而改变陀螺的固有频率值。进一步分析了陀螺检测位移的谐响应值,即放大效率与杠杆放大倍数和结构参数的关系。通过仿真实例验证,杠杆结构能改善结构的固有谐振频率,在由于静电调谐电极等结构导致检测梳齿的阻尼小于其余部分阻尼的情况下,能显著提升检测位移,进而提升检测精度,对今后微机械陀螺的设计与制作具有较好的指导意义。2.3 杠杆结构对陀螺检测模态谐响应的影响
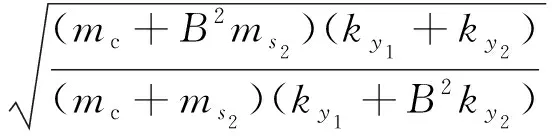

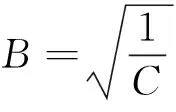
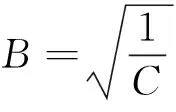
3 仿真分析
3.1 杠杆结构设计与仿真
3.2 微机械陀螺模态分析
3.3 微机械陀螺谐响应分析


4 结束语
