基于毕达哥拉斯TODIM和Heronian算子的语言多属性群决策及应用

岳小云，毛学志，刘思严，杨晓静，邱凤霞

(河北科技师范学院数学与信息科技学院，河北 秦皇岛，066004)

模糊集的概念最早是由Zedah[1]提出的，一代又一代的学术研究者们付出了努力，加速了模糊集理论的不断完善，促使直觉模糊集理论的产生，该理论是由Atanassov[2]提出。由于直觉模糊集在实际应用中的某些情况不满足适用条件，于是Yager[3]定义了毕达哥拉斯模糊集(Pythagorean Fuzzy Set)及集结算子。Zhang[4]研究了TOPSIS方法在毕达哥拉斯模糊集环境下的应用。Yang[5]针对文献[4]中定理3.4存在的缺陷，提出了新定理及证明过程。范建平等[6]提出了毕达哥拉斯模糊交叉熵，并用交叉熵代替距离测度，提高了结果的准确性。杜玉琴[7]定义了毕达哥拉斯梯形模糊语言集及其集结算子，并以企业挑选绿色供应商问题为例验证方法实用性。李进军等[8]研究了区间毕达哥拉斯模糊集的三类Hamming距离。施明华等[9]和李素勤[10]均提出，在毕达哥拉斯模糊集环境下的多属性群决策的应用。在属性和专家权重均未知情形下，Wan等[11～13]拓展相对距离公式、确信度、信息熵和LINMAP方法于毕达哥拉斯模糊群决策，并应用于风险投资、绿色供应链和雾霾治理决策。另外，考虑到决策有限理性，Gomes[14]提出了TODIM方法。自TODIM方法提出以来，许多学者扩展到直觉模糊集、多值中智集和犹豫模糊语言集[15～17]。为此，笔者在决策信息为毕达哥拉斯模糊环境下改进TODIM方法，进而运用PF-TODIM方法研究语言多属性群决策问题，以此解决远程会诊协同质量评估问题。

1 预备知识

1.1 毕达哥拉斯模糊集

定义1[18]设X是一个论域，则毕达哥拉斯模糊集(PFNs)定义为：

P=〈〈x,P(μp(x),vp(x))〉|x∈X〉

(1)

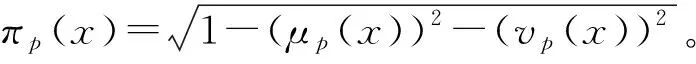
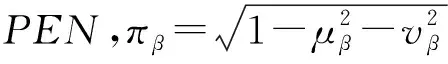
为了更好的运用毕达哥拉斯模糊集，给出毕达哥拉斯模糊集的运算与性质。

定义2[18]给定3个PENsβ1=〈μ1,v1〉,β2=〈μ2,v2〉和β=〈μ,v〉，基本运算有

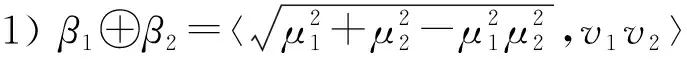
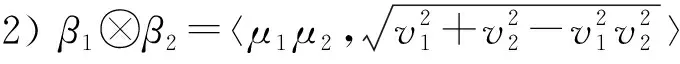
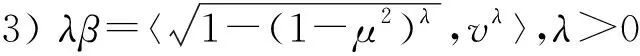
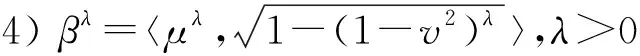
5)β1∧β2=〈min{μ1,μ2},max{v1,v2}〉

6)β1∨β2=〈max{μ1,μ2},min{v1,v2}〉

7)βc=〈v,μ〉

定义3[19]对于PENβ=〈μβ,vβ,πβ〉，β的得分函数定义

(2)

其中-1≤Sc(β)≤1。

定义4[19]设β1=〈μ1,v1,π1〉和β2=〈μ2,v2,π2〉是2个PFNs，β1和β2的得分函数分别为Sc(β1)和Sc(β2)，则

1) 当Sc(β1)〉Sc(β2)，有β1优于β2，记为β1≻β2；

2) 当Sc(β1)〈Sc(β2)，有β1劣于β2，记为β1β2；

3) 当Sc(β1)=Sc(β2)，有β1等于β2，记为β1=β2。

定义5设β1=〈μ1,v1,π1〉和β2=〈μ2,v2,π2〉是2个PFNs，β1和β2之间距离为

(3)

1.2 毕达哥拉斯模糊集的集结算子

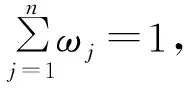
(4)

(5)

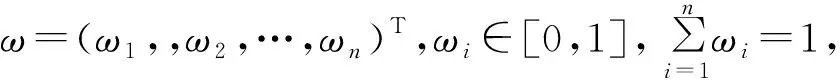
(6)

则称PFWGHM算子为毕达哥拉斯加权几何Heronian算子。

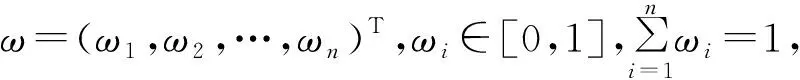
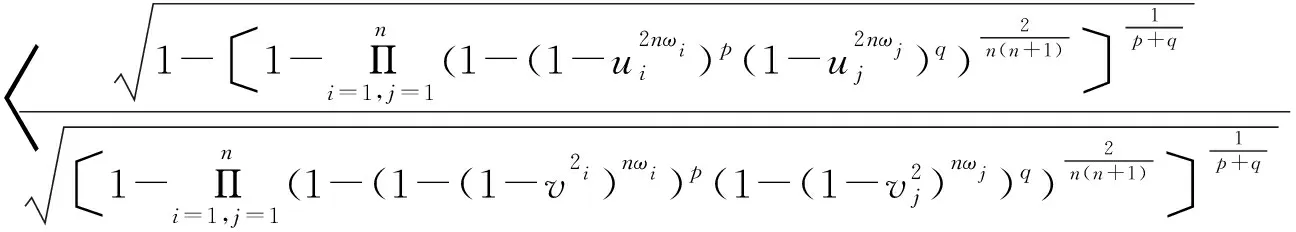
(7)

容易证明PFWGHM算子具有下列性质：

性质1(幂等性)如果所有的i,αi=〈ui,vi〉相等，记αi=α(i=1,2,…,n)，则

PFOWGHM(α1,α2,…,αn)=α

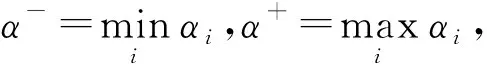
α-≤PFWGHM(α1,α2,…,αn)≤α+

性质3(单调性)设αi=〈ui,vi〉(i=1,2,…,n)和αi′(i=1,2,…,n)两组PFNs，如果对任意i，有αi≤αi′，则PFWGHM(α1,α2,…,αn)≤PFWGHM(α1′,α2′,…,αn′)。

定义8设p与q为不同时为0的非负实数，αi=〈ui,vi〉(i=1,2,…,n)为PFN，若有

(8)

则称PFOWGHM算子为毕达哥拉斯加权几何Heronian算子，其中αi′表示αi(i=1,2,…,n)中的第i(i=1,2,…,n)大的PFN，权重向量为

n为常数，g∶[0,1]→[0,1]为一个BUM函数，并满足g(0)=0,g(1)=1以及若x>y则g(x)≥g(y)。

定理2设p与q为不同时为0的非负实数，αi=〈ui,vi〉(i=1,2,…,n)为PFN，由PFOWGHM算子集结得到的值也是PFN，且

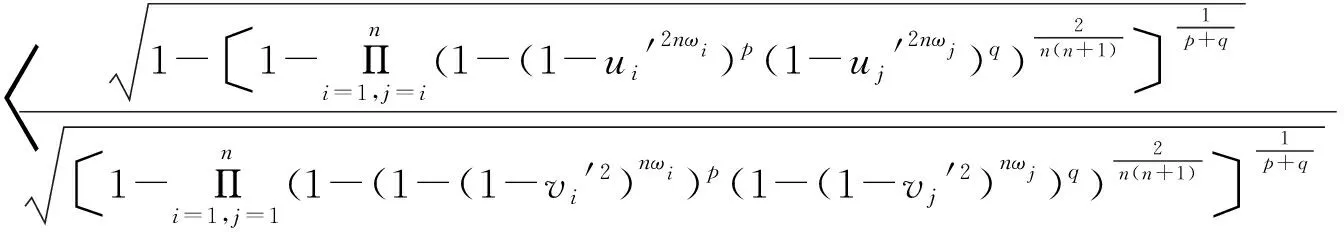
(9)

容易证明PFOWGHM算子有下列性质：

性质1(幂等性)如果所有的i，αi=〈ui,vi〉相等，记αi=α(i=1,2,…,n)，则

PFOWGHM(α1,α2,…,αn)=α

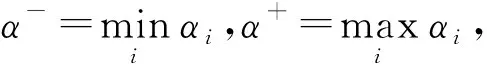
α-≤PFOWGHM(α1,α2,…,αn)≤α+

性质3(单调性)设αi和αi′(i=1,2,…,n)为2组PFNs，如果对任意i，有αi≤αi′，则

PFOWGHM(α1,α2,…,αn)≤PFOWGHM(α1′,α2′,…,αn′)

2 基于PFN的语言多属性群决策模型

2.1 多属性群决策问题描述

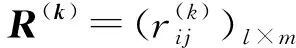
2.2 改进TODIM方法

TODIM方法是通过计算总优势度和总前景值对备选方案进行优选或排序。方法中，关键是优势度的确定，具体如下:

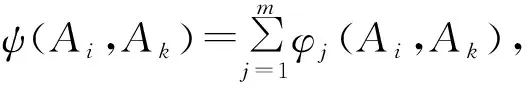
(10)

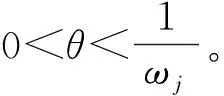
2) 计算方案Ai的总前景值ζi，这里

(11)

TODIM方法依据总前景值越大，可行方案越优原则。选择最理想的可行方案或对所有备选方案进行排序。总前景值最大的可行方案是最可取的。相反，具有最小值的可行方案是最差的。

2.3 模型建立

为了有效地处理2.1部分的针对决策信息和属性权重由语言术语表示的多属性群决策问题，下面利用PF-TODIM方法进行研究，该方法的关键在于考虑了决策者的有限理性。

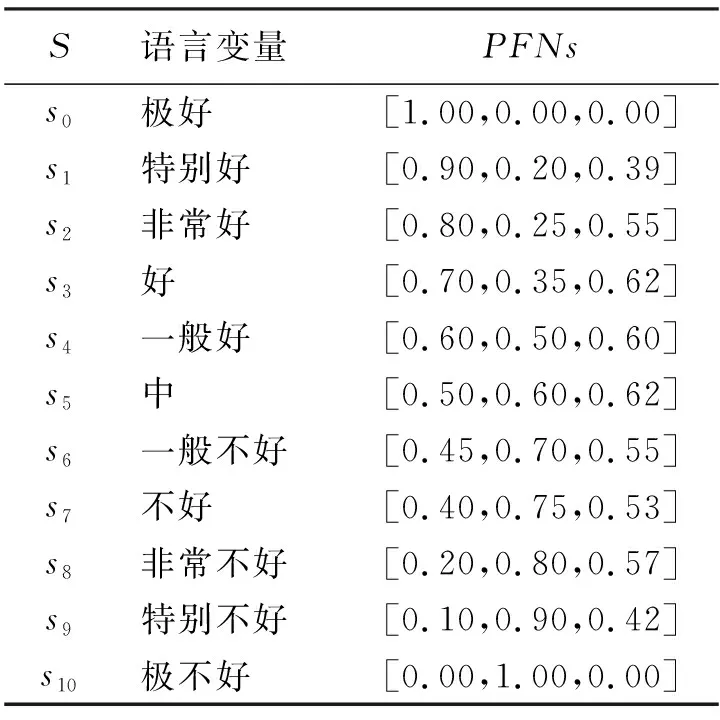
表1 语言变量与PFNs对应关系

(12)

由决策组εk(k=1,2,…,n)给出属性Cj(j=1,2,…,m)的语言权重为ω=(ω1,ω2,…,ωn)T，属性权重最终通过表2来转化。

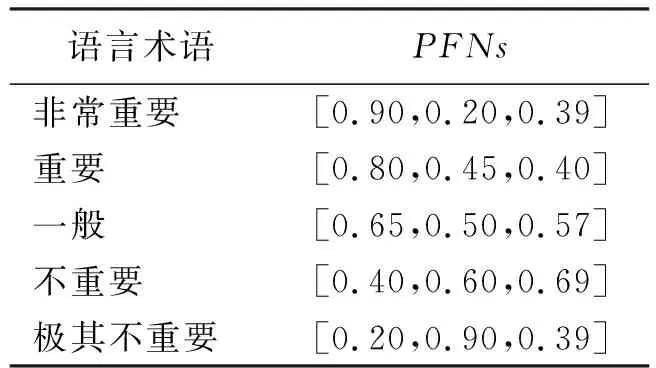
表2 语言术语与的对应关系

步骤2群决策矩阵的集结。群决策中，决策者εk(k=1,2,…,n)给出决策权重为σk(k=1,2,…,n)。所有决策者的决策信息通过PFWGHM算子进行集结，记为χ=(xij)l×m，其中

xij=(uAi(Cj),vAi(Cj),πAi(Cj)),i=1,2,…,l；j=1,2,…,m

相应地，χ=(xij)l×m表示为：

(13)

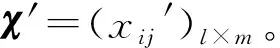
步骤5取θ=2.25，利用式(11)～式(13)计算TODIM方法中的优势度ψ(Ai,Ak)(i,k=1,2,…,l)和前景值ζi(i=1,2,…,l)。

步骤6对所有可行方案进行排序。依据总前景值ζi越大，方案Ai越优，确定最优方案。

3 实例和对比分析

3.1 实例分析

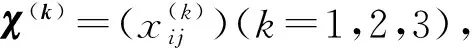
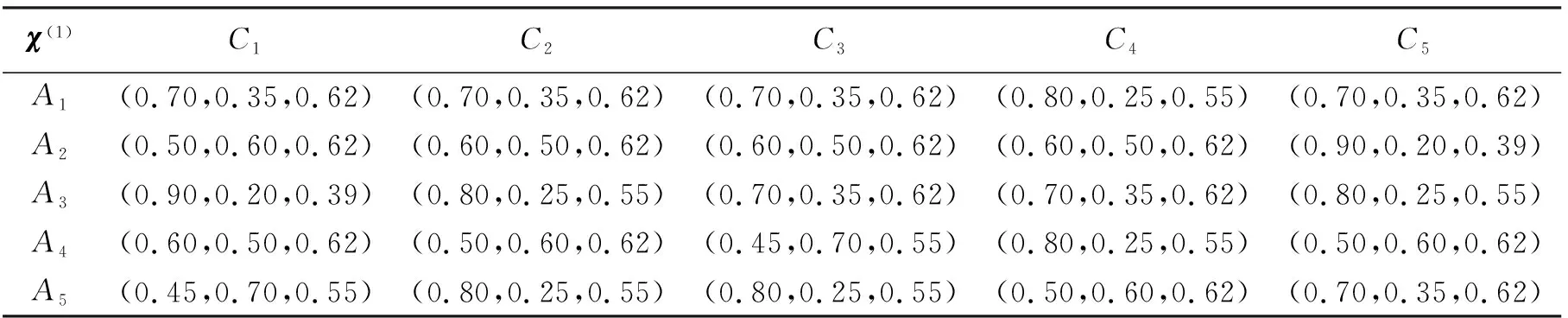
表3 第1类决策组决策矩阵

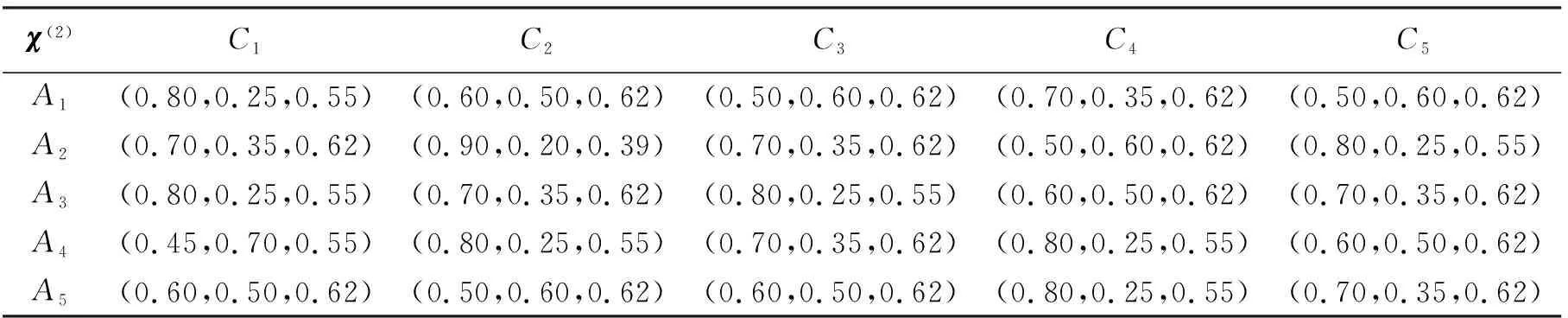
表4 第2类决策组决策矩阵

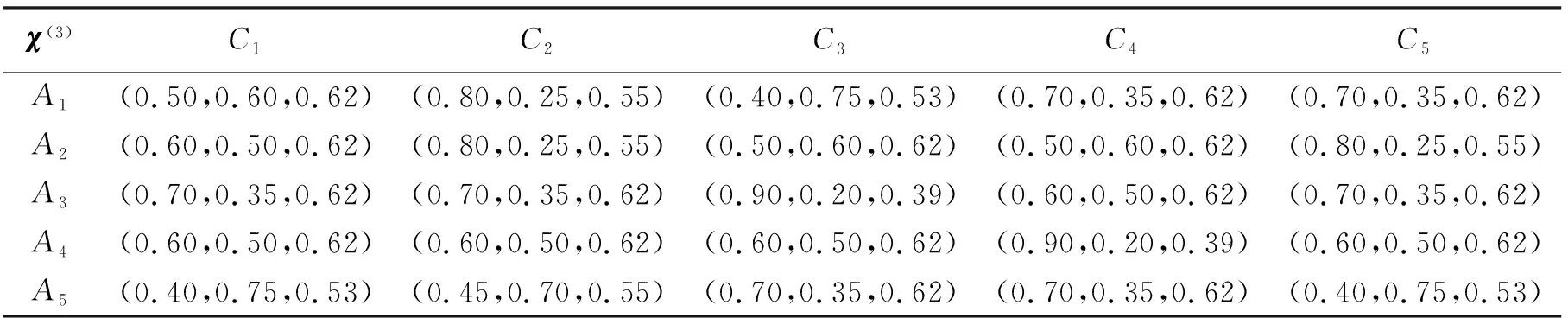
表5 第3类决策矩阵

步骤1利用算子集结为PEN-群决策矩阵，得出

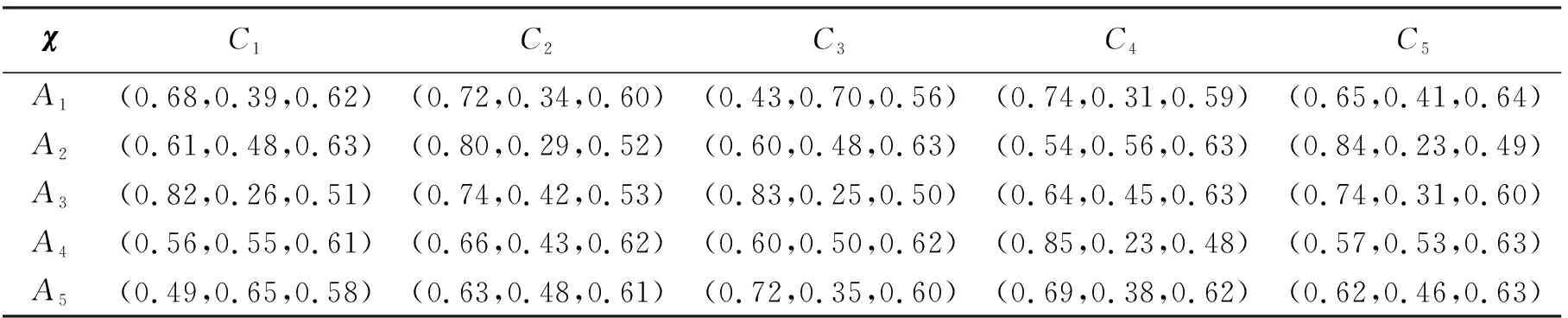
表6 PFN-群决策矩阵

步骤2由于C1，C2，C3，C4是效益型属性，而C5是成本型属性， 表6转化为表7。

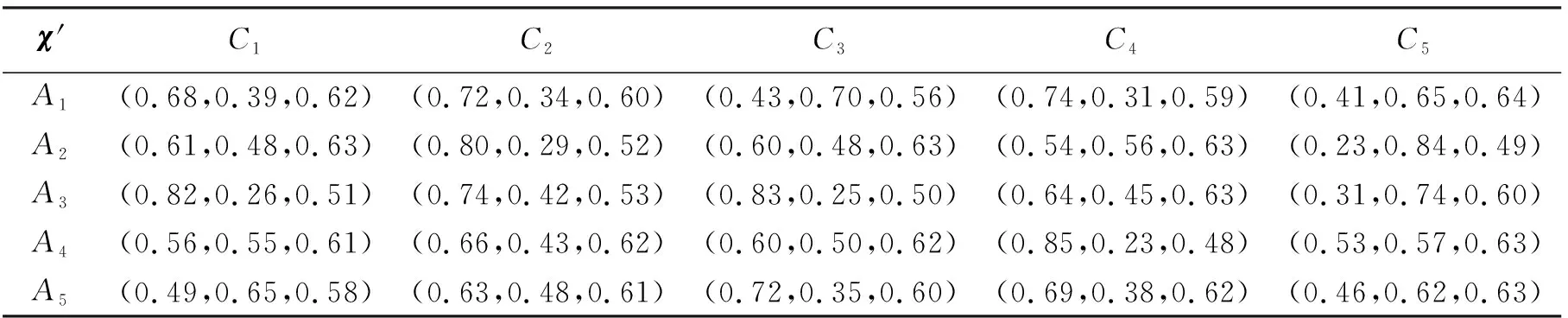
表7 规范化毕达哥拉斯群决策矩阵

步骤3属性权重的确定。结合表2中语言术语和毕达哥拉斯模糊数(PFNs)之间的关系，给出属性权重信息如表8，由集结算子式(5)、得分函数和权重性质计算得属性权重ω：ω1=0.20,ω2=0.10,ω3=0.25,ω4=0.23,ω5=0.21。

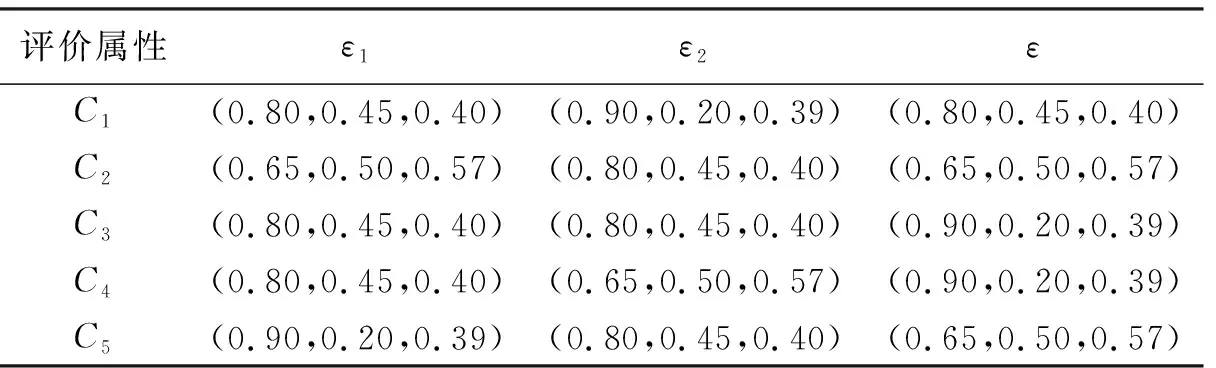
表8 PFNs表示的属性权重信息

步骤4通过式(10)计算方案Ai相对方案Ak的总优势度，结果见(表9)。

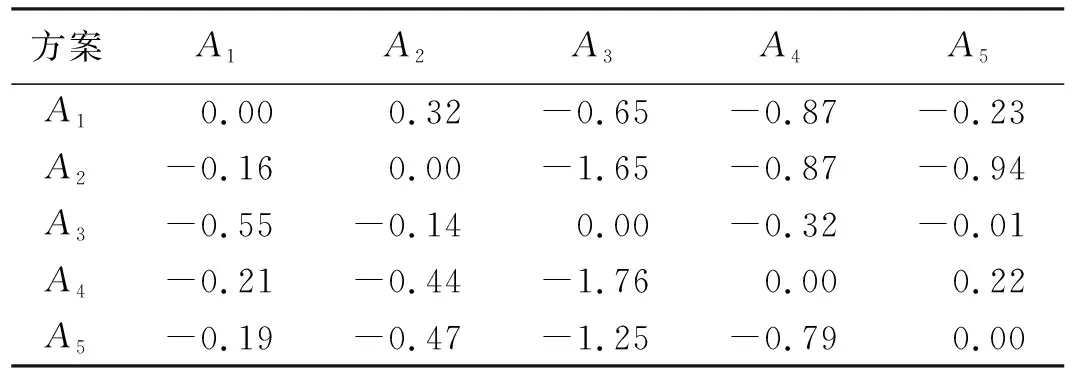
表9 方案Ai相对方案Ak的总优势度

步骤5利用式(11)计算方案A1的前景值A1=0.59，A2=0.00，A3=1.00，A4=0.55，A5=0.35。根据方案前景值越大方案越优的原则，对所有备选方案进行从优到劣排序，结果为：A3≻A1≻A4≻A5≻A2。

3.2 对比分析

笔者利用文献[11～13]中涉及的方法对3.1节实例进行分析。文献[11]采用毕达哥拉斯模糊TOPSIS方法进行备选方法优选排序，文献[12]采用基于毕达哥拉斯相对贴近度和交叉信息熵的群决策方法，文献[13]采用基于毕达哥拉斯相对距离和信息可能度的群决策方法。结果表明，毕达哥拉斯模糊TODIM方法和文献[11～13]中得到的排序结果有些不同(表10)，笔者采用的毕达哥拉斯模糊TODIM方法得到的A1≻A4，而文献[11～13]得到的是A4≻A1。导致不一致的原因在于笔者本次研究考虑了决策者的心理行为因素，而文献[11～13]是在决策者完全理性的情况下决策的。在现实中，对于不完整的信息或其他一些因素，决策者通常不能提供准确的偏好。也就是决策者在某种程度上是不合理的。毕达哥拉斯模糊TODIM方法可以合理地描述决策者在风险下的心理行为，从而有效地处理上述问题。

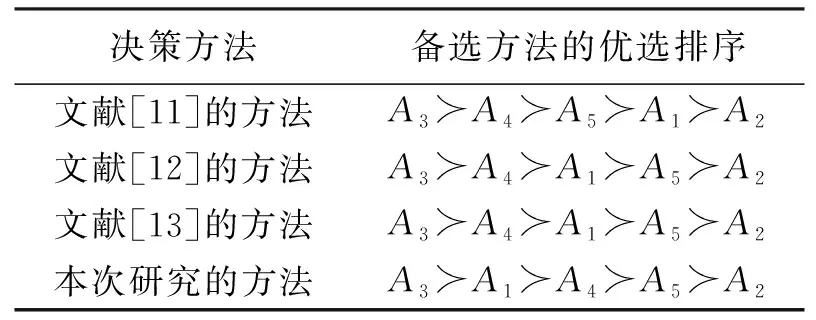
表10 多属性群决策方法比较

4 结论与讨论

由于毕达哥拉斯模糊集比直觉模糊集更易于处理现实世界中的模糊信息，笔者采用毕达哥拉斯模糊集探讨了语言多属性群决策问题。首先，由于决策有限理性，借助得分函数等改进TODIM的总优势度，进而适用于毕达哥拉斯决策环境，拓展了TODIM的适用范围。其次，考虑到Heronian算子具有优良的性质，比如捕获变量之间的关联性，结合Heronian算子建立毕达哥拉斯模糊群决策方法，使集结信息更加准确合理。最后，该方法应用到远程会诊协同服务质量的评价中，进一步验证了该方法的合理性和有效性。该方法有望应用于其他群决策环境，如工业工程、应急决策、商业管理等。对于TODIM方法，属性权重的准确与否至关重要，今后应进一步探讨毕达哥拉斯模糊决策中属性权重的确定方法。