完全二部图K10,n(215≤n≤466)的点可区别E-全染色
2020-03-12包丽娅陈祥恩王治文
包丽娅,陈祥恩*,王治文
(1.西北师范大学数学与统计学院,甘肃 兰州730070;2.宁夏大学数学统计学院,宁夏 银川750021)
0 引言
关于图的点可区别全染色已有许多研究[1-4]。图G的一个E-全染色f是指使相邻点着以不同的色,且任意一个顶点与它的关联边着以不同颜色的全染色。设f为G的一个E-全染色,如果对任意的互不相同的顶点u,v∈V(G),有C(u)≠C(v),那么称f为图G的点可区别E-全染色,简称为VDET 染色。令{k|G存在k-VDET 染色},称为图G的点可区别E-全色数。
文献[5]探讨了星、轮、扇、路、圈、完全图,完全二部图K2,n的VDET 染色。文献[6]得到mC3和mC4的VDET 色数。文献[7-9]讨论了完全二部图K3,n,K4,n,K5,n的VDET 染色。文献[10]讨论了完全二部图K7,n的VDET 染色。文献[11-12]讨论了完全二部图K10,n的VDET 染色。本文主要讨论K10,n(215≤n≤466)的VDET 染色,并 得到了K10,n(215≤n≤466)的VDET 色数。
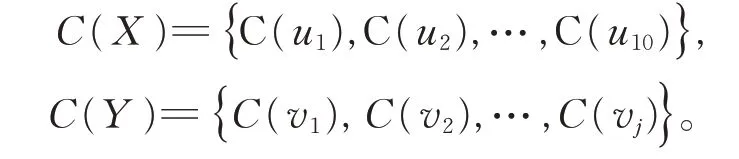
引理1[11]当10≤n≤90时,有
引理2[12]当91≤n≤214时,有
引理3[12]K10,214存在一个9-VDET 染色:X中顶点u1,u2,…,u10的色集合分别为顶点u1,u2,…,u10的颜色分别为1,2,1,2,1,2,2,2,1,2,Y中顶点的色集合分别为{1,2,3,4,5,6,7,8}的7-子集、6-子集、5-子集、4-子集、3-子集、2-子集,但不是前面已经出现的X中顶点的色集合,不是含1 或含2的2-子集,不是{5,6},{1,5,6},{2,5,}6 ,{1,2,5,6},也不是同时含1和2的3-子集。
1 主要结果及证明
定理1当215≤n≤466时,有
证明先证K10,n不存在8-VDET 染色。假设K10,n有8-VDET 染色f,所用颜色为1,2,…,8。考虑下面7种情形。
情形1u1,u2,…,u10的颜色当中互不相同的仅有1种。不妨设f(ui)=1,i=1,2,…,10,则每个C(vj)不包含颜色1,从而可以作为Y中顶点色集合{1,2,3,4,5,6,7,8}的子集数目为当215≤n≤466时,128个集合不能区分Y中的n个顶点,矛盾。
情形2u1,u2,…,u10的颜色当中互不相同的仅有2种。不妨设f(ui)∈{1,2},i=1,2,4,…,10。则当C(vj)是2-子集时,C(vj)不包含颜色1 或2,从而可以作为Y中顶点色集合的{1,2,3,4,5,6,7,8}的子集的数目为当235≤n≤466时,234个集合不能区分Y中的n个顶点,矛盾。
下设215≤n≤234。令B=B1∪B2∪B3,C(Y)⊂B,其中,

B3是{1,2,3,4,5,6,7,8}的4-子集、5-子集、6-子集、7-子集、8-子集和不在B2中的3-子集构成的集合。
发现B中包含i的成员有120个,i=1,2;B中包含j的成员有125个,j=3,4,…,8。因此,每个C(ui)至少包含3种颜色,故C(X)⊆B2∪B3,C(X)∪C(Y)⊂B,有10+n≤234,n≤224,因此,当225≤n≤466时,B中的成员不能区分Y中的n个顶点,矛盾。
以下仅考虑当215≤n≤224时的情况。即B1中至多有9个集合不是Y中顶点的色集合,从而每个C(ui)至少同时包含3,4,…,8中的某2种色,i=1,2,…,10。
情形2(a)B2中至少有1个成员是Y中顶点的色集合,可得1,2 ∈C(ui),i=1,2,…,10。
(i)C(ui)恰好 同时包含3,4,…,8中的某2种色,不妨设3,4 ∈C(ui),i=1,2,…,10,则{5,6},{5,7},{5,8},{6,7},{6,8},{7,8}均不是Y中顶点的色集合,从而10+n≤234-6,n≤218。当219≤n≤466时,218个集合不能区分Y中的n个顶点,矛盾。
以下仅考虑当215≤n≤218时的情况。此时{1,5,6},{1,5,7},{1,5,8},{1,6,7},{1,6,8},{1,7,8}至多有3个不是Y中顶点的色集合。如果{1,5,6},{1,5,7},{1,5,8},{1,6,7},{1,6,8},{1,7,8}都是Y中顶点的色集合,则5,6,7,8中至少有3种色同时包含在每个顶点颜色为1的点的色集合,不妨设5,6,7 ∈C(ui),f(ui)=1。此时{2,5,6},{2,5,7},{2,5,8},{2,6,7},{2,6,8},{2,7,8}中至多有3个不是Y中的顶点色集合,可得5,6,7,8中至少有1种色同时包含在每个顶点颜色为2的点的色集合中,设a∈C(ui),f(ui)=2,其中a∈ {5,6,7,8}。若{a}∩{5,6,7}=∅,则a=8,从而每个C(ui)只能是以下集合之一:矛盾。
若{a}∩{5,6,7}≠∅,则颜色{a}∩{5,6,7}同时包含在每个C(ui)中,与假设矛盾。
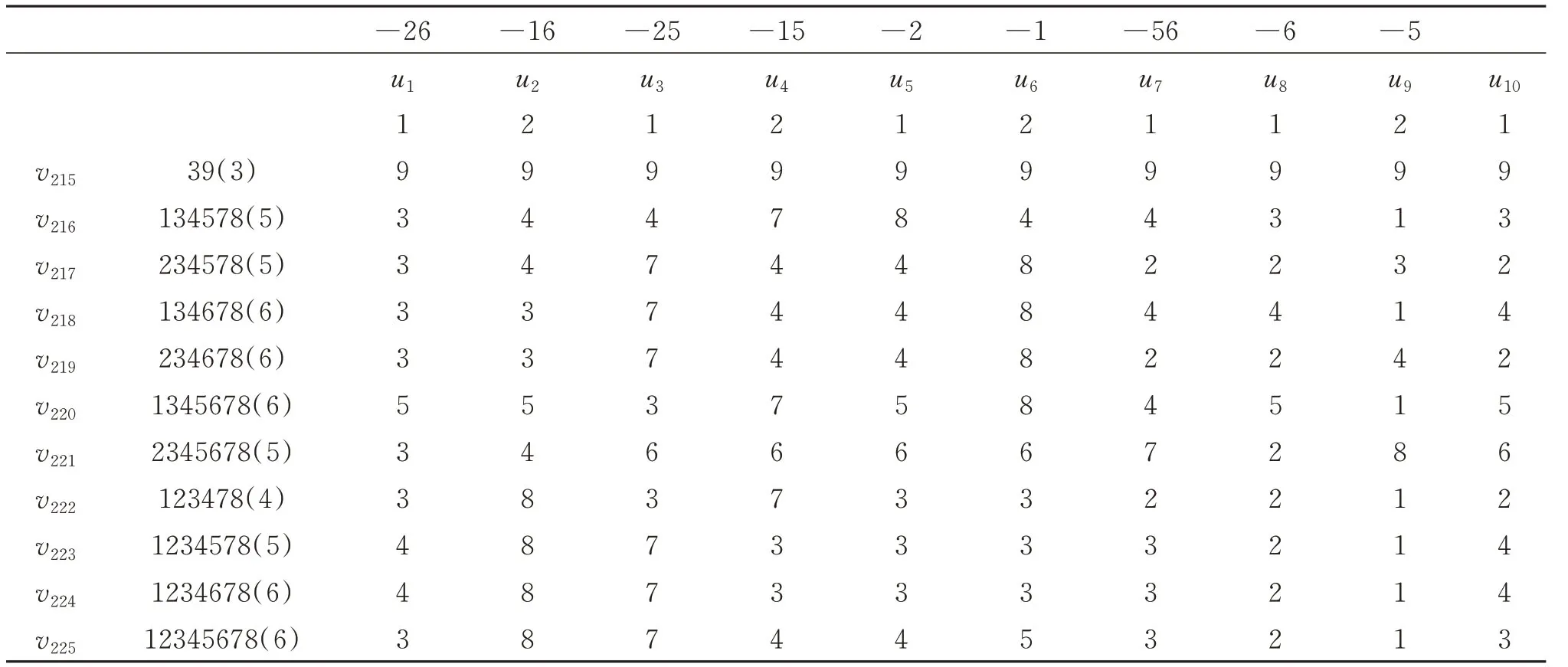
如果{1,5,6},{1,5,7},{1,5,8},{1,6,7},{1,6,8},{1,7,8}恰有1个或2个不是Y中顶点的色集合,则5,6,7,8中至少有2种色同时包含在每个顶点颜色为1的点的色集合中,不妨设5,6 ∈C(ui),f(ui)=1;此时中至多有2个不是Y中顶点的色集合,从而5,6,7,8中至少有2种色同时包含在每个顶点颜色为2的点的色集合中,设a,b∈C(ui),f(ui)=2,其中,a 如果{1,5,6},{1,5,7},{1,5,8},{1,6,7},{1,6,8},{1,7,8}中恰有3个不是Y中顶点的色集合,可得5,6,7,8中至少有1种色同时包含在每个顶点颜色为1的点的色集合中,设a∈C(ui),f(ui)=1,其中a∈{5,6,7,8}。此时{2,5,6},{2,5,7},{2,5,8},{2,6,7},{2,6,8},{2,7,8}都是Y中顶点的色集合,可得5,6,7,8中至少有3种色同时包含在每个顶点颜色为2的点的色集合中,不妨设当f(ui)=2时,5,6,7 ∈C(ui)。若{a}∩{5,6,7}=∅,则a=8,从而每个C(ui)只能是以下集合之一 :矛盾。 若{a}∩{5,6,7}≠∅,从而每个C(ui)同时包含颜色{a}∩{5,6,7},与假设矛盾。 (ii)C(ui)至少同时包含3,4,…,8中的某3种色,不妨设3,4,5 ∈C(ui),i=1,2,…,10,从而每个C(ui)只能是以下集合之一:8个集合不能区分X中的10个顶点,矛盾。 情形2(b)B2中成员均不是Y中顶点的色集合。 (i)C(ui)恰好 同时包含3,4,…,8中的某2种色,不妨设3,4 ∈C(ui),i=1,2,…,10。则{5,6},{5,7},{5,8},{6,7},{6,8},{7,8},{1,2,3},{1,2,4},{1,2,5},{1,2,6},{1,2,7},{1,2,8}均不是X和Y中顶点的色集合,从而10+n≤234-12,有n≤212,212个集合不能区分Y中的n个顶点,矛盾。 (ii)C(ui)恰好同时包含3,4,…,8中的某3种色,不妨设3,4,5 ∈C(ui),i=1,2,…,10。因此{6,7},{6,8},{7,8}不是Y中顶点的色集合,且B2中成员均不是X中顶点的色集合。从而10+n≤234-9,n≤215。当216≤n≤466时,215个集合不能区分Y中的n个顶点,矛盾。 以下仅考虑n= 215时的情形。此时均是Y中某顶点的色集合。由于{1,6,7},{1,6,8},{1,7,8}均是Y中顶点的色集合,则每个顶点颜色为1的点的色集合至少同时包含6,7,8中的某2种色,不妨设当f(ui)=1时,6,7 ∈C(ui);由 于{2,6,7},{2,6,8},{2,7,8}均是Y中顶点的色集合,则每个顶点颜色为2的点的色集合至少同时包含6,7,8中的某2种色,不妨设当f(ui)=2时,a,b∈C(ui),其中a (iii)C(ui)恰好同时包含3,4,…,8中的某4种色,不妨设3,4,5,6 ∈C(ui),i=1,2,…,10。因此{7,8}不是Y中顶点色集合,且B2中成员均不是X中顶点的色集合。从而10+n≤234-7,n≤217。当218≤n≤466时,217个集合不能区分Y中的n个顶点,矛盾。 以下仅考虑当215≤n≤217时的情形。此时中存在1个是Y中某顶点vj0的色集合。不妨设f(vj0)=8,所以每个C(ui)包含{1,2},{1,7},{2,7} 3个集合之一。从而每个C(ui)只能是以下集合之一:矛盾。 (iv)C(ui)至少同时包含3,4,…,8中某5种色,不妨设3,4,5,6,7 ∈C(ui),i=1,2,…,10,从 而每个C(ui)只能是集合之一,6个集合不能区分X中的10个顶点,矛盾。 情形3u1,u2,…,u10的颜色当中互不相同的仅有3种,不妨设f(ui)∈{1,2,3},i=1,2,…,10。则当C(vj)是2-子集时,C(vj)不包含颜色1,2 或3,且每个C(vj)都不是{1,2,3},从而可以作为Y中顶点色集合的{1,2,3,4,5,6,7,8}的子集的数目为,故当229≤n≤466时,228个集合不能区分Y中的n个顶点,矛盾。 下设215≤n≤228。令C=C1∪C2∪C3,C(Y)⊂C,其中, C3是{1,2,3,4,5,6,7,8}的4-子集,5-子集,6-子集,7-子集,8-子集和不在C2∪{{1,2,3}}中的3-子集构成的集合。 发现C中包含i成员的有119个,i=1,2,3;C中包含j成员的有123个,j=4,5,6,7,8。因此每个C(ui)至少包含3种色,C(X)∪C(Y)⊂C∪{{1,2,3}},10+n≤228+1,n≤219。从而当220≤n≤228时,219个集合不能区分Y中的n个顶点,矛盾。 以下仅考虑当215≤n≤219时的情形。此时C1中至多有4个成员不是Y中顶点的色集合,因此4,5,6,7,8中至少有2种色同时包含在每个C(ui)中,不妨 设4,5 ∈C(ui),i= 1,2,…,10。故{1,2,3}不是X中任意一个顶点的色集合,C2中成员均不是X中点的色集合,且至多有4个不是Y中点的色集合,因此可推出1,2,3 ∈C(ui),i=1,2,…,10。从而每个C(ui)只能是以下集合之一 :矛盾。 情形4u1,u2,…,u10的颜色当中互不相同的仅有4种,不妨设f(ui)∈{1,2,3,4},i=1,2,…,10。则当C(vj)是2-子集时,不含颜色1,2,3 或4,且每个C(vj)也都不是{1,2,3},{1,2,4},{1,3,4},{2,3,4},设Y中顶点色集合为D,从而可以作为Y中顶点色集合的{1,2,3,4,5,6,7,8}的子集的数目为当221≤n≤466时,220个集合不能区分Y中的n个顶点,矛盾。 以下仅考虑当215≤n≤220时的情形。发现D中包含i的成员有116个,i=1,2,3,4。D中包含j的成员有119个,j=5,6,7,8。因此每个C(ui)至少包含3种色,故 因此,有10+n≤220+5,可得n≤215。从而当216≤n≤220时,215个集合不能区分Y中的n个顶点,矛盾。 以下仅考虑当n=215时的情形。此时{5,6},均是Y中顶点的色集合,可得5,6,7,8中至少有3种色同时包含在每个C(ui)中,不 妨 设 5,6,7 ∈C(ui),i=1,2,…,10。因此,均不是X中顶点的色集合,从而有10+n≤220,n≤210。210个集合不能区分Y中n个顶点,矛盾。 情形5u1,u2,…,u10的颜色当中互不相同的仅有5种,不妨设f(ui)∈{1,2,3,4,}5 ,i=1,2,…,10。则当C(vj)是2-子集时,只能是{6,7},{6,8},{7,8},且每个C(vj)也都不是{1,2,3,4,}5的3-子集,4-子集,5-子集,从而可以作为Y中顶点色集合的{1,2,3,4,5,6,7,8}的子集的数目为206个集合不能区分Y中的n个顶点,矛盾。 情形6u1,u2,…,u10的颜色当中互不相同的仅有6种,不妨设f(ui)∈{1,2,3,4,5,}6 ,i=1,2,…,10。则当C(vj)是2-子集时,只能是{7,8},且每个C(vj)也都不是{1,2,3,4,5,6}的3-子集,4-子集,5-子集,6-子集,从而可以作为Y中顶点色集合的的子集数目为178个集合不能区分Y中的n个顶点,矛盾。 情形7u1,u2,…,u10的颜色当中互不相同的仅有 7种,不 妨 设f(ui)∈{1,2,3,4,5,6,}7 ,i=1,2,…,10。则每个C(vj)不可能是2-子集,每个C(vj)也都不是{1,2,3,4,5,6,}7的3-子集,4-子集,5-子集,6-子集和7-子集,从而可以作为Y中顶点色集合的{1,2,3,4,5,6,7,8}的子集的数目为120个集合不能区分Y中的n个顶点,矛盾。 表1 K10,466 顶点vj(215≤j≤225)及其关联边的染色方案Table1 The coloring method of vertex vj and its incident edges ofK10,466 when 215≤j≤225 表2 K10,466 顶点vj(226≤j≤466)及其关联边的染色方案Table2 The coloring method of vertex vj and its incident edges of K10,n when 226≤j≤466 因此,K10,n没有8-VDET染色,且 当215≤n≤466时,χevt(K10,n)≥9。 下面给出K10,n的一个9-VDET 染色。 首先确定f466。X中顶点u1,u2,…,u10的色集合分别为 顶点u1,u2,…,u10的颜色分别为1,2,1,2,1,2,2,2,1,2。 将X∪{v1,v2,}v3,…,v214所导出的K10,466的子图按照引理3 给出的8-VDET 染色f214进行染色,然后染其他的顶点和关联边。 将vj(215≤j≤225)和它的关联边按表1的方式进行染色(表1的第1行表示顶点ui(1≤i≤10)的色集合,第2行表示顶点ui(1≤i≤10)的颜色,第3 行的39(3)表示顶点v215着色3,顶点v215的色集合为{3,9},顶点v215的关联边u1v215,u2v215,…,u10v215分别着色9,9,9,9,9,9,9,9,9,9,依此类推)。 将顶点vj(226≤j≤466)分别对应色集合{1,2,3,4,5,6,7,8,9}的全体含颜色9的2-子集,3-子集,4-子集,5-子集,6-子集,7-子集,8-子集,但不是{1,2,9}、{3,9},也不是表1X中任意一个顶点的色集合。顶点vj(226≤j≤466)和它的关联边u1vj,u2vj,…,u10vj的具体染色方案见表2。当215≤j≤466时,K10,466的9-VDET 染 色f466在由X∪{v1,v2,…vj}所导出的子图上的限制显然是K10,j的9-VDET 染色fj。 先利用反证法和分析法得到了当215≤n≤466时,用8种颜色不能对K10,n进行点可区别E-全染色。因此,当215≤n≤466时,χevt(K10,n)≥9。然后利用构造染色法,说明了用9种颜色可以对K10,n进行点可区别E-全染色,从而得到其VDET 色数为9。继续研究了当n≥467时的K10,n的VDET染色。在后续研究中,利用反证法、分析法以及构造染色法,讨论并给出了相应的VDET 色数,由于证明过程较长,此证略。
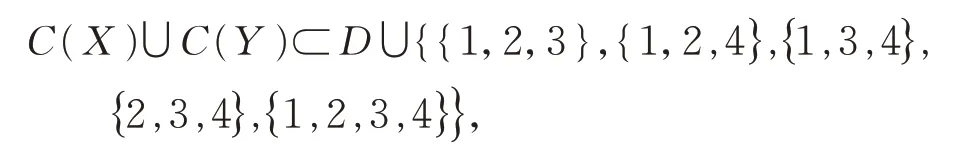


2 结 语
