基于有限元法的心墙砾石土压实特性分析

2020-03-12王毓杰王佳俊

水力发电 2020年12期

崔博，王毓杰，王佳俊，余佳

(天津大学水利工程仿真与安全国家重点实验室，天津300350)

0 引言

砾石土料经过压实后有较高的密度和强度以及较好的防渗性能，目前作为填筑材料广泛应用于高心墙土石坝中[1]。严格控制现场施工工艺以保证砾石土压实质量，其中，碾压作业是心墙砾石土施工的关键环节，开展压实特性(物理特性和变形特性)研究对于控制碾压施工质量有着非常关键的作用[2-3]。在碾压过程中，高振状态使砾石土产生较大的塑性变形，碾轮与砾石土的接触面不断变化，导致砾石土的压实特性也发生了显著变化，准确把握砾石土压实特性的变化对控制心墙砾石土的压实质量有着重要的研究意义。

碾压过程中，由于振动荷载下土体塑性变形的滞后性和碾轮与土体接触面的不确定性，碾轮与土体的动力相互作用表现出材料非线性、几何非线性和接触非线性[4]。采用传统的静力学或者动力学理论分析时会很复杂繁琐，且难以得到精确的解析结果，因此需采用数值模拟方法对这类问题进行数值分析。数值模拟是揭示土体压实机理的重要方法，目前已成功应用于沥青路面[3，5-6]、碾压混凝土[7]、黄土[8]、堆石体[9]、宕渣[10]等领域[11-14]的压实研究。从以上研究可知，利用数值模拟方法通过分析土体的压实特性、力学响应以及各种因素对压实效果的影响等方面，能够有效地研究土体在碾压过程中的压实行为，不过尚未发现数值模拟方法在砾石土压实特性的相关研究。

砾石土是由一定级配的岩石颗粒和土料组成的无凝聚性土石混合体[15]。乔兰、Xiao等[16-17]对砾石土进行室内击实试验，分析了在击实作用下砾石土的颗粒破碎规律，并分析了砾石土压实特性的变化规律；李朝政、冯瑞玲等[18-19]通过室内击实试验和现场碾压试验结合确定砾石土的碾压参数，以此控制工程施工质量。同时，近年来一些学者也利用数值模拟方法来研究土石混合体的物理力学特性。王鹏飞等[20]对土体混合体进行数值模拟，从含石量、块石空间分布方面来研究其力学特性的变化；崔博等[21]基于离散元法进行土石混合体的三轴数值模拟试验，对其力学性质进行研究。从上述分析可知，砾石土的压实特性大多数是通过室内击实试验开展相关研究，并且通过现场碾压试验确定碾压参数；而数值模拟方面的研究是通过结合三轴压缩与离散元法研究其力学性质。

国内外研究中，尚未发现将振动凸块碾与心墙砾石土结合起来作为耦合体系研究碾压过程中砾石土体压实特性的变化；同时，考虑到现场试验有耗资大、试验工作量大、周期长及数据离散型性高等缺陷，因此有必要在传统试验工作的基础上，引入数值模拟的手段来弥补室内和现场试验方面的不足。由于凸块碾与砾石土相互作用时存在复杂的非线性关系以及砾石土有非均质性和各向异性等复杂工程性质，目前没有精确的本构关系来描述其力学特性。ABAQUS作为有限元计算分析软件的代表，具有良好的非线性解析功能和收敛性，常用于求解各种复杂材料的非线性问题，而且具有能真实反映土体复杂性状的本构模型，易于处理砾石土这类土石混合料的非均质性和各向异性问题。

本文基于有限元法，构建“凸块碾-砾石土”三维有限元模型，以研究心墙砾石土的压实特性。首先，根据现场碾压的振动凸块碾尺寸，将振动凸块碾简化为碾轮并建立其有限元模型；其次，确定砾石土的模型尺寸、本构模型以及基本参数以构建砾石土的三维有限元模型；再者，通过“凸块碾与砾石土”模型的接触分析，模型作用荷载的施加进行模型的仿真计算，并与实测值对比证明该模型的可行性；最后，从沉降量、竖向应力幅值、密度等方面研究碾压过程中砾石土的压实特性，分析砾石土的应力分布规律，为心墙砾石土的压实质量研究提供科学的理论依据。

1 “凸块碾-砾石土”三维有限元模型

1.1 建立振动凸块碾模型

振动凸块碾是一种作用力组合式的压实机械，是将振动平碾、凸块的压实原理进行复合，在其碾压滚筒上有多排矩形塔状凸块，按滚筒轴线交错布置。振动凸块碾在碾压过程中不仅借助碾轮重力与激振力的作用，同时也借助凸块插入土体时使土体受到挤压和揉搓的联合作用，从而使土体达到良好的压实效果。本文研究的凸块碾机械参数、砾石土模型参数、碾压试验数据资料均依托于西南某高心墙堆石坝工程，其中凸块碾模型为心墙碾压中的三一重工26 t自行式振动凸块碾，其机械参数如表1所示。

表1 凸块碾机械参数

由于振动凸块碾碾压心墙砾石土时，主要是其碾轮部分对砾石土有压实作用，综合前人振动压实数值模拟的相关研究[9-10]，加之考虑到其结构的复杂性，也为了减少计算量，将振动凸块碾简化为碾轮，利用ABAQUS建立光滑碾轮模型和凸块模型。将建立好的碾轮模型和凸块模型导入到SolidWorks软件进行排列装配，再将其导入到ABAQUS得到凸块碾模型如图1所示。由于碾轮相对土体而言刚度很大，而且也并非研究对象，将其视为刚体，不参与变形计算。

图1 振动凸块碾模型示意

1.2 建立砾石土模型

砾石土体属于半空间结构，前后左右及下方是无限延伸的，在进行有限元分析时可取长方体砾石土块来代替理论上的半空间结构[22]。在接触表面除外的5个面(四个侧面和底面)上施加固定边界约束，并将砾石土有限元模型分为2层，上层为碾压层，厚30 cm；下层为已压实的下垫层，厚25 cm，与现场施工情况吻合。

根据现场碾压作业的施工情况，凸块碾在碾压心墙砾石土时行驶速度要严格控制在2～3 km/h，碾轮的直径是1.7 m，当凸块碾以最低速度2 km/h滚动行驶时，滚动一周所需的时间最长，经计算最大周期9.048 s。

为了模拟砾石土在整个周期内的碾压过程，必须使碾压一遍的仿真时间大于最大周期9.048 s，因此本文模型在模拟心墙砾石土的碾压施工时，碾压一遍仿真时间选取为10 s。由于凸块碾的碾轮宽度为2.17 m，可将砾石土模型宽度设为2.5 m，本文仿真中凸块碾的最高行驶速度为3 km/h，仿真时间为10 s，则模型所需最短长度8.3 m，将模型长度设为10 m。本文的砾石土模型分为两层，上层为碾压层，模型长10 m、宽2.5 m、高0.3 m，下层为压实后的下垫层，模型长10 m、宽2.5 m、高0.25 m，得到砾石土模型如图2所示。

图2 砾石土模型示意

针对砾石土本构模型的选取，由徐鼎平等[23]的研究可知Mohr-Coulomb模型能够有效表达砾石土在受压作用下的应力-应变关系，因此本文选取ABAQUS里面的Mohr-Coulomb模型进行模拟，模型初始的各项计算参数见表2。

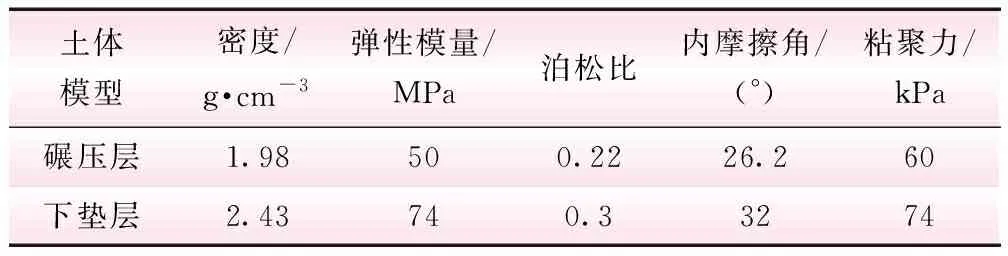
表2 砾石土模型参数

1.3 模型接触作用分析

砾石土在凸块碾的滚动过程中受到碾轮凸块的挤压和揉搓作用，加上凸块碾的振动作用使其力学性能不断发生变化，加上凸块碾与砾石土在碾压过程中接触面积的变化导致二者之间存在复杂的非线性问题。ABAQUS中解决非线性线性问题的求解器包括ABAQUS/Standard和ABAQUS/Explicit，对于高速复杂的非线性行为应用ABAQUS/Explicit求解器较高效准确。凸块碾与砾石土存在复杂的接触行为且凸块碾的振动频率较高，故本文选择ABAQUS/Explicit求解器进行有限元计算分析。对于存在复杂拓扑关系的模型之间的接触分析，考虑到碾压过程中凸块碾对砾石土的挤压和揉搓作用导致接触面不断发生变化，从而产生非线性接触，因此需要使用通用接触来施加接触。通用接触可以通过软件自动分析模型来定义模型之间的接触关系，从而节约时间成本。

接触属性包括3方面：法向作用、切向作用和阻尼作用。法向作用是在“凸块碾-砾石土”模型中，当凸块碾与砾石土不发生接触行为时，二者之间不存在拉应力，故选取硬接触；切向作用为利用静-动摩擦指数衰减形式来定义接触面的切向摩擦，该摩擦模型还需定义弹性滑移刚度，假设碾压过程中不存在滑移现象，故弹性滑移刚度设为无限大；阻尼作用为接触阻尼力在法向方向上与滑移率成比例，在切向方向与弹性滑移率成比例，切向阻尼的定义是通过定义其和法向阻尼系数的比值来定义的，ABAQUS/Explicit中默认该比值大小为1。

1.4 模型作用力

振动碾压过程中，“凸块碾-砾石土”模型施加的荷载为

P=G+F

(1)

F=F0sin(ωt)

(2)

式中，P为砾石土的作用力；G为机械自重；F0为激振力；F为F0的分力；ω为振动频率；t为时间。

“凸块碾-砾石土”模型施加作用力后如图3所示。

图3 模型作用力示意

1.5 “凸块碾-砾石土”有限元模型验证

在振动压实过程中，随着土体不断地被压实，土体的相关特性参数也在不断发生变化。根据前人关于振动压实数值模拟的研究，有学者[22]通过改变不同遍数下的模型参数来进行模拟碾压过程，也有学者[3，13]考虑到压实前与压实后的模型参数变化不大，假设模型参数不变的情况下采用初始的模型参数来进行模拟碾压过程，均取得了不错的效果。本文采取这2种方式对“凸块碾-砾石土”模型进行模拟，一方面能验证该模型的可行性，另一方面为后续的研究奠定了基础，结合现场试验数据资料得到相应的模型参数见表3。将实测的沉降量与模拟计算得到的沉降量进行对比，对比结果见图4，其中模拟曲线1为模型参数改变时沉降量的模拟结果曲线，模拟曲线2为模型参数不变时沉降量的模拟结果曲线。

表3 模型参数

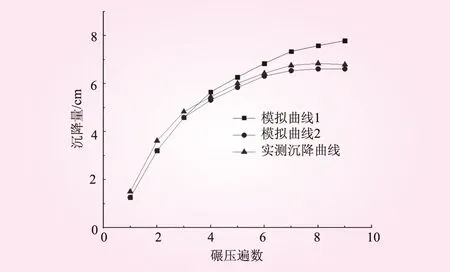
图4 模拟结果与实测沉降曲线对比

由图4可知，3条曲线的沉降量随碾压遍数的变化基本上保持一致，即初始状态下沉降量增加较快，随着碾压遍数的增加，沉降量逐渐趋于稳定。可以明显看出，模型参数不变时，与实测的沉降量曲线的变化规律较为吻合，而模型参数改变时的沉降量与实际沉降量数值上相差较大。模拟曲线1与实测值的总沉降误差为1 cm，此时的总沉降的相对误差为14.7%，最大相对误差为16%，最小相对误差为3.67%；模拟曲线2与实测值的总沉降误差为0.18 cm，此时总沉降的相对误差为1.47%，最大相对误差为16%，均满足数值模拟的要求[7]，说明基于有限元法构建的“凸块碾-砾石土”有限元模型研究心墙砾石土的压实过程是可行的。模拟曲线1与实际沉降曲线相差较大是由于砾石土压实后与压实前的模型参数变化并不是很大，改变模型参数在高强度的激振力作用下模型进行有限元数值计算时，砾石土仍会产生少量竖向位移，不同模型参数下产生的竖向位移不断叠加，这才导致了模拟曲线1相较于模拟曲线2与实测沉降的总沉降误差较大；而在模型参数不变时，凸块碾的振动作用使砾石土在前期产生较大变形，随着碾压遍数的增加，变形会逐渐减小并趋于稳定，与实测沉降的变化规律也比较相符。综上，本文假定模型的初始参数不变进行“凸块碾-砾石土”有限元模型的数值模拟。

2 基于“凸块碾-砾石土”模型的砾石土压实特性分析

2.1 沉降量分析

为了更加细致地了解砾石土沉降量在碾压过程中的变化情况，本文将“凸块碾-砾石土”模型网格划分出来的单元结点进行编号，通过分析压实轨迹中心处某观测点的沉降量在各结点对应的不同深度随时间的变化曲线，以了解不同深度处的沉降量变化情况。图5是对土体中心横向剖切得到的结点图，在图中选取该观测点沿碾压层土体深度方向(即Y轴方向)一条直线上的4个结点，分别是13 881(Y=0 cm)、35 088(Y=10 cm)、34 889(Y=20 cm)、6 120(Y=30 cm)。图6为各结点竖向位移的时程曲线。图7为各结点沉降量随碾压遍数的变化曲线。

图5 横向剖面结点

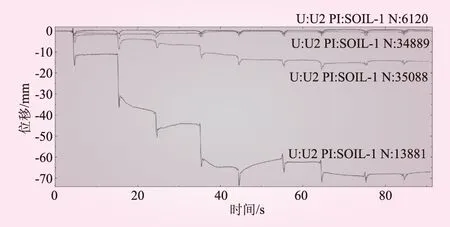
图6 各结点沉降量时程曲线

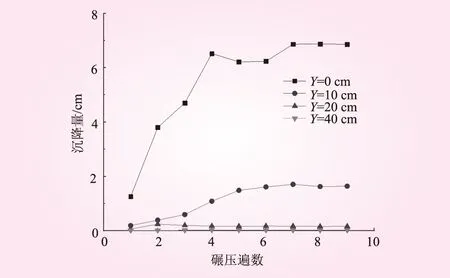
图7 不同深度的沉降量随碾压遍数变化曲线

由图6可知，该处土体在接近5 s时受到振动凸块碾的冲击作用。由于碾压一遍的周期为10 s，随后时间每增加10 s左右都要受到振动凸块碾的冲击作用，该时刻结点13 881处砾石土受到的冲击效果最强烈，结点13 881处土体的沉降量最大，在随后0.5 s左右的时间内出现少许回弹，此后该结点土体在周期内的沉降量基本上逐步趋于稳定。

综合图6和图7可以看出，结点13 881处被碾压第1遍后(5 s左右)、第2遍后(15 s左右)、第3遍后(25 s左右)和第4遍后(35 s左右)，该结点土体沉降量上升幅度比较大，随后随着碾压遍数的增加，当碾压到第7遍时，累积的沉降量逐步稳定在6.9 cm左右，且第8遍与第7遍的沉降差小于0.1 cm，说明此时土体已经达到较高的密实状态；结点35 088沉降量的变化规律和表层结点13 881一样，不过小于土体表面发生的沉降量，最终的沉降量在1.6 cm左右；而结点36 459和结点6 695随着碾压遍数的增加，沉降量也只是毫米级(即在10 mm以内)，尤其是结点6 695由于离振动源最远，沉降量已经趋近于0。

此外，由砾石土的表面沉降量变化规律可以看出，在心墙砾石土的碾压过程中，前期砾石土沉降量的增加速率较快，随着碾压遍数的增加，沉降量的增加速率慢慢减小，土体并逐渐趋于稳定状态；从图中也可以明显的看出砾石土的主要沉降量发生在土体表层部分(0～10cm)，土体产生的沉降量沿着深度方向会越小，受到冲击作用后土体回弹的位移也在沿着深度方向不断变小，这说明碾压过程中凸块碾产生的压实能量传递到土体内部时，会沿着深度方向不断减少，从而导致砾石土的沉降量也会沿着深度方向逐渐递减。

2.2 竖向应力幅值分析

振动凸块碾和心墙砾石土在碾压过程中产生了复杂的动态响应问题，从而使砾石土产生动压应力信号，动压应力信号包含相应的压实信息。采用砾石土的竖向应力幅值(砾石土受到振动冲击力时产生的竖向动压应力最大值)来揭示碾压过程中砾石土压实效果的变化规律。图8、图9分别为竖向应力幅值随碾压遍数、土体深度的变化曲线。

图8 竖向应力幅值-遍数曲线

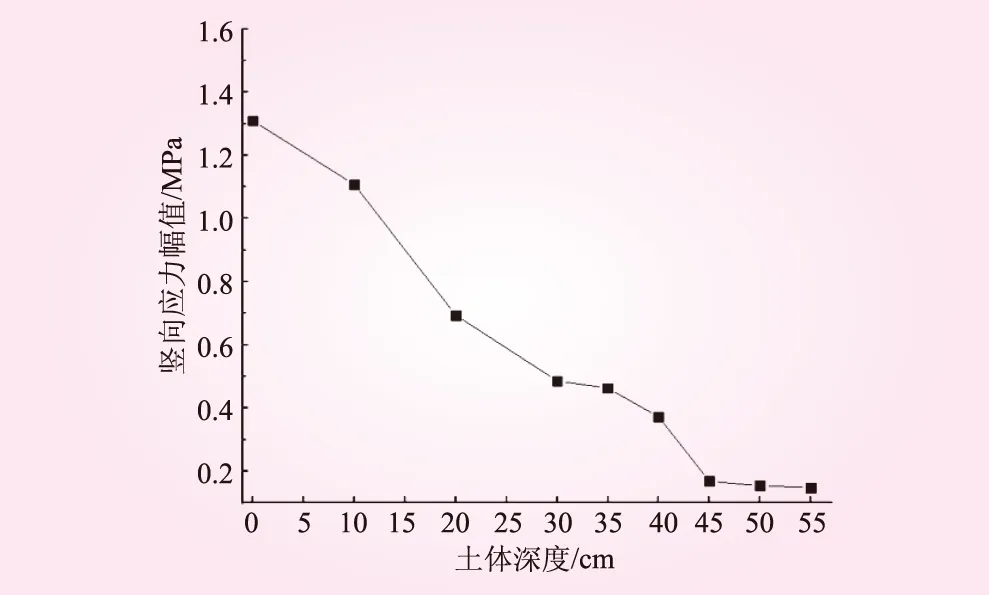
图9 竖向应力幅值随土体深度的变化曲线

由图8可知，竖向应力幅值与沉降量随碾压遍数的变化趋势是一致的，即激振力开始作用于砾石土时，砾石土表面产生的竖向应力幅值较小，随着碾压遍数的增加，表面竖向应力幅值也在不断增大，碾压7遍后，表面竖向应力幅值逐渐稳定在1.3 MPa左右。图9可以很直观地反映出竖向应力幅值随深度变化关系，其中0～30 cm为碾压层，30～55 cm为下垫层。当砾石土受到振动冲击作用时，土体表面的竖向应力幅值最大，土体深度从0～55 cm的竖向应力幅值都有不同程度的衰减，碾压层土体(0～30 cm)的竖向应力幅值沿着深度方向衰减幅度较大，而下垫层土体(30～55 cm)的竖向应力幅值沿着深度方向衰减幅度较小。

砾石土在受到激振力的振动作用时产生的压应力包括弹性反力和惯性力，土体的密实度越大，弹性反力也越大，即竖向应力幅值越大，故竖向应力幅值会随着碾压遍数的增加而增加，当达到一定的碾压遍数时，砾石土表面的竖向应力幅值逐渐趋于稳定。由于凸块碾产生的压实能量是沿着深度方向逐渐递减的，导致竖向应力幅值沿着深度方向逐渐递减，竖向应力幅值在下垫层的大小是比较明显的，这说明凸块碾的激振力对砾石土有较大的影响范围。

2.3 密度值分析

由于ABAQUS软件没有密度的量值输出，所以必须通过换算进行密度的求解与分析。在碾压过程中，碾轮与砾石土的作用时间很短，砾石土呈现弹性为主塑形为辅的特征[24]，由此可以得到冲压前后土体应变ε与密度ρ的关系为

(3)

式中，ρ0为土体的初始密度；ρ为冲压后的土体密度。

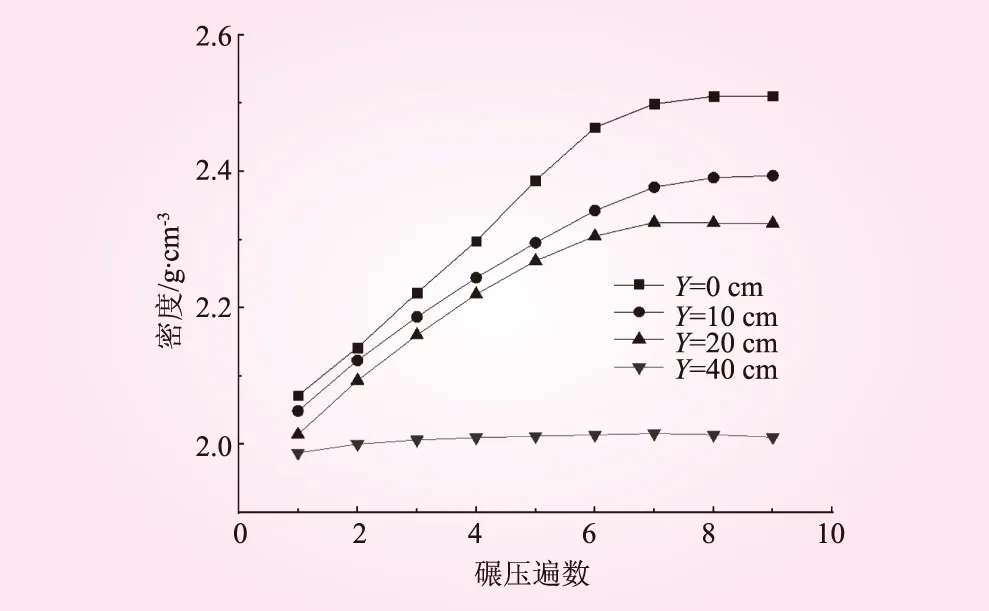
图10 不同深度的密度-遍数曲线

由图10可知，砾石土在一定深度(0～20 cm)下的密度值均随着碾压遍数的增加不断变大，当碾压7遍后，密度值的变化量均很小并逐渐趋于一个稳定值，此时砾石土表面(Y=0 cm左右)的密度值最大，约为2.50 g/cm3；密度值沿着深度方向逐渐递减，Y=10 cm和Y=20 cm处最终的密度稳定值分别为2.30、2.04 g/cm3，碾压层底部的密度值几乎为0。与此同时，深度0～20 cm范围内的土体均在碾压第7遍时密度值趋于一个稳定值，这说明此时凸块碾振动产生的压实能量能够有效传递到砾石土的一定深度，使砾石土在不同深度均能达到较好的压实效果。

2.4 竖向应力幅值分布特性分析

从碾轮的行驶方向以及宽度方向，分析竖向应力幅值的分布特性。图11是激振力作用在砾石土时，在压实轨迹中心上沿行驶方向均匀选取10个观测点的竖向应力幅值变化曲线。图12是激振力作用于某一区域时，沿轮宽方向选取11个观测点(观测点6在碾轮宽度方向的中心线上，观测点1～5和7～11对称分布于碾轮中心线两侧)的竖向应力幅值变化曲线。

图11 碾轮行驶方向的竖向应力幅值变化曲线

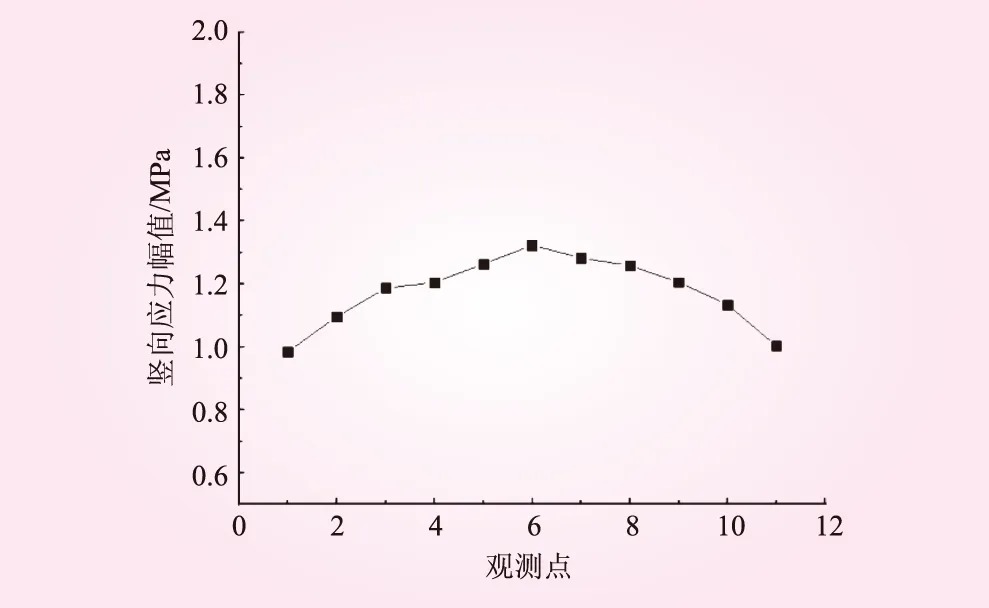
图12 碾轮轮宽方向的竖向应力幅值变化曲线

由图11可知，在激振力的作用下砾石土沿着凸块碾行驶方向的竖向应力幅值相差较小，振动压实时在长度方向保证压实效果的一致性和均匀性。由图12可知，凸块碾轮宽中心线上砾石土产生的竖向应力幅值最大，沿轮宽方向两侧的竖向应力幅值较小且呈近似为抛物线分布，这说明土体沿轮宽方向的压实均匀性不理想，即中间压实效果较好，而两边压实效果较差，从理论方向上解释了碾压作业中两两相邻的条带之间必须有一定的搭接宽度以保证每一个条带的压实质量。