基于CS 的大规模MIMO-OFDM 信道估计

王忆冉，朱留存，蒋昊天，刘 亮

（扬州大学，江苏 扬州225000）

传统的数字信号的调制是在单载波上进行的，这种调制方式易发生码间串扰,而且频谱利用率低，因此由于多径效应的影响而出现误码。OFDM 技术将信号进行串并转换，各路并行信号单独正交调制后再合为一路进行传输，无线信道划分为多个正交的子信道，就可以很好地克服上述缺点。MIMO 技术可以利用多天线信道和空时编码技术大幅度提高数据传输的速度，将系统信道容量线性提升。将两种技术结合，不仅可以发挥二者在传输上的优势，又可以克服码间串扰和信道间干扰，是5G 通信的关键技术。

在传统的MIMO-OFDM 系统信道估计算法中，导频的放置均需要满足奈奎斯特采样条件，这意味着系统必须传输大量的导频信号来对快速变化且具有强不确定性的信道参数进行采样，这些导频信号会占用大量的频带资源。压缩感知（CS）理论的问世为解决以上难题指明了方向。作为一种新的采样理论，CS 通过研究信号的稀疏性，仅仅需要对信号采集很少的测量值，便可通过重构算法恢复出原始信号。如果将压缩感知应用于信道估计中，代替奈奎斯特定理对信道参数进行采样，就可以在保证信道估计精确度的前提下，大幅减少所需传输导频的数量，为信息传输节省下更多的频带资源，图1 所示为MIMO-OFDM 整体框架图。

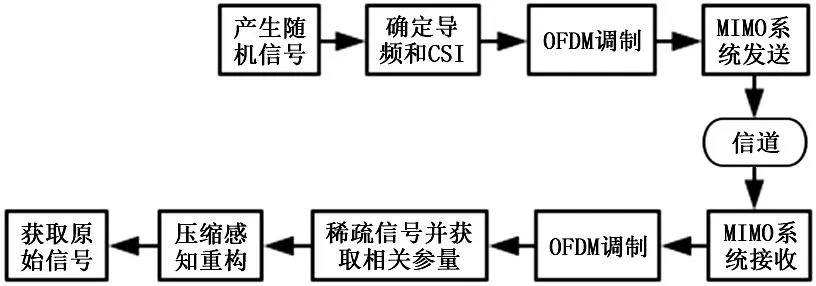
图1 MIMO-OFDM 整体框架图

现有的基于压缩感知稀疏信道估计技术可分为两类：①第一类算法是求解最小平方误差残差的非线性优化问题的近似方案，它是所有优势路径的增益和延迟位置的函数。这意味着在所有系数中联合进行优化。②第二类算法依次选择采样信道冲激响应的最重要抽头。目前，最通用的两种方法是凸优化算法之基追踪（BP）和贪婪算法之匹配追踪算法（MP）的变体OMP。BP 直接寻找使范数系数最小化的向量，这在计算上是昂贵的；OMP 通过选择在每次迭代中最大化改进表示的原子来迭代地建立稀疏信号。本文以OMP为研究对象，OMP 其核心算法是通过迭代找到残差最相关的列，进而通过求最小二乘解，得到信号稀疏表示系数估计最优值。但是，由于OMP 是通过迭代得到局部最优解，因此提出优化算法SCA，该算法能够对搜索空间，探索不同区域避免卡在局部最优解，进而收敛于全局最优解。正弦余弦算法是Seyedali Mirjalili 于2016 发表的算法，提出了一种新的基于种群的优化算法正弦余弦算法（Sine Cosine Algorithm，SCA）。其原理为首先创建多个初始随机候选解，并使用基于正弦和余弦函数的数学模型使这些解向外偏移或朝向最佳解。其核心公式为：

基于该算法的特点，将SCA 与OMP 结合在一起，主要优化的在于找到残差最相关的量，其优化步骤为：①初始化随机解X，定义区域为传感矩各列阵及残差内积；②根据优化目标函数，即OMP 重构算法中的传感矩阵A 各列与残差的内积绝对值，优化该函数来获得每个解的适应度，将最优的适应度的解作为当前目标P；③通过，来改变r1；并随机生成r2，r3，r4，r1指向内积绝对值优化下一个方向，r2定义移动距离，r3决定是否更新最优解，r4切换正弦余弦分量；④如果迭代次数满足设定的最大迭代次数，则结束迭代过程，否则转至步骤②，输出最优解。结果输出如图2 所示。可以清晰看到该优化算法能够精确重构信号，所用时间为0.692 513 s，较之OMP 重构算法减少了重构时长，针对于原始信号数量更大的相比较，其优化程度更明显。

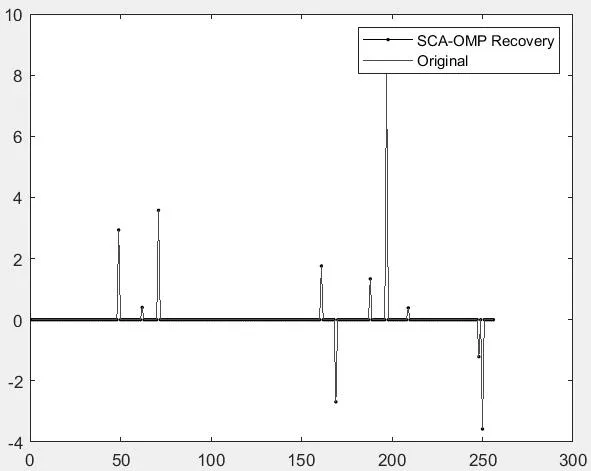
图2 SCA-OMP 重构信号对比图