一类基于同步多重休眠的损失制分组排队
2020-03-11毛学志刘思严
崔 瑜,毛学志,刘思严,牛 然
(河北科技师范学院数学与信息科技学院,河北 秦皇岛,066004)
损失制排队是一类经典的排队模型,其在发展过程中不断被丰富、优化,并被广泛应用于不同的实际问题。樊亦鸣[1]给出了带有柔性配置的损失制排队的平稳分布,并计算出顾客损失率,同时基于算法分析了相关参数对顾客损失率的影响。刘云杰[2]将损失制排队应用到多线程网络服务软件系统中,通过数据的采集,利用Maple软件进行编程计算出该系统的性能指标。李军等[3]基于损失制排队系统效率指标计算方法,建立了站点最优化车辆调配数(空桩数)的计算模型,并计算出苏州高新区金狮大厦站点在早晚高峰期应调配的车辆数。针对排队系统中的顾客流输入具有较大的差异性,张传龙[4]对顾客进行分类,将损失制与等待制排队模型进行组合,其仿真实验结果表明该策略提高了汽车检测的有效吞吐量,同时有效地降低了系统运行成本。黄健[5]以完善院内急救一体化制度,打通抢救流程的绿色通道为目的,设计了以损失制排队作为第一阶段的多阶段串联排队系统,并建立了以总滞留可能性最小为目标的数学规划模型,对各科室床位进行优化配置,其结果对多阶段床位资源的配置优化具有重要意义。以上文献对经典的损失制排队进行了发展,却较少涉及节约系统能耗的研究。
针对排队系统产生的能耗浪费问题,部分文献引入休假排队理论。
为了在移动宽带城域网中获得更好的节能效果,张丽媛等[6]建立了带有休假延迟且休假长度指数变化的多重休假排队模型,并给出了系统切换率、能量节省率和平均响应时间等性能指标的解析表达式。曹建[7]针对区块链技术提出了一种新的节能运行机制,将比特币故障矿池运行模式建模为带休眠唤醒策略和工作故障策略的排队系统,并通过构造能耗函数和节能率函数分析矿池能耗。马占友等[8]以提高云系统的节能水平为目标,同时兼顾虚拟机状态频繁切换所造成的损失,将同步休眠和异步休眠相结合,提出一种基于M/M/c休假排队理论的虚拟机调度策略。李君[9]使用空竭服务的休假排队模型对异构云计算中的任务调度进行建模,并提出一种任务调度算法,以降低云计算的系统能耗。徐刚[10]利用母函数方法,求出了带有中途退出的M/M/1单重工作休假排队系统忙期和工作休假期的相关性能指标,并给出两个服务率对系统性能指标影响的数值结果分析。
受以上文献启发,有别于现有研究成果,笔者围绕系统能耗节约问题对经典的损失制排队进行了优化和改进。以保证系统响应性能与节约系统能耗为目标,本次研究建立了一个基于同步多重休眠机制,带有双速率可调节的M/M/m+n/m+n损失制分组排队。通过构造马尔科夫链和利用矩阵几何解得出两个系统性能指标:顾客的平均逗留时间和系统节能率。基于Matlab软件通过数值实验笔者还给出了休眠机制对两个系统性能指标的影响分析。
1 模型描述
为缓解损失制系统产生的能耗浪费问题,实现绿色节能,本次研究将损失制系统中的所有服务台分为两组,并引入同步多重休眠机制[11]。顾客进入系统的流程见图1。
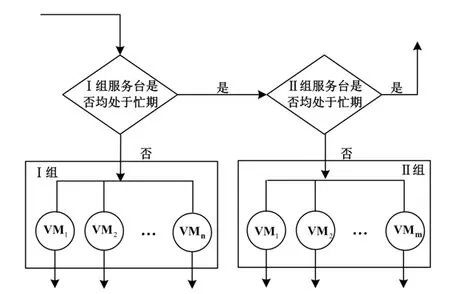
图1 损失制排队系统流程
假定顾客到达为参数λ(λ>0)的泊松流,若Ⅰ组有空闲的服务台可提供服务,则顾客立即进入Ⅰ组接受服务。假设Ⅰ组有n个同构的服务台,设L为调节服务台服务速率的阈值,当Ⅰ组处于忙期的服务台数量不足L时,每个正在接受服务的顾客所需服务时间均服从参数为μ0的负指数分布;而当处于忙期的服务台数量达到L时,每个正在接受服务的顾客所需的服务时间均服从参数为μ1(μ1>μ0)的负指数分布。顾客接受完服务后立即离开系统。
当顾客到达系统时,若Ⅰ组所有服务台均处于忙期,则顾客到达Ⅱ组。若Ⅱ组所有服务台也均处于忙期,则顾客不会等待,立即离开系统。
当顾客到达Ⅱ组时,Ⅱ组至少有一个空闲的服务台可提供服务,则顾客立即进入Ⅱ组接受服务。假设Ⅱ组有m个同构的服务台,每个正在接受服务的顾客所需服务时间服从参数为μ2的负指数分布。当Ⅱ组所有顾客接受完服务离开系统后,Ⅱ组所有服务台将同步进入休眠状态。
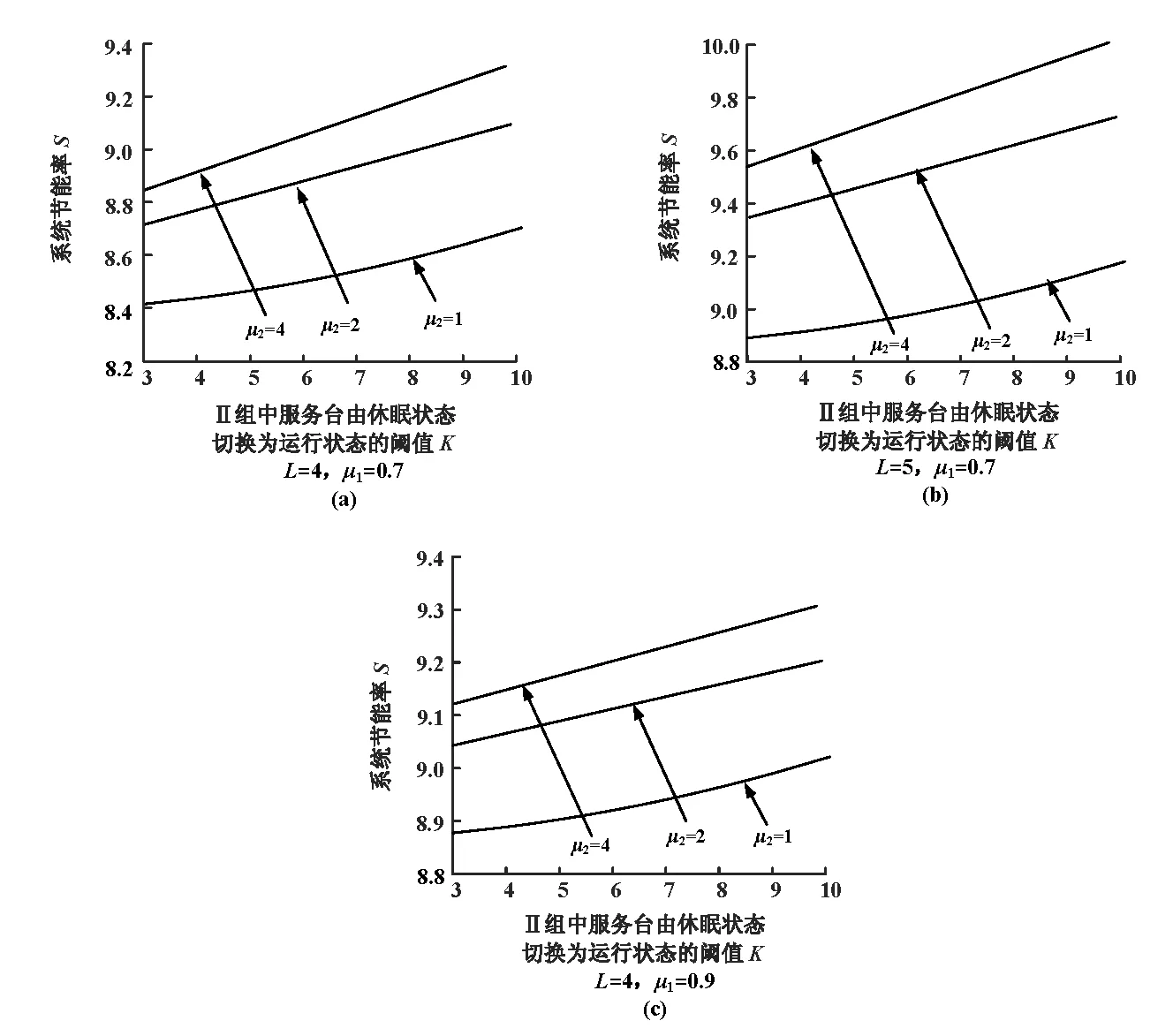
当顾客到达Ⅱ组时,Ⅱ组服务台正处于休眠状态,则顾客进入Ⅱ组服务台处等候。当等候的顾客数达到阈值K(0 当Ⅱ组服务台处于忙期时,一旦Ⅰ组出现空闲服务台且无新到达顾客,倘若系统中总的顾客数大于0且小于阈值L,则Ⅱ组中的顾客将全部被迁移到Ⅰ组接受服务,且服务率为μ0,同时Ⅱ组服务台随即进入同步休眠状态;倘若系统中总的顾客数大于等于阈值L且小于等于n,则Ⅱ组中的顾客全部被迁移到Ⅰ组接受服务,但服务率为μ1。 此外,约定到达时间间隔、服务时间是相互独立的,排队规则为先到先服务[12]。基于以上假设,得到一个M/M/m+n/m+n损失制分组排队。 设随机变量S1(t)表示t(t≥0)时刻Ⅰ组服务台所处的状态,其中S1(t)=0与S1(t)=1分别表示低速和高速状态,随机变量S2(t)表示t时刻Ⅱ组服务台所处的状态,其中S2(t)=0与S2(t)=1分别表示运行状态与休眠状态。设随机变量N1(t)=i(i∈{0,1,…,n})表示t时刻Ⅰ组的顾客数量,随机变量N2(t)=j(j∈{0,1,…,m})表示t时刻Ⅱ组的顾客数量。那么,{(S1(t),N1(t),S2(t),N2(t)),t≥0}是一个拟生灭过程(QBD)[13],设QBD的状态空间为Ω,且 Ω=Ω0∪Ω1∪…∪Ωm 其中, Ω0={(0,0;0,0),(0,1;0,0),…,(0,L-1;0,0),(1,L;0,0),…,(1,n;0,0)} Ω1={(1,n;0,1),(1,n;1,1)} ⋮ ⋮ ΩK-1={(1,n;0,K-1),(1,n;1,K-1),…,(1,n-K+2;1,K-1)} ΩK={(1,n;1,K),(1,n-1;1,K),…,(1,n-K+1;1,K)} ⋮ ⋮ Ωm={(1,n;1,m),(1,n-1;1,m),…,(1,n-m+1;1,m)} 设QBD的生成元[13]为矩阵Q,且 (1) 其中,A0为一个(n+1)(n+1)阶方阵,且 Au(u=1,2,…,K-1)为一个(u+1)×(u+1)阶方阵,且 而Au(u=K,K+1,…,m-1)为一个u×u阶方阵,且 Au= Am为一个m×m阶方阵,且 Am= B1为一个2×(n+1)阶矩阵,且 Bu(u=2,3,…,K-1)为一个(u+1)×u阶矩阵,且 Bk为一个K×K阶矩阵,且 Bu(u=K+1,K+2,…,m)为一个u×(u-1)阶矩阵,且 C0为一个(n+1)×2阶矩阵,且 Cu(u=1,2,…,K-2)为一个(u+1)×(u+2)阶矩阵,且 CK-1为一个K×K阶矩阵,且 Cu(u=K,K+1,…,m-1)为一个u×(u+1)阶矩阵,且 设{(S1(t),N1(t),S2(t),N2(t)),t≥0}在任一状态下的稳态概率为πk,i;l,j,且 设{(S1(t),N1(t),S2(t),N2(t)),t≥0}水平为j的稳态概率向量为πj,j=0,1,…,m,且 π0=(π0,0;0,0,π0,1;0,0,…,π0,L-1;0,0,π1,L;0,0,…,π1,n;0,0) ⋮ ⋮ πK-1=(π1,n;0,K-1,π1,n;1,K-1,…,π1,n-K+2;1,K-1) πK=(π1,n;1,K,π1,n-1;1,K,…,π1,n-K+1;1,K⋮ ⋮πm=(π1,n;1,m,π1,n-1;1,m,…,π1,n-m+1;1,m 设{(S1(t),N1(t),S2(t),N2(t)),t≥0}的稳态概率分布为Π,则 Π=(π0,π1,…,πm) 结合连续时间马尔科夫链的稳态平衡方程以及归一化条件,稳态概率分布Π与矩阵Q满足方程组如下: (2) 设Ⅰ组中顾客的平均逗留时间为E[W1],且 (3) 设Ⅱ组中顾客的平均队长为E[N],且 设Ⅱ组中顾客的平均逗留时间为E[W2],由Little公式[12]可得 设整个系统中顾客的平均逗留时间为E[W],则 E[W]=E[W1]+E[W2] (5) 设Ⅰ组服务台由高速状态转换为低速状态后单位时间内所节省的能量为S1,且 (6) 其中,H1和H2分别表示单位时间内Ⅰ组服务台处于高速状态和低速状态所消耗的能量。 设Ⅱ组服务台由运行状态转换为休眠状态后单位时间内所节省的能量为S2,且 (7) 其中,H3和H4分别表示单位时间内Ⅱ组服务台处于运行状态和休眠状态所消耗的能量。 设Ⅱ组服务台单位时间内被唤醒过程中所消耗的额外总能量为S3,且 S3=H5π1,n;0,K-1λ (8) 其中,H5表示Ⅱ组服务台单位时间内每次休眠结束被唤醒所消耗的能量。 设单位时间内整个系统节省的能量即系统节能率为S,则 S=S1+S2-S3 (9) 为分析所提出的休眠机制对两个性能指标的影响,笔者在MATLAB R2016a环境下进行数值实验,并给出结果分析。数值实验中系统参数假设见表1。 表1 数值实验参数 实验结果表明,顾客的平均逗留时间E[W]会随着Ⅱ组休眠阈值K的增大呈现上升趋势(图2(a),图2(b),图2(c))。因为当Ⅱ组服务台处于休眠状态时,新到达的顾客需要在服务台等待,休眠阈值K越大,顾客需要等待的时间就越长,从而系统中顾客的平均逗留时间E[W]就越大。而对于相同的休眠阈值K,E[W]会随着Ⅱ组服务台的服务率μ2的增大而减少。因为μ2越大,Ⅱ组服务台服务速率越快,从而系统的整体服务效率越高,所以系统中顾客的平均逗留时间E[W]就越小。 当Ⅰ组服务台的服务率μ1=0.7,Ⅱ组休眠阈值K=3,Ⅱ组服务台的服务率μ2=1时,顾客的平均逗留时间E[W]与Ⅰ组阈值L的关系见图2(a)与图2(b),E[W]会随着的增大而增加。因为L越大,Ⅰ组服务台低速运行的时间就越长,从而系统整体服务时间就越长,那么顾客的平均逗留时间E[W]就越大。 当Ⅰ组阈值L=4,Ⅱ组休眠阈值K=3,Ⅱ组服务台的服务率μ2=1时,顾客的平均逗留时间E[W]与Ⅰ组服务台的服务率μ1的关系见图2(a)与图2(c),E[W]会随着μ1的增加而减少。因为μ1越大,Ⅰ组服务台的服务速率越快,从而系统的整体服务效率越高,相应地,顾客的平均逗留时间E[W]就越小。 实验结果亦表明,系统节能率S会随着Ⅱ组休眠阈值K的增大呈现上升趋势(图3(a),图3(b),图3(c))。因为K越大,Ⅱ组服务台处于休眠状态的时间就越长,从而整个系统的能量消耗会降低,即系统节能率S会增大。而对于相同的休眠阈值K,S会随着Ⅱ组服务台的服务率μ2的增大而增加。因为μ2越大,Ⅱ组服务台的服务速率越快,从而该组服务台为所有顾客服务完进入休眠状态的概率就越大,相应地,系统节能率S会随之增加。 图2 顾客平均逗留时间的变化趋势 图3 系统节能率的变化趋势 当Ⅰ组服务台的服务率μ1=0.7,Ⅱ组休眠阈值K=3,Ⅱ组服务台的服务率μ2=4时,系统节能率S与Ⅰ组阈值L的关系见图3(a)与图3(b),S会随着L的增大而增加。因为L越大,Ⅰ组服务台低速运行的概率就越大,从而系统的能量消耗就比较少,所以系统节能率S会增加。 当Ⅰ组阈值L=4,Ⅱ组休眠阈值K=3,Ⅱ组服务台的服务率μ2=4时,系统节能率S与Ⅰ组服务台的服务率μ1的关系见图3(a)与图3(c),S会随着μ1的增大而增加。因为μ1越大,Ⅰ组服务台的服务速率越快,即能够使顾客尽快接受完服务离开系统,从而Ⅰ组服务台由高速运行状态转为低速运行状态的概率就越大,进而降低能量消耗,所以系统节能率S增加。 为了保障排队系统响应性能的同时尽可能减少系统能耗,缓解资源浪费问题,笔者将系统所有服务台分为两组,其中一组引入双速率可调节机制,另外一组引入同步休眠机制。为了进一步节省系统能耗,本次研究还设置了两组之间的任务可迁移策略。基于以上方案,笔者建立了一个M/M/m+n/m+n损失制混合分组排队。通过构造四维马尔科夫链,利用矩阵几何解方法推出系统的稳态概率分布,进而得到顾客平均逗留时间和系统节能率两个性能指标。最后通过数值实验给出两个指标的性能分析。 本次研究针对损失制排队系统的节能问题提出一个优化方案。后续的研究重点则是基于算法对休眠阈值进行数值优化,同时考虑从经济学角度出发,引入博弈思想,构造收益函数,提高系统的经济效益。2 模型的稳态概率分布
π1=(π1,n;0,1,π1,n;1,1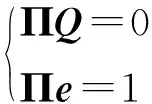
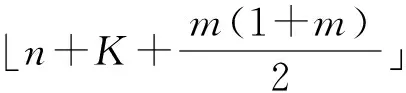
3 系统的性能指标
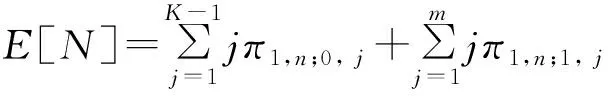

4 数值结果


5 结论与讨论
