地铁地下车站结构的地震反应分析
2020-03-10刘喆
刘喆
(南昌轨道交通集团有限公司南昌330038)
0 引言
随着城市现代化进程的不断加快,各大城市通过修建地铁带动城市更新和升级,使得市民出行更加高效快捷,交通拥堵状况得到缓解,地铁建设和运营里程数逐年增加。地铁与城市高度融合发展,已成为重要的城市生命线工程,在地震活跃地区一旦遭遇强震作用发生整体坍塌,将会带来难以估量的经济损失和人员伤亡。地铁结构震害修复施工难度大、成本高、工期长,对震后城市功能正常运行带来不利影响。提高地下地铁结构的抗震能力,保证结构在地震中的完整性,对于保障乘客的生命财产安全和降低震害修复成本具有重要意义。因此,对地下地铁结构的地震破坏模式和抗震机理进行深入研究很有必要。
传统理论认为地下结构由于受到围岩土体的约束而具有较强的抗震能力,在遭遇地震作用时破坏程度较轻,但是自从日本大开地铁车站在阪神地震中出现严重震害,车站结构中柱发生大范围坍塌,从而改变了人们的观念,地下地铁结构的抗震问题得到各国学者的普遍关注,逐渐成为工程结构抗震领域研究的焦点。宋磊等人[1]分别采用惯性力法和反应位移法计算了软土地区地铁车站结构的地震反应内力,并进行了比较分析。林利民等人[2]构建了在软土浅埋条件下土体与地下车站结构的动力相互作用模型,通过改变车站埋深、土层分布状况和结构类型等参数,研究不同条件下地铁车站结构的地震响应,并分析得到影响车站抗震性能的主要因素。路德春等人[3]研究了双层地下车站结构与围岩土体系统在斜入射地震作用下的三维地震反应,对地铁车站结构地震响应的空间效应和变形规律进行了深入分析。还毅等人[4]提出了柔性动边界梁在轴力和地震荷载组合作用下动力响应的理论模型,通过改变轴力、弹簧刚度和阻尼系数等计算参数,对比分析了不同条件下结构的动力响应,并利用有限元软件对地铁车站在有无设置隔振器的情况下的地震响应,进行了三维非线性动力分析。庄海洋等人[5]考虑了土与混凝土的材料非线性特性以及土与混凝土结构的界面接触非线性特性,采用数值方法计算了地下车站结构的地震反应,得到了结构层间相对位移和结构构件连接处节点应力的反应规律,以及各结构构件的动态损伤演化规律。王国波等人[6]研究了软土地区地铁车站结构的地震响应规律,通过建立三维有限元模型分析了地震荷载作用下结构的内力增幅和结构的抗震薄弱部位。杜修力等人[7]通过建立在日本阪神地震中损毁的大开地铁车站的三维有限元数值分析模型,从结构构件不同的受力性能、围岩土体分布状况对车站结构地震反应的影响、结构体系受力分布变化引起的中柱、侧墙变形能力不协调等几个方面,对大开地铁车站的地震破坏机理进行了系统分析。赵伯明等人[8]采用瑞利阻尼和基于Hardin/Drnevich 模型的滞后阻尼,模拟土在循环动荷载下的滞回特性,建立三维有限元数值计算模型,对软土地区某双层三跨地铁车站结构进行地震反应分析,研究了地下车站结构与土体相互作用机制及主要结构构件的受力性质。
本文首先建立地下车站结构的平面有限元模型,由土层一维自由场分析得到各土层相对于结构底部的相对位移、自由土层加速度和结构周围剪力,采用反应位移法计算结构在适合本工程场地的地震作用下的内力响应。对比平面有限元计算结果,采用专业岩土工程有限元计算软件MIDAS GTS NX 建立地下地铁车站结构的空间三维有限元数值分析模型,以场地环境相近的 El Centro 波、TAR-TARZANA 波和兰州波作为初始时程,人工合成适合本工程场地的地震动加速度时程,以此作为输入地震荷载对结构进行地震响应时程分析,得到车站结构内力和侧移的变化规律,以及结构整体的抗震性能,提出相应的抗震设计措施。
1 工程概况
采取某地铁地下3 层岛式车站作为研究对象,该车站主体结构自下而上由站台层、设备层和站厅层组成,结构型式采用现浇钢筋混凝土箱形结构。车站结构总长度为143.9 m,主体结构标准段宽度为21.9 m,底板埋深为22.96 m,主体结构端头井处宽度为25.6 m,底板埋深为23.04 m 。本工程建设场地地下水位埋深为4.6~6.6 m,计算模型中地下水位取到水平地面。本工程场地抗震设防烈度为6 度,50 年超越概率10%的基岩地震动峰值加速度为0.093 g。场地类别为Ⅱ类,设计地震分组为第一组。
车站主体结构标准段横截面主要结构构件尺寸及结构地震响应测点布置如图1所示,侧墙、各层楼板及纵梁采用C35 混凝土,中柱采用C45 混凝土。各层楼板与侧墙相交位置、中柱与各层楼板连接节点处、各层楼板跨中附近均为内力较大部位,在强震作用下可能出现较大的地震响应,为了观测结构内力分布状态的变化规律及安全性,故在这些结构关键位置布置测点,时程计算结果用于抗震分析。
该车站工程建设场地位于赣江冲积平原区,按场地地层岩性及其工程特性,地层自上而下依次划分为〈1-2〉素填土、〈2-1〉粉质粘土、〈2-2〉淤泥质粉质黏土、〈2-3〉细砂等,各土层的物理力学参数取值如表1所示。
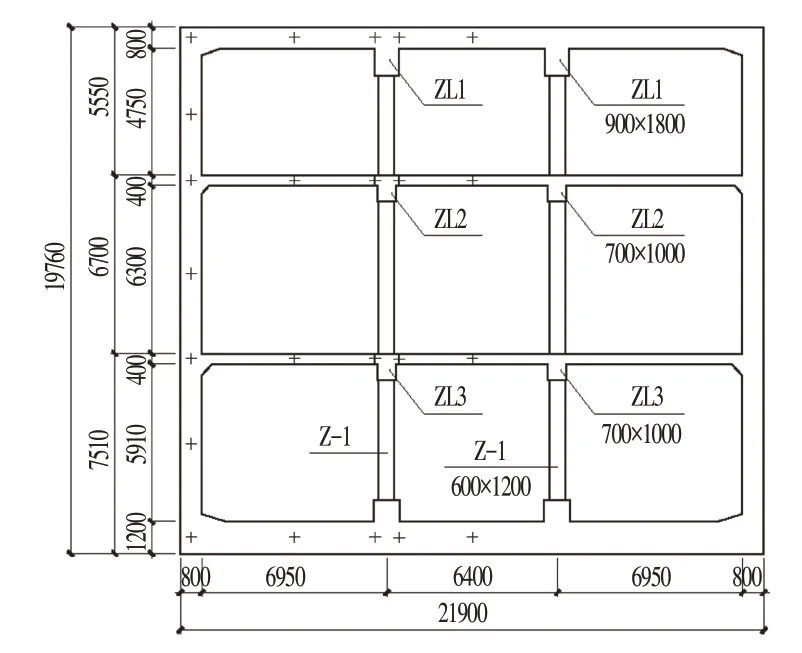
图1 车站主体结构标准截面及地震响应测点布置Fig.1 Standard Section of Main Structure of Station and Layout of Seismic Response Measuring Points
2 基于静力法的抗震分析
在进行车站结构计算时通常要考虑地震荷载组合,地震作用下结构内力和位移计算通常采用静力法,静力法是一种力学概念明晰的简化计算方法,实际工程计算中常用的静力法有反应位移法和反应加速度法等,反应加速度法是将结构所在位置相应的水平加速度施加在结构上计算内力和变形,本文采用反应位移法计算结构的地震作用效应。在得到关键截面控制内力之前首先计算结构在自重、水土压力等静力荷载作用下的内力分布,接下来通过反应位移法获得地震荷载作用下的内力分布。
2.1 静力计算模型
地震荷载组合是在地下车站结构计算分析时需要考虑的荷载组合之一,由永久荷载作用效应和地震荷载作用效应组合得到。本文通过有限元分析程序建立平面有限元模型,计算车站结构在永久荷载作用下的内力,结构各组成构件采用梁单元,假定地下连续墙和主体结构采用两端铰接的受压刚性链杆连接,侧向水压力施加在主体结构的侧墙上,侧向土压力施加在地下连续墙上,用仅受压的土弹簧模拟地基土对结构的支撑作用,车站结构埋深3 m,地下水位取到水平地面。梁单元采用beam3 单元,受压刚性链杆采用link10 单元,地基弹簧采用combin14 单元。计算模型材料容重按荷载规范取值如下:混凝土25 kN/m3,围岩土体 20 kN/m3,装修材料22 kN/m3,地下水10 kN/m3。
结构自重由计算机程序自动计算,车站顶板上覆水土压力为20 kPa,地下1层装修及管线荷载为5.3 kPa,地下2层装修、管线及设备荷载为12.2 kPa,底板水压力为227.6 kPa。结构在使用阶段的侧向水土压力按静止土压力计算,施加在地下连续墙上、下两端的侧向土压力分别为28.9 kPa、188.4 kPa,施加在主体结构侧墙上、下两端的侧向水压力分别为34 kPa、221.6 kPa。车站结构静力计算模型及其荷载作用如图2所示。

图2 车站结构静力计算模型及荷载Fig.2 Calculation Model and Load Diagram of Station Structure
2.2 反应位移法计算模型
反应位移法是一种将围岩土体在地震荷载作用下的相对位移、结构与周围土层之间的剪力以及结构自身惯性力作为静荷载作用在结构上,从而计算地下结构地震响应的静力计算方法。反应位移法计算模型中主要的地震作用力,是场地土层在地震作用下的变形,惯性力对结构的作用效应相对较小。结构采用梁单元建立平面有限元计算模型,假定结构周围土层为匀质弹性体,利用地基弹簧模拟围岩土体对结构的支撑作用。采用压缩弹簧和剪切弹簧分别表示土体对结构表面的正向和切向作用,采用地基弹簧刚度定量表示土体与结构之间的相互作用,通过地基水平或垂直基床系数乘以土体对结构表面的作用面积计算地基弹簧刚度。车站结构反应位移法计算模型及其荷载作用如图3所示。
地基弹簧刚度 kv、ksv、kh、ksh通过下列公式计算:
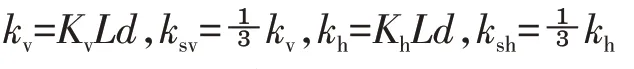
式中:Kh为地基水平基床系数;Kv为地基竖向基床系数;L 为结构横向垂直方向的计算长度;d 为土层沿车站结构纵向的计算长度。
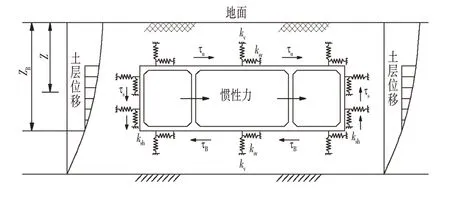
图3 反应位移法计算模型Fig.3 Calculation Model of Reaction Displacement Method
在用反应位移法对地下车站结构进行抗震计算时,首先通过一维自由场土层地震反应分析确定地下车站结构顶底板发生最大相对位移时,各土层相对于结构底板的位移,将各层相对位移作为静荷载通过周围的地基弹簧,作用在相应位置的结构单元上。结构惯性力可由地下车站结构顶底板发生最大相对位移时,各结构单元的最大加速度乘以单元质量计算,并将水平惯性力作用在相应的结构单元上。由一维自由场土层地震反应分析得到的结构顶底板位置处的自由土层剪力,确定地下车站结构顶底板与围岩土体之间的剪力,结构侧壁剪力取为顶底板剪力的平均值。
2.3 内力分析结果
将永久荷载施加在结构平面有限元计算模型上得到静力作用下的内力分布,利用MIDAS 一维自由场分析得到各土层的相对位移、加速度反应和剪应力,将这些荷载施加在车站结构平面有限元模型上,计算得到地震反应内力分布。在分别计算得到静力荷载和地震荷载作用下的车站结构内力分布后,进行荷载组合时永久荷载内力分项系数取1.2、地震反应内力分项系数取1.3,由于车站结构的内力计算截面和计算分析考虑的荷载组合工况较多,无法逐一列举,这里仅列出车站结构标准断面的考虑地震荷载组合工况的计算内力,如图4所示。
由以上考虑地震荷载的偶然组合作用下的内力分析结果可以看出:①在车站结构正常使用阶段,抗震工况计算在关键构件设计中对结构内力不起控制作用;②在地震荷载作用下,侧墙与各层楼板相交处,车站结构顶底板与侧墙、中柱连接部位的弯矩和剪力较大,结构顶底板各跨跨中位置也有较大弯矩,中柱弯矩、剪力较小,最大轴向压力出现在结构中柱与底板连接节点处,各层楼板轴力也较大。
3 基于时程分析法的抗震分析
3.1 三维有限元模型
用于抗震时程分析的三维有限元数值计算模型采用大型岩土工程有限元软件MIDAS GTS NX建立,由于整个车站的有限元模型单元数量庞大,考虑到计算机的运算速度和储存有限,故只截取车站标准段的一部分计算,车站周边围岩土体采用三维实体单元模拟,土体本构关系采用各向同性Mohr-Coulomb模型模拟,物理力学参数按表1取值,车站中柱模拟采用二维梁结构单元,车站侧墙及各层楼板模拟采用平面板结构单元,本构关系均为线弹性模型,C45混凝土弹性模量为3.35×104MPa,C35 混凝土弹性模量为 3.15×104MPa。构建粘弹性人工边界模拟模型边界条件,该边界条件常用于地下结构-土体相互作用非线性动力分析,既可以保证地震散射波从截取的有限范围计算模型中穿过人工边界时不会产生反射,也可以精确模拟模型人工边界以外的半无限空间弹性体的弹性恢复性能,保证计算结果具有较高的准确性。模型四周人工边界与车站结构的距离取3 倍结构水平宽度,底部人工边界取至地震作用基岩面,与结构底板的距离取3 倍结构竖向高度。车站结构的三维有限元数值计算模型及平面框架有限元模型如图5、图6所示。
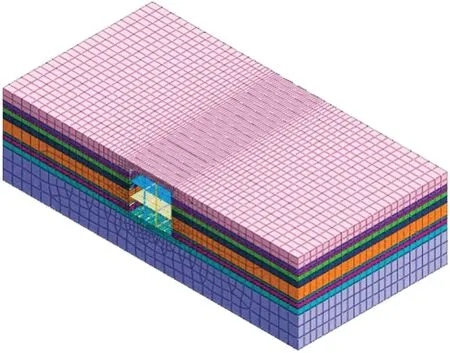
图5 车站结构三维有限元模型Fig.5 Three Dimensional Finite Eement Model of Station Structure
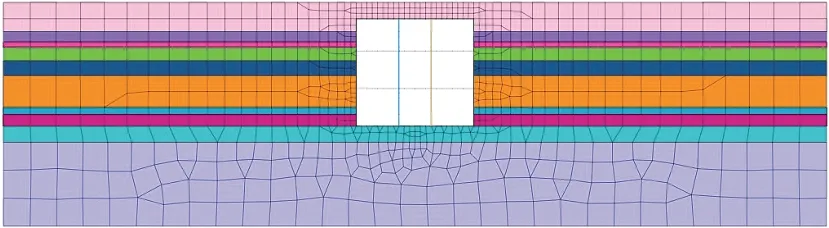
图6 车站结构平面框架有限元模型Fig.6 Finite Element Model of Plane Frame of Station Structure
3.2 地震波输入
为了保证时程分析和抗震设计更贴近实际,地震动三要素(包括频谱特性、地震动加速度峰值、地震动持时)在模型输入地震波时需要考虑。输入模型的地震动加速度时程应能真实地反映实际发生地震动的频谱特性和相位特性,保证车站结构地震反应分析的准确性和合理性。根据《城市轨道交通结构抗震设计规范》的建议,使用与本工程场地环境相近的实际强震动加速度时程作为初始时程人工合成抗震分析所需的地震动时程,人工合成的地震动加速度反应谱曲线与设计地震动加速度反应谱曲线的误差应小于5%[9]。加速度时程曲线峰值取50 年超越概率10%的地震动加速度峰值,根据《地震安全性评价报告》为93 cm/s2。地震动持时应当包含地震加速度时程中最大部分,通常取结构基本周期的5~10倍,本文取20 s。
根据《建筑抗震设计规范:GB50011-2010》[10],本地区抗震设防烈度为6度,按罕遇地震考虑,水平地震影响系数最大值αmax=0.28,Ⅱ类场地,设计地震分组为第一组,场地特征周期为0.35 s,阻尼比取0.05,本工程设计地震动加速度反应谱曲线如图7所示。本文选择适用于Ⅱ类场地的El Centro 波、TAR-TARZANA 波和兰州波作为初始时程,根据设计地震动加速度反应谱曲线人工合成抗震分析所需的地震动加速度时程曲线如图8所示。
图7 罕遇地震设计地震动加速度反应谱曲线Fig.7 Acceleration Response Spectrum Curve of Rare Earthquake
图8 加速度时程曲线Fig.8 Acceleration Time History Curve
3.3 车站地震响应计算结果分析
3.3.1 层间位移分析
在水平向地震荷载作用下,地下车站结构会随周围土体一同发生侧向变形,一旦侧移超过限值,结构会丧失整体承载能力,抗侧向变形能力是结构抗震分析的重点。分别提取El Centro 波、TAR-TARZANA 波和兰州波激励下,车站结构中柱与各层楼板相交节点在各时刻的侧向位移,通过计算分析得到各楼层层间相对位移的最大值及层间位移角如表2所示。
由表2 可以看出,中间层的最大层间相对位移比其它两层要大,这是因为中间层受周围土层的约束作用较小。同一种地震波激励下,车站结构右摆和左摆的层间相对位移基本相同,左摆层间相对位移略大一些。在兰州波作用下,结构中间层右摆的层间相对位移最大,最大值为10.6 mm,相应的最大层间位移角为1/660。该车站结构的抗震性能要求为Ⅱ级,按罕遇地震计算,《城市轨道交通结构抗震设计规范》规定层间位移角限值为1/250,结构最大层间位移角在限值范围内,结构抗侧向变形能力良好。
从图9a可以看出,地下车站结构在El Centro地震波激励下,站厅层、设备层和站台层的最大层间相对位移分别为6.67 mm、9.67 mm、5.70 mm,各层层间相对位移均在时刻2.24 s 出现峰值,各楼层侧向变形同时达到最大。由图9b 可以得出,沿X 轴方向(结构横向)输入El Centro 地震波荷载,自上而下各楼层的最大层间位移角分别为 1.11×10-3、1.38×10-3、8.14×10-4,各层层间位移角出现峰值的时刻均为2.24 s,与各层最大层间相对位移达到峰值的时刻一致,处于规范要求的限值范围内,结构抗侧向变形能力良好。

表2 车站结构最大层间相对位移和层间位移角Tab.2 Maximum Relative Displacement between Layers and Displacement Angle between Layers of Station Structure
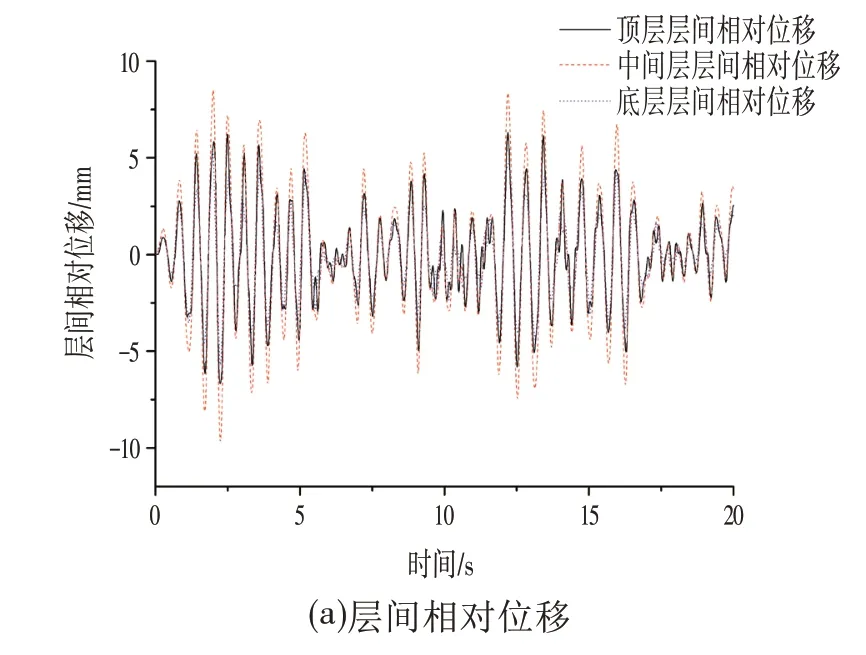

图9 El Centro波时程曲线Fig.9 Time History Curve of El Centro Wave
3.3.2 结构内力分析
通过在车站结构模型基岩面输入沿x 轴方向(横向)的3种地震波荷载,得到车站结构关键部位的内力响应幅值,由于3 种地震波激励荷载施加在计算模型上的结构内力反应规律基本一致,这里仅列出输入El Centro 地震波时的结构主要构件内力,如表3所示。
从表3 中可以看出,结构最大内力响应均出现在结构各主要构件的连接部位。首先分析弯矩,中柱的弯矩幅值出现在中柱与结构顶板连接节点处,最大值为2 048.01 kN·m,中柱与结构底板连接节点处也出现较大弯矩,弯矩值为1 223.09 kN·m。侧墙的弯矩幅值出现在侧墙与结构顶、底板相交位置,上侧墙与顶板连接区域的弯矩幅值为374.08 kN·m,下侧墙与底板连接区域的弯矩幅值为494.37 kN·m,中间层侧墙与中板连接处弯矩幅值大于顶、底层侧墙与中板连接处弯矩幅值,各层侧墙中部出现了较大弯矩。顶板、中间层楼板、底板的最大弯矩幅值出现在板与侧墙相交位置,其中最大弯矩为顶板与侧墙相交处的弯矩为421.11 kN·m,各层楼板与中柱相交处弯矩次之。顶、底板边跨跨中位置出现了较大弯矩,其次是各层楼板中跨跨中弯矩,中间层楼板边跨跨中弯矩相对较小,顶板和底板的弯矩幅值要大于中间层楼板的弯矩幅值。
对于剪力,顶层中柱剪力明显大于以下两层中柱剪力,这是由于顶层柱侧移刚度较小造成,且自上而下逐层减小,各层柱下端剪力大于上端剪力。顶层中柱与地下一层楼板连接节点处的剪力幅值最大,中柱剪力最大值为524.66 kN。侧墙各部位的剪力幅值在侧墙与底板相交区域达到最大,侧墙最大剪力值为214.55 kN,顶层侧墙与顶板连接处、中间层侧墙与地下一层楼板连接处剪力较大,分别为165.17 kN 和108.97 kN,顶层侧墙与中间层侧墙的剪力自上而下逐渐递减,而底层侧墙的剪力自下而上逐渐递减。底板与侧墙连接部位剪力幅值最大,最大值为431.42 kN,顶板与侧墙相交处、顶板与中柱相交处出现了较大剪力,中间层楼板剪力分布较为平均。
对于轴力,中柱轴力自上而下逐渐增大,在中柱与底板相交节点处出现最大轴力幅值,中柱轴力最大值为523.98 kN。侧墙轴力变化呈现自上而下逐渐增大趋势,底层侧墙与底板相交端部截面轴力幅值达到最大,侧墙最大轴力值为799.04 kN。各层楼板与侧墙连接位置处轴力不能忽略,顶板、底板各控制截面轴力大于中间层楼板相应位置轴力,顶、底板与侧墙连接处截面的水平轴力幅值分别为231.77 kN、366.52 kN,各层楼板与中柱连接节点处也存在较大轴力。
由上述分析可知,地下车站结构中柱与顶底板连接部位、侧墙与顶底板相交处、结构顶底板与侧墙相交位置附近、各层楼板与中柱连接节点处、顶底板边跨跨中的内力响应幅值均出现了较大值,这些位置均为抗震薄弱环节,需要加强抗震措施。尤其对于结构中柱,柱上下两端与顶、底板连接节点处弯矩特别大,容易发生弯曲破坏,这些部位率先在结构中形成塑性铰,同时中柱还承受顶板自重、作用在顶板上的较大水、土压力和地面车辆荷载,中柱两端混凝土达到极限压应力压碎,从而出现严重的压弯破坏,最终导致结构整体垮塌,因此特别需要加强中柱上下两端截面的抗震设计。
由图10可以看出,将El Centro 地震波沿X轴方向施加在车站结构上,中柱底端弯矩在时刻2.24 s出现峰值,最大值为1 223.09 kN·m,与最大层间相对位移的发生时刻相同。中柱底端的轴压力幅值为522.48 kN,出现最大值的时刻为12.18 s。由图11a 可以看出,中柱底部截面在地震荷载作用下的弯曲压应力幅值为8.49 MPa,弯曲压应力在时刻2.24 s 达到最大,静力荷载作用下柱底截面轴向压应力为9.74 MPa,两者相叠加得到中柱底部截面边缘压应力幅值为18.23 MPa,中柱的C45 混凝土轴心抗压强度设计值为21.1 MPa,由此可见柱底截面受压区混凝土边缘压应力幅值已达到规范规定的混凝土抗压强度设计值的86.4%,柱底截面边缘混凝土处于塑性屈服工作状态,局部可能出现混凝土压溃现象。由图11b 可以看出,侧墙与结构底板相交处截面仅承受地震荷载的弯曲压应力幅值为5.29 MPa,最大值出现的时刻为2.24 s,与静力荷载作用下侧墙与底板相交处截面轴向压应力相叠加为14.43 MPa,侧墙的C35 混凝土轴心抗压强度设计值为16.7 MPa,由此可见侧墙与底板相交处截面边缘压应力幅值已达到规范中混凝土抗压强度设计值的86.4%,侧墙底部截面边缘混凝土进入塑性屈服阶段,局部会出现压碎。

表3 El Centro波激励下结构关键部位内力响应幅值Tab.3 Internal Force Response Amplitude of Key Parts of Structure under El Centro Wave Excitation

图10 中柱底时程曲线Fig.10 Time History Curve at the Bottom of Middle Column
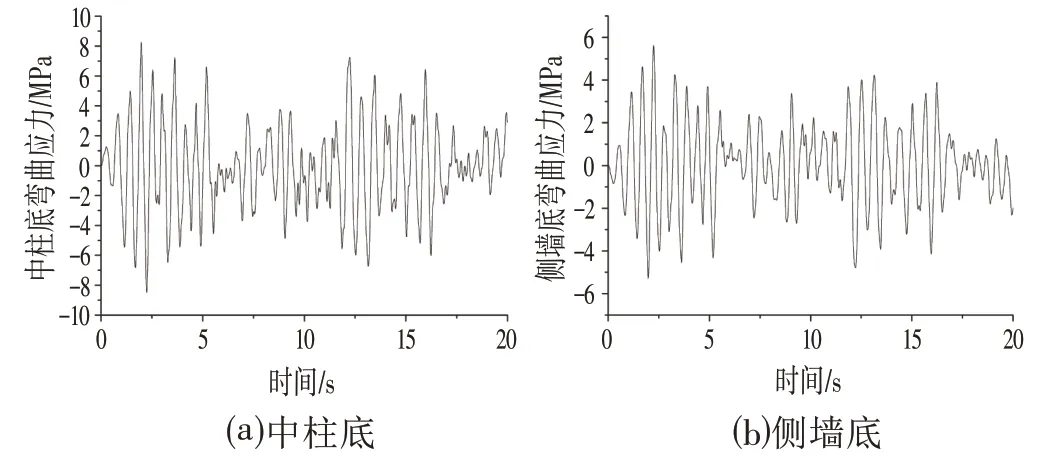
图11 弯曲应力时程曲线Fig.11 Time History Curve of Bending Stress
3.3.3 柱轴压比分析
柱轴压比是反映结构延性的重要参数,改善结构的抗震性能要求结构具有良好的延性。柱轴压比通过中柱与底板连接节点处的柱轴力最大值计算,永久荷载作用下和3种地震波激励下的中柱底端截面最大轴压力设计值及相应轴压比如表4 所示,永久荷载作用下的轴力通过施加结构自重和水、土压力计算,地震波激励下的柱底轴力采用永久荷载和地震荷载作用下的轴力荷载组合计算。
由表4 可以看出,考虑地震作用荷载组合的柱轴压比与仅承受静力荷载的柱轴压比相差不大,地震作用的影响较小,兰州波激励下的中柱轴压比最大,最大轴压比为0.610。根据《城市轨道交通结构抗震设计规范》,埋深超过20 m的地下车站结构,中柱设计轴压比的上限值为0.80。考虑地震作用荷载组合下的柱轴压比与规范限值接近,车站结构中柱延性较差,容易发生压碎破坏。
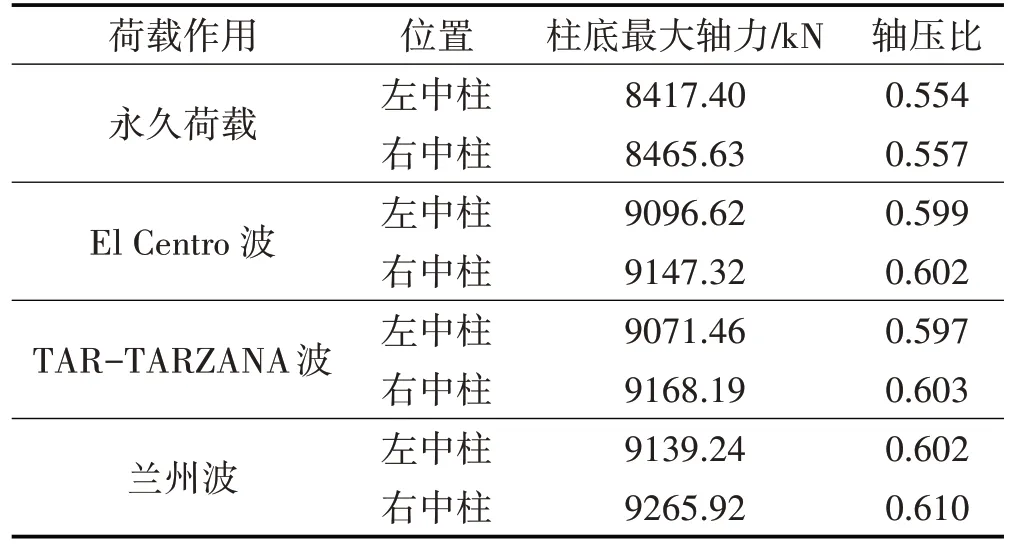
表4 中柱最大轴压力及轴压比Tab.4 Maximum Axial Pressure and Axial Pressure Ratio of Middle Column
4 结论
对地下车站结构进行抗震计算是地铁结构设计中的一项重要内容,关系到地铁结构在遭遇强震作用时的整体安全性。本文分别采用反应位移法和三维动力时程分析法对地铁地下车站结构进行地震响应分析,对重要结构构件的关键部位内力和变形进行了计算分析,得出了一些结论:
⑴ 车站结构正常使用阶段的各种荷载组合工况中,考虑地震荷载的偶然组合对结构内力不起控制作用;
⑵ 从采用反应位移法计算得到的结构在地震荷载激励下的内力响应结果可以看出,侧墙与各层楼板相交处、结构顶底板与中柱连接节点处弯矩和剪力较大,顶底板跨中有较大弯矩,中柱最大轴压力出现在中柱与底板连接位置;
⑶ 采用动力时程分析法计算地下车站结构的地震响应时,为保证结构抗震分析的可靠性和准确性,计算过程中选择输入的地震动加速度时程的反应谱曲线与适合本工程的设计地震动加速度反应谱曲线的误差满足规范规定的限值要求,使计算结果更接近结构真实地震响应;
⑷ 通过对地下车站结构施加3 条实际地震波激励进行三维动力时程分析,车站结构的最大层间相对位移及最大层间位移角在规范限值要求的范围内,结构整体抗侧向变形能力良好;
⑸ 地下车站结构中柱与顶底板连接部位、侧墙与顶底板相交处、结构顶底板与侧墙相交位置附近、各层楼板与中柱连接节点处、顶底板边跨跨中部位均在地震时程分析中出现了较大的内力响应,这些结构构件的关键部位均为抗震薄弱环节,需要通过加强抗震措施提高结构的抗震性能;
⑹ 中柱在地震荷载作用下的轴压比较大,与规范规定的中柱设计轴压比上限值接近,车站结构中柱的延性较差。
