饱和氩蒸气冷凝特性的分子动力学模拟

2

(1.大连理工大学 化工学院 ， 辽宁 大连 116024 ； 2.中北大学 机械与动力工程学院 ， 山西 太原 030051 ; 3.大连理工大学 化工机械与安全学院 ， 辽宁 大连 116024)

发生在气-液界面上的冷凝现象广泛存在于许多工程领域中，人们已经对其进行了一些理论探索和分子动力学(MD)模拟研究。TSURUTA等[1-2]根据过渡状态理论推导出冷凝系数的理论表达式，且该表达式与分子动力学模拟结果符合良好。王遵敬等[3-4]通过对氩和甲烷蒸气冷凝过程的分子动力学模拟研究发现，冷凝系数随着温度的升高而降低。孙杰等[5]对氩流体的气-液界面进行了较大温度跨度的分子动力学模拟，得到了温度对密度、气-液界面厚度、气相分子碰撞流率等的影响规律。拟采用分子动力学模拟技术，探讨气-液平衡条件下饱和氩蒸气的冷凝系数和冷凝活化能等变化规律。

1 模拟方法

1.1 模拟体系的建立

直角坐标系下的MD模拟盒子，如图1所示，液相位于模拟盒子的中部，气相分别处于模拟盒子的上下两侧，整个模拟体系中有两个气-液界面。对于氩流体，分子i和j间的相互作用势能函数(U)，如式(1)所示[6]。

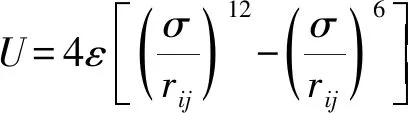
(1)

式中：rij为分子i和j之间的距离，ε为L-J能量参数，σ为L-J尺度参数。对于氩流体，σ=3.396 7×10-10m，ε=1.615 3×10-21J[6]。

1.2 模拟细节

模拟体系由4 000个氩分子组成。初始时刻，氩分子以饱和液体状态按照面心立方(FCC)方式排布于模拟盒子的中部，上下两侧为真空区域，作为气相区，粒子初始速度随机给定。为使体系不发生宏观运动，模拟过程中不断调整质心位置及体系总动量，使质心位置处于坐标原点，体系总动量为零。截断半径rc=4σ(σ为氩分子的尺度参数)。时间步长Δt=4.331×10-15s，z方向划分300薄层用于统计密度分布。在模拟过程中，x、y、z方向均采用周期性边界条件。采用NVT系综，Woodcock变标度法实现恒温控制，Velocity-Verlet法来求解牛顿运动方程。模拟过程共运算13万动力学步，前3万步用来实现气-液平衡。待系统平衡后，开始统计体系的冷凝特性。本文所用模拟程序为本课题组采用Fortran语言自行编写。算法流程见图2。

2 结果与讨论

2.1 气-液界面厚度

采用MD模拟方法，计算得到不同温度(T)和气-液平衡条件下氩流体的密度(ρ)，分布曲线见图3；气-液界面厚度(δ)如表1所示。本文取密度为液相主体密度的95%处为液相主体与气-液界面区的分界面，记为zl。气相主体密度的105%处为气相主体与气-液界面区的分界面，记为zg与zl；气-液界面厚度为zg与zl之差。由表1和图3可见，随着温度的升高，气-液界面厚度逐渐增大。

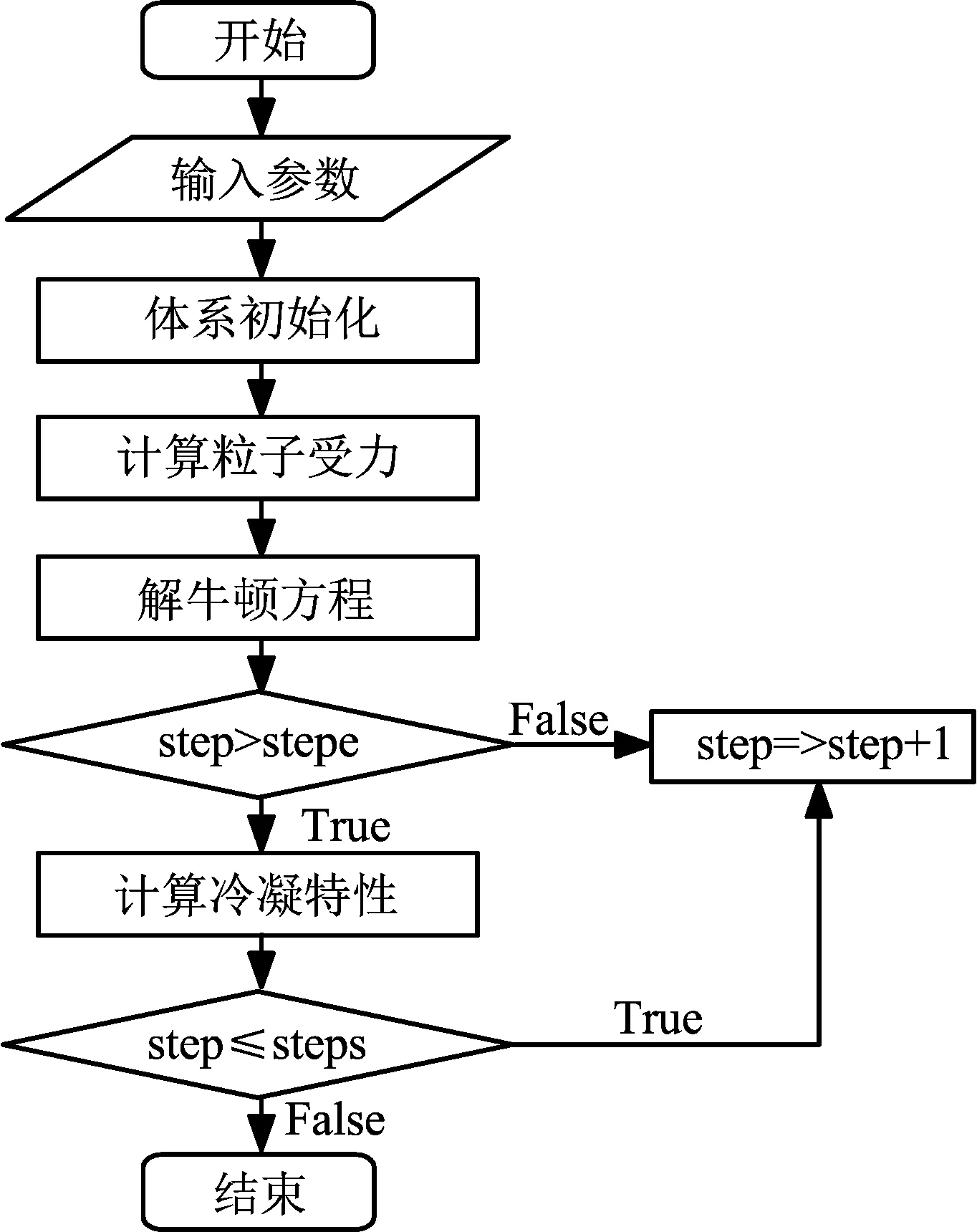
(注：stepe为平衡步数；steps为总运算步数)图2 饱和氩蒸气冷凝特性的MD模拟流程简图

图3 密度分布与温度的关系曲线表1 温度对气-液界面厚度的影响

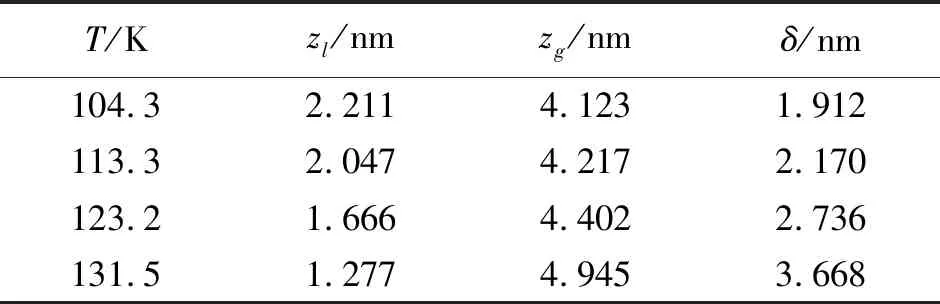
T/Kzl/nmzg/nmδ/nm104.32.2114.1231.912113.32.0474.2172.170123.21.6664.4022.736131.51.2774.9453.668

2.2 冷凝系数

冷凝系数(α)为冷凝通量(Jcon)与分子碰撞通量(Jcoll)之比，如方程(2)所示[7]。

(2)

当温度较低时，饱和氩蒸气可以近按理想气体处理，碰撞通量可以利用Hertz-Knudsen (HK)方程计算得到[7-8]。

(3)

式中：M为摩尔质量，p为压力，R为普适气体常数。

为采用分子动力学方法，统计粒子的碰撞通量(由于气-液界面区域是不断起伏变化的，本文认为粒子一旦离开气相主体，即可视为发生了碰撞)，引入一自相关函数σi(t)[7-8]：

(4)

式中：V为汽相主体区域，t为时间。

则碰撞通量(Jcoll)为[7-8]：

(5)

式中：<>为系综平均(对于MD模拟，即为时间平均)。

表2 碰撞通量的理论计算值与MD模拟值比较

当气相中的粒子与气-液界面发生碰撞后，z方向速度大的粒子将进入液相区域成为冷凝粒子；而z方向速度小的粒子则被反弹回到汽相区域成为反弹粒子。图4与图5分别给出了温度为104.3 K时，冷凝粒子与反弹粒子的位置随时间的变化(图中给出的时间为分子动力学步)。

图4 冷凝粒子位置随时间的变化(104.3 K)

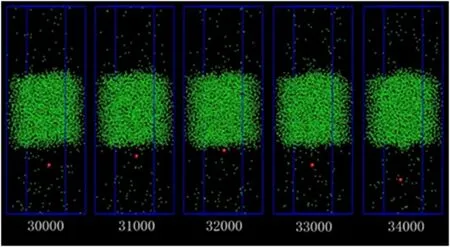
图5 反弹粒子位置随时间的变化(104.3 K)

本文采用文献[8]的统计方法，来计算氩流体气-液平衡条件下的冷凝系数。文献[8]认为，冷凝粒子与反弹粒子在液相(液相主体+气-液界面区域)内的停留时间不同。当粒子在液相中的停留时间大于特征时间(tA)时，则该粒子被认为是冷凝粒子；否则，则视为反弹粒子。图6给出了温度为131.5 K时，碰撞粒子数目(N)在液相中停留时间的变化曲线。由图6可以发现，曲线可以分为两个部分，前段曲线迅速降低，而后段则较为平坦，两段的交点即为特征时间(tA)，这一趋势与文献[8]的结果一致。特征时间所对应的粒子数目即为冷凝粒子数目，停留时间t=0处所对应的粒子数目即为碰撞粒子数目。利用方程(2)即可求得该温度下的冷凝系数(α)。不同温度下的冷凝系数与文献值的比较，如图7所示。由图7可以看出，在模拟温度范围内本文所得冷凝系数介于0.796和0.439之间，且随着温度的升高而降低，其变化趋势与文献[2-3]基本一致。

图6 碰撞粒子数目随停留时间的变化曲线(131.5 K)

图7 不同温度下冷凝系数与文献值的比较

2.3 冷凝活化能

分子碰撞理论认为，并不是所有反应物分子之间的碰撞均会转化为生成物分子，只有具有足够动能且碰撞方向正确的分子间的碰撞才有可能发生反应，具有足够能量的分子称为活化分子，化学反应活化能可以认为是活化分子平均动能与反应物分子平均动能之差[9]。

文献[1]认为，在冷凝过程中，只有具有足够能量且运动方向正确的气相分子，才有可能越过能垒进入液相而成为冷凝粒子，因此，冷凝过程可以视为一种特殊的化学反应过程，冷凝粒子即可认为是化学反应中的活化分子。本文将冷凝分子的平均动能()与气相分子的平均动能()之差，视为冷凝活化能(Eα)，即：

Eα=-

(6)

在不同温度下，冷凝粒子与饱和蒸气的平均动能的MD模拟结果，如表3所示。冷凝活化能与温度的关系曲线如图8所示。

表3 不同温度下冷凝粒子及饱和蒸气的平均动能

图8 冷凝活化能与温度的关系曲线

由图8可见，冷凝活化能随着温度的升高而增大，但增幅逐渐减小，说明温度越高气体冷凝越困难，这与宏观冷凝现象一致。冷凝活化能与汽化潜热及温度密切相关，三者的关系符合方程(7)[7]。

Eα=Eαc-ΔHm·Trexp(-11Tr+lnTc)

(7)

式中：Eαc为临界温度所得对应的冷凝活化能，Tr为对比温度；ΔHm为气化潜热，可利用方程(8)计算得到[10-11]。

(8)

式中：n为指数因子，n=0.38；Tb为沸点温度；ΔHm,b为沸点温度所对应的气化潜热。

冷凝系数与冷凝活化能的关系可以采用Arrhenius方程(9)描述[7]。

α=k0exp(-Eα/RT)

(9)

不同温度下的冷凝系数α、冷凝活化能Eα、指前因子k0，如表4所示。由表4可以看出，指前因子总体而言随着温度的升高而降低。

表4 不同温度下冷凝系数α、冷凝活化能Eα、指前因子k0

3 结论

采用分子动力学模拟技术，探讨气-液平衡条件下饱和氩蒸气的冷凝特性。模拟结果表明，随着温度的升高，气-液界面厚度逐渐增大，冷凝系数有所降低。冷凝活化能随着温度的升高而增加，但增幅逐渐变小。冷凝系数与冷凝活化能之间的关系可以用Arrhenius方程来描述。