基于多目标规划模型的黑河中游绿洲用水结构优化配置

王友芝 郭 萍

(中国农业大学中国农业水问题研究中心， 北京 100083)

0 引言

黑河中游绿洲是鹰落峡水文站和正义峡水文站之间的冲击平原，其行政区主要包括甘州区、临泽县和高台县，用水部门主要包括农业、工业、生活和生态部门[1]。目前，水资源短缺、用水结构不均衡、水资源利用效率低及生态环境恶化制约着社会经济发展。随着气候变化以及极端天气的不断加剧，水资源配置系统面临着复杂风险，产生了一系列的效益损失。因此采取战略措施，规避水资源系统面临的风险，对于保证各用水部门的协调发展和水资源可持续利用具有重要意义。

水具有资源、环境、社会和经济等多个属性，因此水资源优化配置需兼顾水资源的经济、社会、环境等属性。为了解决上述问题，很多学者采用多目标规划方法来配置水资源[2-3]。由于气候、人类活动等影响，水资源配置系统的不确定性增大，加剧了系统存在的风险。以往的研究较少考虑水资源配置过程中存在的风险或者对供水风险进行量化，忽略了用水结构不合理的风险[4-5]。因此，有学者采用结构性缺水风险指数[6]来指导水资源配置。但是以往的研究通常将结构性缺水风险用于后优化分析，其过程繁琐，且不能实现风险与配水的交互过程。因此，本文将结构性缺水风险指数作为目标来指导水资源的优化配置。公平性是水资源优化配置的重要指标，目前配水公平性已由定性研究转向定量研究。很多研究将GINI系数作为公平性指标应用在约束条件或者目标函数上，用于指导水资源配置[7-8]。另外，经济效益一直是水资源优化配置的首要目标，是保障社会发展的基本条件。经济效益、缺水风险和社会公平性是相互矛盾的目标，而这三者往往是决策者需考虑的因素，因此，将配水产生的经济效益、结构性缺水风险和公平性作为多目标进行配水优化是需要解决的问题。

可利用水量是水资源配置系统的一个重要指标，但由于气候变化、人类活动等影响，其变化规律复杂，具有很强的不确定性。很多学者采用模糊方法对可利用水量进行了定量表征，并在不确定条件下对水资源进行优化配置[9-11]。但是，在实际配水过程中，决策者的乐观、悲观态度往往对配水结果产生较大影响。Me测度作为一种不确定性方法，能够反映决策者的态度，根据不同的乐观-悲观因子将Me测度转换为可能性测度、必要性测度和可行性测度[12-14]。因此本文引入Me测度，通过不同的乐观-悲观因子以及测度置信水平反映决策者的态度，获得不同态度及置信水平下最优的配水方案[15]。

本文首先构建确定条件下的水资源多目标优化模型，然后构建基于Me测度约束的多目标优化模型，最后将模型应用于黑河中游区域用水结构优化。通过比较配水量和目标值的结果选择更适合本地区用水结构优化模型，为该区域部门间水资源优化配置提供科学方法。

1 模型建立

1.1 多目标规划配水模型

以结构性缺水风险指数为目标，它是区域缺水程度与用水结构均衡的风险性指标，由缺水风险和用水结构风险共同决定。其中，用水过程中产生的结构性风险通过用水结构信息熵体现；用水过程中产生的缺水风险由缺水指数度量。其表达式为[6]

(1)

其中

(2)

(3)

式中G——结构性缺水指数

Wc——缺水指数

S——用水结构信息熵

x——实际用水量

Wa——历史年份中该区域用水量的最小值

Wm——历史年份中该区域用水量的最大值

由式(1)可看出，用水结构信息熵越大，则说明区域用水结构越均衡，进而区域结构性缺水指数越小；由式(2)、(3)可看出，缺水指数利用历史年份的最大、最小用水量反映了本次用水的变化程度，即区域用水量越大，就越有可能造成区域缺水情况，相应地，结构性缺水指数也越大。

以各部门配水产生的净经济效益为经济目标，模型表达式为

(4)

式中Bij——净效益系数

Xij——配水量Cij——成本

以GINI系数作为衡量部门间配水公平性的指标，将GINI系数最小化作为目标。其表达式为

(5)

式中n——区域个数

i1、i2——区县，取值1～3，分别表示甘州区、临泽县、高台县

GINI系数取值范围为0～1,0表示绝对公平，1表示绝对不公平，其越接近0表明收入分配越是趋于平等。通常将0.2以下视为绝对平均；0.2～0.3视为比较平均；0.3～0.4视为收入相对合理；0.4～0.5视为差距较大，0.5以上表示差距悬殊[16]。

1.2 基于Me测度的多目标配水优化模型

目标1为风险目标(式(1))，目标2为经济目标(式(4))，目标3为社会目标(式(5))。

由于水资源配置系统中，可利用水量具有模糊特性，因此采用模糊数对可利用水量进行定量表征。常用的模糊数处理方法为测度法，包括可能性测度、必要性测度和可信性测度。但是上述方法均存在各自的缺陷，且仅采用其中一种方法不能反映整体的情况。但是Me测度却能整合所有的情况，而且还能反映决策者的风险偏好，通过可能性、必要性测度以及乐观-悲观调整因子进行构建，其表达式为

Me{ξ≤r}=Nec{ξ≤r}+λ(Pos{ξ≤r}-Nec{ξ≤r})

(6)

其中

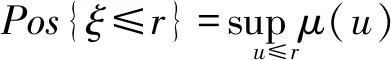
式中λ——乐观-悲观调整参数,0≤λ≤1

Nec——必要性测度

Pos——可能性测度

ξ、μ——决策变量r——实数

μ(u)——隶属度函数

(7)

根据式(7)可知，当λ取1时，Me测度转换为可能性测度(Pos)；当λ取0时，Me测度转换为必要性测度(Nec)；当λ取0.5时，Me测度转换为可信性测度(Cr)；以λ取值的3种情况为例，对模型进行求解[5]。

当λ=1时，Me等于Pos，表示决策者的态度是积极的，即

则

r≤ξ2+(1-γt)(ξ3-ξ2)

(8)

当λ=0时，Me等于Nec，表示决策者的态度是消极的，即

则

r≤ξ2-γt(ξ2-ξ1)

(9)

当λ=0.5时， Me等于Cr，表示决策者持有折衷的态度，即

则

r≤ξ2+(1-2γt)(ξ2-ξ1)

(10)

γ通常取值大于0.5[17]。根据定义，可以得到

(11)

采用不同的γ对上述约束作为3种情景进行求解，比较不同测度方法对于求解结果的影响。

1.3 模型求解

对于多目标模型，采用多目标转换为单目标的方法进行求解，公式为[7]

(12)

其中

v1+v2+v3=1

式中v1、v2、v3——目标g1、g2、g3的权重

权重组合一共有36种组合方式[7]。

2 实例研究

2.1 研究区概况

研究区位于黑河流域中游张掖市，主要包括甘州区、临泽县和高台县，属于内陆干旱气候。年均降水量为140 mm，年均蒸发量为1 400 mm，蒸发量远大于降水量，水资源短缺严重[18-19]。在有限的可利用水量条件下，部门间不合理的用水结构加剧资源浪费，且容易引起缺水风险。不同区域同一部门间水资源分配的不合理性不利于社会、经济的可持续发展。因此，对研究区的用水结构进行优化，以实现区域公平可持续发展。研究区如图1所示。

图1 研究区域

2.2 配水优化模型

(1)目标函数

目标1为结构性缺水风险最小，即

(13)

目标2为经济效益最大，即

(14)

目标3为公平性最大，即

minf3=m+f+t+s

其中

(15)

式中m——农业部门GINI系数

f——工业部门GINI系数

t——生活部门GINI系数

s——生态部门GINI系数

W——各地区各部门的配水量，m3,为决策变量

i——地区，i取1、2、3，分别表示甘州区、临泽县、高台县

j——用水部门，取值1、2、3、4，分别表示农业部门、工业部门、生活部门和生态部门

B——净效益系数，元/m3

C——配水成本，亿元

Wmin——历史年份中该区域的最小用水量，m3

Wmax——历史年份中该区域的最大用水量，m3

Q——可利用水量，m3

A——农业灌溉面积，hm2

E——工业经济效益，元

P——人口数

Ae——生态灌溉面积，hm2

(2)约束条件

可利用水量约束为

(16)

情景2

(17)

情景3

(18)

情景4

(19)

需水约束为

Wij,min≤Wij≤Wij,max(∀i,j)

(20)

非负约束为

Wij≥0 (∀i,j)

(21)

情景1指原始的可利用水量约束；情景2是必要性约束；情景3是可能性约束；情景4是可信性约束。对4种情景分别进行求解，比较分析不同测度约束情景下配水量和目标值差异，为决策者提供更多的备选方案。

2.3 模型参数确定

历年最小最大需水量、农业灌溉面积、工业经济效益、人口数以及生态灌溉面积从2013年张掖市统计年鉴获得；配水净效益以及配水成本采用LI等[20]数据；可利用水量的确定方法如下：历年可利用水量的均值作为三角模糊数的最可能(取)值(中间值)，最小可能(取)值(下界)和最大可能(取)值(上界)采用95%的置信区间。置信区间是根据历年的可利用水量数据，采用区间估计的方法获得。历年可利用水量的数据从2013年张掖市水利年报获取。张掖市统计年鉴和水利年报均从调研数据中获得。表1、2为配水净效益系数、成本、各部门最大最小需水量以及灌溉面积、工业产值、人口数据和可利用水量数据。

表1 各用水部门的净效益系数、成本、最大最小需水量

表2 用水部门灌溉面积、工业产值、人口数、生态灌溉面积和可利用水量

3 结果与分析

按照前述模型解法，求解确定条件下多目标配水优化模型和不确定条件下基于Me测度的多目标配水优化模型，获得不同目标权重下的配水方案和目标值以及不同测度水平下的配水方案和目标值。比较确定条件下多目标配水优化结果与单目标优化配水结果，确定条件下多目标与不确定多目标配水优化结果，不确定多目标不同约束的配水优化结果。

3.1 确定多目标配水优化结果

除v1=0.1、v2=0.1、v3=0.8一种组合外，其他35种组合的各部门配水量及目标值相同，这是由求解方法的性质决定的。当v1=0.1、v2=0.1、v3=0.8时，多目标求解过程中优先考虑风险目标，其次考虑经济目标和社会目标，所以总的配水量较其他权重组合下的水量少，GINI系数较其他权重组合的高，后续会与其他权重组合进行比较。当v1=0.1、v2=0.2、v3=0.7时，配水过程中不再优先考虑风险目标，而是调整相应部门的配水实现3个目标值的均衡。以权重v1=0.1、v2=0.2、v3=0.7的多目标配水结果与单目标配水结果进行比较，结果如图2所示。

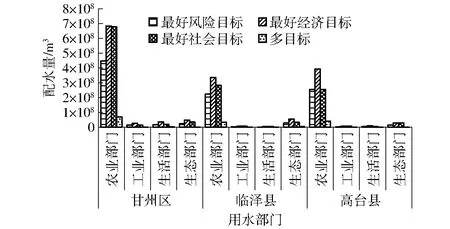
图2 不同模型下的各区域各用水部门的配水量

最好风险目标的配水结果为各用水部门配水达到其最小配水量。这是由该目标的性质决定的，即在满足其他约束条件下，配水越少，缺水风险指数越小。最好经济目标配水结果表现为工业部门、生活部门和生态部门均达到了其最大需水量，农业部门的配水量介于最小需水量和最大需水量之间。这是因为在有限的水量条件下，水量优先分配给净效益高的部门。最好社会目标的结果表现为配水量与其对应的农业灌溉面积、工业产值、人口数、生态灌溉面积成正比。以农业部门为例，甘州区的灌溉面积最大，临泽县的灌溉面积居中，高台县的灌溉面积最小。相应地，在满足最小需水量的条件下，配水量也表现为相同的变化趋势，即甘州区的配水量最大，临泽县的配水量居中，高台县的配水量最小。其他用水部门也表现为类似的变化趋势。这是由社会目标的性质决定的，即同一用水部门在不同区域间配水的公平性。相较于单目标优化配水结果，多目标优化配水则得到了一个折衷的结果。为了更明显地突出多目标配水结果的折衷性，比较多目标模型配水较3个单目标模型配水的变化百分比，结果如表3所示。

表3 单目标和多目标优化配水量及配水变化百分比

用水部门水量变化百分比为0，表示多目标优化配水保留了与单目标相同的水量；否则，表示多目标优化配水调整了该部门的配水以适应其他目标的变化。以多目标较风险单目标配水变化比例为例，甘州区的生态部门配水的变化百分比为0，相应地，该部门对应于经济单目标和社会单目标的配水量减少了50%和33.69%，这是因为在优化过程中，多目标以牺牲该部门的经济效益和社会效益来实现其风险效益。临泽县的工业、生活部门以及高台县的工业、生活、生态部门表现出类似的变化规律。以多目标较经济单目标配水变化百分比为例，甘州区的工业部门的配水变化百分比为0，该部门对应于风险目标和社会目标的配水量都增加了100%，即工业部门的配水量满足了其最大需水量。在水量优化配置过程中，多目标以牺牲该部门的风险效益和社会效益来实现其经济效益。甘州区的生活部门和临泽县的生态部门呈现相似的变化规律。以多目标较社会单目标配水变化百分比为例，各部门的配水均发生了变化。除去相应于其他目标配水变化百分比为0的其他部门外，农业部门的配水比例呈现增加趋势。多目标优化以风险目标和经济目标为重，社会目标配水产生相应的变化，这是因为社会目标的权重(最优值减最差值后的倒数)较前两个单目标的权重小，因此在配水过程中，最后考虑社会目标。从总配水量来看，风险目标和经济目标的总配水量分别达到1.038×109、1.638×109m3,社会目标总配水量介于两者之间，为1.373×109m3。多目标优化配水的配水量为1.638×109m3。多目标配水优化总配水量和经济单目标的总配水量相同，但是效益却不相同。将多目标产生的各目标值与单目标产生的目标值进行比较，结果如表4所示。

多目标优化各目标值处于一个折衷的结果。其目标值处于各单目标求解效益的最优值和最差值范围内。单目标的目标值偏重于单一方面，可靠性偏低。风险单目标配水优化中，结构性缺水风险最优值为0，表明各产业用水结构较好且缺水风险较低。但是其经济效益偏低，不利于经济发展；经济单目标配水优化中，经济效益达到了最大值，总社会目标值(农业、工业、生活、生态部门GINI系数的和)也较小，但是相较于多目标优化配水的结果，其灵活性较低。因为在多目标优化过程中，决策者可以根据不同的目标权重获得不同的配水方案，具有较多的选择性。比如，当各目标的权重取值为v1=0.1,v2=0.1,v3=0.8时，风险值为0.83，效益值为3.14， GINI为1.01。社会单目标配水优化中，其GINI系数最小，表明地区间同一部门的配水处于公平状态，但是其风险系数较大，存在一定的缺水风险和同一区域内产业间配水不合理的问题。另外，其经济效益相对偏低，不利于经济发展。综上所述，单目标求解的配水量和目标值均包含于多目标求解的结果里，即多目标结果具有更高的可靠性和鲁棒性。决策者可以根据偏好(即目标权重)获得配水方案和目标效益。

3.2 不确定性条件下基于Me测度的多目标配水优化结果

取v1=0.1、v2=0.2、v3=0.7，乐观-悲观因子参数λ=0.1、0.5，测度水平参数γ=0.7、0.9、1，所得的配水结果和效益如表5所示。

表5 基于Me测度的多目标优化模型配水量

甘州区的工业部门、生活部门以及临泽县的生态部门达到了其最大需水量。除了农业用水部门外，其他部门的配水量满足了其最小需水量。另外，除农业用水部门外，其他部门的配水量不受乐观-悲观调整参数以及测度水平参数的影响。因此，仅分析农业部门配水对上述两个参数的响应规律。从甘州区总的可利用水量来看，以γ=0.7为例，必要性测度约束下的配水量最小，可信性测度约束的配水量居中，可能性测度约束的配水量最大，这是由测度性质决定的。而且，各地区总的配水量及其他测度水平也表现为上述规律。另外，3种测度约束条件下，农业部门的配水量随着测度水平的增加而较低，即配水量与测度水平呈现相反的变化趋势。这是因为测度水平越高，可利用水量越少，约束满足的水平越高。不同的测度水平表示模糊数距离最大可能值的程度。以必要性测度为例，测度水平越高，可利用水量偏离其可能值的程度越高。可利用水量随着测度水平的增加从最可能值趋于最小可能值，可利用水量呈现减少趋势，进而约束满足的置信水平越高；以可能性测度为例，测度水平越高，可利用水量接近其可能值的程度越高。可利用水量随着测度水平的增加从最大可能值趋于最可能值。水量由大到小，置信水平由小到大；以可信性测度为例，当测度水平大于等于0.5时，可利用水量偏离其可能值的程度越高。当测度水平等于1时，必要性测度和可信性测度的配水结果相同。

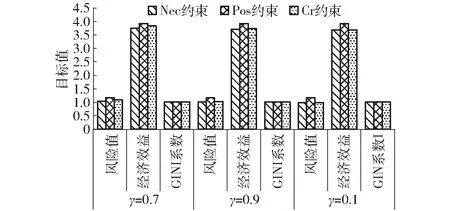
图3 不同约束情景下的多目标值

不同测度约束条件、不同置信水平下的目标值如图3所示。由图可知，3种测度约束的同一目标值随着测度水平的变化呈现相同的变化规律。即风险值和经济效益随着测度水平的增加而减小，GINI系数随着测度水平的增加而增大。原因在于随着测度水平的增加，可利用水量减少，结合单目标规划的结果可知，经济效益和风险值与配水量成正比， GINI系数与配水量成反比，所以当置信水平增大，可利用水量减少时， 风险值和经济效益减少，GINI系数增大。同置信水平下，各目标值在不同测度约束下表现出不同的变化规律。以风险值和经济效益为例，当γ=0.7时，Pos约束的风险值和经济效益 (1.17, 3.92)最大，Cr约束的风险值和经济效益 (1.09, 3.83)居中，Nec约束的风险值和经济效益 (1.04, 3.75)最小。以GINI系数为例，Pos约束的GINI系数最大，Cr约束的GINI系数居中，Nec约束的GINI系数最小。原因在于同一置信水平下，不同测度约束下可利用水量由大到小依次为Pos约束、Cr约束、Nec约束，结合各目标与配水量的关系，可以得到上述结果。γ=0.9和γ=0.1时，目标值也表现为相似的规律。由上述结果可以推断出，在求解最小目标时，必要性测度约束优于另外两种测度约束；在求解最大目标时，可能性测度约束优于其他两种测度约束。可信性测度约束则能折衷两种约束的结果。

3.3 优化结果比较

从配水、效益角度对确定性多目标模型和不确定性多目标模型加以比较。由于不同的测度约束条件下配水量及目标值随着不同约束置信水平的变化规律相同，因此，仅选择一种置信水平进行比较。以γ=0.7为例，将两个模型的配水量和目标值结果进行比较，结果如图4、5所示。

图4 不同约束情景下的各区域总配水量

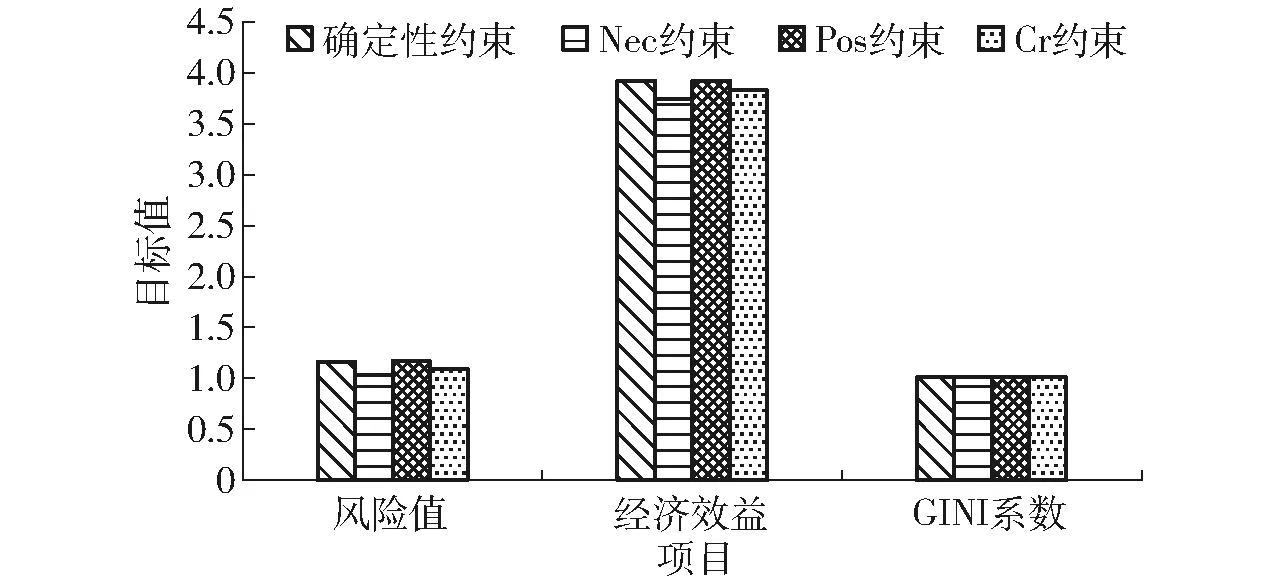
图5 不同约束情景下的各目标值

以甘州区总配水量为例，配水量由大到小依次为Pos约束、确定性约束、Cr约束、Nec约束。临泽县和高台县总配水量表现为相同的趋势。风险值由大到小依次为Pos约束、确定性约束、Cr约束、Nec约束。这是因为风险值与配水量成反比，配水量越多，缺水风险越高或者配水结构越不均衡。经济效益由小到大为Pos约束、确定性约束、Cr约束、Nec约束。原因在于经济效益与配水量成正比，配水量越多，经济效益越大。GINI系数由大到小为Nec约束(1.102 8)、Cr约束(1.102 5)、确定性约束(1.102 1)、Pos约束(1.102 0)。这说明随着配水量的增加，GINI系数呈现减少趋势，同时意味着农业部门的配水还未达到其理想的公平状态。因此，当配水量增大时，GINI系数变小。相较于确定性多目标优化配水模型，基于ME测度的多目标优化配水模型能够反映决策者不同的态度和对于约束的满意程度，且其配水结果及目标值包含确定性模型的结果。另外，其能产生不同态度、不同置信水平下的配水方案集，为决策者提供更多的选择，具有更高的鲁棒性。

本文提出了确定性多目标规划和不确定条件下基于Me测度的多目标规划。相较于以往的研究，创新点主要有：①引入结构性缺水风险指数，衡量区域程度和用水结构均衡程度，并将其作为目标函数指导水资源优化配置，实现风险与配水的交互，衡量区域内用水结构均衡程度。②引入公平性GINI系数，衡量区域间同一产业的用水结构均衡程度。③引入Me测度，对可利用水量进行不确定性定量表征，考虑决策者的主观意愿。决策者可以根据自己的乐观-悲观态度以及对约束的满意程度选择合适的配水方案。

4 结论

(1) 综合考虑了配水的多功能属性，将配水产生的经济效益、配水公平性和结构性缺水风险考虑在内，采用确定多目标规划和不确定性条件下基于Me测度的多目标配水优化模型对甘州区、临泽县和高台县的农业、工业、生活、生态部门进行配水。

(2) 将确定条件下单目标规划和多目标规划进行比较，结果表明，多目标规划的配水量和目标值能够获得折衷的结果，且较单目标规划具有更强的灵活性。

(3) 将确定性条件下的多目标配水优化模型和不确定条件下的多目标配水优化模型进行比较。结果表明，确定性条件下的配水结果和目标值包含不确定性条件下的结果，说明不确定条件下基于Me测度的多目标配水优化模型具有更高的鲁棒性。

(4) 将不确定条件下不同约束的配水量和目标值进行比较，结果表明：从总配水量角度分析，必要性测度最小，可信性测度居中，可能性测度最大；从结构性缺水风险值分析，必要性测度最小，可信性测度居中，可能性测度最大；从经济效益分析，必要性测度最小，可信性测度居中，可能性测度最大；从GINI系数角度分析，必要性测度最大，可信性测度居中，可能性测度最小。另外，3种条件约束下，配水量、结果性缺水风险值、经济效益均随着测度水平的增加而减小，GINI系数随着测度水平的增加而增大。 因此，决策者可以根据风险偏好、乐观-悲观因子和测度水平选择合适的配水方案。