行星轮系水稻钵苗移栽机构正反求设计方法研究

吴国环 俞高红 叶秉良 俞亚新

(1.浙江理工大学机械与自动控制学院， 杭州 310018； 2.温州职业技术学院机械工程系， 温州 325035；3.浙江省种植装备技术重点实验室， 杭州 310018)

0 引言

水稻钵苗移栽具有缓苗期短、秧苗损伤小、对气候具有补偿作用等优点，可以有效地实现省种、增产和增收。因此，水稻钵苗移栽技术具有很好的发展前景[1]，当前已有大量关于水稻钵苗移栽机构的研究[2-5]。日本井关农机株式会社研发了一种有序移栽机，其移栽装置复杂、成本高，不适合中国国情。吉林省延吉市光华机械厂研制的串联四杆机构水稻钵苗移栽机[6]、吉林鑫华裕农业装备有限公司和东北农业大学联合研发的拟合齿轮五杆水稻钵苗移栽机构[7-8]，均以连杆机构作为核心传动机构，移栽效率低、工作时机构振动大，制约了其应用和推广。延边大学研发了非圆齿轮行星轮系水稻钵苗摆栽机构[9]和旋转式水稻钵苗夹摆秧机构[10]，两种机构的植苗方式均靠苗自身重力落入水田，故立苗率不佳；吉林大学研发了五齿轮钵苗移栽机构[11]，种植的秧苗直立度差；东北农业大学研发了B样条非圆齿轮行星轮系水稻钵苗移栽机构[12]，浙江理工大学研发了旋转式行星轮系水稻钵苗移栽机构[13]、非圆-不完全非圆齿轮行星轮系水稻钵苗移栽机构[14]，以上几种移栽机构具有效率高、振动小的优点，但动轨迹(即移栽机前进作业时，移栽臂秧针尖点生成的轨迹)前倾明显，容易将栽植好的秧苗推倒。因此，现有旋转式行星轮系移栽机构能高效移栽，但存在不能同时具备良好的移栽姿态和轨迹的问题。故研究行星轮系水稻钵苗移栽机构的设计方法，使其能够同时满足移栽轨迹和姿态要求具有重要意义。

目前，行星轮系水稻钵苗移栽机构的设计方法主要为正向设计和反求设计。正向设计方法[13-19]中非圆齿轮的节曲线方程是预先确定，它能够获得良好的移栽臂工作姿态，但在移栽轨迹上存在进一步优化的空间；反求设计是先给定理想的移栽静轨迹(移栽机不作业时，移栽机构旋转，移栽臂秧针尖点生成的轨迹)，反向求解行星轮系的总传动比，最后确定非圆齿轮节曲线及机构参数[20-22]。该设计方法可以保证移栽轨迹是理想的工作轨迹，但很难保证获得较好的移栽臂姿态。

为了设计出能够同时满足移栽姿态和轨迹要求的行星轮系水稻钵苗移栽机构，本文结合正向设计和反求设计的优点提出正向设计与局部轨迹微调的反求设计相结合的设计方法，简称正反求设计方法。由于在前期已经开展了正向设计研究[14]，本文在文献[14]的基础上，进一步开展局部轨迹微调的反求设计，综合设计非圆齿轮行星轮系水稻钵苗移栽机构，验证该方法对解决当前行星轮系水稻钵苗移栽机构设计局限问题的有效性。

1 正反求设计方法

正反求设计方法主要由正向设计和反求设计两大部分组成，反求设计是在正向设计基础上进一步优化设计，正向设计重点在保证移栽姿态(取秧角、推秧角)满足设计要求，反求设计重点在保证移栽动轨迹满足设计要求。首先利用正向设计获得具有满足姿态要求的移栽静轨迹，然后在保证取秧位置和推秧位置移栽臂移栽姿态不变的前提下，局部调整正向设计得到的静轨迹使得其动轨迹满足设计要求，基于调整后的静轨迹开展反求设计，综合两步设计得到最终的移栽机构。设计流程如图1所示。

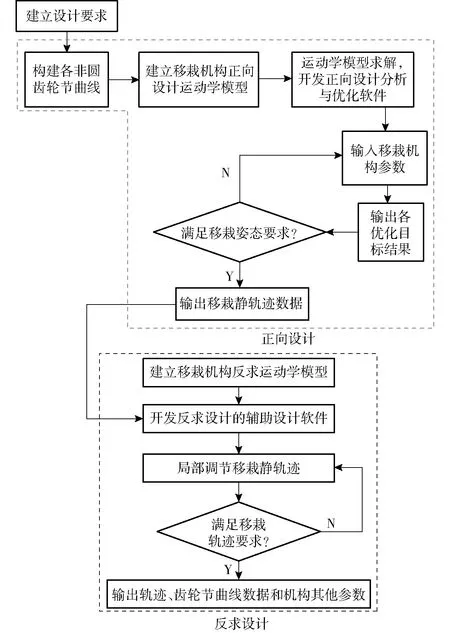
图1 正反求设计方法流程图

2 行星轮系水稻钵苗移栽机构设计

以非圆齿轮行星轮系水稻钵苗移栽机构的设计为例，说明正反求设计方法的实现过程。

2.1 机构工作原理与设计要求

移栽机构的工作原理如文献[14]所述，水稻钵苗移栽机的移栽臂模拟人手将钵苗从钵盘中取出，运送到推秧位置快速将秧苗推出插入水田土中完成秧苗的移栽。非圆齿轮行星轮系水稻钵苗移栽机构简图如图2所示，当移栽机不前进作业时，移栽机构旋转一周，移栽臂秧针尖点A′形成静轨迹ABCDEFG，其中A为轨迹最高点、B点为轨迹交点、C点为推秧位置点、D点为轨迹的最低点、F点为离行星架回转中心距离最近的点、G点为离行星架回转中心距离最远的点(即取秧位置点)。当移栽机构工作时，行星架7匀速顺时针转动，第一中间非圆齿轮3和太阳轮6无齿部分啮合时，凹锁止弧13和凸锁止弧5接触，使得第一中间非圆齿轮3相对于行星齿轮架7静止，这个过程中移栽臂秧针尖点A′形成轨迹ABCD(轨迹ABC为持苗轨迹段)，在轨迹点C处推秧至土中。当第一中间非圆齿轮3与太阳轮6有齿部分啮合时，第二中间非圆齿轮4与行星非圆齿轮2啮合并相对行星架7作非匀速转动；移栽臂14在DEF段和FGA段均相对行星架7作非匀速转动，分别形成回程段轨迹和取秧段轨迹。在取秧位置(轨迹右侧离回转中心最远点G处)，为了防止移栽臂秧针与秧苗其他部位接触，移栽臂应从秧苗下部靠近钵盘，夹住秧苗茎秆根部实现取苗，轨迹右上角形成“环扣状”取秧轨迹。

图2 非圆齿轮行星轮系水稻钵苗移栽机构简图

图3 移栽轨迹简图

为了使移栽机构能够实现上述工作原理，提出如下设计要求。规定移栽机移栽作业行进方向为右侧，每个移栽臂移栽速度为100株/min，株距H(两株秧苗之间的距离)为200 mm。移栽臂旋转一周的静轨迹和动轨迹如图3所示。结合图2和图3分析在设计水稻钵苗移栽机构时，必须要满足的设计要求，例如：环扣轨迹、取秧角、推秧角、推秧角与取秧角的角度差、轨迹高度及移栽动轨迹的回程段轨迹，具体见表1。

(1)环扣轨迹尺寸包含环扣高度和环扣宽度，移栽静轨迹环扣高度即取秧点G到轨迹上端拐点A的直线段距离LAG，应大于钵体高度(20 mm)以保证能够将钵苗完全取出；移栽静轨迹环扣宽度即取秧点G到轨迹上B点的距离LBG，应大于钵体上端宽度W(W=18 mm)，以保证秧针能夹取到秧苗。

(2)取秧点G到钵体中心的距离为W/3～W/2，保证一次只取一个钵里的秧苗。

(3)取秧角(在取秧位置，秧针与水平线的夹角)在5°～12°之间，防止秧针靠近秧苗时戳伤秧苗枝叶。

(4)推秧位置C点位于移栽臂秧针尖点A′从A点间歇运动转过θ4(θ4=α-Δ，α为太阳轮无齿部分圆心角，Δ取5°～8°)后所在的位置，推秧角(在推秧时位置，秧针与水平线的夹角)在55°～65°之间。

(5)秧箱倾角一般在50°左右，移栽臂推秧角与取秧角的角度差应在45°～55°，保证秧苗插入土中的直立度。

(6)移栽静轨迹的高度为静轨迹的最高点到最低点的距离，应大于260 mm[23]。

(7)在推秧完成后，移栽臂回程时，移栽臂秧针动轨迹越过秧苗的高度L′>80 mm，否则认为动轨迹前倾，秧针回程时会推倒已种植好的秧苗(秧苗高度约为80 mm)。

表1 设计要求

2.2 正向设计

正向设计由多个步骤组成：①构造一个非圆齿轮节曲线方程，该方程可以是椭圆方程、偏心圆方程或是自主开发的特殊方程。②根据齿轮啮合过程的数值关系，利用数学建模的理论建立运动学模型，然后确定设计参数、设计目标和约束条件。③开发正向设计的参数优化软件。齿轮节曲线方程的参数、移栽机构安装角、移栽臂相关参数及株距作为输入量，在优化软件界面直观显示移栽机构工作轨迹、移栽臂姿态(取秧角、推秧角)及环扣尺寸，通过人机交互方式，优化得到移栽臂姿态满足取秧和推秧要求的移栽静轨迹。

前期已经开展了正向设计研究[14]，当株距为200 mm、双移栽臂移栽速度为200株/min时，正向设计得到的移栽静轨迹、动轨迹(其中一个移栽臂)如图4所示，正向设计得到的移栽机构轨迹存在不足之处：L′=39.8 mm，小于80 mm，故其动轨迹前倾明显，移栽臂秧针容易推倒已栽植好的秧苗。在此研究基础上，局部调整移栽静轨迹回程段，开展局部轨迹微调的反求设计。

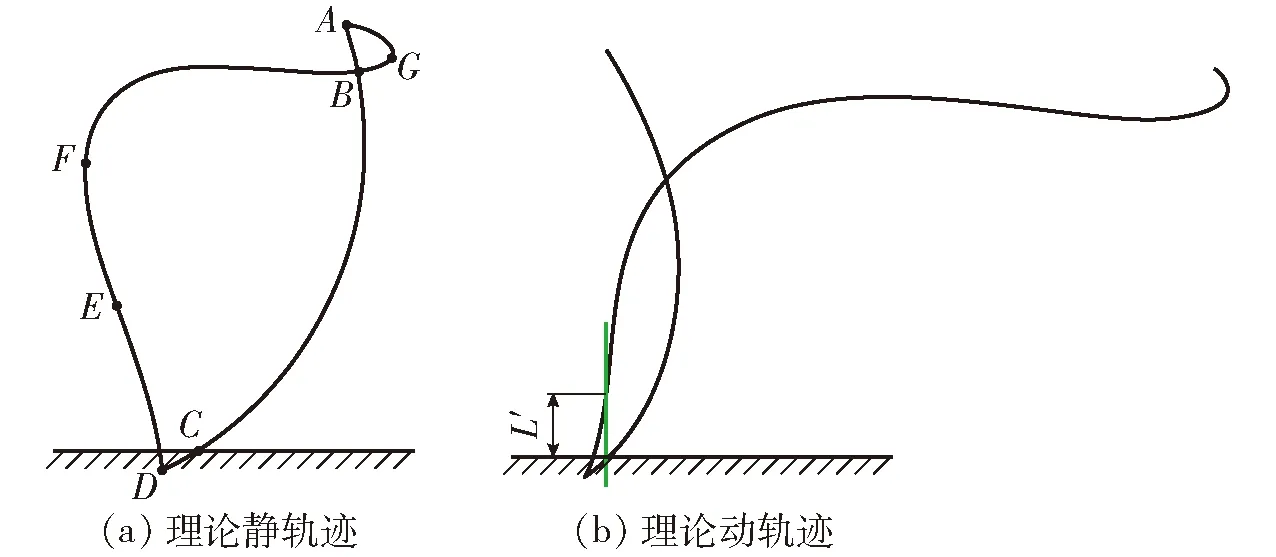
图4 “正向设计”的移栽轨迹

2.3 反求设计

反求设计是在正向设计基础上开展：①保持EFGA段轨迹和ABCD段轨迹不变，将移栽臂回程段DEF调整至DE′F，得到新的水稻钵苗移栽机构移栽静轨迹ABCDE′FGA，使得动轨迹满足设计要求，如图5所示；由于ABCD段轨迹为行星齿轮系间歇运动阶段，此时中间非圆齿轮和行星非圆齿轮都相对行星架保持静止，所以ABCD段轨迹是一段以行星架旋转中心为圆心，行星非圆齿轮旋转中心和移栽臂秧针尖点之间的距离为半径的圆弧，所以根据DE′FGA这段轨迹进行局部反求设计，图5中曲线1为调整后移栽静轨迹图。②在新的移栽静轨迹上选取25个数据点(型值点)(图6)，q0为轨迹起始点，即A点，q3位于G点位置，q14位于F点位置，q0到q14保证FGA段轨迹形状不被调整；q24位于D点位置，q14到q24根据要求往左侧调整(即DE′F轨迹段)，利用三次B样条曲线拟合型值点。③根据拟合调整后轨迹的型值点得到的数据求解移栽机构中非圆齿轮传动的总传动比，再分配两级齿轮传动比。④根据齿轮啮合关系确定非圆齿轮节曲线，建立移栽机构运动学模型，开发可视化辅助设计软件，可直观地表示机构的工作轨迹与姿态，以及各数值化的设计目标。

图5 移栽静轨迹

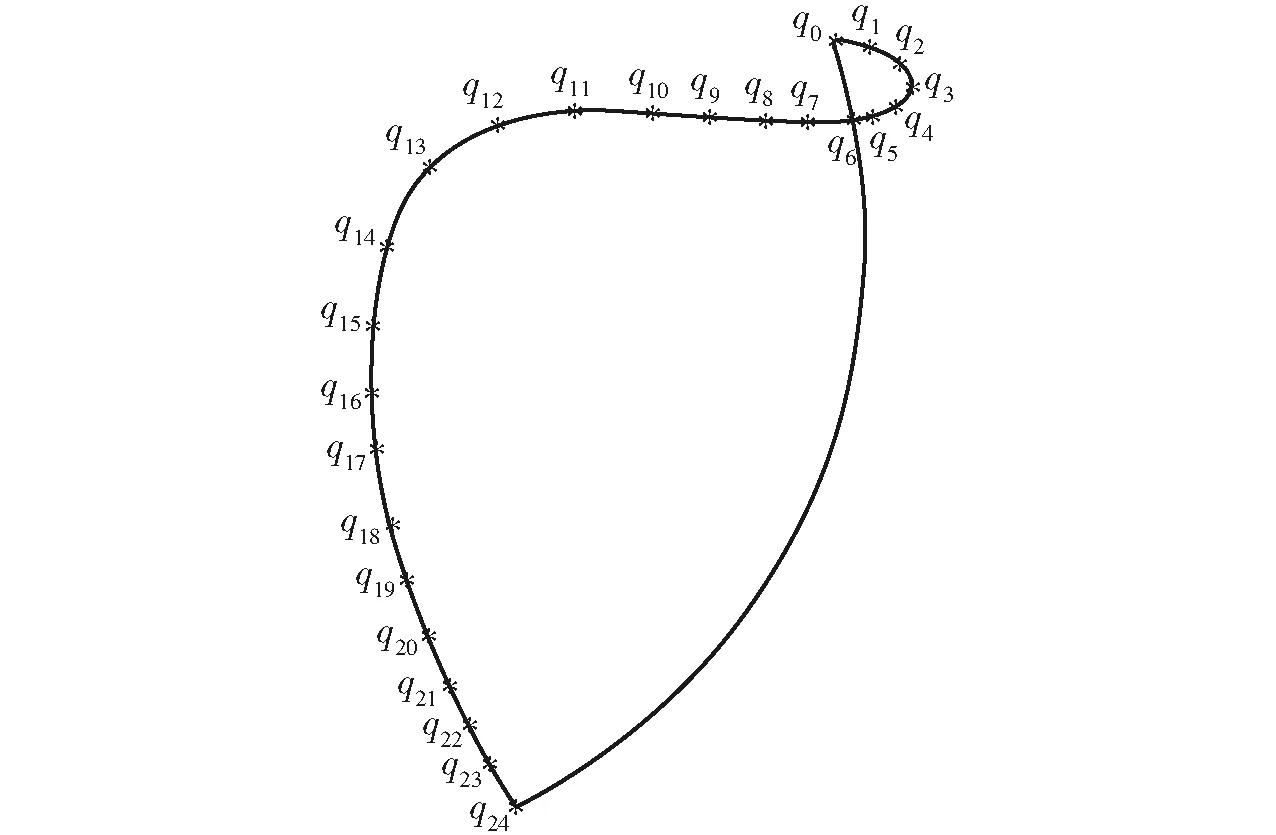
图6 调整后的移栽静轨迹型值点

以O点为原点、水平方向为x轴，垂直方向为y轴建立坐标系，移栽机构单臂初始位置如图7a所示。将移栽机构模型转化为平面RR杆开链机构模型，该机构有固定的旋转铰链O，OI为曲柄，IA′为摆杆，如图7b所示。规定曲柄OI的角位移φ5是从OI到x轴的角度，摆杆相对于曲柄的角位移φ7是从OI到IA′的角度，φ6是从OA′到OI的角度，φ4是从OA′到x轴的角度。当曲柄和摆杆按照一定规律的φ5和φ7运动就可以实现移栽臂秧针尖点A′按调整后的轨迹曲线1(图5所示)的DE′FGA轨迹段运动。

图7 移栽机构简图

由于移栽静轨迹回程最左侧轨迹线位于行星架回转中心位置右侧，因此，L2>L1，反求设计具体计算步骤如下：

(1)

式中L3——行星架回转中心O到移栽臂秧针尖点A′的距离，mm

xA′、yA′——利用B样条曲线插值拟合q0到q24型值点得到的轨迹数据点坐标，mm

(2)

(3)

式中L1——行星架回转中心O到行星非圆齿轮回转中心I距离，mm

L2——行星非圆齿轮回转中心I到移栽臂秧针尖点A′的距离，mm

由于太阳轮为不完全非圆齿轮，计算齿轮节曲线时，令行星架旋转方向与实际相反即取逆时针，角度以逆时针为正。故计算时，秧针尖点A′在不同位置的坐标值为轨迹上对应数据点的坐标，即依次取从q0点到q24之间的插值拟合产生的数据点坐标值。秧针尖点A′在q3处时L3最大，即maxL3，秧针尖点A′在q14处时L3最小，即minL3。因此，保持FGA段轨迹不变即maxL3和minL3不变，由式(2)、(3)可得L1和L2不变，从而确保在取秧位置G点处取秧角不变；由于在ABCD段轨迹阶段，移栽臂相对行星架不转动，因此保持ABCD段轨迹不变确保了到达推秧位置C点处推秧角不变，故理论上保证了取秧姿态和推秧姿态不变。

移栽机构运动过程中，φ4、φ5及φ6满足关系

φ5=φ6-φ4

(4)

其中

φ4=arctan(yA′/xA′)

(5)

当秧针尖点A′在DE′FGA段轨迹不同位置时，依次取从点q0到q24之间的插值拟合产生的数据点坐标值，则φ6和φ7数值关系如下(以q3、q14为分界点)：当秧针尖点A′在点q0(包含点q0)到点q3之间时，有

当秧针尖点A′在点q3时，有

φ6=0φ7=π

当秧针尖点A′在点q3到q14之间时，有

当秧针尖点A′在点q14时，有

φ6=πφ7=2π

当秧针尖点A′在点q14到q24(包含点q24)之间时，有

其中秧针尖点A′在点q0和点q24两位置时L3相等。

移栽机构总传动比初值为

(6)

参考圆柱齿轮等效转动惯量最小原则条件和二级齿轮传动系统传动比分配方法，构建第二级齿轮传动比初值

(7)

由于第二级齿轮传动为行星非圆齿轮和第二中间非圆齿轮啮合组成，则行星非圆齿轮节曲线向径R4和第二中间非圆齿轮节曲线向径R3为

R4=a2i20/(1+i20)

(8)

R3=a2-R4

(9)

式中a2——第二级啮合齿轮中心距，mm

根据非圆齿轮啮合原理，行星非圆齿轮旋转过的弧长与第二中间非圆齿轮的弧长相等，即

R3dφ2=R4dφ7

(10)

式中φ2——第二中间非圆齿轮相对行星架的角位移，rad

行星非圆齿轮旋转360°时，第二中间非圆齿轮也旋转360°，可得

(11)

参考正向设计得到的第二级齿轮中心距数值，取反求设计中第二级齿轮中心距初值为a20，则行星非圆齿轮的节曲线向径R4取a20/(1+i20)，代入式(11)进行迭代搜索，若φ2小于2π则中心距a2等于a20加一个步长，重新代入式(11)迭代计算直到φ2与2π差值在精度(精度为0.01 mm)要求内，算出第二中间非圆齿轮与行星非圆齿轮中心距的精确值a′2，那么第二中间非圆齿轮节曲线向径的精确值R′3为

R′3=a′2-R4

(12)

第二级非圆齿轮副传动比的精确值为

(13)

第一级齿轮传动比初值为

(14)

同理，给定第一中间非圆齿轮与太阳轮(不完全非圆齿轮)的中心距初值a10，再根据节曲线封闭条件和啮合条件，采用迭代搜索获得中心距a1的精确值。

R2=a1i10/(1+i10)

(15)

R1=a1-R2

(16)

式中a1——第一级啮合齿轮中心距，mm

R1——太阳轮节曲线向径，mm

R2——第一中间非圆齿轮节曲线向径，mm

根据非圆齿轮啮合原理，第一中间非圆齿轮旋转过的弧长与太阳轮的弧长相等，即

R1dφ1=R2dφ2

(17)

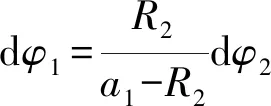
(18)

第一中间非圆齿轮旋转360°时，太阳轮旋转2π-α，可得

(19)

式中φ1——行星架相对太阳轮的转角，rad

α——太阳轮无齿部分的圆心角，rad

参考正向设计得到的第一级齿轮中心距数值，取反求设计中第一级齿轮中心距初值为a10，则第二中间非圆齿轮向径的精确值R2为a10/(1+i10)，代入式(19)进行迭代搜索，若φ1小于2π-α，则中心距a1等于a10加一个步长，重新代入式(19)迭代计算直到φ1与2π-α差值在精度要求内，搜索算出第一级非圆齿轮副中心距的精确值a′1，那么太阳轮向径的精确值R′1为

R′1=a′1-R2

(20)

第一级非圆齿轮副传动比的精确值为

(21)

移栽臂的秧针尖点A′位移方程，即静轨迹曲线的方程为

(22)

(23)

(24)

其中

xI=L1cosφ5yI=L1sinφ5

式中β——OI和OH的夹角，rad

φ3——行星非圆齿轮相对行星架角位移，rad

当株距为H时，移栽臂的秧针尖点A′的动轨迹曲线方程为

(25)

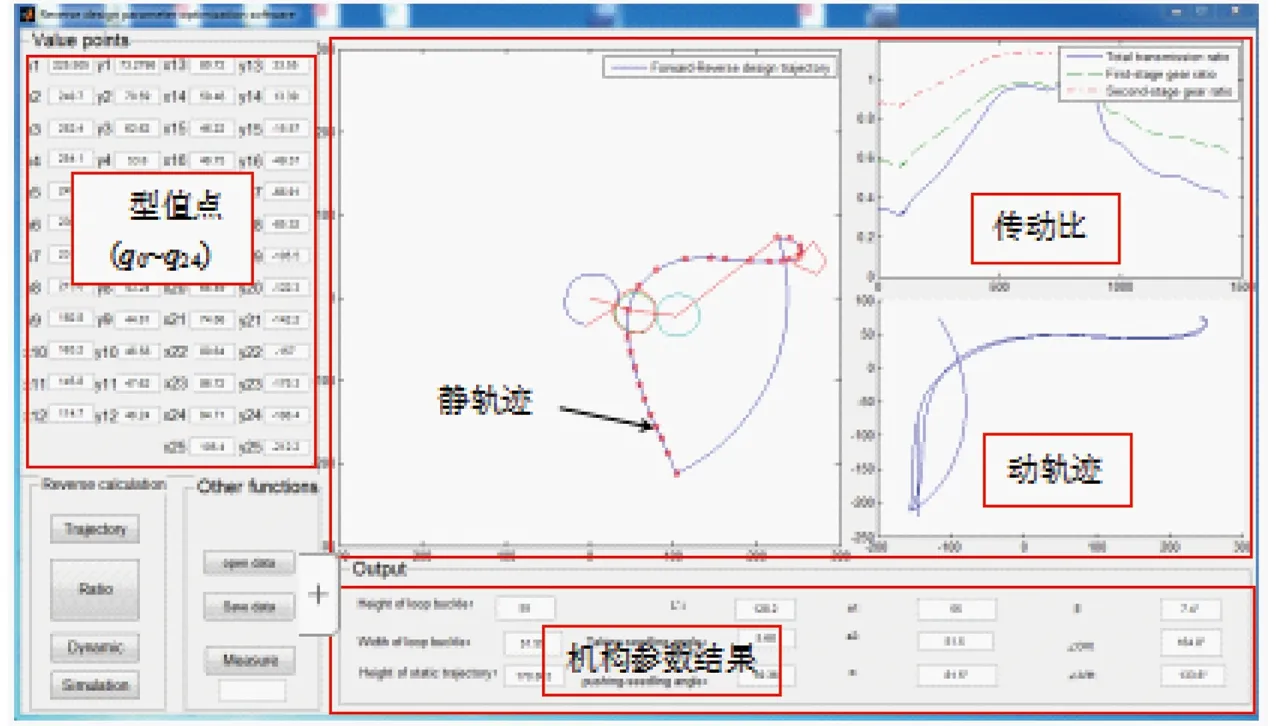
图8 反求设计的辅助设计软件界面

基于Matlab平台，自主开发反求设计的辅助设计软件，其主界面见图8。在该软件上可以实现如下功能：可以输入25个型值点的x和y坐标数据，直观显示静轨迹、动轨迹、传动比曲线和移栽机构，输出机构参数、取秧角、推秧角、推秧角和取秧角的角度差、轨迹高度、环扣尺寸及秧针动轨迹越过秧苗的高度L′等参数。在正向设计得到的移栽静轨迹上选择25个数据点(即q0～q24)，不断调整数据点q15～q24数值，观察移栽静轨迹、动轨迹和秧针动轨迹越过秧苗的高度L′，直到L′满足设计要求，最终获得满足移栽轨迹和姿态要求的移栽机构结构参数。

2.4 设计结果

利用反求设计的辅助设计软件得到移栽机构的各齿轮节曲线数据点(齿轮节曲线数据点导入齿廓生成软件中获得齿廓数据点用于三维建模)及齿轮相对位置等参数(即a′1=55 mm,a′2=51.6 mm,α=81.5°,β=7.4°)。最终设计数据点q0～q24的x、y坐标如表2所示，正反求设计方法设计得到的参数结果如表3所示。

表2 q0～q24的x、y坐标

表3 正反求设计方法结果与正向设计、设计要求比较

从表3和图9可知，正反求设计方法得到移栽臂秧针尖点动轨迹越过秧苗根部的高度L′等于128.2 mm，远大于80 mm，改善了正向设计时的动轨迹，提高了秧苗植苗率和直立度，同时保持了正向设计时得到的取秧姿态、推秧姿态及环扣尺寸，满足设计要求。综上所述，正反求设计方法设计得到的移栽机构在理论上不仅满足移栽姿态的要求，同时满足移栽轨迹的要求，解决了过去单一的正向设计或反求设计存在不能同时具备良好的移栽姿态和轨迹的问题。

3 运动学仿真与样机试验

3.1 机构设计与运动学仿真

图9 正反求设计方法得到的移栽轨迹

根据正反求设计方法得到满足设计要求的移栽机构各个齿轮节曲线和齿轮相对位置的参数，结合这些数据对移栽机构进行结构设计；将各个齿轮节曲线数据导入自主开发的齿廓生成软件[24-27](如图10)，给定齿轮的齿数，得到各非圆齿轮的齿廓线数据，运用三维建模软件Pro/E 5.0对该机构各个零件进行三维实体建模和虚拟样机装配，最后在ADAMS软件中完成虚拟样机仿真试验，生成仿真静轨迹、动轨迹曲线以及移栽臂秧针尖点坐标数值，虚拟仿真移栽静轨迹数据导入AutoCAD软件测得添加缓冲装置后移栽静轨迹高度。将理论计算静轨迹、动轨迹分别导入ADAMS，轨迹对比如图11所示，虚拟仿真得到的轨迹与理论计算得到的轨迹基本重合，唯一不同的是虚拟仿真得到的轨迹下端是圆弧，理论计算得到的轨迹下端为尖点，其原因是结构设计时考虑不完全齿轮冲击问题，机构添加了缓冲装置，而理论计算时未考虑缓冲装置。由于结构设计过程中，行星架的回转中心与地面的距离不变，因此轨迹下端因缓冲装置变成圆弧对回程段秧针动轨迹越过秧苗根部的高度L′不影响。

图10 齿廓生成软件界面

图11 虚拟仿真与理论计算轨迹对比

3.2 样机试验

为了验证正反求设计方法研究的正确性和可行性，研制移栽机构物理样机并安装在土槽试验台上完成高速摄像运动学试验。利用高速摄像机捕获移栽机构一个工作周期内的运动过程，将拍摄帧速率设置为300 f/s，移栽机构的转速为100 r/min，使用Blaster’MAS图像分析软件获得试验静轨迹(如图12所示)，分析记录移栽机构齿轮箱每转10°移栽臂秧针尖点的坐标数值。使用DMI410型数显倾角仪测量移栽臂在取秧和推秧位置上的取秧角和推秧角度。

3.3 结果分析

通过对比理论计算、虚拟仿真、样机试验测量的结果，并将相应参数与水稻钵苗移栽机构设计要求逐一进行对比，可以看出：

(1)如图11所示，比较理论计算、虚拟仿真得到的移栽静轨迹和动轨迹，结果表明静轨迹基本吻合。比较图11、12可知，样机试验得到的静轨迹形状与理论计算和虚拟仿真得到的基本一致。此外，如图13所示，虚拟仿真和样机试验的秧针尖点不同位置对应静坐标基本一致，由式(25)可知，当移栽株距、移栽机构旋转速度相同，样机的动轨迹与虚拟仿真的动轨迹基本一致。虚拟仿真移栽动轨迹数据导入AutoCAD软件测得秧针动轨迹越过秧苗根部高度L′为127.8 mm，满足设计要求。

图12 台架试验和试验测试轨迹

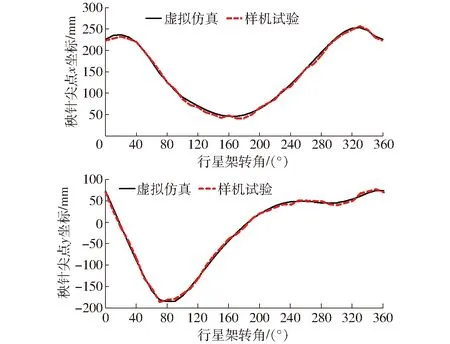
图13 秧针尖点坐标曲线

(2)由表4可知，移栽机构的移栽静轨迹环扣高度和宽度、轨迹高度、取秧姿态、推秧姿态误差都不大于3.17%，故均满足设计要求。

上述表明：移栽静轨迹、动轨迹的参数及移栽姿态均满足设计要求，验证了正反求设计方法的正确性和可行性。

表4 理论计算、虚拟仿真、试验测试及设计要求比较

4 结论

(1)分析了现有旋转式移栽机构设计方法的特点，提出了一种基于人机交互的正向设计与局部轨迹微调的反求设计相结合的正反求设计方法。

(2)建立了旋转式移栽机构反求设计数学模型，并开发了反求设计的辅助设计软件，最终得到移栽机构的机构参数。该移栽机构同时满足移栽要求的移栽轨迹和姿态，其推秧角达到59.72°，推秧角与取秧角的角度差为53.86°，移栽臂秧针尖点动轨迹越过秧苗根部的理论高度为128.2 mm，远大于80 mm的设计要求。

(3)利用Pro/E 5.0完成非圆齿轮行星轮系水稻钵苗移栽机构的三维建模、装配，并在ADAMS软件中进行虚拟仿真分析，同时将该机构安装在试验台上，完成高速摄像运动学试验，将实际测试的移栽静轨迹与理论计算、虚拟仿真得到的静轨迹进行对比，同时将移栽机构相应目标参数与设计要求逐一对比，验证了正反求设计方法的正确性和可行性。