分级循环荷载下泥岩的非线性特征参数试验∗

陈钒，潘旦光，王轲，鲁文艳，李冬晴

(1.北京科技大学土木工程系，北京100083；2.中电建路桥集团有限公司，北京100048；3.同济大学土木工程防灾国家重点实验室，上海200092)

随着经济的发展与社会的需求，大跨度桥梁、水利水电工程、超长隧道等大型工程越来越多，这些工程很多修建于稳定性更好的岩石类场地.在地震荷载、冲击荷载等动力荷载作用下，岩石的材料属性与常规荷载作用下的属性截然不同.在地震工程领域，一般只考虑土体的非线性特征，而将岩石视为完全刚性体或弹性体.这对于强度高的硬岩是合适的，但对于泥岩、粉砂岩等软岩，在强震作用下易产生塑性变形，伍法权等[1]认为在一定埋深下的软岩大变形还表现出强烈的非线性，因此确定泥岩等软岩在地震作用下的变形特性及强度特性尤为重要.

对于工程岩体，一些学者通过循环加载的方式研究岩石的强度、变形、动力参数等.林卓英等[2]研究表明岩石在循环荷载作用下的强度低于其单轴强度，并认为引起疲劳破坏的根本原因就是塑性变形的积累；李愿军[3]通过岩石动力学试验给出了凝灰岩、凝灰质砂岩、霏细斑岩、流纹斑岩的动态弹性模量、泊松比等；Nishi K等[4]通过循环荷载试验得到了岩石的阻尼参数，探讨了阻尼特性；朱明礼、朱珍德等[5,6]研究了不同频率下花岗岩动应变应力滞回曲线、动弹性模量和阻尼比同动弹性模量及循环频率之间的关系；刘建锋等[7,8]通过试验研究了阻尼参数与循环荷载周次及幅值动应力的相关关系，认为低周循环荷载试验的中间周次滞回环得到的阻尼参数可表征岩石的阻尼特征；何明明等[9,10]研究了不同循环加载条件下岩石的阻尼特性，揭示了常幅循环荷载下阻尼比和阻尼系数随循环次数的演化规律；苏鹏[11]通过试验得到了砂岩与花岗岩的阻尼比与振动频率、应力水平、应变幅值的关系.

对于理想黏弹性体，在循环荷载的条件下，由于黏滞力的存在，各级循环中应变相位滞后于应力相位，滞回环应为标准的椭圆形，且由于没有塑性变形，不同应力幅之间的滞回环的应变起点应位于同一应变位置.但由于岩石内部存在一定的微裂隙、微孔洞等微结构特征，实际上为非理想弹性体.Tutuncu A N 等[12,13]提出应力应变滞回曲线的形状与加载频率、应变振幅等因素有关；陈运平等[14]认为岩石的滞回环主要有椭圆形、新月形、尖叶形，并指出在加载阶段应变的相位可能超前、同步或落后于应力的相位，而在卸载阶段应变总是落后于应力相位；Mckavanagh B等[15]提出滞回环形状与应变之间的近似关系，当岩石应变振辐为10−5∼10−3（中等应变）时，滞回环出现了尖点，当应变振幅为10−6及以下（小应变）时滞回环为椭圆形；肖建清等[16]认为若加载段中应变相位超前于应力相位，则呈新月形；若既有滞后又有超前，则呈长茄形，并给出应变现象超前于应力现象的原因；蒋新兴等[17]通过对细砂岩做单轴循环加载试验，认为随着振幅的增大滞回环的面积也增大，能量缺失越多，阻尼比增大；刘建锋等[18]认为应变相位始终滞后于应力相位，滞回环在荷载反转处是尖叶形，并非椭圆形.

以上研究对岩石的动力特性进行了一定探讨，但对于循环荷载作用下岩石的变形特性、阻尼特性及强度特性随循环次数与动应力幅值的变化规律并没有深入研究.为此，通过变幅分级循环加载试验研究泥岩的滞回曲线特性，循环荷载次数与不同动应力幅值对泥岩阻尼比、动弹性模量的变化规律的影响，试验成果可用于泥岩场地地震反应分析.

1 试验概述

1.1 试样及试验设备

试验所用岩石为泥岩试样，泥岩取自重庆市江习高速笋溪河特大桥场地南侧，地表下100 m∼200 m处.该场地地下水静止水位为地表下10.5 m，深部基岩裂隙水较发育，现场钻孔取出岩芯后立即进行密封，以保持其原始状态.根据《水利水电工程岩石试验规程》[19]的制样要求，试样尺寸为φ50 mm×100 mm，端面平行度在±0.02 mm以内，加工后的试样如图1所示.

图1 泥岩试样Fig 1 Mudstone sample

图2 单轴试验全应力应变曲线Fig 2 Uniaxial test full stress-strain curve

1.2 试验方案

在进行分级循环加载之前，首先进行单轴抗压强度试验，以确定循环荷载分级.典型的单轴试验全应力应变曲线如图2所示.

根据单轴压缩试验的结果，可知泥岩的抗压强度为7.5 MPa∼12.6 MPa，平均值为9.5 MPa.为保证在低应力水平下有足够的试验数据，变幅分级循环加载的各级动应力增量在加载初始阶段（前9级）取1 MPa，后期（第10级之后）取3 MPa，直至试样发生破坏.加载波形为正弦波，每级荷载循环40次，加载频率为1 Hz，由试样原位深度取试验围压为2.5 MPa.定义σmin、σmax分别为各级加载的最小、最大动应力，Pmin、Pmax分别为对应的最小、最大动荷载，∆σ=σmax−σmin为应力增幅，加载方案如表1所示.

表1 动应力分级加载表Tab 1 Dynamic stress loading schedule

1.3 试验原理

对于理想弹性体，在动应力的作用下，动应力和动应变与时间的波形线必然在时间上是同步对应的.对于非理想弹性体，其动应力σd与动应变εd的波形线在时间上并不完全对应，两者之间恒有一定的时间差，这使同一振动周次的动应力和动应变曲线形成滞回环，典型的滞回环如图3所示，其中BE线的值由该次循环下的动应力幅值确定，即σBE=(σmax+σmin)/2.

滞回环面积的大小反映了在加卸载过程中能量损失的大小，这部分能量损失由阻尼比λ表示；滞回环的平均斜率反映了本次循环下动弹性模量Ed的大小.根据《地基动力特性测试规范》[20]，阻尼比λ与动弹性模量Ed的计算公式为：

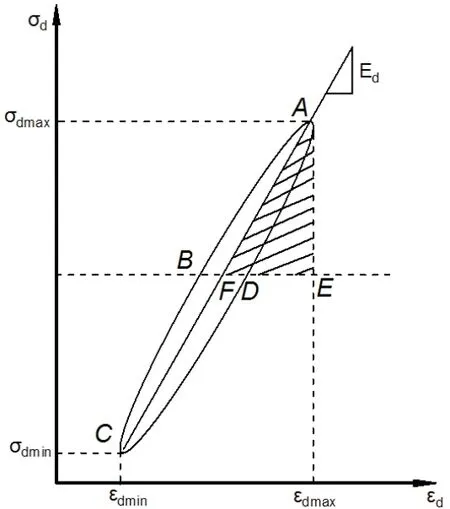
图3 动应力-动应变滞回环Fig 3 Dynamic stress-dynamic strain hysteresis loop

式中：AR为滞回环ABCD的面积，由滞回环终止点与初始点相连而形成闭合条件；As为三角形AFE的面积.在数据处理时，滞回环面积采用微元法求解梯形面积叠加进行计算.σdmax、σdmin、εdmax、εdmin分别为动应力与动应变的最大最小值.

2 滞回环的特性

图4为各级加载下第21次循环的滞回环，图4(a)为前五级加载下的滞回环，图4(b)为第6∼11级加载下的滞回环.

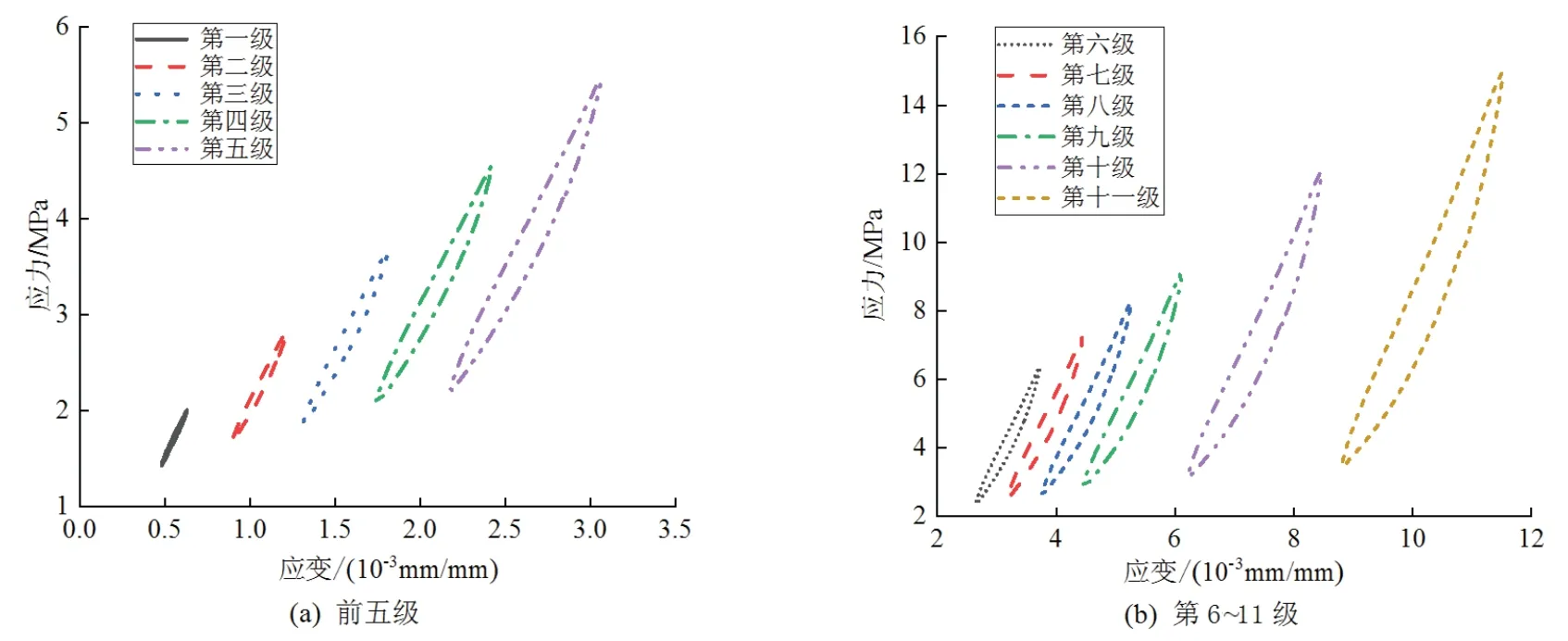
图4 各级加载下第21次循环滞回环Fig 4 21st cycle hysteresis loop per loading

由图4可看出，在不同循环荷载的加载下，各滞回环的最小应变值并不是在同一点，而是随着荷载级数的增大，各滞回环最小应变值也逐级增大.这说明在每一级循环加载过程中都会产生一定的塑性变形，相邻滞回环间的最小应变差可视为在一级加载中引起的总的塑性应变值.由图4(a)可知，在前五级加载下，应变振幅小于3×10−3，各滞回环形状近似于尖叶形；由图4(b)可知，当应变振幅超过这一值时，滞回环整体形状与前五级相比发生了改变，变为了柳叶形，这说明随着荷载级数的增大，滞回环形状会发生改变.但在荷载反转处，各级荷载下的滞回环都为尖叶状，而不是表征线性黏弹性的椭圆状，这是因为加载过程中应变振幅的数量级都为10−3，远大于10−6，不属于小应变阶段，泥岩内部出现了微塑性，此时已不能用线性黏弹性来表征泥岩变形机制，而应是非线性衰减机制.尖叶状说明在荷载反转时，泥岩的弹性变形迅速响应，即在荷载反转时产生的塑性变形较小，因此可认为循环加载过程中产生的塑性变形并不是在荷载反转时产生.

为了进一步研究加卸载过程中的应力应变滞后关系，分别取第3级与第10级荷载下的第20、21、22次循环，应用公式(3)对应力应变进行归一化，归一化后绘出应力-时间与应变-时间曲线如图5所示.

在再生混凝土中适量掺入钢纤维，可以增强其抗拉、抗折、抗弯和抗剪等性能。由于直接进行混凝土的轴心抗拉试验很繁琐，因此大多数的研究是采用劈裂抗拉试验取代轴心抗拉试验。由于现行的钢纤维再生混凝土(Steel Fiber Recycled Aggregate Concrete，SFRAC)试验方法仍沿用劈裂抗拉强度来确定轴心抗拉强度，但并未说明如何将劈裂抗拉强度换算成钢纤维再生混凝土的轴心抗拉强度。因此，本文设计了一种新型的钢纤维再生混凝土轴心抗拉试件——哑铃型试件，在普通试验机上获得混凝土的轴心抗拉强度[4]。

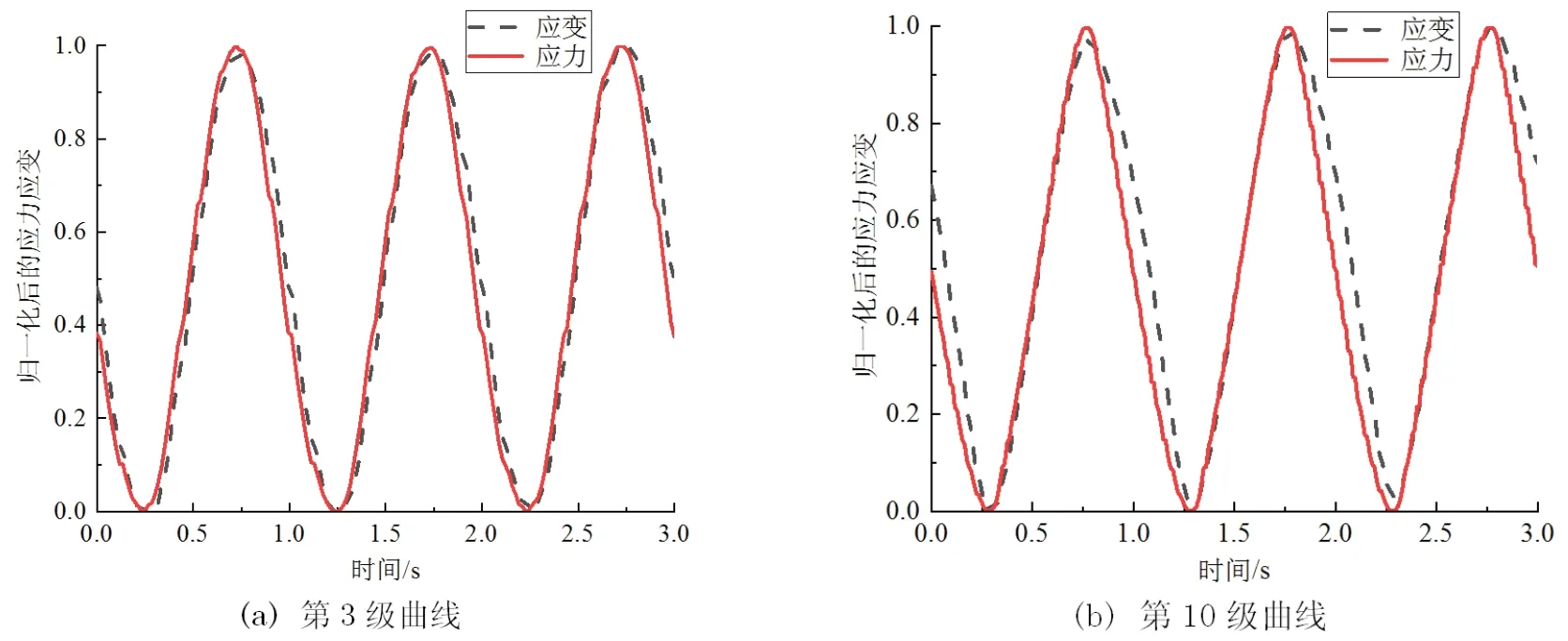
图5 第3、10级荷载下的应力-时间与应变-时间曲线Fig 5 Stress-time and strain-time curve at 3rd and 10th loads

式中：Ai为应力、应变的原始数据，为归一化后得到的应力、应变数据.

由图5可知，在加载过程中，第3级荷载的应力相位稍微超前于应变相位，第10级荷载的应力相位几乎与应变相位同步，这说明在第3级加载时泥岩内部仍有部分微裂隙，处于孔隙裂隙压密阶段；而第10级加载阶段的应力应变关系几乎处于弹性阶段，因此图4中第10级滞回环的加载阶段更接近于直线.由常规单轴试验的全应力应变曲线图2，泥岩在应变小于2×10−3时处于孔隙裂隙压密阶段，应变超过10−2时进入非稳定破裂发展阶段，应变为1.24×10−2时达到峰值强度并发生破坏.在试验中，由各级加载的滞回环形状，前5 级加载阶段滞回环形状都上凸，即应变都滞后于应力，可视为处于孔隙裂隙压密阶段；第6∼11级加载阶段滞回环形状接近直线，即应变同步于应力，可视为处于弹性变形阶段.这说明进行分级循环加载泥岩较难进入弹性阶段，进入弹性阶段后会持续较长时间，且破坏前并不会产生非稳定破裂发展阶段.因此循环加载中泥岩破坏时的强度并没有达到峰值强度，而是发生了疲劳破坏.

在图5曲线的波峰、波谷，即荷载反转处，应变相位都滞后于应力相位，但滞后量较小，弹性应变响应迅速，因此在荷载反转处产生的塑性变形较小，这与上述分析一致.在卸载阶段，尤其是第10级曲线，应变相位大幅滞后于应力相位，这种现象是由两个原因引起的，一是由于泥岩内部存在的微裂隙、液体等引起的泥岩黏弹性特性，从而导致弹性变形滞后恢复而引起应变滞后于应力，二是由于塑性变形的产生引起应变滞后于应力.在双重效应下，反映在滞回环上即为第10级滞回环的卸载阶段下凹严重.

由以上分析，可知泥岩应力应变滞后关系可反映滞回环的形状.加载阶段若应变滞后于应力，滞回环形状为上凸；若应变同步于应力，滞回环形状为直线；若应变超前于应力，滞回环形状为上凹.卸载阶段若应变滞后于应力，滞回环形状为下凸.应力应变滞后关系主要与泥岩的黏弹性特性、塑性变形及压密的难易程度有关，其中泥岩的黏弹性特性以及压密的难易程度取决于泥岩内部本身存在的微裂隙、微孔洞及含水量等.

3 泥岩阻尼比变化规律

在分级循环加载试验下泥岩的总应力应变曲线如图6所示，可知试样在第12级加载时发生破坏，破坏时最大应力为16.87 Mpa.

图6 总应力-应变曲线Fig 6 Total stress-strain curve

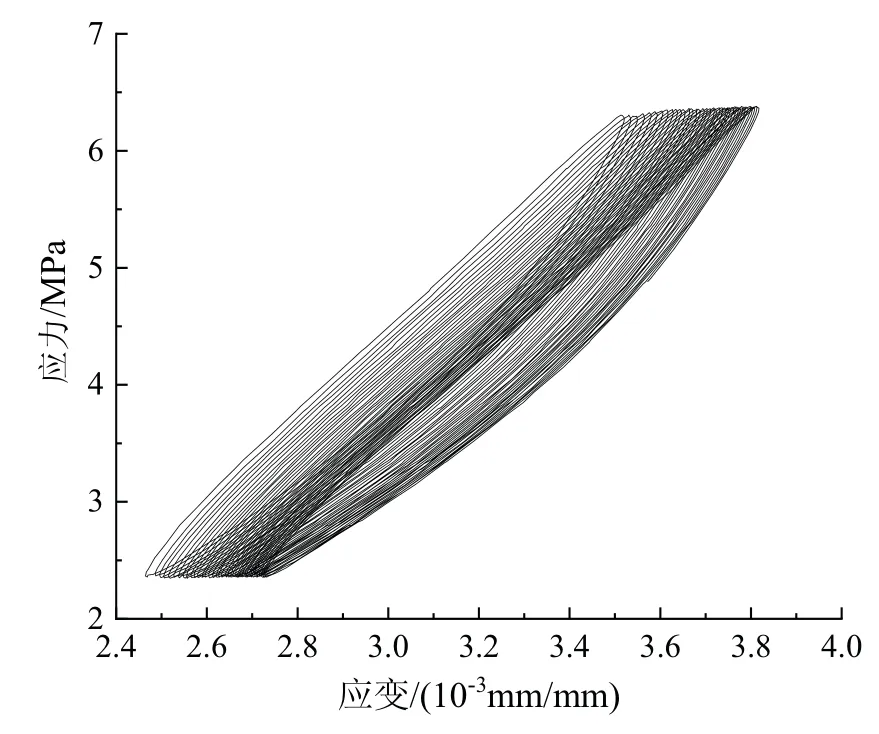
图7 第6级荷载作用下应力-应变关系曲线Fig 7 Stress-strain relationship curve under the 6th stage load

取任意一级荷载作用下测得的应力应变关系，即为常幅循环加载下的试验结果.以第6级荷载为例，可绘出该级荷载作用下的应力应变曲线如图7所示.

由图7可看出，在常幅循环荷载作用下，滞回环逐渐向应变增大的方向发展，且滞回环形状越来越闭合，面积越来越小，这说明在动应力幅值不变时，随着循环次数的增大，累积塑性变形增大，但产生塑性变形的速率降低.根据公式(1)，可计算出各级荷载作用下各次循环下的阻尼比，如图8所示.

由图8可以看出，由于第1级加载泥岩内部微孔隙裂隙刚开始压密闭合，且第1级轴向荷载较小，试验机较难控制精度，因此第1级阻尼比离散性较大，从第2级开始曲线逐渐光滑.在泥岩破坏前阶段，即前11级加载中，随着循环次数的增多，每一级阻尼比都会逐步减小并收敛于一个定值.阻尼比反映了该次循环荷载的耗能能力，阻尼比随着循环次数增加而稳定说明在常幅加载下，当循环次数足够多时，滞回环面积逐渐相等，泥岩内部微裂隙的产生速度降低，已不再产生新的塑性变形，这与图7的应力应变曲线吻合.本试验循环40次，得到的阻尼比可以作为该级荷载作用下的极限阻尼比.

在前3级荷载的作用下，随着循环次数增大，同级的阻尼比曲线下降趋势明显；在4∼11级荷载的作用下，同级的阻尼比曲线变化不大，下降趋势不明显.可认为在低应力的情况下，由循环次数引起的阻尼比变化较大；高应力情况下，由循环次数引起的阻尼比变化不大.而第12级荷载作用下阻尼比随循环次数增加明显增大，这是由于泥岩内部裂纹已经贯穿，能量大量耗散，试样发生了破坏.

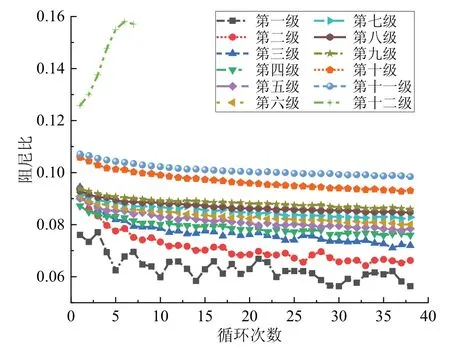
图8 各级荷载阻尼比与循环次数关系Fig 8 Relationship between damping ratio and cycle number under different loads

随着加载级数的增加，即随着动应力幅值的增加，阻尼比曲线逐级增加上移.可认为随着应力幅值增加，泥岩内部由应力引起的裂纹、裂隙越来越发展，颗粒之间内摩擦增大，由此引起的能量耗散越来越大，造成阻尼比越来越大，直至试样发生破坏.

4 泥岩动弹性模量变化规律

根据公式(2)，可计算出各级荷载作用下各次循环下的动弹性模量.各级荷载作用下各次循环下的动弹性模量如图9所示.

由图9可以看出，在前10级加载中，当动应力幅值不变时，随着循环次数的增多，各级动弹性模量会逐步增大并收敛于一个定值，这说明同级滞回环的加卸载曲线斜率逐渐增大并趋于稳定，泥岩动弹性模量逐渐增大.其中，在前3级荷载的作用下，随着循环次数增大，同级的动弹性模量曲线上升趋势明显；在3∼10级荷载的作用下，同级的动弹性模量曲线变化不大，上升趋势不明显.因此可认为，在低应力的情况下，由循环次数引起的动弹性模量变化较大；高应力情况下，由循环次数引起的动弹性模量变化不大.第11级荷载作用下动弹性模量随循环次数增加而不收敛于定值，第12级荷载作用下动弹性模量明显大幅下降，说明泥岩内裂纹已经贯穿，产生破裂面，发生破坏.即泥岩在破坏前动弹性模量一直增大，破坏时动弹性模量突然大幅下降.

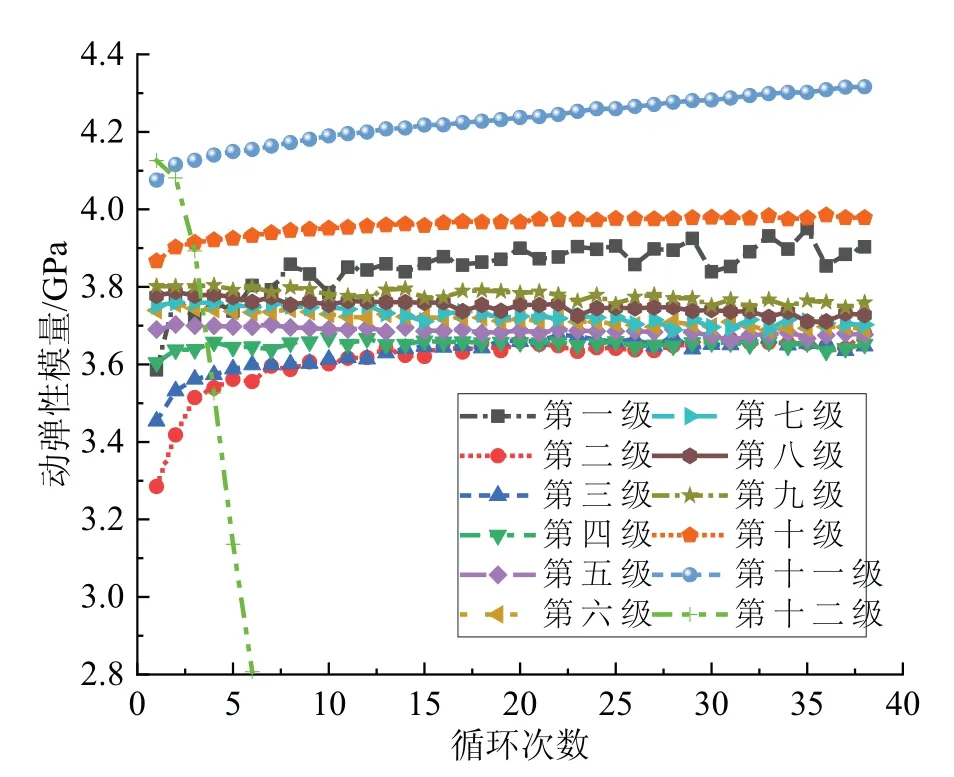
图9 各级荷载动弹性模量与循环次数关系Fig 9 Relationship between dynamic elastic modulus and cycle number under different loads

在第2∼11级荷载作用下，随着动应力幅值的增加，动弹性模量曲线也呈逐级增加上移的趋势，可认为随着动应力幅值的增加，泥岩动弹性模量越来越大.这表明泥岩内部孔隙裂隙虽然不断发展，但都处于压密的状态，其变形性质更接近于线弹性，且具有较大的动弹性模量.而多组试验结果表明，第1级荷载产生的动弹性模量总是较后面几级偏大，说明在循环加载的初始阶段，泥岩动弹性模量普遍较大.这是因为在初始加载阶段，泥岩内部裂隙的凸齿之间刚刚接触但并不发生破坏，因此凸齿之间的接触咬合会使泥岩动弹性模量较高.随着动应力幅值的增大，泥岩内部裂隙表面已经经过充分的扰动，裂隙中的凸齿部分已经被压碎，因此动弹性模量会较第1级荷载下变小.

5 结语

(1) 泥岩应力应变滞后关系可反映滞回环的形状.前5级荷载的加载阶段应变滞后于应力，加载阶段滞回环形状为上凸；第6∼11级荷载的加载阶段应变同步于应力，加载阶段滞回环形状为直线.卸载阶段应变都滞后于应力，卸载阶段滞回环形状为下凸.在荷载反转时泥岩弹性变形响应迅速，卸载阶段应变滞后于应力，这是由泥岩的黏弹性特性与塑性变形的产生共同引起的.

(2) 在常幅循环加载中，泥岩阻尼比随循环次数增大而逐步降低并收敛于一定值，这说明在动应力幅值不变时，随着循环次数的增大，累积塑性变形增大，但产生塑性变形的速率降低；泥岩动弹性模量随循环次数增大而逐步增大并收敛于定值，这说明同级滞回环的加卸载曲线斜率逐渐增大并趋于稳定，泥岩动弹性模量逐渐增大.

(3)在变幅分级循环加载中，阻尼比随着动应力幅值增大而增大；对于泥岩动弹性模量，除初始阶段外，随着动应力幅值的增大，泥岩动弹性模量逐步增加直至破坏.