一种机动目标运动要素估计算法

程 帅, 张秦南, 王立文

一种机动目标运动要素估计算法

程 帅, 张秦南, 王立文

(中国船舶重工集团公司 第705研究所, 陕西 西安, 710077)

对于机动目标的运动要素估计, 当前运用较多的是基于匀加速模型的卡尔曼滤波方法, 但由于卡尔曼滤波器本身的缺陷, 该方法只适用于目标做匀加速直线运动的情况, 而无法对目标做转弯运动时的运动要素进行有效估计。为了克服这个问题, 文中提出了一种机动目标运动要素的估计算法, 通过对卡尔曼滤波协方差阵的定期重置, 使得增益矩阵的绝对值始终保持在较大的状态, 对估计值的修正效果始终处于一个较好的水平, 最终解决包含转弯运动在内的机动目标运动要素的估计问题。数学仿真结果表明, 所设计的估计算法对机动目标具有较强的跟踪能力, 满足了估计误差要求, 该方法简单可行, 易于工程实现。

目标运动要素; 估计算法; 匀加速; 转弯运动; 卡尔曼滤波

0 引言

双层壳体潜艇的出现对轻型反潜鱼雷提出了新的要求。由于鱼雷装药量有限, 因此需要采用聚能爆破战斗部和垂直命中技术来提高鱼雷的毁伤效果[1]。快速准确地估计出目标运动要素是实现垂直命中的前提条件。为了实现鱼雷的末弹道垂直命中, 需要掌握目标的运动要素, 即雷目距离信息、目标速度及航向角信息。雷目距离由鱼雷自导系统直接给出, 目标速度和航向角信息需要利用自导系统测量参数和控制系统测量参数, 采用递推算法进行估计。

为了对抗鱼雷的攻击, 潜艇一般要进行规避机动。潜艇的最大加速度为0.05 m/s2, 最大旋回角速度为2°/s[2]。目标机动的战术目的是设法摆脱鱼雷的跟踪和攻击, 技术手段则是设法让雷内的各种跟踪解算方法失效[3]。最不利的情况是, 目标发生机动后, 目标的舷别信息会存在一定概率的变化, 这就进一步增加了垂直命中和目标运动要素估计的技术难度。

针对机动目标的运动要素估计, 国内外已有一些研究。目标的模型一般需要和目标的运动状态相匹配, 对于直线运动的目标通常采用匀速(constant velocity, CV)模型或者匀加速(constant accelerate, CA)模型, 对于做转弯运动的目标则可以采用转弯(constant turning, CT)模型。所谓CV、CA和CT模型, 就是假设目标的速度、加速度或者旋回角速度恒定。对于机动目标, 采用CT模型可以较准确地估计出目标的运动要素, 但该模型需要掌握目标的旋回角速度, 可这在实际中是不可预知的, 针对这种情况, 大部分的研究方法就是假设在较短的时间内, 目标的旋回角速度为零, 然后用CA模型求解目标的运动要素。文献[4]假定目标在运动过程中其加速度恒定, 建立目标运动的CA模型, 利用卡尔曼滤波技术解决了目标速度的估计问题。其采用自适应衰减记忆卡尔曼滤波技术, 通过修正卡尔曼滤波器中协方差矩阵实现对机动目标的跟踪; 该算法需要判断目标是否机动, 并确定机动的门限, 相应的算法比较复杂。文献[6]采用CA模型对机动目标进行估计, 实现了对目标蛇形和“Z”字型机动的跟踪。但由于模型不匹配, 存在较大的跟踪误差, 所以需要进一步研究一种新的方法来估计目标的运动要素。

分析表明, 在卡尔曼滤波器启动后的初始阶段, 由于修正估计值的增益矩阵很大, 利用量测值可以对估计值进行较强的修正, 使得估计值比较快地接近实际值; 当初始过程结束后, 增益矩阵的模将逐渐减小, 量测信息只能对估计值进行微小的修正[5]。因此, 如果能够利用卡尔曼滤波器的初始阶段量测信息修正能力强, 而且滤波器对目标运动状态跟踪速度快的特点, 就能够实现对机动目标的快速准确跟踪[7]。

文中以做匀加速转弯运动的目标为例, 采用卡尔曼滤波技术实现对机动目标进行跟踪和定位, 以确定目标运动要素。当采用假定目标运动状态为匀加速度的CA模型时, 由于模型和目标运动状态不匹配, 目标机动后会导致估计结果发散, 即估计误差随时间增大[8]。为了提高对目标的跟踪能力, 文中采用定期重置协方差阵的方法, 即使=0, 可以有效地实现对机动目标的快速准确跟踪, 方法简单, 易于工程实现。

1 卡尔曼滤波器设计及参数选择

1.1 卡尔曼滤波器模型

忽略外界环境对目标运动的干扰, 并假设目标在运动过程中加速度恒定, 采用CA模型描述目标运动, 取目标的位置、速度和加速度为状态变量, 目标运动相应的状态方程为[9]

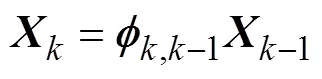
其中

以目标的位置信息为量测变量建立量测方程

卡尔曼滤波的递推公式为[10]

1.2 卡尔曼滤波器参数初始化

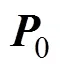
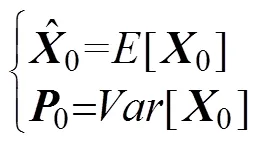
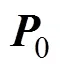
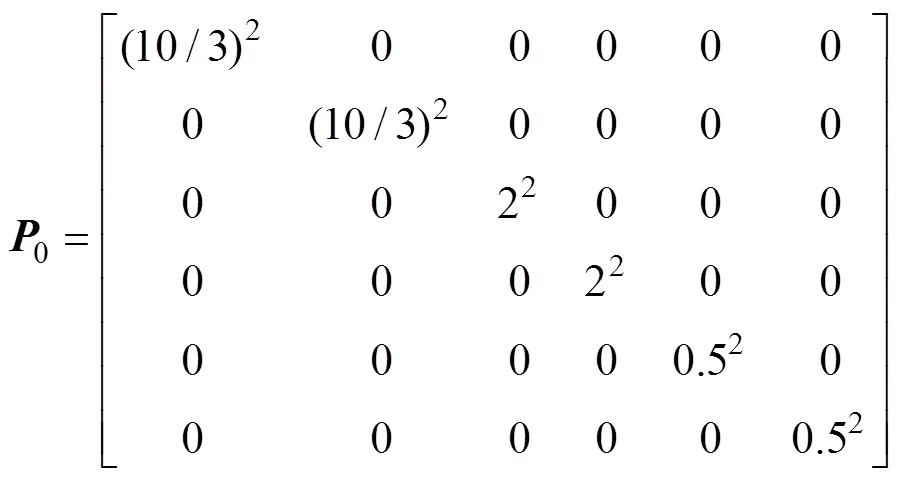
为了使估计结果能更快收敛, 工程上通常以初次检测值0和0为坐标初值, 且认为速度和加速度为0, 状态变量初值

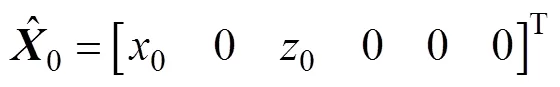
由于鱼雷检测目标通过直接测量, 所以量测矩阵可以取

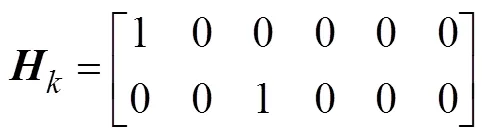
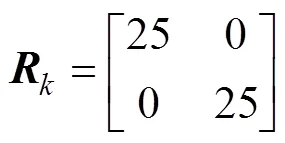
1.3 卡尔曼滤波特性分析及协方差阵的重置

基于CA模型的卡尔曼滤波器只有在启动的初始阶段对做加速转弯的目标有着很好的跟踪效果, 这源于量测值对滤波值有很强的修正能力, 随着时间增加, 该能力逐渐减弱, 最终会导致估计结果发散。由式(5)可知, 量测数据对滤波值的修正能力和增益矩阵密切相关, 具体分析如下。

文中为6×2阶矩阵, 为了便于书写将简化计为, 可展开为

以K21为例, 增益变化曲线如图1所示。

图1中, 在卡尔曼滤波器的初始阶段, 增益很大, 这样利用量测值可以对估计值进行较强的修正, 使得估计值比较快地接近实际值; 当初始过程结束后, 增益将逐渐减小, 量测信息只能对估计值进行微小的修正, 与文献[5]的分析一致。

根据卡尔曼滤波器的初始阶段量测信息修正能力强, 且滤波器对目标运动状态跟踪速度快的特点, 文中对协方差阵采用定期重置的方法, 以实现对机动目标的快速跟踪。所设计的卡尔曼滤波器的估计值在第5个周期可以基本收敛到真值, 因此暂定每10个滤波周期数重置1次协方差阵。

卡尔曼滤波跟踪算法流程图如图2所示。图中为滤波周期数,为重置周期计数器。

图2 定期重置协方差阵的卡尔曼滤波算法流程图

1.4 目标运动要素计算公式

雷目距离由鱼雷自导系统直接给出, 目标的速度和航向角信息需要利用递推算法进行估计。速度和航向角的计算公式为

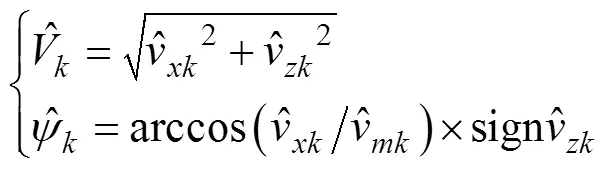
2 仿真结果及分析

为了检验该方法对机动目标运动要素的估计效果, 文中以目标做匀加速直线运动为例进行数学仿真, 具体目标运动参数设定为:

1) 初始速度: 10 m/s;

2) 初始航向角: 60°;

3) 旋回角速度: 2 °/s;

4) 加速度: 0.05 m/s2;

5) 初始距离:轴坐标0为700 m;轴坐标0为200 m;

6) 卡尔曼滤波周期取1 s。

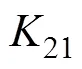
由图3可以看出, 最优增益的值每10个周期会迎来1个峰值, 而其绝对值一直处于一个较高

图3 重置后最优增益K21变化曲线

水平, 这也说明量测值对估计值始终有着很强的修正能力。

随后对机动目标的运动进行估计。目标的实际运动轨迹和卡尔曼滤波估计的轨迹曲线如图4所示。

图4 目标实际运动轨迹和卡尔曼滤波估计轨迹

从图4可以看出, 卡尔曼滤波的估计轨迹和目标的实际运动轨迹基本重合。采用定期重置协方差阵的卡尔曼滤波可以在很短的时间内追踪到目标的运动轨迹, 并且能稳定跟踪下去。因为该方法是以位置作为量测量, 轨迹的基本重合保证了目标估计位置的准确, 可以进行接下来对目标运动要素的估计。

图5和图6分别为目标的速度和航向角估计结果。从图5中可以看出, 由于噪声的影响, 估计值的结果在某些时刻会有较大的起伏, 但总体是围绕着真实值上下波动, 误差基本在2 m/s以内, 且在滤波器启动后很快就达到了收敛。同样的, 由于噪声的影响, 图6中对目标航向角的估计值以目标的实际值为基准浮动, 但误差很小, 且基本在5个周期内就达到了收敛。由此可见, 文中提出的目标运动要素估计算法对目标速度和航向的估计值都能在较短的时间收敛到真值, 快速准确且稳定。

图5 目标速度估计结果

图6 目标航向角估计结果

以上仿真结果表明, 对于机动目标, 采用定期重置协方差阵的卡尔曼滤波技术可以准确快速地得到目标的运动要素, 方法简单可行。

3 结束语

卡尔曼滤波器在滤波初始阶段修正估计值的增益矩阵模很大, 量测值对估计值可以进行较强的修正, 使得估计值比较快地接近实际值。根据这一特点, 文中提出了一种机动目标运动要素的估计方法, 该方法采用卡尔曼滤波并定期对卡尔曼滤波的协方差阵进行重置, 解决了机动目标运动要素的快速准确估计问题, 有效实现对机动目标的快速跟踪, 方法简单, 易于工程实现。数学仿真结果表明, 所设计的估计算法对机动目标具有较强的跟踪能力, 文中给出的方法对研究机动目标运动要素的快速估计具有一定参考价值。

[1] 张秦南, 李建辰, 缪雪佳. 鱼雷实现垂直命中的最优导引技术研究[J]. 鱼雷技术, 2000, 8(1): 18-21.

[2] David V, Stallard S D. Optimal Guidance Law for Low Miss and Perpendicular Impact[J]. IEEE Transactions on Aerospace and Electronic Systems, 1996, 32(4): 1290- 1300.

[3] 夏佩伦. 潜艇对机动目标跟踪和攻击若干问题的探讨[J]. 火力与指挥控制, 2010, 35(2): 6-10.Xia Pei-lun. Some Issues Concerning Maneuvering Target Tracking and Attacking with Submarine[J]. Fire Control & Command Control, 2010, 35(2): 6-10.

[4] 杨向锋, 杨云川, 陈亚林. 水下声自导武器目标跟踪方法研究[J]. 计算机工程与应用, 2013, 49(5): 220-224.Yang Xiang-feng, Yang Yun-chuan, Chen Ya-lin. Study on Target of Acoustic Homing Weapon[J]. Computer Engineering and Applications, 2013, 49(5): 220-224.

[5] Roque J P C. Sensors and Control in the Underwater Intercept and Docking Problems[R]//Thesis and Dissertation Collection. California: Dudley Knox Library, 1995: 25-26.

[6] 高炳祥, 万德均, 周百令. 一种快速有效的捷联系统初始对准算法[J]. 中国惯性技术学报, 1995, 9(3): 8-12.Gao Bing-xiang, Wan De-jun, Zhou Bai-ling. A Fast and Effective Initial Alignment Algorithm for Starpdown System[J]. Journal of Chinese Inertial Technology, 1995, 9(3): 8-12.

[7] 毕进, 雷璐, 郭敏. 基于卡尔曼滤波的机动目标外推预测的研究[J]. 现代电子技术, 2012, 35(11): 42-45. Bi Jin, Lei Lu, Guo Min. Research of Maneuvering Target Extrapolation Based on Kalman Filtering[J]. Modern Electronics Technique, 2012, 35(11): 42-45.

[8] Elsa C, Diana O, Carlos E D. Maneuvering Target Tracking Using Extended Kalman Filter[J]. IEEE Trans. on AES, 1991, 27 (1): 155-158.

[9] 崔诵祺, 安建平, 王爱华. 机动目标模型匹配卡尔曼滤波载波跟踪算法[J]. 系统工程与电子技术, 2014, 36(2): 376-381.Cui Song-qi, An Jian-ping, Wang Ai-hua. Kalman Filter Used for Carrier Tracking Algorithm Based on Matched Maneuvering Target Model[J]. Systems Engineering and Electronics, 2014, 36(2): 376-381.

[10] 周凤岐, 卢晓东. 最优估计理论[M]. 北京: 高等教育出版社, 2009.

[11] Park S E, Lee J G. Improved Kalman Filter Design for Three-Dimensional Radar Tracking[J]. IEEE Trans. Aer- ospace and Electronic Systems, 2001, 37(2): 727-739.

An Estimation Algorithm of Maneuvering Target Movement Elements

CHENG Shuai, ZHANG Qin-nan, WANG Li-wen

(The 705 Research Institute, China Shipbuilding Industry Corporation, Xi’an 710077, China)

For estimation of maneuvering target movement elements, the Kalman filter method based on the uniform acceleration model has more applications, however, due to the defect of Kalman filter itself, this method is only applicable to the target with uniform acceleration in the straight line movement situation, but is impossible to estimate the motion elements of the target in turning. In order to overcome this problem, an estimation algorithm of maneuvering target movement elements is proposed in this paper. Through periodic reset of the covariance matrix of Kalman filtering, the algorithm can make the absolute value of the gain matrix always keep larger, make the correction effect of estimation at a satisfactory level, and ultimately solve the estimation problem of maneuvering target movement elements including turning movement. Mathematical simulation results show that the proposed estimation algorithm has strong tracking ability for maneuvering target, and meets the requirement of estimation error. It is simple and easy to be realized in engineering.

target movement elements; estimation algorithm; uniform acceleration; turning movement; Kalman filter

TJ630.34; TB565.2

A

2096-3920(2020)01-0046-05

10.11993/j.issn.2096-3920.2020.01.007

程帅, 张秦南, 王立文. 一种机动目标运动要素估计算法[J]. 水下无人系统学报, 2020, 28(1): 46-50.

2019-08-22;

2019-10-21.

程 帅(1995-), 男, 在读硕士, 主要研究方向为水下航行器制导技术.

(责任编辑: 许 妍)