战术数据链网络的介质访问控制层优化控制及性能分析

杨志军， 刘征， 丁洪伟， 柳虔林，3

(1.云南大学 信息学院， 云南 昆明 650500；2.云南省教育厅 科学教育研究院， 云南 昆明 650223；3.云南省军区， 云南 昆明 650051)

0 引言

战术数据链是以满足联合作战为主要目的，应用于战术级作战区域，通过传输标准格式数字信号提供平台间实时或准实时战术数据交换和分发，实现态势共享、指挥控制、战术协同的数据通信链路[1-2]。在现代战争中，胜负不再仅依赖于武器的先进性和参战人员规模，而是更加依赖于对战场信息收集与传递的战术数据链。通过战术数据链可以实现陆海空三军协调作战一体化。自20世纪50年代以来，以美国为首的北约等国一直研制使用战术数据链，其中有Link-4A(TADIL C)、Link-11(TADIL A/B)、Link-16(TADIL J)和Link-22(TADIL FJ)等[3]。

轮询作为一种信道接入控制方法，可以实现信道资源的有效分配[4-6]。由于轮询接入控制协议的低时延性和公平性，美军将其应用于Link-11等数据链系统中。但是，单一的轮询接入控制协议不能灵活地分配信道资源，只会按照顺序依次分配信道资源。在战场中肯定会有一些命令的优先级明显高于其他命令的优先级，即某前哨站点收集到的信息重要程度很高且必须要及时传递到网络控制站点(简称网控站点)，由于单一的接入控制协议，该信息可能延长一段时间才能被传递，由此而耽误战机。为解决这类问题，要对前哨站点区分优先级，对收集重要信息的前哨站点给予高优先级，对收集其他信息的前哨站点给予低优先级。很显然，单一的轮询控制系统不能实现该功能。因此，在战术数据链中，对区分优先级的两级轮询接入控制协议的研究是非常有必要的。

轮询接入控制协议有3种不同的基础模型，分别是完全接入控制、门限接入控制和限定接入控制，且这3种接入控制策略适用于不同环境中[7]。完全接入控制是指该信道资源一直被一个站点占用，直至该站点发送完站点内所有信息分组。采用这种策略的系统平均排队队长(一个站点内等待发送的平均信息分组数)和平均等待时间(进入站点的信息分组等待发送的平均时间)最短，非常适用于收集信息少但信息重要程度高的站点。门限控制策略是指一个站点占用信道直至该站点发送完其占用信道那一时刻站点内所有的信息分组数，采用这种策略的系统性能在3种策略中居中。限定接入控制策略是指一个站点占用信道直至该站点发送完一个信息分组数，采用这种策略的系统平均排队队长和平均等待时间最长，但是公平性最好，适用于收集信息少且要求站点间公平的系统[8-10]。

战术数据链中，各个前哨站点一直在收集信息，所要传递的信息分组数较多，而限定K=1(K为站点一次服务时间内发送的信息分组个数)控制策略则规定一个站点一次只能发送一个信息分组数，增加了系统在前哨站点间的查询转换时间，降低了系统接入效率。因此，本文根据数据链数据流较大的特点，结合3种控制策略的各自特点，提出一种基于完全控制策略和非对称门限控制策略的区分优先级两级轮询接入控制系统[11-13]。在该系统模型中，处于低优先级的前哨站点(N个)即为普通站点采用非对称门限控制策略，处于高优先级的前哨站点(1个)即为中心站点采用完全控制策略。在普通站点占用完信道资源后，网控站点将信道资源分配给中心站点，在该站点发送完信息分组数后，网控站点将信道资源又分给下一个普通站点。针对上述过程，本文首先建立该系统的数学模型，再求解出系统重要性能参数平均排队队长的精确表达式和平均等待时间的近似表达式。最后，通过MATLAB仿真软件对理论结果进行验证，对新系统性能进行分析。

在现有国内外文献中，大多数都是从离散时间角度对系统进行分析。本文在信息分组以连续时间规律到达系统的基础上对系统进行分析，仿真实验结果表明理论结果与仿真结果高度吻合。

1 系统模型

1.1 系统网络及轮询控制模型

在战术数据链网络中，指定一个节点为网控站点，网内其他节点为前哨站点(或从属站点)。网控站点控制接入网中所有其他站点对网络的访问，其拓扑结构图如图1所示[14]。针对前哨站点的优先级问题，指定前哨站点中的一个为中心站点，主要负责对重要程度较高的信息采集，其拓扑结构图如图2所示。战术数据链的介质访问控制(MAC)层主要负责信道资源分配，其协议描述了节点接入信道的规则，采取合理的MAC协议可以高效地分配信道资源，有效保证战术数据链的实时性。

图1 网络结构拓扑图Fig.1 Topological graph of network structure

图2 具有优先级的网络结构拓扑图Fig.2 Topological graph of prioritized network structure

在图2中，战术数据链网络中有一个网控站点、一个高优先级前哨站点和N个低优先级前哨站点。根据本文设定的新的轮询接入控制系统，N个低优先级前哨站点即普通站点采用非对称门限接入控制策略，一个高优先级前哨站点即中心站点采用完全服务，一个网控站点即服务器控制其内站点对网络的访问。根据实际战场情况，设定各个站点的到达率、服务率和转换率都互不相同。在该轮询接入控制系统中，普通站点的序号由{1,2,3,…,N}表示，中心站点的序号由h表示，站点服务顺序为：1→h→2→h→…→N→h→1，即普通站点i(i=1,2,3,…,N)在占用完信道后，服务器将信道资源分配给中心站点h，中心站点发送完信息分组数后，服务器又将信道资源分配给普通站点i+1. 在上述过程中，中心站点在发送信息分组数的同时，服务器也在对下一个等待发送的普通站点i+1进行查询；当中心站点占用完信道后，服务器直接将信道资源分配给i+1站点，该站点可直接发送信息分组数，系统模型示意图如图3所示。图3中，下标序号表示前哨站点序号，λ表示一个时隙内进入前哨站点的平均信息分组个数，β表示前哨站点传输一个信息分组所需要的平均时间，γ表示由低优先级前哨站点转向高优先级前哨站点所需要的平均查询转换时间，N为低优先级前哨站点的序号，h为高优先级前哨站点的序号。

图3 连续两级非对称轮询系统模型Fig.3 Continuous two-stage asymmetric polling system model

设定在tn时刻，低优先级前哨站点i(i=1,2,3,…,N)开始占用信道，定义随机变量ξi(n)为该前哨站点中等待传输的信息分组数，随机变量ξh(n)为高优先级前哨站点h中等待传输的信息分组数，则整个系统状态的随机变量为{ξ1(n),ξ2(n),…,ξN(n),ξh(n)}；设定tn*时刻，低优先级前哨站点i占用完信道，网控站点将信道资源分配给站点h，定义此刻的系统状态随机变量为{ξ1(n*),ξ2(n*),…,ξN(n*),ξh(n*)}；设定tn+1时刻，站点h传输完站内所有信息分组数，站点i+1开始占用信道资源，定义此刻的系统状态随机变量为{ξ1(n+1),ξ2(n+1),…,ξN(n+1),ξh(n+1)}.

系统的状态可以用马尔可夫链描述，该马尔可夫链是非周期的和各态历经的[15]。

1.2 系统工作条件

根据战术数据链网络的数据流特点，同时结合轮询控制机制及其特点，对系统模型进行如下设定：

1)进入每个前哨站点内等待传输的信息分组到达服从相互独立的泊松分布，且对于站点i(i=1,2,3,…,N,h)到达率为λi；

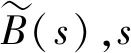
4)高优先级前哨站点对在任一时隙内到达的信息分组进行完全服务所需时间的随机变量服从一个相互独立且同分布的概率分布，其分布的概率母函数为H(z)；

5)服务系统中任何一个队列的缓存容量足够大，不存在信息分组丢失的情况；

6)每一个加入进队列的信息分组，将会按照先到先服务(FCFS)的方法接受服务。

定义随机变量如下：

ui(n)：网控站点将信道资源分配给高优先级前哨站h前，从低优先级前哨站i查询转换到该站点所耗费的时间；

vi(n)：低优先级前哨站点i占用信道资源时传输信息分组数所耗费的时间；

vh(n*)：高优先级前哨站点h占用信道资源时传输信息分组数所耗费的时间；

μj(ui)：在ui(n)时间内进入前哨站点j(j=1,2,…,N,h)的信息分组数；

ηj(vi)：在vi(n)时间内进入前哨站点j(j=1,2,…,N,h)的信息分组数；

ηj(vh)：在vh(n*)时间内进入前哨站点j(j=1,2,…,N,h)的信息分组数。

1.3 数学模型建立

在系统工作过程中，已知该轮询系统的状态随机变量及其概率分布的各阶特性，因此为求解系统重要性能参数，概率母函数是一种非常重要的工具。

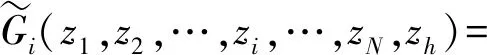
(1)

式中：πi(x1,x2,…,xi,…,xN,xh)表示系统状态概率分布。

对连续时间型系统进行分析时，需要对系统关键参数进行LST。函数的LST定义为

(2)

式中：f(t)为连续时间函数。

对于以参数λ到达的泊松过程，时间t内到达的顾客数对应的概率母函数为

(3)

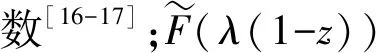
在tn*时刻，高优先级前哨站点h开始传输信息分组时，系统状态变量的概率母函数为

(4)

在tn+1时刻，i+1站点开始传输信息分组时，系统状态变量的概率母函数为

(5)

2 轮询系统的1阶和2阶特性

2.1 平均排队队长

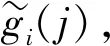
(6)

根据(4)式、(5)式和(6)式，得到低优先级前哨站点i的平均排队队长的表达式为

(7)

同理，可得高优先级前哨站点h的平均排队队长的表达式为

(8)

2.2 2阶偏导量

(9)

(10)

(4)式和(5)式分别代入(9)式和(10)式，得

(11)

(12)

(13)

2.3 平均等待时间

信息分组的等待时间是指一个信息分组从进入一个前哨站点到其被传输的等待时间，平均等待时间是指进入一个前哨站点的所有信息分组数等待的平均时间。本文中Ti和Th分别表示低优先级前哨站点i与高优先级前哨站点h的平均等待时间，根据文献[19]和文献[20]，可得其平均等待时间为

(14)

(15)

3 仿真实验及性能分析

3.1 仿真实验

为验证理论分析的正确性以及对基于连续时间区分优先级的轮询控制系统性能分析，本文通过MATLAB 2014a软件进行仿真实验。在第2节理论分析过程中已经作了一些条件设定，同理，针对仿真实验也需要满足以下条件[15，21]：

1)各站点的参数变量都服从相同的分布，普通站点之间的到达率相同但与中心站点的到达率不同；

2)任一时隙内进入各站点的数据信息量都满足泊松分布；

3)轮询系统满足稳态条件：

在本文仿真环境中，所有信息分组都能发送成功，归一化处理后时间轴按时隙划分，定义一个时隙为20 μs，信息分组的长度为1 100 Byte. 在仿真实验中：首先，对第2节理论分析结果进行验证，分别对有7个低优先级前哨站点和1个高优先级前哨站点以及有5个低优先级前哨站点和1个高优先级前哨站点的系统进行仿真实验，系统初始条件设定以及结果对比如表1、表2所示，表1、表2中高优先级站点序号表示为低优先级前哨站点转高优先级前哨站点时，高优先级前哨站点的状态；其次，在低优先级前哨站点5个和高优先级1个的仿真环境中，通过改变系统中的总负载以及前哨站点的到达率、负载，观察分析平均排队队长和平均等待时间的变化规律，如图4～图9所示；最后，将包含有5个普通前哨站点的1级非对称门限接入控制系统与包含有低优先级前哨站点5个和高优先级1个的新系统进行对比，结果如表3所示。

表1 低优先级前哨站点为7的仿真值与理论值对比Tab.1 Experimental and theoretical values of Outpost 7 of polling system

表2 低优先级前哨站点为5的仿真值与理论值对比Tab.2 Experimental and theoretical values of Outpost 5 of polling system

图4 低优先级前哨站点到达率设置Fig.4 Arrival rate setting of low priority outposts

图5 低优先级前哨站负载设置Fig.5 Load setting of low priority outposts

图6 总负载对低优先级前哨站点平均排队队长的影响Fig.6 Impact of total load on average queue length of low priority outposts

图7 总负载对高优先级前哨站点平均排队队长的影响Fig.7 Impact of total load on average queue length of high priority outpost

图8 总负载对低优先级前哨站点平均等待时间的影响Fig.8 Impact of total load on average waiting time for low priority outposts

图9 总负载对高优先级前哨站点平均等待时间的影响Fig.9 Impact of total load on average waiting time for high priority outposts

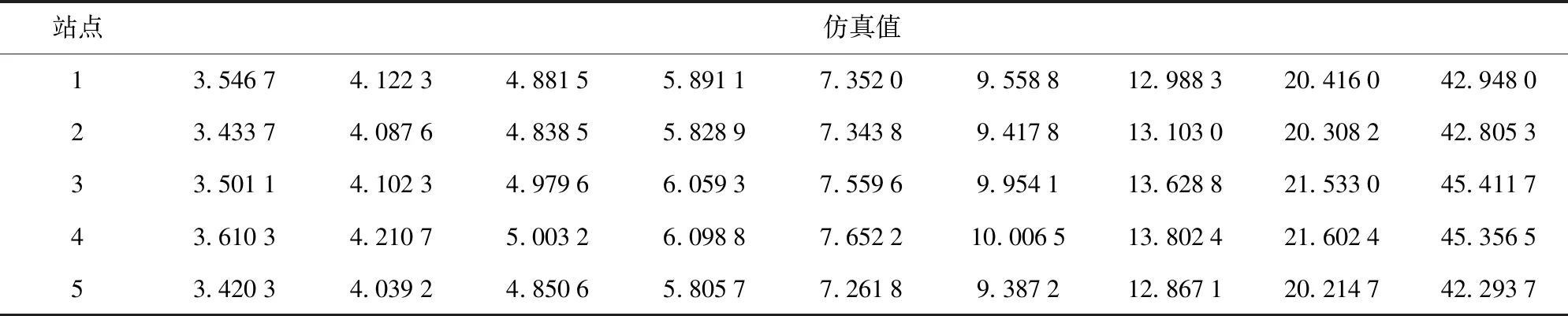
表3 低优先级前哨站点平均等待时间仿真值Tab.3 Simulated average waiting time values of low priority outposts 时隙

3.2 性能分析

1)在表1、表2中，对低优先级前哨站点个数分别为7、5的轮询系统进行了实验，实验结果表明系统重要性能参数的理论值与仿真值的差值极小，在误差范围内，验证了系统理论分析的正确性与系统的可行性。

2)在图4～图9中，本文将系统总负载按照0.1的间隔从0.1逐次增加至0.9，其中图4和图5分别为系统低优先级前哨站点的到达率和负载设定。从图6～图9中可以看出：各前哨站点内等待发送的信息分组平均个数以及进入各前哨站点内的信息分组等待发送的平均时间随着总负载增大而逐渐增大，在总负载越接近1的情况下，系统性能受到总负载的影响越大；对比图4与图6可以发现，到达率越大，低优先级前哨站点的平均排队队长越长；比较图4、图5与图7、图9可以发现，高优先级前哨站的平均排队队长和平均等待时间受到低优先级前哨站点到达率和负载影响，在总负载较低时到达率的影响较大；由图8可以看出，平均等待时间都相差不多，这是因为各个低优先级前哨站点的负载差距不大，所得平均排队队长差距较小，很难从图中分辨，但是，根据图5以及表3易得，低优先级前哨站点的负载越大其平均等待时间越长。

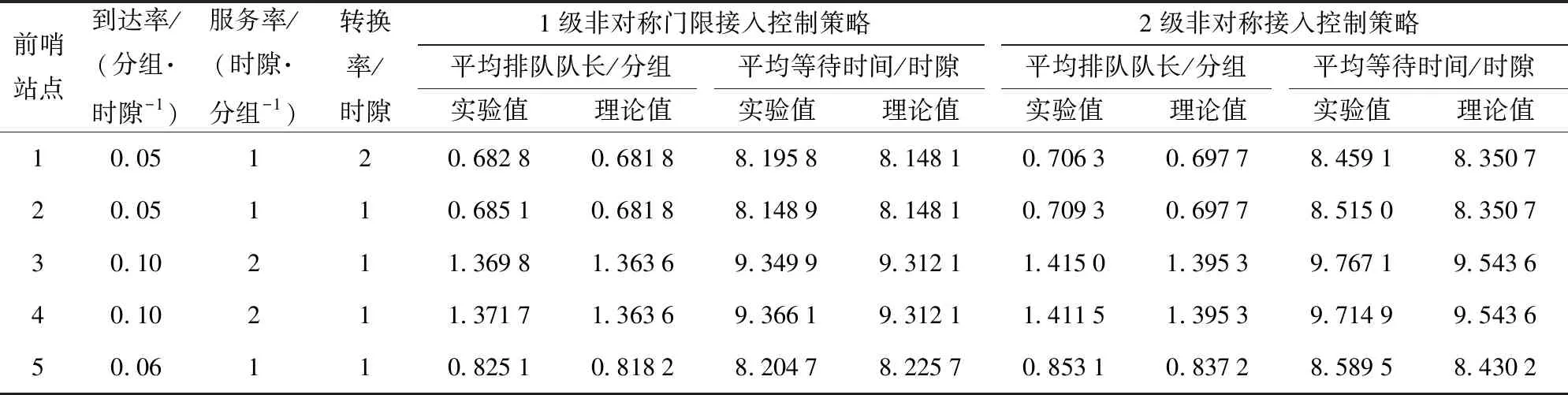
表4 两种接入控制策略的比较Tab.4 Comparison of two access control strategies

3)表4中对1级非对称门限接入控制策略的系统与本系统进行了对比，观察了高优先级前哨站点对低优先级前哨站点的影响。为了保证实验的客观性，该仿真实验中，两个系统初始系统条件设定相同。由表4中的数据可以看出，当高优先级前哨站点的负载远小于总负载时，低优先级前哨站点的性能参数与1级门限接入控制策略的系统性能参数接近。

4)从图6～图9、表1～表4中可以看出，高优先级前哨站点的所有性能参数值都优于低优先级前哨站点的性能参数值，表明该系统即可以保障高优先级前哨站点内的信息分组在较短时间内传输，也能让低优先级前哨站点之间公平传输，达到了高优先级前哨站点高服务质量、低优先级前哨站点之间公平享受服务的目的。

4 结论

本文根据战术数据链的数据流特点，针对其前哨站点优先级问题以及系统实用性，对战术数据链的媒介接入控制层接入控制协议采取了一种区分优先级的两级非对称轮询接入控制系统。从连续时间角度对系统进行了数学分析，得到其重要性能参数的数学解析式，通过MATLAB软件并根据系统模型进行了仿真实验，验证了理论分析的正确性。通过分析可知：系统总负载对系统的所有性能参数都有影响，且总负载越接近1，对系统性能影响越大；低优先级前哨站点的平均排队队长由其到达率决定，到达率越大其平均排队队长越大，但是，其平均等待时间是由负载决定；高优先级前哨站点的平均等待时间和平均排队队长受到低优先级前哨站点的到达率和负载的影响，且总负载越接近1，受到负载的影响越大；通过1级门限接入控制系统与该系统比较可以看出，两个系统的重要性能参数差距不大，表明该系统在保障低优先级前哨站点服务质量的情况下，可为高优先级前哨站点提供较高的服务质量，且其针对实际环境中各低优先级前哨站点条件不同的情况，对低优先级前哨站点采用非对称门限服务，增强了系统实用性。

需要说明的是，在对系统的平均等待时间进行数学解析式求解时，对其2阶特性量采取了一种基于循环查询周期的近似分析方法，根据仿真值与理论值比较，该方法合理有效。但是，2阶特性量的近似方法不仅局限于这一种方法，还有其他方法可以探索。对于该接入控制系统，其不仅解决战术数据链网络中前哨站优先级问题，而且其非对称特性还增强了系统的实用性。