基于速度约束与模糊自适应滤波的车载组合导航

胡杰， 严勇杰， 王子卉

(1.中国电子科技集团公司 第二十八研究所 空中交通管理系统与技术国家重点实验室， 江苏 南京 210007；2.东南大学 微惯性仪表与先进导航技术教育部重点实验室， 江苏 南京 210096)

0 引言

捷联惯性导航系统(SINS)和全球定位系统(GPS)是两种常用的导航定位系统，其中：GPS定位精度高，且位置误差不随时间积累，但是卫星信号易受多路径、建筑物遮挡等干扰影响，导航系统的鲁棒性较差[1]；SINS具有全自主、全天候、隐蔽性强等优点，但其惯性测量单元(IMU)漂移会引起位置随时间积累性误差[2]。考虑到这两种导航系统的互补性，SINS和GPS组合后的性能更优，目前广泛应用于航空航天、测绘等军民用领域，能够连续输出运载体速度、位置和姿态等信息，具有精度高、抗差性强等优点[3]。

当GPS信号不可用时，组合导航系统将切换至纯惯性工作模式。针对GPS失效引起的导航系统精度降低问题，国内外学者进行了相关研究。严恭敏等[4]、肖烜等[5]和Liu等[6]提出利用里程计辅助车载SINS实现长时间导航与定位；高钟毓等[7]首次提出在车载组合导航系统中利用车辆停车时速度为零这一约束条件估计导航系统误差，该方法需要每间隔一段时间停车一次，影响载车机动性能[8]。近年来，随着人工智能(AI)算法的日渐成熟，许多学者提出利用AI模块辅助增强组合导航系统卫星失效时的性能。当GPS信号有效时，AI模块利用观测数据进行训练；一旦GPS信号失效，利用训练得到的导航信息对SINS误差进行校正。Zhang等[9]和Chen等[10]分别提出利用模糊神经网络和遗传算法训练系统模型，并在卫星失效时对SINS误差进行校正，实现了车载无缝定位。其他一些学者也纷纷开展了基于AI算法的组合导航系统研究工作，比如集成学习算法[11]、小波神经网络[12]、多层感知机算法[13]等，但是AI算法计算量较大，实现过程比较复杂，在实际系统中使用时存在局限性。

Kalman滤波算法是一种常用的多源信息融合方法，目前在GPS定位[14]、组合导航[15]等方面得到广泛应用。Kalman滤波器状态收敛速度和精度受限于系统噪声与量测噪声统计精度，为获取滤波过程中噪声特性，Sage等[16]提出了一种自适应Kalman滤波(ADKF)算法，该方法在线计算系统噪声与量测噪声协方差矩阵，分析可知， ADKF无法同时估计系统噪声与量测噪声协方差矩阵。徐田来等[17]提出将简化ADKF与交互式多模型(IMM)相结合，以ADKF估计得到的粗略噪声协方差矩阵为中心进行IMM估计，该方法能够较好地解决模型参数不确定性问题，但是该方法计算量大。王向华等[18]提出利用并行Kalman滤波器实现量测噪声协方差矩阵的自适应调节，需要在滤波估计时并行使用Kalman滤波器。

本文针对车载GPS失效时SINS精度降低问题，提出一种采用车辆速度约束辅助的组合导航方法，在不增加外部传感器的前提下，提高SINS导航精度。同时针对SINS/GPS组合导航中量测噪声的不确定性以及由此引起的导航精度降低问题，提出了一种基于模糊推理系统(FIS)的ADKF算法，对算法性能进行了仿真验证，并进行了实际系统验证试验。

1 SINS/GPS组合模型

1.1 系统状态方程

(1)

进一步根据SINS误差方程[19]，并结合系统状态向量可以得到组合导航滤波状态方程为

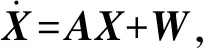
(2)

式中：A为SINS误差方程对应的状态转移矩阵；W为系统噪声矢量。

1.2 系统量测方程

1.2.1 卫星有效

卫星信号有效时利用GPS接收机输出速度和位置作为滤波器观测值，此时量测方程为

Z1=H1X+V1，

(3)

式中：Z1为卫星有效时观测向量，Z1=[(δPn)T(δVn)T]T，其中δPn、δVn分别为导航坐标系n系中的3个位置和速度误差；H1为量测矩阵，H1表达式为

(4)

I3×3表示3×3维单位矩阵，03×3、03×9分别表示3×3和3×9维零矩阵；V1为系统量测噪声矢量。

1.2.2 卫星失效

卫星信号失效时利用车辆行驶特点抑制SINS误差[20]，如果车辆没有发生侧滑和跳跃，则车体坐标系b系中侧向速度与天向速度可近似为0 m/s，如图1所示，由于仅侧向和天向两个方向存在约束，因此该方法也被称为非完整性约束。

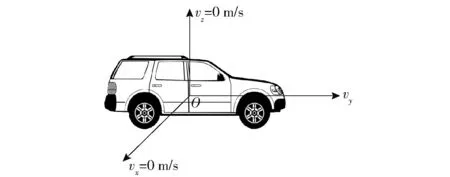
图1 车辆运动学约束Fig.1 Vehicle kinematics constraints

IMU安装于车辆后首先进行安装误差标校，因此假设IMU的测量轴与b系重合，则可得b系下的速度分量为

(5)

对(5)式进行全微分，则有

(6)

式中：δvb表示b系中速度误差分量；φn表示数学平台失准角向量；δvn表示n系中速度误差分量；“×”表示取对应3维向量的反对称矩阵。

将(6)式改写成

δvb=M1δvn+M2φn，

(7)

式中：

(8)

(9)

利用车辆运动学约束条件构成滤波器量测值为

(10)

由(7)式和(10)式可得量测方程为

Z2=H2X+V2，

(11)

式中：H2为量测矩阵，H2表达式为

(12)

M1(1,)、M2(1,)分别表示取矩阵M1、M2的第1行，M1(3,)、M2(3,)分别表示取矩阵M1、M2的第3行，01×3、01×6分别表示1×3维和1×6维零矩阵；V2为系统量测噪声矢量。

对(2)式、 (3)式和(11)式进行离散化，可以得到组合导航状态方程和量测方程的离散形式为

Xk=Φk,k-1Xk-1+Wk-1，Zk=HkXk+Vk，

(13)

式中：Xk表示k时刻系统状态矢量；Φk,k-1表示离散方程k-1时刻至k时刻转移矩阵；Xk-1表示k-1时刻系统状态矢量；Wk-1表示系统噪声矢量；Zk表示k时刻量测矢量；Hk表示k时刻量测矩阵；Vk表示k时刻量测噪声矢量。

根据上述分析可知，当车辆急速拐弯时，其向心加速度使得车体侧向速度不为零，此时不能满足上述约束条件。一般情况下，急速拐弯时间较短，因此短时间内可只进行纯惯性解算，待车辆运行状态平稳时，切换至非完整性约束模式，可以根据IMU输出信号判断车辆是否处于急拐弯状态。

由牛顿第二运动定律可得车辆向心加速度为

a(t)=v(t)×ωz(t)，

(14)

式中：a(t)表示t时刻车辆向心加速度；v(t)表示t时刻车辆行驶速度；ωz(t)表示陀螺输出z轴向车辆角速度。

根据实际路况以及多次实验数据统计结果可以确定向心加速度检测阈值λa，如果|a(t)|≥λa，说明检测得车辆急速拐弯，此时切换至“仅时间更新的非完整性约束”，即不进行滤波器量测更新，仅进行时间更新[21]，否则进行非完整性约束。

综上所示，可以得到基于速度约束的组合导航系统量测更新流程示意图，如图2所示。

图2 基于速度约束的组合导航系统量测更新流程Fig.2 Measurement updating process of integrated navigation system based on velocity constraint

2 基于FIS的ADKF算法

Kalman滤波器被广泛应用于组合导航系统中，根据系统状态方程、量测方程以及噪声先验统计特性可以估计得到最优状态值。然而由于导航系统具有时变性，其量测噪声特性受外界环境影响较大，因此需要在线调节量测噪声协方差矩阵大小，使其能够适应外界环境变化。新息序列能够实时反应量测噪声统计特性的变化，因此可以根据新息序列的变化在线调节量测协方差矩阵。

Kalman滤波器量测更新中新息序列可表示为

ek=Zk-Hkk/k-1，

(15)

式中：ek表示k时刻滤波器新息序列；k/k-1表示k时刻滤波器状态一步预测值。

定义新息序列实际协方差与理论协方差之间的不匹配度为

(16)

式中：DoMk[i]表示k时刻第i个量测值的不匹配度；Sk、k分别为k时刻新息序列的理论与实际协方差矩阵；Sk[i,i]、k[i,i]表示对应矩阵的对角元素；1≤i≤m，其中m表示观测向量的个数。

新息序列实际协方差矩阵可计算为

(17)

式中：N为平滑窗口大小，该值需要根据经验确定；N值越大，平滑后噪声越小；N值越小，其跟踪能力就越强；本文根据试验取N值为15.

新息序列理论协方差矩阵可计算为

(18)

式中：Pk/k-1表示k时刻状态一步预测协方差矩阵；Rk表示k时刻量测噪声协方差矩阵。

由 (16) 式知，DoMk是一个维数为m的向量，取其平均值作为FIS的输入，即定义一个新的变量AveDOMk，其表达式为

AveDoMk=‖DoMk‖1/m，

(19)

式中：‖·‖1表示计算向量的1范数，根据AveDOMk值的大小可以判别滤波器的收敛情况，AveDOMk=1表示此时滤波器严格收敛，否则表示滤波器异常。

由(19)式可知，当AveDOMk1时，说明系统量测噪声增大，此时需要调大量测噪声矩阵，而当AveDOMk1时，说明系统量测噪声减小，此时需要调小量测噪声矩阵，最终保持AveDOMk值在1附近，由此可以得到自适应滤波递推形式为

时间更新：

k/k-1=Φk,k-1k-1，

(20)

(21)

量测更新：

(22)

k=k/k-1+Kk[Zk-Hkk/k-1],

(23)

Pk=Pk/k-1-KkHkPk/k-1,

(24)

Rk=cRk-1,

(25)

本文采用FIS根据输入的AveDOMk值确定在线调整系数c，其实现过程如下：

1)定义模糊集合，设decrease表示小于1的模糊子集，keep表示等于1的模糊子集，increase表示大于1的模糊子集。

2)确定FIS隶属度函数与模糊规则。

3)去模糊化以获得对应的量测噪声协方差矩阵在线调整系数，本文调整系数c规则为：

IfAveDOMkis decrease, thencis decrease；

IfAveDOMkis keep, thencis keep；

IfAveDOMkis increase, thencis increase.

其采用的隶属度函数如图3所示。

图3 FIS输入输出变量隶属函数Fig.3 Membership functions of input and output variables of FIS

综上所述，图4为基于速度约束和FIS-ADKF的SINS/GPS组合导航系统结构图。

图4 SINS/GPS组合导航系统框图Fig.4 Block diagram of SINS/GPS integrated navigation system

由图4可以看出，当卫星信号有效时，利用GPS速度和位置信息与SINS输出速度和位置信息进行组合，一旦卫星信号失效，此时需要检测车辆急速转弯，如果车辆行驶较为平稳，则利用虚拟侧向和天向速度辅助SINS进行导航与定位。同时新息序列实际协方差矩阵与理论协方差矩阵之比作为模糊推理系统输入，利用FIS可以得到量测噪声协方差矩阵调整系数，从而实现Kalman滤波器最优估计。

3 算法仿真与性能分析

通过改变量测噪声值对本文所提出算法进行验证，假设陀螺常值漂移为0.01°/h，角度随机游走系数为0.005°/h1/2，标度因数误差为50×10-6；加速度计常值偏置为100×10-6g，随机游走系数为80×10-6g·s1/2，SINS“数学平台”初始失准角分别为0.5′、0.5′以及3′.

车辆运行速度为5 m/s，基准速度和位置根据GPS速度和位置误差模型仿真得到，并分别假设：速度误差均值为0.1 m/s，标准差为0.1 m/s；位置误差均值为0.5 m，标准差为0.1 m；初始航向角、俯仰角以及横摇角分别为30°、1°以及1°，Kalman滤波周期设置为1 s，仿真时间为2 400 s.

仿真过程中，在0～900 s之间保持模型准确，在900～1 500 s之间设置量测噪声标准差为初始时刻的5倍，即速度和位置量测噪声分别为0.5 m/s和0.5 m，在1 500～2 400 s之间量测噪声标准差恢复为初始值，分别利用标准Kalman滤波和本文所提出的FIS-ADKF对上述过程进行仿真，图5为设定的车辆行驶轨迹二维图，图中蓝色实线和红色点划线分别为标准Kalman滤波和FIS-ADKF解算得车辆行驶轨迹。表1为位置误差标准差对比统计，图6为位置误差对比曲线。

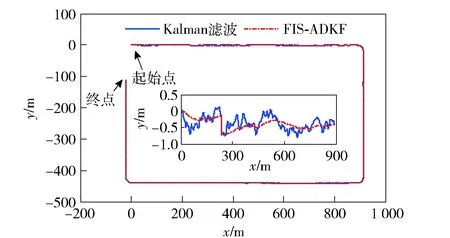
图5 车辆行驶轨迹二维图Fig.5 2-D map of vehicle trajectory

图6 位置误差对比曲线Fig.6 Contrast curves of position errors

由图6以及表1可以看出，在时间1～900 s之间，由于模型较为准确，标准Kalman滤波与本文所提出的FIS-ADKF精度相当。在900～1 500 s之间，由于量测噪声发生变化，标准Kalman滤波器的量测噪声协方差矩阵无相应变化，所以Kalman滤波器的估计性能受到较大影响，输出速度与位置等参数均出现较大偏差，同样条件下，FIS-ADKF由于可以通过实时估计新息序列协方差使其逼近外部实际噪声，然后进一步通过减小量测增益矩阵以削弱量测噪声对滤波器估计精度影响，因此滤波器具有较高的估计精度和抗干扰性。

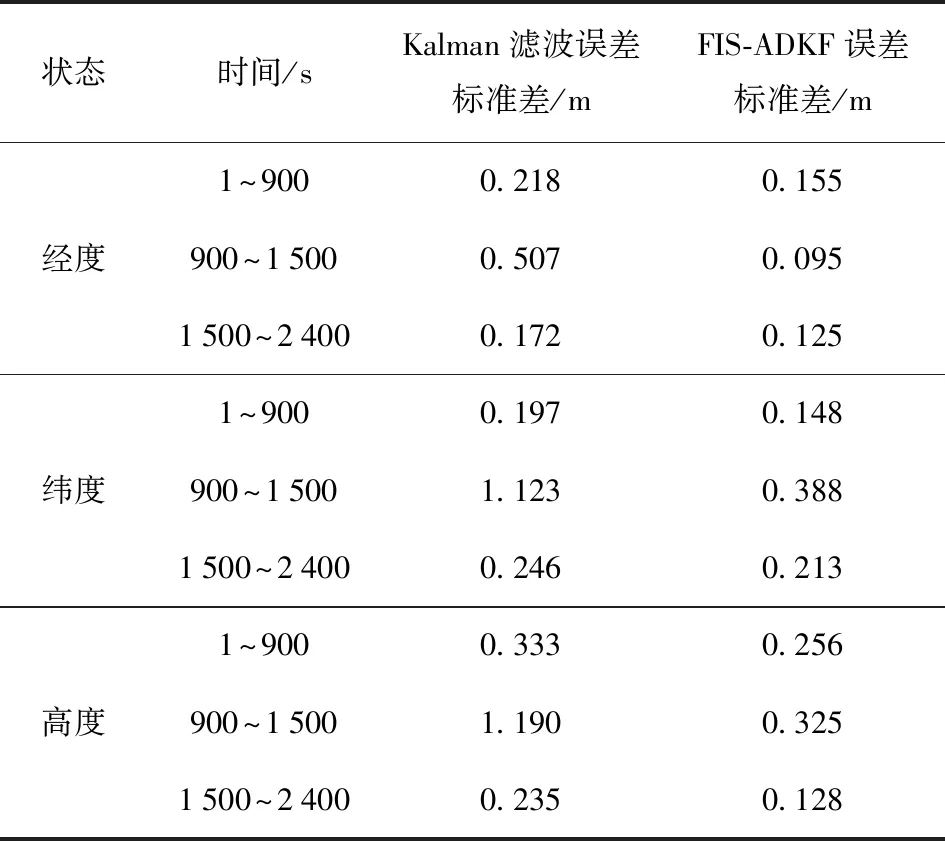
表1 位置误差标准差对比统计Tab.1 Statistical comparison of standard deviations of position errors

4 验证试验

利用实验室研制的光纤SINS进行车载组合导航验证试验，其IMU由3个光纤陀螺和3个石英挠性加速度计组成，同时试验车上有一台GPS接收机，其位置精度优于5 m，IMU主要性能指标如表2所示。

表2 光纤SINS参数Tab.2 Parameters of optical fiber SINS

为了获取车辆行驶过程中真实位置，根据GPS接收机保存的原始观测数据并利用后处理的动态定位方法(PPK)计算车辆位置信息。车载试验实物图如图7所示，车载试验地点为贵阳市某条道路，车载试验行驶过程中控制车辆速度为10 km/h，试验时长为3 600 s.

图7 试验设备及环境Fig.7 Experimental facilities and environment

试验路段卫星无遮挡，因此在时间点1 500 s设定卫星信号不可用，持续时间600 s，该时间段内车辆无拐弯现象。图8为卫星信号失效时无速度约束位置误差曲线，图9为采用速度约束辅助标准Kalman滤波与本文所提出的FIS-ADKF算法所得位置误差对比曲线，表3为卫星信号失效时无速度约束辅助、速度约束辅助标准Kalman滤波算法以及速度约束辅助FIS-ADKF算法位置误差对比统计。

图8 无速度约束位置误差曲线Fig.8 Position errors without velocity constraint

图9 不同滤波方法位置误差对比曲线Fig.9 Contrast curves of position errors of different filtering methods

表3 最大位置误差对比统计Tab.3 Statistical comparison of maximum position errors

由图8可以看出，当卫星信号失效时，SINS工作于纯惯性导航模式，其位置误差随时间积累，当卫星信号恢复后，组合导航系统位置误差能够较快收敛，试验结果与理论分析一致。

由于SINS纯惯性模式下高度通道发散，因此表3中未给出纯惯性模式下的高度误差结果。由图9和表3可以看出，当利用侧向与天向速度组合后，SINS导航精度得到提高，纬度最大误差由41.33 m减小至8.61 m，经度最大误差由17.65 m减小至2.56 m. 同时本文所提出的基于FIS-ADKF的组合导航精度要优于标准Kalman组合精度，尤其在GPS信号遮挡期间，由于滤波器量测信息不确定性较大，采用基于FIS-ADKF算法的经度误差由2.56 m减小为0.72 m，纬度误差由8.61 m减小为3.42 m，高度误差由2.52 m减小为0.86 m，验证了本文所提出自适应滤波算法的有效性。

5 结论

为进一步提高车载SINS/GPS组合导航精度，本文针对卫星信号失效时SINS位置误差随时间积累以及SINS/GPS组合导航中量测噪声协方差矩阵不确定性问题进行了分析与研究。得到以下主要结论：

1)对车辆运动学约束条件进行了研究，研究结果表明卫星信号失效时利用车辆侧向与天向速度为零这一约束条件可以在不增加外部传感器的前提下提高SINS长时间导航精度。

2)为实时获取较为准确的量测噪声协方差矩阵，提出了一种新的FIS-ADKF组合导航融合算法。进行了车载导航验证试验，结果表明速度约束能够抑制SINS位置误差随时间的快速积累，同时本文所提出的FIS-ADKF组合导航融合算法能够提高滤波器状态估计精度。后续研究中将会考虑引入里程计，利用里程计提供的前向速度进一步提高组合导航系统精度，进而实现车载SINS/GPS的高精度组合导航。