前缘钝度对高速翼型颤振边界的影响

郭 力,刘杰平, 吕计男,王昕江,季 辰,刘子强

(1.中国航天空气动力技术研究院, 北京 100074；2. 中国运载火箭技术研究院,北京 100076)

0 引言

为了提高高速飞行器的装载比例,其结构的刚度与质量下降,从而可能引起结构的气动弹性振动问题。针对高速飞行器的气动弹性问题,McNamara等[1]采用NASA Lanley研究中心的CFL3D程序计算了Mach数在2.5～28范围内高速飞行器的控制面与整机的气动弹性问题,并与活塞理论进行了对比,分析了活塞理论与CFD/CSD耦合计算的误差范围。Lamorte等[2]针对高速飞行器的控制面进行了气动弹性计算,考察了真实气体效应、湍流模型、转捩位置对于颤振边界的影响,发现上述效应通过影响热环境,影响气动弹性性能。Ilie等[3-5]采用大涡模拟(LES)方法,对平板及翼型的气动弹性响应问题开展了算例研究。季辰等[6]发展了在高超声速风洞中对结构进行气动弹性实验的方法,研究了钝前缘梯形翼[7]、舵面[8]的气动弹性特性,并获得了梯形舵面的颤振边界。窦怡彬等[9]采用分层求解技术研究了根部固支的高超声速舵面颤振响应和频率。叶坤等[10]也采用分层求解技术分析了全动舵面结构的热边界影响。

国内外学者对于高超声速环境下的舵面气动弹性问题进行了数值、实验探索,所研究的对象具有工程实际意义,但所研究的外形变化较大,较难形成系统性的认识。在高超声速条件下,为了减小高超声速时激波产生的阻力,高速飞行器的舵翼面大多采用尖前缘构型,同时为了降低加热对结构的影响,需要对前缘进行钝化。本文以二维翼型为研究对象,通过变化翼型前缘的钝化程度,探讨单纯的钝度因素对翼型气动弹性性能的影响，为高超声速下翼型前缘钝度对颤振特性的影响研究提供参考。

1 计算模型

本文采用二维翼型作为模型考察高速下不同前缘钝度对颤振边界的影响。本研究采用了3个不同的前缘钝度进行了模拟,如图1所示。第一种为尖前缘构型(图1(a)),此构型在高速来流条件下会在前缘产生斜激波,激波的强度与正激波相比较小,波后的压力增加与热流较小。后两种分别为1/60m半径前缘(图1(b))与1/30m半径前缘构型(图1(c))。这两种构型会在前缘产生较强的正激波,产生的阻力较大。但是此类钝前缘构型,有利于结构的防热设计,在气动加热效应比较明显的高速速度范围能够较好地保持结构的完整性。

(a)

(b)

(c)图1 计算采用的翼型截面形状Fig.1 Illustration of wing sections

计算来流Mach数为5,参考高度为10km。为了得到翼型结构的颤振边界,通过增加来流密度的方法增加动压。在高度10km时，Mach为5，来流空气的动压为7.6×105Pa,为了得到颤振边界,又分别考虑了来流动压为15.1×105Pa、30.2×105Pa、60.5×105Pa这3种工况。通过对这4种情况的考虑,得到了各个来流动压下的时域响应曲线,并根据这些曲线提取阻尼比,通过插值得到阻尼比为0时的动压即为颤振边界。

结构模型如图2所示。翼型结构为刚体,具有沉浮与俯仰两个自由度。翼型的转动中心在翼型的中心,质心在转动中心前0.1m。质量为10kg,转动惯量为14kg·m2,沉浮刚度为2×105N·m,扭转刚度为1×106N·m2。在计算过程中,结构与气动力耦合,在俯仰与沉浮两个自由度上运动。

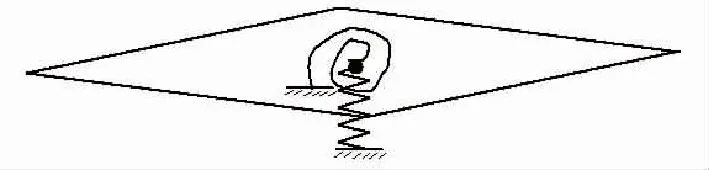
图2 结构模型示意图Fig.2 Illustration of structure model

在实际计算过程中,由于考察的是系统的颤振边界,只需要考虑结构振动的趋势,从中得到振动的阻尼比,所以结构运动的振幅不需要较大,只需要考虑小振幅就可以。根据此小振幅假设,可以将振动的特征向量进行线性化,得到线性的振动幅度,从而对转轴的转动位移进行线性组合运算。翼型的质心在15%弦长处,翼型质量与转动惯量均设为1,由此得到翼型的沉浮与俯仰两阶模态的频率分别为ω1和ω2，如表1所示。

表1 两阶模态的固有频率

2 数值方法

为了方便描述动网格上的流体运动,流场采用积分形式的任意拉格朗日-欧拉(ALE)N-S方程[11]描述,其表达式如下

(1)

(2)

(3)

式(1)～式(3)中，ρ为密度，vi为各个方向的速度，vm,j为各个方向的控制体表面速度，p为压力，E为总能量，T为温度。计算过程中空间离散采用Roe格式,时间推进采用双时间步的LU-SGS方法。

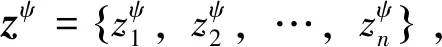
z=ψzψ

(4)

模态坐标的方程为

(5)

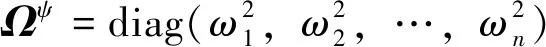
3 颤振分析结果

3.1 流场分析

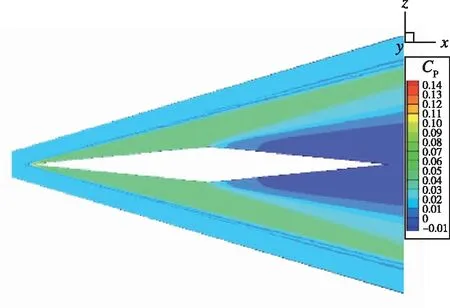
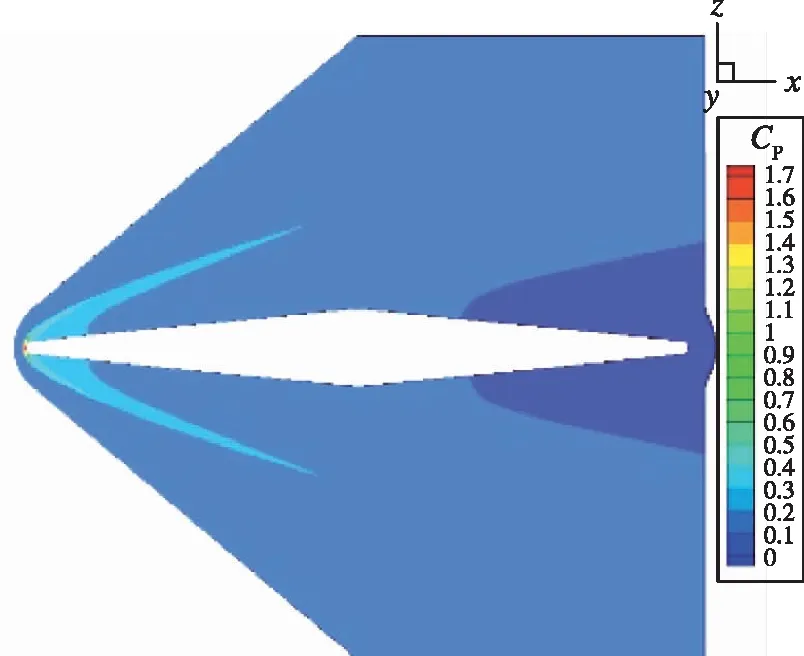
在Mach数为5.0时,各个构型的流场如图3所示。对于尖前缘的翼型,在翼型周围形成了斜激波,激波的倾角由尖前缘的前缘角决定。对于钝前缘的两个截面,在前缘前方形成了弓形激波。前缘钝度的增加,使得前面的弓形激波强度增加,并且后面的斜激波的倾角增加。

(a)

(b)

(c)图3 不同翼型截面与对应的定常流场Fig.3 Flow fields of the 3 wing section shapes

3.2 不同来流动压下的时域数据

计算初始时刻对翼型施加初始速度扰动,通过计算得到其时域响应数据,对得到的时域数据进行分析可以得到系统的阻尼比和特征频率。

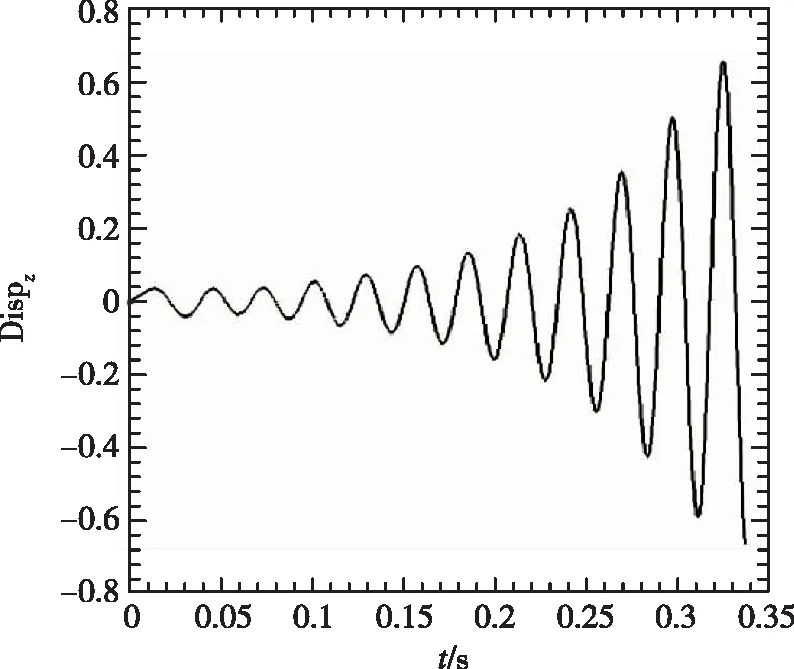
(1) 尖前缘外形变动压得到的时域数据

从图4中看到,随着动压的增加,振动幅度增大,并最终发散。

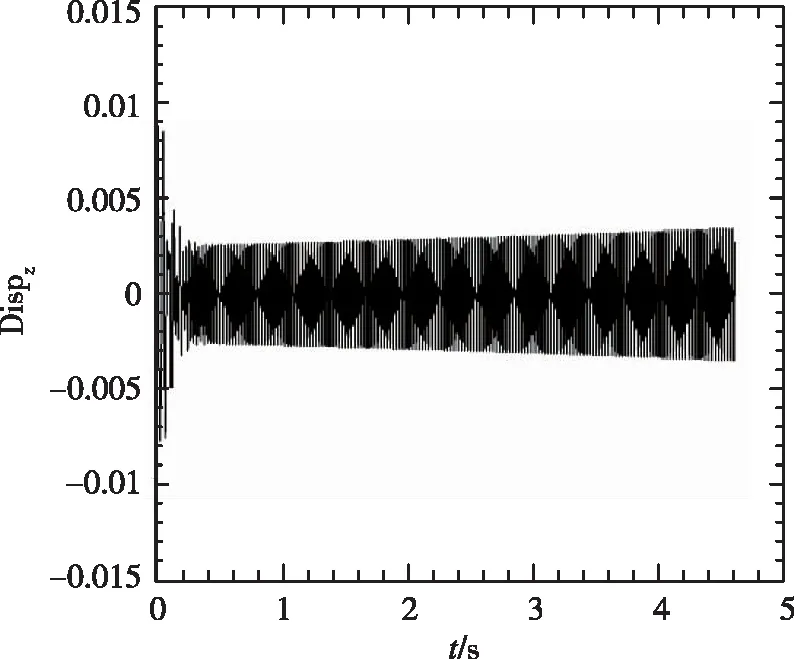
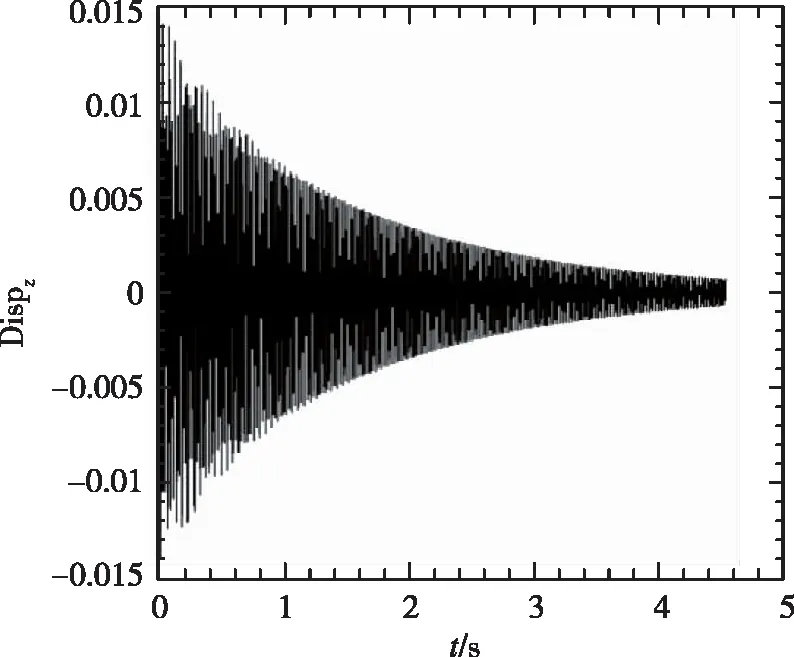
(2) 1/60m半径前缘外形变动压得到的时域数据

从图5中看到,随着动压的增加,振动幅度增大,并最终发散。1/60m半径前缘的时域数据与尖前缘的时域数据相比,从定性角度看到发散较慢。

(a)

(b)

(c)

(d)

(a)

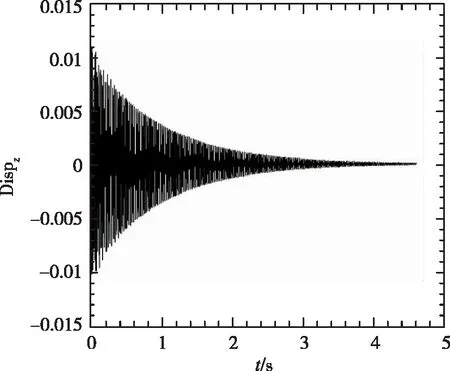
(b)

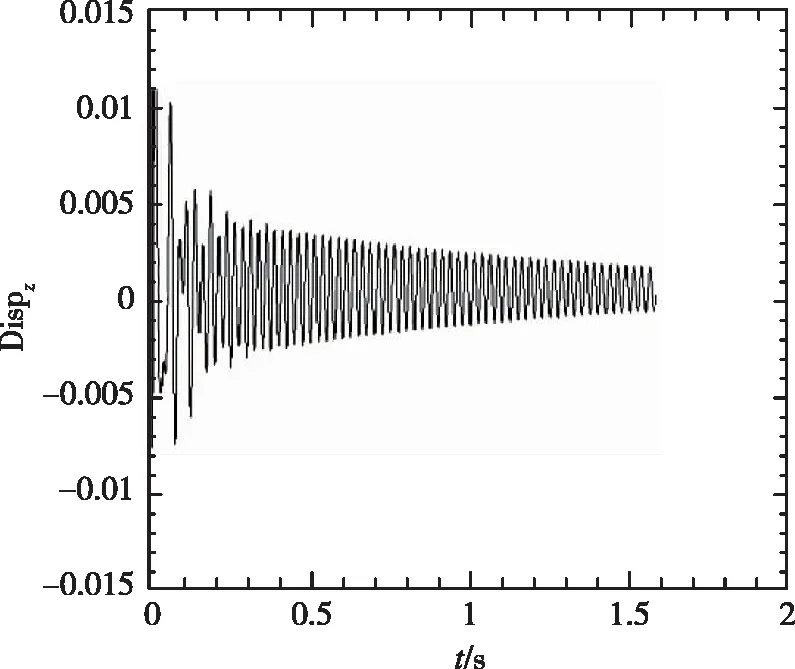
(c)

(d)

(3) 1/30m半径前缘外形变动压得到的时域数据

通过对上面两组计算从定性角度观察,即使对于相同的动压增长趋势,1/60m半径前缘与尖前缘相比发散趋势减小。反映到计算颤振边界上,可以预计,前缘钝度的增加会使得颤振边界增加。为了进一步确认此趋势,更进一步增加了前缘的钝度,采用图1(c)中的翼型进行了颤振计算。计算采用的Mach数与动压增加梯度与前面两组计算相同，并通过固定在翼型前缘的点的位移得到了时域数据。

1/30m半径前缘的计算的时域数据如图6所示,与尖前缘与1/60m半径前缘的计算相比,从定性上看,随着动压的增加,发散的趋势更加不明显,同时在最大动压点时域数据未显示出发散的趋势,而是呈现出等幅振动的趋势。

3.3 颤振频率与阻尼比分析

3.3.1 锐前缘翼型

采用自回归移动平均方法[13](ARMA)对锐前缘翼型前缘的位移时域数据进行了分析,分别得到了不同动压下的频率与阻尼比,如表2所示。时域分析得到的频谱图如图7所示。从频率上可以看出,随着动压的增加,最高频率与最低频率逐渐靠近。在颤振没有发生时,时域数据的频谱分析具有两个峰值,分别对应两个模态的振动频率。当颤振发生时,时域数据发散,此时只有一个对应的频率。

将来流动压表示为阻尼比的函数,则在阻尼比为0时对应的动压为颤振动压。阻尼比与颤振动压的函数关系通过已知的动压-阻尼比数据插值得到。相应的插值曲线与数据点如图8所示。根据此函数关系,得到阻尼比为0时对应的颤振动压为3.01×106Pa。

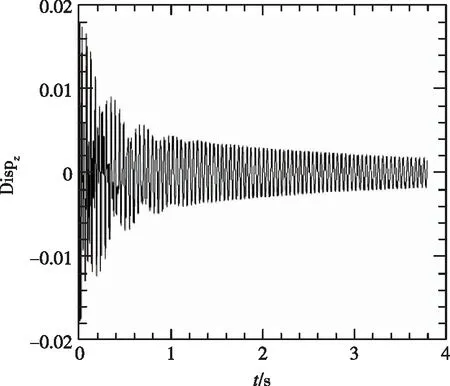
(a)

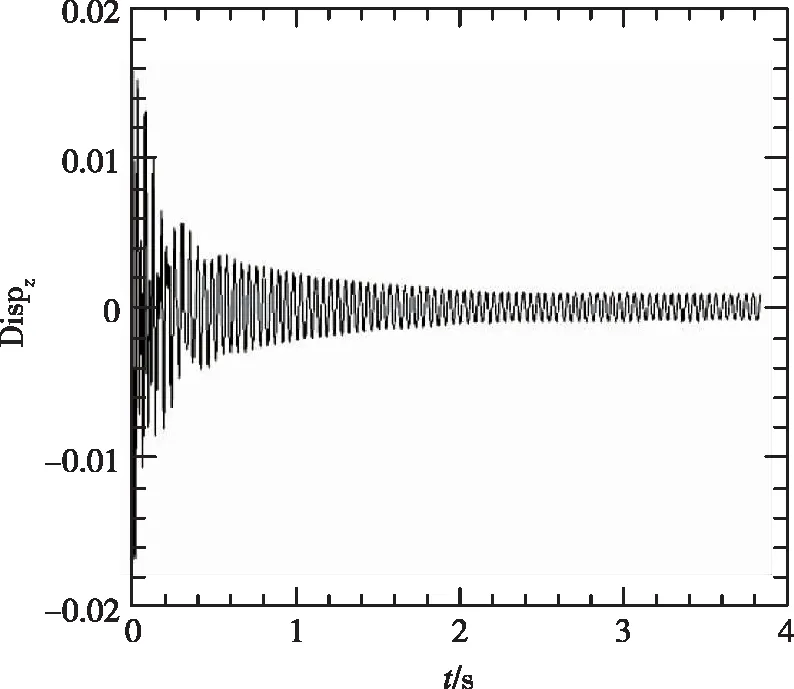
(b)

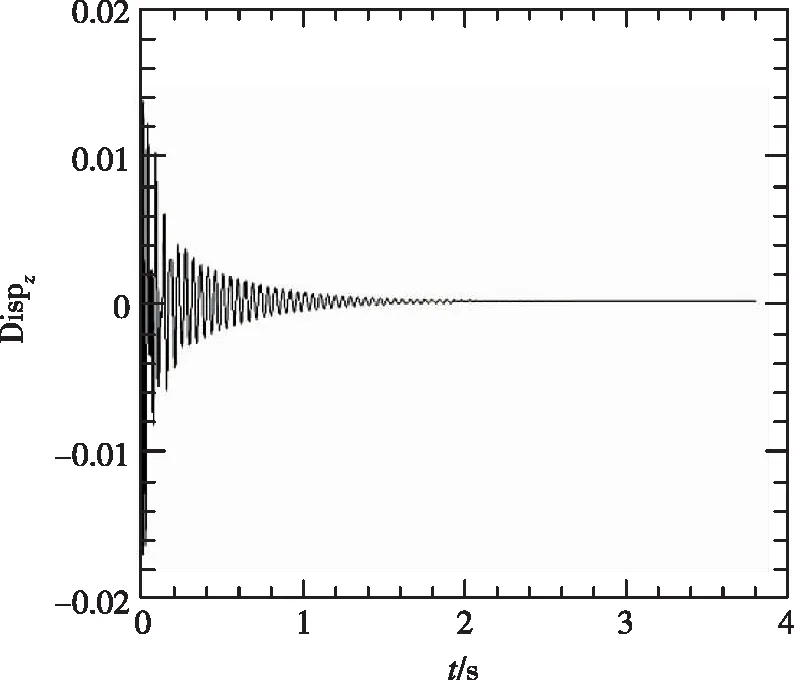
(c)

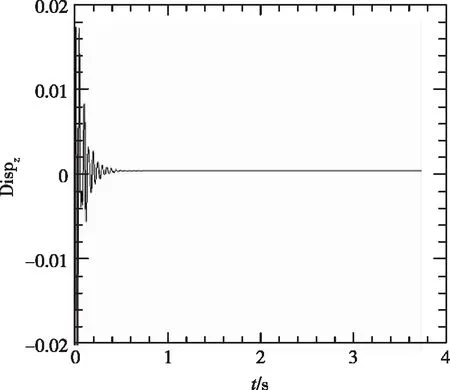
(d)

表2 锐前缘翼型频率与阻尼比

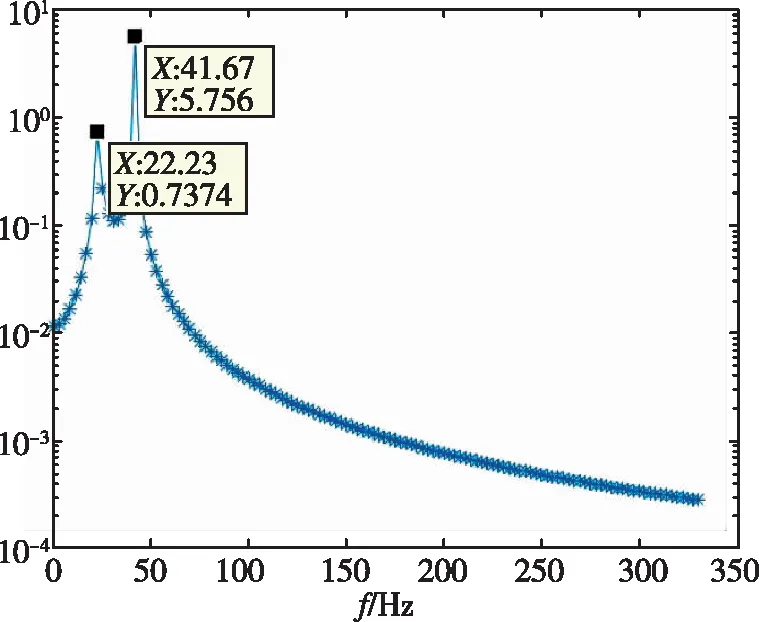
(a)

(b)

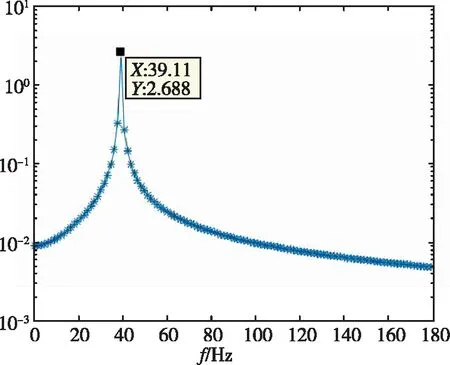
(c)

(d)

图8 锐前缘翼型阻尼比与颤振动压Fig.8 Sharp-edge wing damping ratio vs. incoming flow dynamic pressure

3.3.2 1/60m半径前缘翼型

对1/60m半径前缘翼型前缘的位移时域数据进行分析,分别得到了不同动压下的频率与阻尼比,如表3所示。时域分析得到的频谱图如图9所示。从频率上可以看出,随着动压的增加,最高频率与最低频率逐渐靠近。在颤振没有发生时,时域数据的频谱分析具有两个峰值,分别对应两个模态的振动频率。当颤振发生时,时域数据发散,此时只有一个对应的频率。

表3 1/60m半径前缘翼型频率与阻尼比

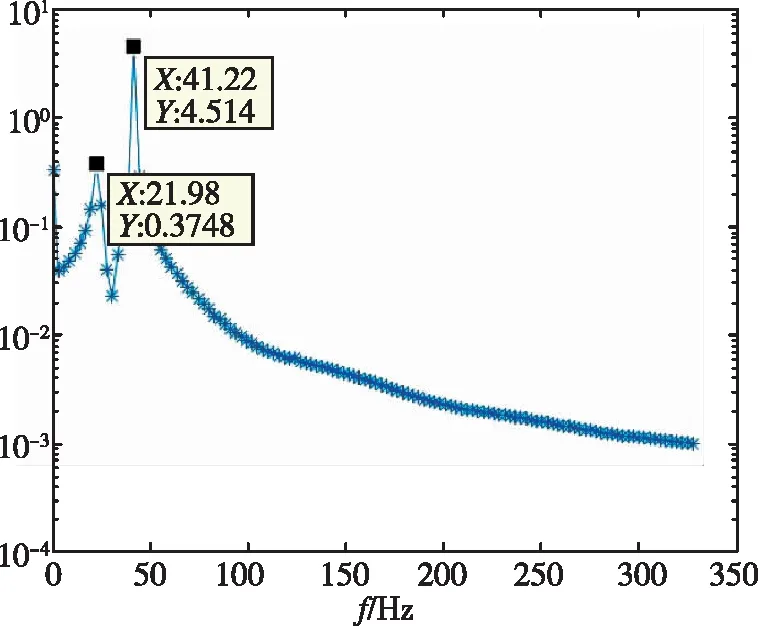
(b)

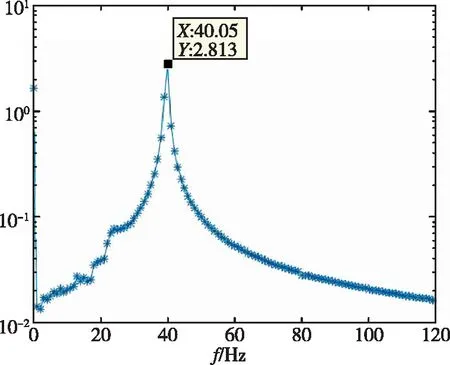
(c)

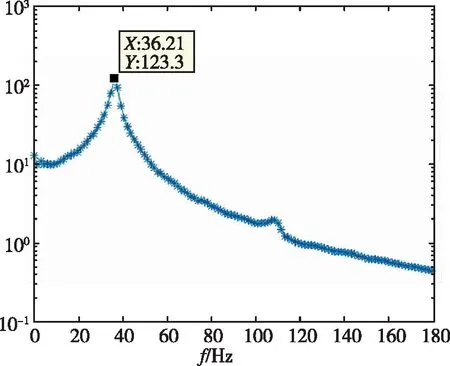
(d)图9 1/60m半径前缘翼型频率分析Fig.9 Frequency of 1/60m blunted-edge wing

将来流动压表示为阻尼比的函数,则在阻尼比为0时对应的动压为颤振动压。阻尼比与颤振动压的函数关系通过已知的动压-阻尼比数据插值得到,相应的插值曲线与数据点如图10所示。根据此函数关系,得到阻尼比为0时对应的颤振动压为3.25×106Pa。

图10 1/60m半径前缘翼型阻尼比与颤振动压Fig.10 1/60m blunted-edge damping ratio vs. incoming flow dynamic pressure

3.3.3 1/30m半径前缘翼型

同样对1/30m半径前缘翼型前缘的位移时域数据进行了分析,分别得到了不同动压下的频率与阻尼比,如表4所示。时域分析得到的频谱图如图11所示。从频率上可以看出,随着动压的增加,最高频率与最低频率逐渐靠近。在颤振没有发生时,时域数据的频谱分析具有两个峰值,分别对应两个模态的振动频率。与锐前缘和1/60m半径前缘算例不同的是,1/30m半径前缘即使在8倍动压的情况下仍没有发散。

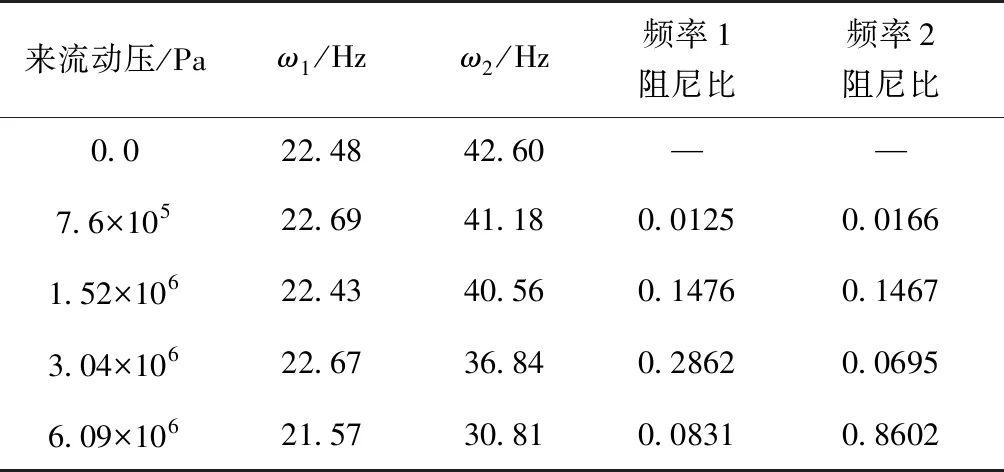
表4 1/30m半径前缘翼型频率与阻尼比

将来流动压表示为阻尼比的函数,相应的数据点如图12所示。可以看出,即使在最大动压状态下,振动仍没有发散,因此1/30m半径前缘的翼型颤振边界高于前面两种构型。虽然在计算设置的动压情况下没有得到结构振动发散,从而没有得到具体的颤振边界数据,但是此结果与前面结果的趋势一致,说明了随着翼型前缘钝度的增加,颤振边界逐渐提高。

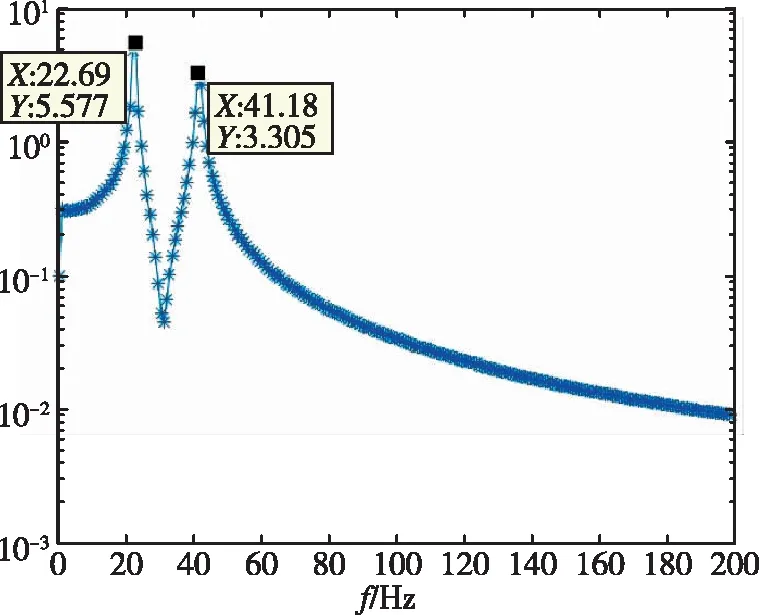
(a)

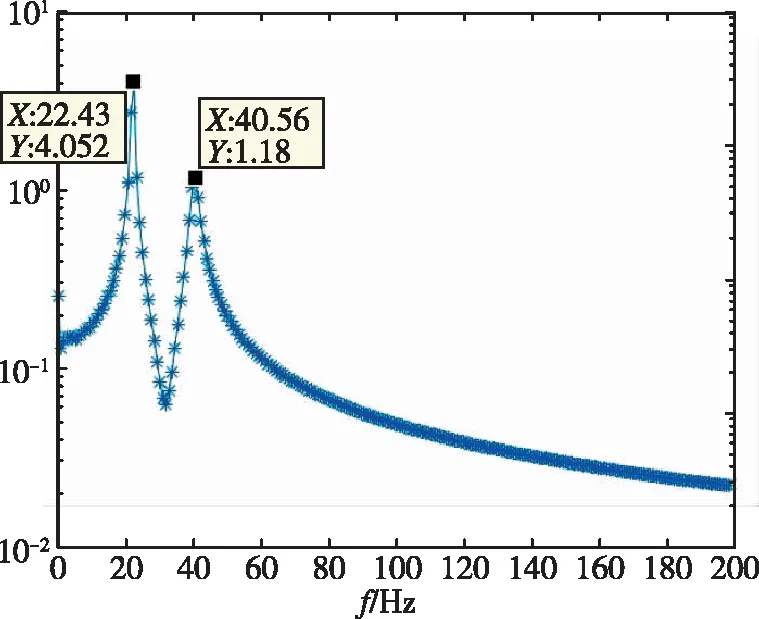
(b)

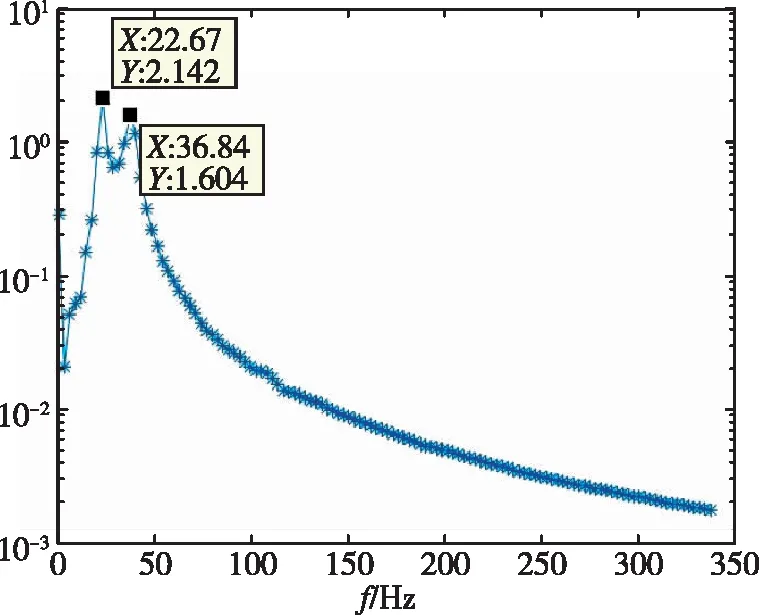
(c)

(d)图11 1/30m半径前缘翼型频率分析Fig.11 Frequency of 1/30m blunted-edge wing

图12 1/30m半径前缘翼型阻尼比与颤振动压Fig.12 1/30m blunted-edge damping ratio vs. incoming flow dynamic pressure

4 结论

根据从锐前缘到1/30m半径前缘的气动弹性分析,发现随着前缘钝度的增加,即使翼型的刚度、质量不发生改变,颤振边界也会不断提高。随着翼型前缘钝度的增加,在高速下,头部激波结构从斜激波转变为脱体的弓形激波。激波结构的变化使得翼型在运动情况下产生的使得翼型发生俯仰运动的力矩发生了变化。而只有翼型在平动过程中产生力矩并与沉浮运动耦合,才会出现翼型结构的自激振动,从而发散出现颤振现象。在锐前缘情况下,力矩较大,随着前缘钝度的增加,翼型上受到的力矩逐渐减小。一个极端的情况为球形,此时如果忽略黏性作用,球形受到的力矩为0。因此,增大前缘钝度可以提高颤振边界。