多自由度仿生扑翼飞行机器人结构设计与分析

王 超,屈方杰,黄恒敬,仲 军

(河海大学机电工程学院,南京 213000)

0 引言

在飞行机器人领域,仿生飞行机器人拥有相较于普遍的四轴飞行器更加美观的外形,并且能模拟鸟类飞行时的启动、悬停和降落时的动作。这类仿生飞行器因为外观与鸟类相似,能更好地在军事、反恐及娱乐等众多领域,发挥侦察、巡逻与教育等积极作用。

早在1973年,Weis-Fogh[1]就针对黄蜂的飞行特性,提出了扑翼飞行的概念,并详细地分析计算了扑翼产生的升力,为飞行领域开创了新的学科分支。

2015年，Yang等[2]在仿生扑翼飞行器原理的设计与研究中,对扑翼机器人的具体设计步骤做了详细的介绍。在设计扑动机构的主体时,采用了被普遍使用的扑翼机构,并且在该机构的基础上加了一个用于模拟鸟类内外部肌肉交替收缩的平行机构,并对机构进行UG建模、ADAMS和Fluent的仿真分析,最后对机翼和尾部形状进行仿生设计。

2015年，潘尔振[3]结合海鸥的功能和性能指标,通过结构设计和样机选型等过程,设计出具有一个自由度的扑翼机器人,并开发了一套实验装置测试结构合理性等性能指标,最后基于数据对结构进行优化设计。

2016年，阮龙欢[4]对扑翼飞行机器人的应用背景和技术做了深入的分析和研究,并设计一种类似蜂鸟扑动的扑动-扭转两自由度耦合驱动机构,在ADAMS软件中建立了基于该机构的虚拟样机,并分析了虚拟样机的基本运动特性。

在仿生扑翼飞行器的研究上,国外的研究起步早,技术暂时还领先于国内。随着国内各大高校、实验室以及飞行器爱好者对于扑翼飞行的关注,已经有不少学者取得不错的成绩，但研制成功的飞行器大多数还是单自由度,无法达到真正模仿鸟类飞行和大范围普及推广的程度,距离世界领先技术还有不少的差距。归根结底是因为仿生飞行机器人相较于市面上的普通飞行器,存在设计复杂、控制复杂的问题,并且现有的研究仿生程度不高,运动学和动力学领域对于扑翼结构的建模分析还有待深入探讨和研究,智能控制系统还有待进一步开发和完善[5-10]。大型扑翼飞行机器人结构研究对于开发多自由度仿生扑翼飞行器在理论和实际应用上都具有很强的研究价值[11-14]。

本文旨在对大型的扑翼飞行机器人的结构进行研究。由于多自由度仿生扑翼飞行器在飞行时的频率较低,所以在每次扑动时要求的升力和推动力比螺旋式飞行器大,因此,精妙的扑翼传动是结构设计中的关键问题。在理论的结构设计后,还需要对设计出的结构进行动态构件计算分析、运动学计算分析、建模仿真等,以提高设计的准确性和可行性。

1 结构设计

1.1 海鸥飞行方式与运动规律分析

翅膀是海鸥能够飞行的主要身体部分,轻质且坚韧的羽毛和骨骼在扑动的过程中产生飞行所需要的升力。海鸥的羽毛大致分为覆羽和飞羽两类，如图1所示。覆羽排列密且短,飞羽排列稀疏但长。海鸥的飞行主要由起飞阶段、巡航阶段、转向、降落阶段组成。

海鸥在巡航过程中,翅部有4个基本的扑动动作：下行程、折叠过程、上行程、伸展阶段。这4个动作可以大致看做一个完整的拍打过程。翅膀在下行程前的伸展阶段需要尽可能大地展开,这样翼展和升力面积才能达到最大值,并在下行程阶段产生所需的大部分升力。上行阶段是被动回复的过程,并且行程需要的时间很短。在这个阶段之前,翅膀折叠,目的是缩短翼展和减少阻力。在上行程中,空气阻力会急剧增大。如果鸟类能在这个时候折叠翅膀,可以减少有效的作用风区,从而大大减少空气阻力[15]。

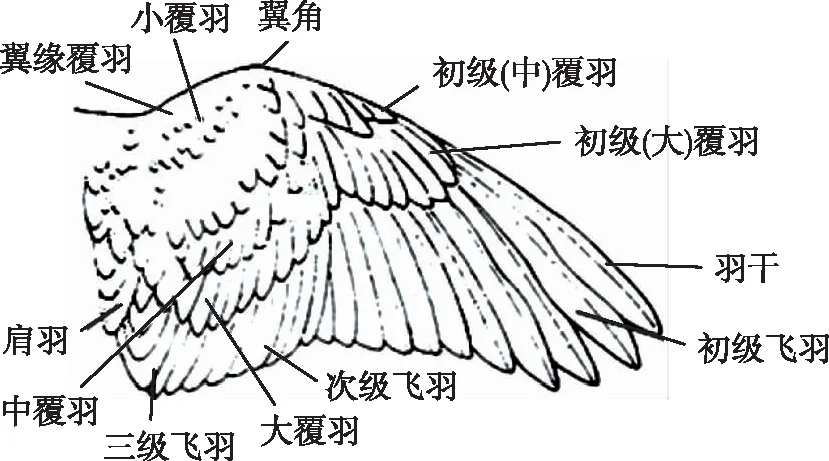
图1 鸟类翅膀示意图Fig.1 Schematic diagram of bird wings

海鸥一类的大型鸟类主要扑动飞行的频率比较低。在巡航过程中,因为翼展大小决定了扑动频率,海鸥的扑动频率大约为5Hz,最低的时候只有1Hz～2Hz[16]。

根据观察发现,在海鸥的一个拍打过程中,不仅翅部上下扑动,而且根据上下形成的空气阻力不同,翅膀还会有小幅度的接近线性扭转,翅尖部分扭转幅度最大,越靠近身体方向扭转幅度越低。

海鸥在巡航飞行过程时,一对翅膀的运动是完全左右对称的,这样的运动有利于海鸥在大型的风浪面前保持身体的平衡和对抗气流飞行,例如Festo公司研制的一款Smartbird[17]仿生海鸥机器人,其运动典型动作如图2所示。

图2 Festo公司Smartbird仿生海鸥Fig.2 Festo’s Smartbird bionic seagull

1.2 仿海鸥扑翼飞行机器人结构设计

1.2.1 整体结构设计

设计的要求是需要满足仿海鸥飞行特点和产生足够的升力维持飞行，以及在外形上与海鸥相似。使用SolidWorks软件设计结构,生成三维模型可以更加直观地修改和完善结构设计。

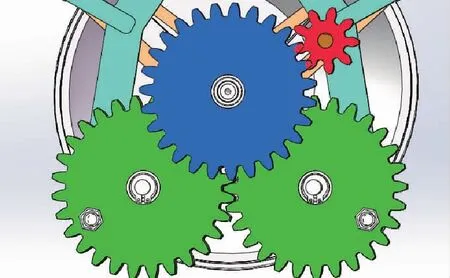
图3 传动部件局部图Fig.3 Partial view of transmission components

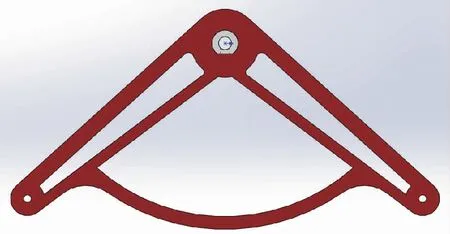
图4 前支骨架零件图Fig.4 Front support skeleton parts

图5 螺栓连接剖视图Fig.5 Sectional view of bolted connections

图6 最终装配效果和海鸥对比图Fig.6 Comparison of final assembly effect and seagull

1.2.2 扑翼结构设计

翅膀翼型骨架的设计上,参考美国NACA系列翼形,选择了具有较好气动特性的弧形机翼,再根据前文所确定的翼展投影面积,设计出的翅膀翼型骨架如图7所示。镂空的设计既保证飞行时所需要维持形状的强度,也减轻了零件的质量,同时根据仿生学和流体力学的研究成果,一边翅膀有8个翼型骨架,从机身向外到最后一个翼型骨架,每个骨架的形状和尺寸都略有差异,翼型骨架的前沿的小孔和后沿都将与钢丝串接在一起,这样在末端翼型骨架被施加扭力时,其他骨架也会随之扭动。这样的设计模拟了海鸥在不同空气阻力时,翅膀会有小幅度的接近线性扭转,翅尖部分扭转幅度最大,向身体方向扭转幅度递减。

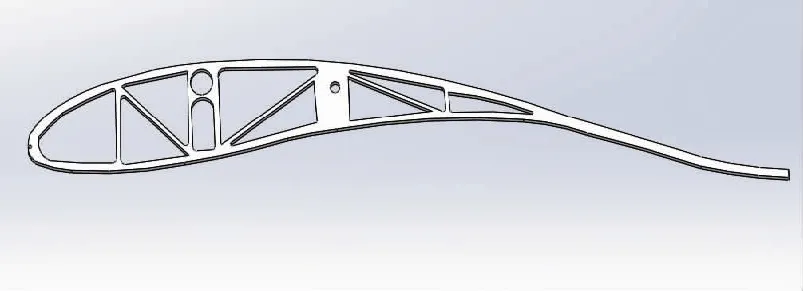
图7 翅膀翼型骨架Fig.7 Skeleton of wing airfoil

机尾部还加装了微型舵机和控制器用于飞行过程中为获得最佳飞行效率而将翅膀轴向扭动。

扑翼结构采用的是两段式的翅型,即拍打过程中带有折叠过程。靠近仿生海鸥身体的一段翅膀称为主翼,远离身体的一段翅膀称为副翼。鸟翼的结构十分精巧,想要完全真实的模仿对于现在的技术而言是十分困难的。所以主、副翼结构的设计主要需要满足：1)翅膀的上下拍打运动；2)翅膀下行程时主翼和副翼向外舒展；3)翅膀上行程时主、副翼折叠。根据上述设计需求,提出了传动效率高且结构简单可靠的机构设计,机构简图如图8所示。

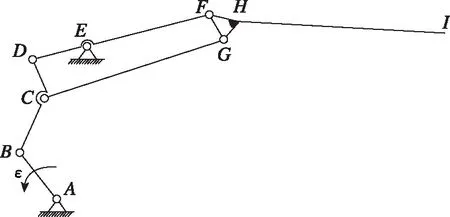
图8 主翼和副翼机构简图Fig.8 Schematic diagram of main wing and aileron mechanisms

从图8中可以看出,杆件AB是一个曲柄,与杆件BCD铰接一起,带动主翼杆件DF和CG,在杆件加入固定件E,使机构固定位置的同时达到上下扑动的设计要求；连接件FHG加入一段连接主翼杆件DF和CG,另一端采用固定连接副翼杆件HI,连接件FHG的另一个设计作用使主翼在下行程中副翼杆件向外舒展,主翼在上行程中副翼相对向相反方向运动,达到相对主翼折叠的效果,这样能最大效率地减小空气阻力，实现功率的最大化；∠BCD的大小和CD的长度都经过试验确定，以确保其在运动时满足下行程时主翼和副翼向外舒展、上行程时主翼和副翼折叠的设计要求。

1.2.3 传动结构设计

因为要使两端的翅膀完全对称运动,所以传动设计选择了精准度较高、需要在频繁且重复的工况下有较为优异的稳定性、运用较为广泛的直齿轮传动。在传动装置中还设计了二级减速装置,使最终输出装置的转速大幅减小。根据以上目标所得设计方案,如图9所示。

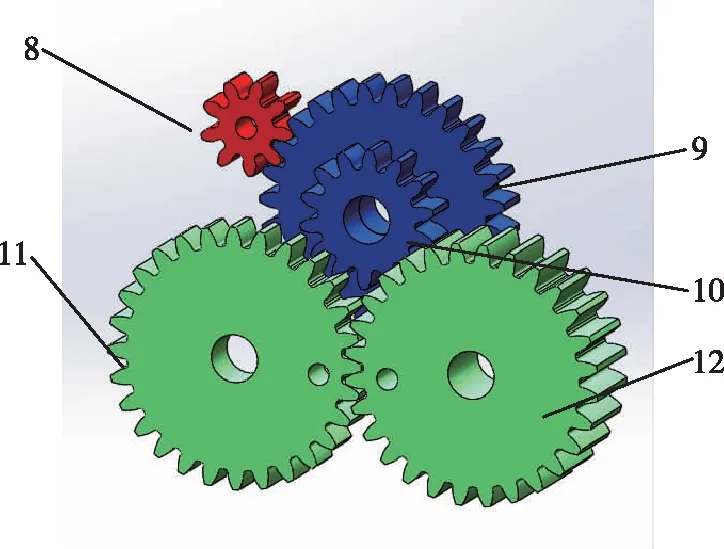
图9 传动齿轮设计Fig.9 Transmission gear design

传动装置中设计了二级减速装置如图9所示,其中所有齿轮的模数都为m=2,齿轮8为主动齿轮,齿数为9,通过与电机连接带动整个齿轮副转动。齿轮9(齿数为27)与主动齿轮8外啮合,与齿轮10(齿数为14)同轴固定,目的是使齿轮9和齿轮10以同一角速度旋转,同时小齿轮8为主动齿轮啮合齿数较大的齿轮9可以达到减速增扭矩的效果。齿轮8、9、10组成了一个二级减速传动齿轮副,达到降低转速、增加扭矩的目的。齿轮11和齿轮12在其上打孔并在后期加装在扑动机构上,目的是充当扑动主、副翼的两个曲柄。齿轮11和齿轮12模数和齿数都相同,外啮合达到两侧翅膀完全对称运动的目的,齿轮12较厚,后部与齿轮10啮合。整个齿轮副依据机械装配的原理,通过机身的杆件和轴承与机身进行轴向和径向的固定。

1.2.4 头部和尾部结构设计

结合三点弯曲试验的特点，采用对接的钎焊接头形式，硬质合金放在Cr12钢上，中间为CuMnCo钎料，并用Mo丝控制钎缝的宽度。

通过对海鸥的仿生学和运动学研究了解其飞行特点,在海鸥转向、起飞和降落的过程中,头部和尾部都有参与运动,并且头尾的作用在这些动作的过程中举足轻重。以海鸥飞行过程中转弯为例,首先海鸥会调整双翼的扑动幅度和频率,同时摆头和甩尾控制身体平衡,这样通过翅膀两侧不同的推力和升力差来达到转向的目的。

由于头部在飞行中只起到转向的作用,所以在设计时只考虑流线型线条形状,设计模型如图10所示。有一定弧度的尾部可以在飞行时提供部分一定的升力和推力,所以为了弥补不能做到双翼不同频率扑动所带来的部分飞行灵活性缺失,将尾部的形状设计符合空气动力学原理,如图11所示。头部和尾部中心位于同一根轴线上,通过中心杆件两端与头尾部的操纵圈的球铰链铰接,可以各个方向运动并灵活承受来自各翼面的压力。

图10 头部机构设计Fig.10 Head mechanism design

图11 尾部机构设计Fig.11 Tail mechanism design

头部和尾部分别通过两根钢丝与机身较靠后的两个控制器相连,这个控制首尾部的控制器又称为舵机,如图12所示。舵机通过与控制器相连输出扭力带动操作杆,操纵杆连接钢丝控制头部和尾部,钢丝一侧张紧一侧放松,连接钢丝张紧的一侧就会向内回缩；两侧的钢丝都放松时,该侧零件就会相对身体向下；两侧钢丝都张紧,该侧零件就会相对身体向上。仿生学在观察海鸥运动时发现，海鸥的头部和尾部的朝向总是相反的,所以在设计时需用到两个舵机,每一个舵机都有两个控制杆,分别控制来自头部和尾部的钢丝的松紧,有效地保持整个身躯的平衡。

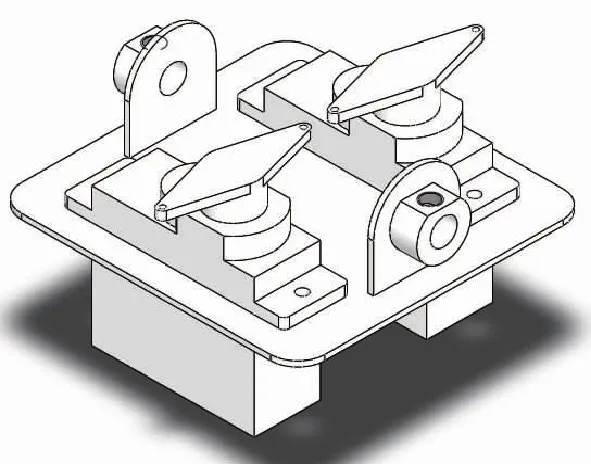
图12 舵机机构设计Fig.12 Design of steering gear mechanism

2 运动学及仿真

2.1 运动学建模

扑翼机构采用双曲柄双摇杆机构,产生两侧为完全对称的运动,故在运动学建模时,仅分析单侧扑翼机构的扑动情况,之后可以由此结论推导出双翼的运动规律。

根据设计的结构,用Visio软件将扑动机构的右半部分的机构简图画出,如图13所示。对该结构进行运动学建模需要运用坐标法和矢量法,所以在这里将A点作为整个扑动结构笛卡尔坐标系中的原点,即坐标点A(0,0)。各杆件的长度以及固定点E点坐标皆为已知量。lAB=20,lBC=65,lCD=16.55,lDE=55,lDF=355,lCG=343.39,lGF=22,lFH=23.26,lGH=30.84,lHI=384,lBD=80.30,∠BCD=155°,∠FHI=154.54°,坐标点E(47.55, 95.57)。设定杆AB为主动旋转部件,转动角速度为ω(单位为rad/s),假设杆件AB与x轴正方向所成的角度为θ1,故由角位移方程可以易知θ1=ωt,所以点B的坐标是一个有关于时间的关系式,即B(lABcosωt,lABsinωt)。

连接BD、BE已在图13上标出。在笛卡尔坐标系内,假设BE与x轴正方向之间的夹角为β,β∈(0,π),BD与x轴正方向的夹角为θ2,θ2∈(0,π),当0<θ2<π/2 时翅膀处于上行程,当π/2<θ2<π 时，翅膀处于下行程。因为点E也是一个关于坐标系固定的点,所以假设EF段与x轴正方向的夹角为θ3,θ3∈(0,π/2)。

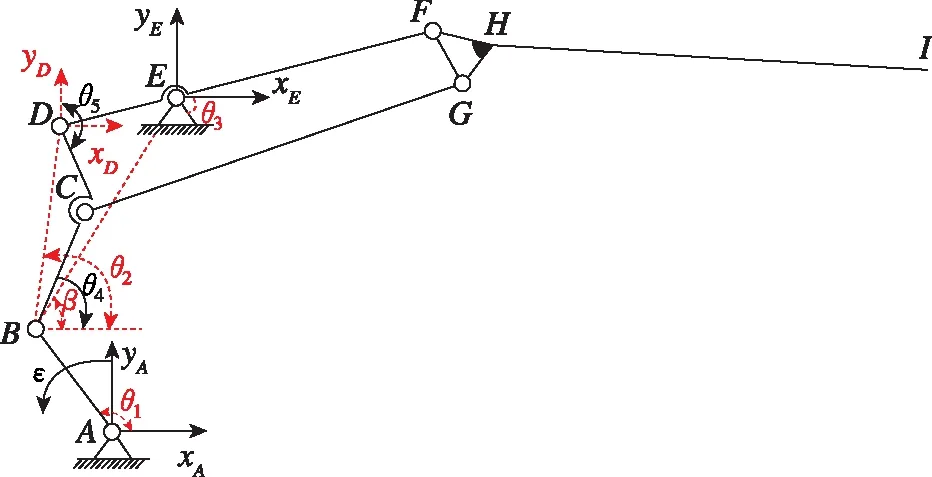
图13 右侧扑翼机构简图Fig.13 Schematic of the flapping wing mechanism on the right

关于坐标点D(xD,yD),根据其位置的三角函数关系,可得

(1)

角度β、∠DBE、θ2和θ3都可由各杆件的位置和特征长度,经过三角函数的变换所得

(2)

(3)

θ2=β+∠DBE

(4)

(5)

关于坐标点F(xF,yF),可通过位置关系得

(6)

坐标点C(xC,yC)是杆件BCD上的点,根据杆组关系式易知

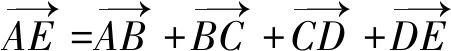
(7)

已知B、D点的坐标,将式(7)的矢量关系式分解成两个相关的坐标关系式

(8)

式中，θ4是水平方向正方向与BD连线之间的夹角,θ5是Y轴正方向与杆件DC之间的较小的夹角。θ4和θ5之间存在的关系式如下

∠BCD=θ4+θ5

(9)

根据式(8)和式(9)可容易求出θ4和θ5关于时间t的关联式,将关联式带入式(8)即可得到坐标点C的关联式。

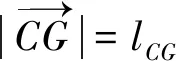
(10)

同理,可得F点坐标(xF,yF)

(11)

在得到坐标点F和坐标点G的关系式后,可以通过余弦定理可以计算出lFI的长度

(12)

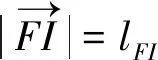
(13)

为了方便计算,将运动学建模所建立的所有公式导入MATLAB进行计算,最后通过式(13)推导出扑翼边缘,即坐标点I关于角速度ω和时间t的坐标表达式,暂时取角速度ω=8rad/s,取坐标点I在运动一个周期内每间隔0.01s时的坐标汇总,在Excel中导入并画出各点连线出副翼尾部在一个周期内的运动轨迹,所得的运动轨迹图像如图14所示。

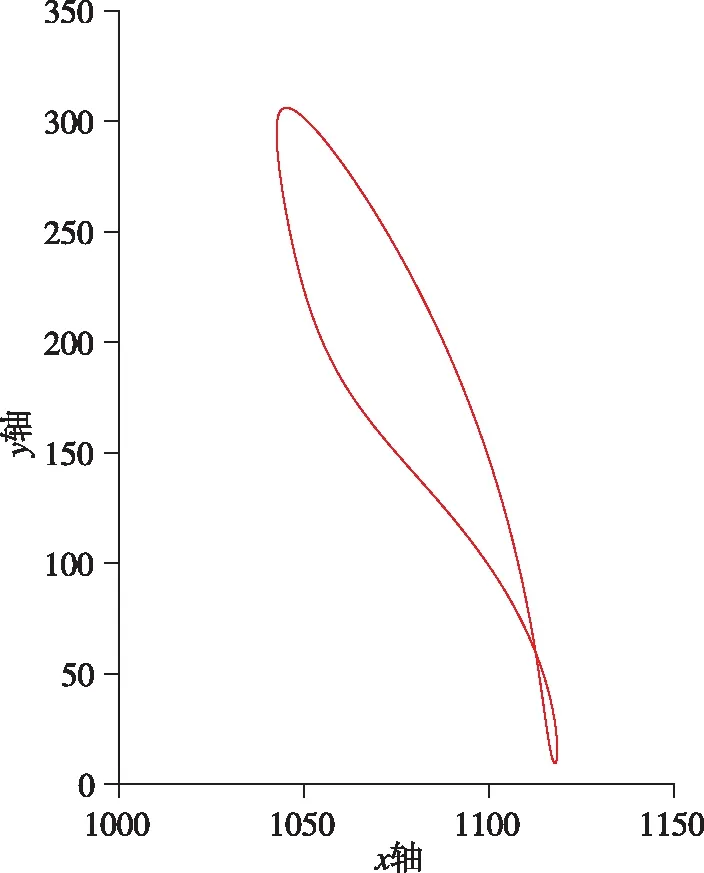
图14 坐标点I运动轨迹Fig.14 Coordinate point I motion curve

2.2 模型仿真

在进行动力学电脑模型仿真之前,首先需要把在SolidWorks软件内建立的所有零件模型进行整合和装配。装配要求符合实际情况,并且需要设定固定数值的驱动力和运动限制,最后将模型的运动方式模拟出来,画出翅膀模型的边缘运动曲线,最后将曲线导出与理论分析结果进行对比。

扑翼飞行结构最主要的部分就是扑翼结构,为了避免其他零件对模拟产生的不可预计的影响以及减少计算量,将模型的其他零件进行压缩,仅留下主要的扑动零件,如图15所示。运用SolidWorks内部运动学仿真插件Motion,对扑翼构件的运动方式做一个设定。在运动算例中首先插入一个旋转马达,根据上文提到海鸥在巡航飞行时的扑动频率为5Hz左右,设置马达为逆时针旋转方向,等速300r/m旋转,马达带动最小的主动轮旋转,具体设置如图16所示。接着对该运动算例进行分析,插入一个翅膀边缘点,对该点进行路径分析。

图15 运动仿真简化模型Fig.15 Simplified model of motion simulation

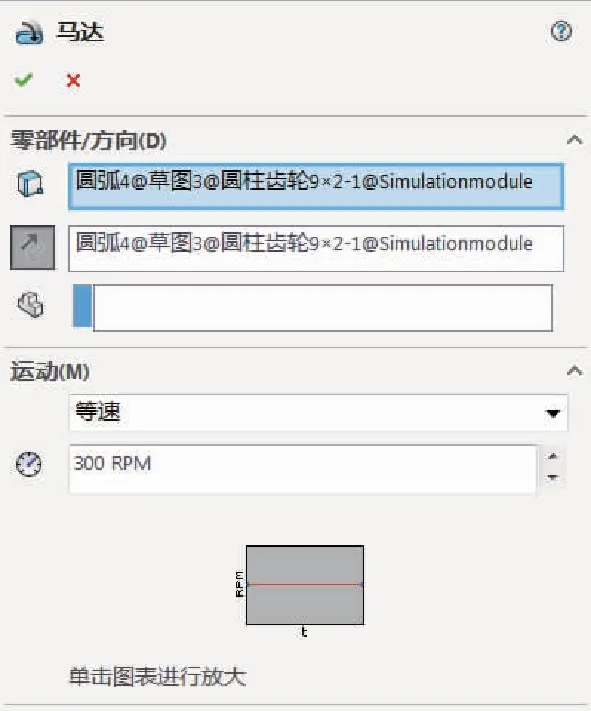
图16 旋转马达设置Fig.16 Rotary motor settings

计算出的副翼末端的位移位置曲线为近似余弦曲线,如图17所示。同时还计算出了该点的线性速度和线性加速度随时间的变化,分别如图18、图19所示。

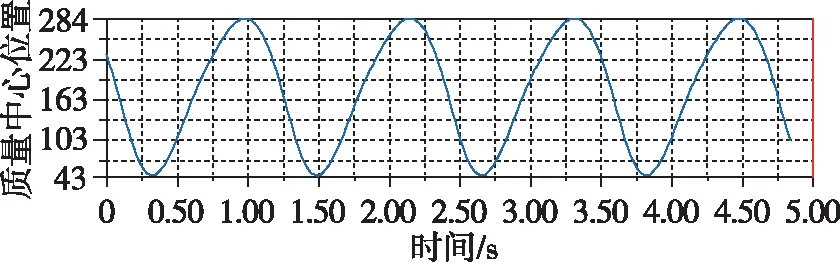
图17 副翼位移曲线Fig.17 Aileron displacement curve

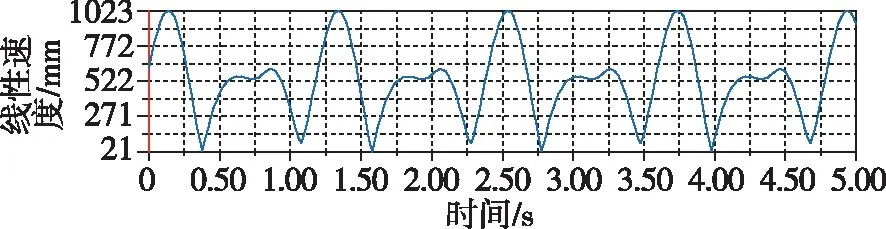
图18 副翼线性速度曲线Fig.18 Aileron linear velocity curve

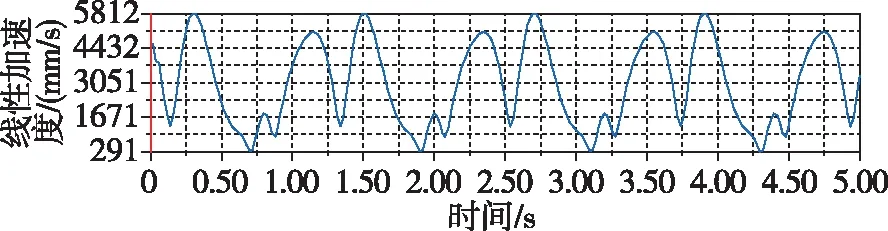
图19 副翼加速度曲线Fig.19 Aileron acceleration curve

取副翼尾部最末端的点在运动时每间隔0.01s的坐标点,将所得的数据导入Excel并作图,生成扑动路径曲线,如图20所示。

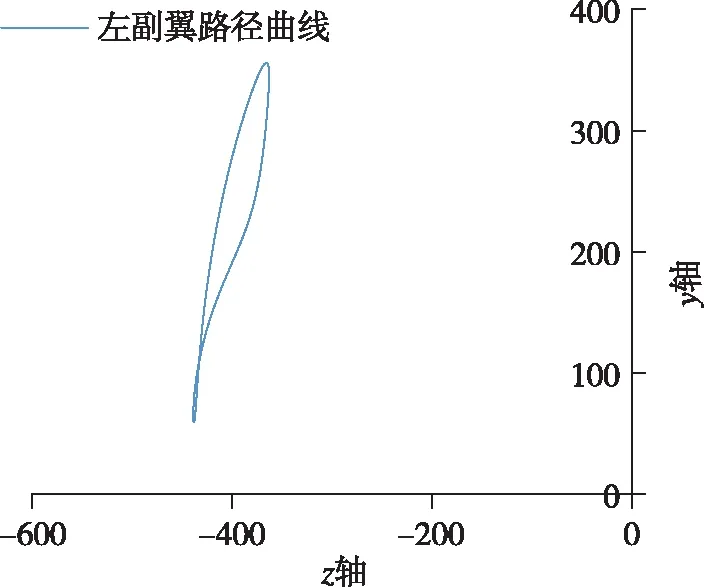
图20 扑动路径Fig.20 Flap path curve

本文同时也对主翼杆件的位置、线性速度以及线性加速度进行了分析,分析所得曲线如图21～图23所示。

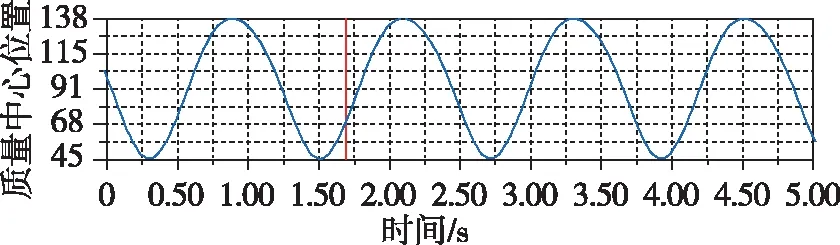
图21 主翼位移曲线Fig.21 Main wing displacement curve

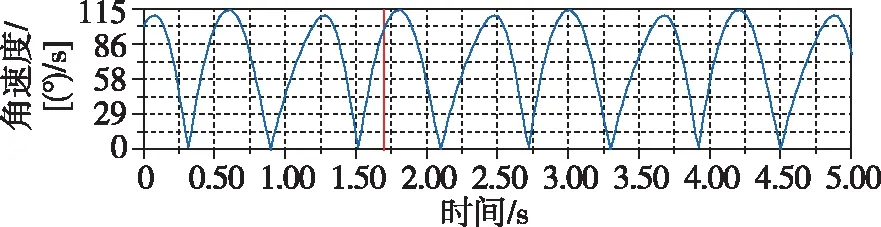
图22 主翼线性速度曲线Fig.22 Linear velocity curve of main wing

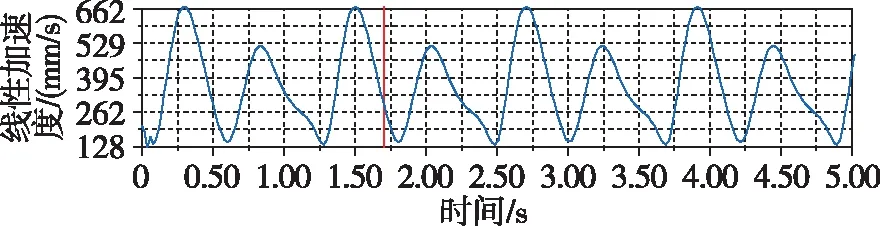
图23 主翼线性加速度曲线Fig.23 Linear acceleration curve of main wing

通过对模型进行建模分析和研究,可以清晰看出所设计的结构运动性能完全符合海鸥的运动特征。副翼翅膀在下行程时,由于空气阻力的作用,速度先快后慢,很好地将动能转化为飞行时所需的升力。而在上行程时由于设计的曲柄具有急回特性以及扑翼的折叠运动,翅膀在行程内虽然受到空气阻力,但是由于机构特性受力面较小,所以加速度有明显的上升。主翼翅膀的运动过程比副翼翅膀更为简单,位移曲线更趋近于正弦曲线,速度也十分平稳,只在运动方向改变时有速度的突变,加速度方面也是在翅膀下行程时较大,能更好地、更高效地为飞行提供足够的升力。从主翼和副翼的速度对比中可以看出，副翼最大速度约是主翼的10倍,设计效果优良。从扑动路径上可以看出，副翼在下行程时具有伸展动作,上下扑动的曲线接近“8”字型,成功模拟了海鸥翅膀的扑动路径规律,在辅以轴向副翼后,扭转时能很好地节省部分功率,十分符合理论计算的预期。

3 结论

本文对扑翼机器人结构进行了研究,通过对相关文献和科研成果进行整理和分析,对多自由度扑翼飞行机器人结构进行设计和分析,从结构设计、运动学分析、建模和仿真模拟等角度开展研究并取得了一些成果。

从仿生学角度出发,在分析了海鸥的飞行特征后,结合目前较为流行的扑翼结构设计,提出了一种具有折翼过程的扑动机构。在整体模型的基础上完善了扑翼机构、传动机构以及头部和尾部的设计。将设计好的数学模型进行运动学的理论分析,证明了设计的机构具有急回特性,采用SolidWorks软件将建立的所有模型结构根据实际要求进行装配,实现了运动模拟。在软件内Motion的仿真结果与理论分析结果基本吻合,证明了设计结构的合理性和可行性。