基于改进蚁狮算法的广义预测控制对T-S 模糊模型的控制研究

张文彬

（上海电力大学自动化工程学院，上海200090）

0 引言

Takagi-Sugeno（T-S）模糊是由日本学者于1985 年提出的[1]，并已经被证明可以任意精度逼近非线性模型，目前已被广泛应用于各个领域。T-S 模糊模型与传统的Mamdani 模糊模型的区别在于其后件是输入量的组合，是确定的值而不是模糊语言。该方法的本质是通过许多小线段来表示非线性系统，从而实现对非线性系统的建模。

蚁狮算法（Ant Lion Optimization，ALO）是模仿自然界中蚁狮捕捉蚂蚁的行为而提出的算法，是近年来新的群智能算法。由蚂蚁的走动来探索解空间，而蚁狮代表了局部最优解，并设下陷阱，来捕捉位置更优的蚂蚁。蚁狮算法的最大优点在于其所需要的人为给定的参数少，并且容易实现。自2015 年被提出以来[2]，就受到了广泛的关注，对该算法的改进也在不断地探索之中。

广义预测控制自1987 年提出以来，凭借其优良的控制效果受到了广泛的关注，其对象大多为受控自回归积分滑动平均模型（CARIMA）。其作为预测控制算法同样具备预测模型、滚动优化和反馈校正的特点。

1 广义预测控制

广义预测控制的对象常用以下的CARIMA 模型来描述[3]。

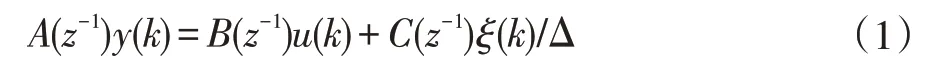
式中y（k），u（k）分别是对象的输出和输入，ξ（k）是噪声扰动，为了简单运算常常设C（z-1）=1。广义预测控制的控制器目标函数如下式所示。

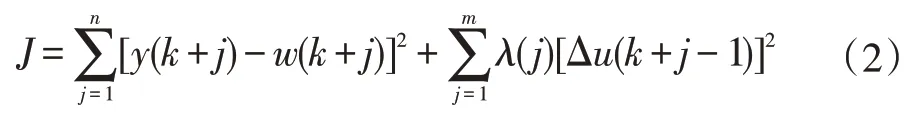
其中λ（j）是加权常数；w（k+j）是输出参考轨迹，其可由式（2）表示。

其中yr是设定值，a 是柔化因子。

为了求得预测输出y（k+j），通过引入以下丢番图方程：

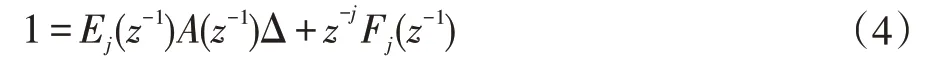
其中的多项式Ej，Fj是由步长j 和模型参数共同决定，表示为：

设Gj(z-1)=Ej(z-1)Bj(z-1)，同时忽略不可测的噪声项的干扰得到的预测输出表达式如下所示。

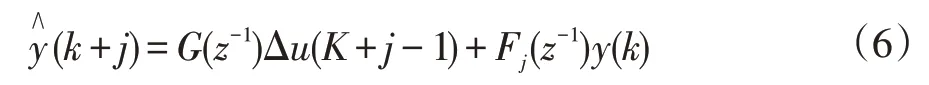
令W=[w(k+1),w(k+2),...,w(k+n)]T，那么目标函数就可以表示为：

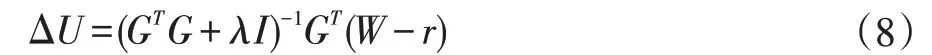
其中r=HΔu(k)+Fy(k)，实际应用时只要将（GTG+λI）-1GT的第一行gT用于控制系统即可，即：

2 蚁狮算法及改进

2.1 基本蚁狮算法

蚁狮算法中由蚁狮、蚂蚁和精英蚁狮组成，其中精英蚁狮有着最优的适应度，代表了全局最优解。算法的基本流程如下：

（1）种群的初始化

随机初始化蚂蚁和蚁狮的位置，并根据适应度大小选择蚁狮中最优的个体作为精英蚁狮。

（2）蚂蚁的随机游走

在迭代开始后，首先根据轮盘赌的方式选择一只蚁狮，每只蚂蚁在其选择的蚁狮和精英蚁狮的周围进行游走。其游走位置可以有下式表示[4]：

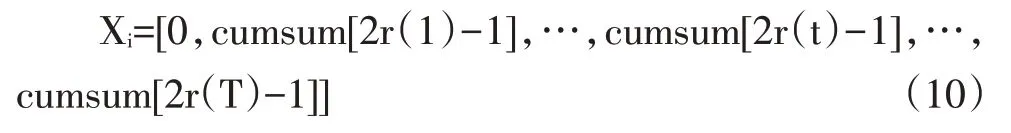
其中t 和T 分别为当前迭代次数和最大迭代次数，r（t）的值为0 或1 可定义为：

对蚂蚁的位置进行标准化以确保其在解空间内进行的游走，具体表示为：

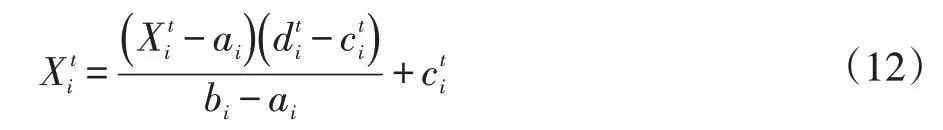
其中ai，bi分别为第i 个变量的下限和上限分别为第t 次迭代时第i 个变量的下限和上限，同时受到被选择的蚁狮的位置影响如式（13）所示。

其中ct，dt模仿蚂蚁落入蚁狮的陷阱后，蚁狮向外刨土，最终使蚂蚁进入穴底的过程。算法通过减小蚂蚁的游走范围来体现，具体为：

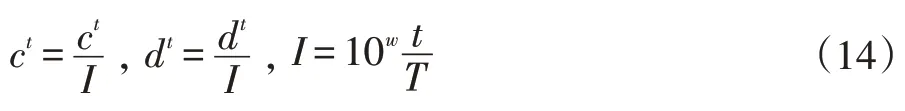
w 的值随着迭代次数的增加而增大，具体为当t＞0.1T 时，w=2；t＞0.5T 时，w=3；t＞0.75T 时，w=4；t＞0.9T时，w=5；t＞0.95T 时，w=6 最终蚂蚁的位置可以表示成如式（15）所示。

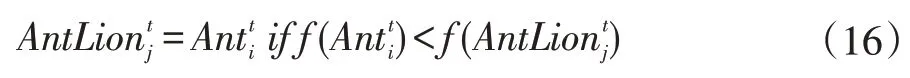
2.2 改进的蚁狮算法

为了使算法能够有更大的可能性找到全局最优点使用混沌反向学习初始化来代替原算法的随机初始化。混沌初始化具有随机性和遍历性，能使能使初始化的个体位置尽可能的遍布于整个解空间，其搜索效率明显好于随机初始化[5]。基于反向学习（Opposition-Based Learning，OBL）最初由Tizhoosh 于2005 年推出，已被证明是一种增强各种优化算法的有效方法。其主要通过计算反向解来提高找到全局最优解的几率，从而提高算法的收敛速度[6]。具体步骤为：

混沌初始化：本文使用Logistic 混沌算子来对N 个蚁狮位置进行初始化，其中Logistic 混沌算子如式（17）所示。

其中xn是位于0 到1 之间的随机数，通过式（17）得到N 个混沌变量，再将得到的混沌变量用于初始化种群位置。

反向学习：若个体位置表示为X=｛x1，x2，x3，…，xn｝，其 中xi∈[ai，bi]，那 么xi的 反 向 位 置 可 以 表 示 为=ai+bi-xi。我们先得到N 个混沌初始化的蚁狮位置，然后在得到N 个与之对应的反向位置，再根据适应度值从这2N 个位置中挑选出较优的N 个位置作为最终的蚁狮初始位置。

为了防止算法陷入局部最优解，本文进行了变异操作以帮助算法跳出局部解。

根据差分算法，我们对蚁狮进行变异得到变异后的蚁狮位置如式（18）所示。

其中xE是精英蚁狮位置，xworst是适应度最差的蚁狮位置。对产生的变异蚁狮若其适应度优于精英蚁狮则代替精英蚁狮，反之若优于最差的蚁狮则代替该蚁狮。

对精英蚁狮XE=｛x1，x2，x3，..，xn｝中随机选择一个元素xi令xi=li+rand*(ui-li)，若变异后的适应度更优则代替原精英蚁狮，反之则保持不变。这样子有助于在算法迭代后期对精英蚁狮周围的探索，跳出局部解。同时为了平衡算法的探索与局部收敛能力，对式（15）改为：

为了对算法改进的有效性进行简单说明，本文选取了几个基本测试函数进行测试，测试函数信息如表1所示，测试结果如图（1-3）所示。

从上面三个函数的收敛过程中可以看出：①在迭代初期，改进的蚁狮算法的最优值比较好，能够有效增加收敛速度，说明了混沌反向初始化的有效性；②改进的蚁狮算法在迭代过程中能有效的跳出局部最优点，而原始的蚁狮算法不能很好地做的该点，很好地体现了对原算法进行变异的作用。

广义预测控制中的柔化因子a 和权重系数λ都是需要人为进行给定的参数，而对于给定的被控对象，通过手动调速这两个参数往往繁琐而且难以达到满意的效果故在本文中将改进的蚁狮算法同广义预测控制相结合[7]，通过算法来优化优化这两个参数以得到满意的效果，而目标函数选取为均方方差（MSE）如式（20）所示：

其中SP 是设定值，y 是控制输出。

3 对T-S模糊模型的控制

T-S 模糊的模糊规则是通过IF-THEN 规则来进行描述的：

其中xi是输入；Air是第i 条规则的第r 个模糊集；pir是后件部分的系数；R（i）表示第i 条模糊规则。而整个T-S 模糊系统的输出是各个模糊规则的加权平均和，具体可以表示为：

其中C 是模糊规则数；wi是第i 条规则所占权重。T-S 模糊辨识建模就是确定模型前件部分和后件部分的结构和参数。注意到模糊规则的THEN 部分同广义预测控制的CARIMA 模型具有相似之处，故本文使用广义预测控制来对T-S 模糊模型进行控制。

智能材料今年来发展非常迅速，已经被广泛应用于精密机床、微纳米平台等，然而智能材料具有的迟滞非线性是对智能材料应用的一大阻碍，它会影响系统的稳定性，和造成精度下降等问题。那么对迟滞非线性的控制研究是必不可少的。

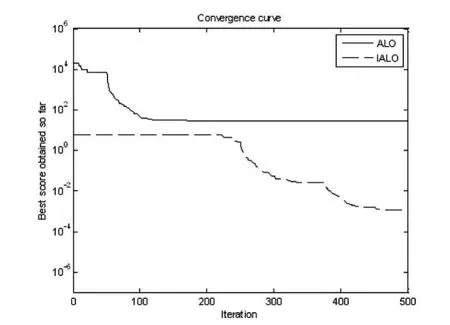
图1 函数f1收敛过程

表1 测试函数信息

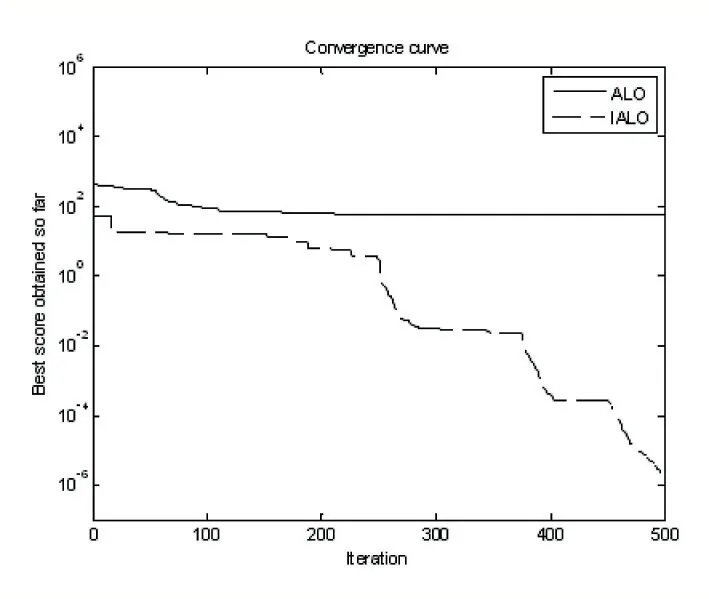
图2 函数f2收敛过程

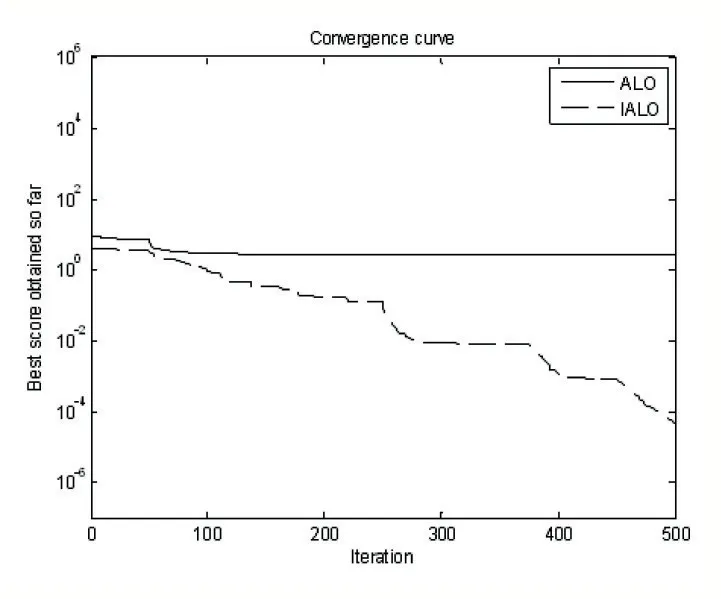
图3 函数f3收敛过程

我们使用T-S 模糊模型对迟滞非线性建模。先用如式（22）所示的电压信号，以10kHz 的采样频率输入Duhel 模型以得到对应的输出（注意到所用的输入电压信号的幅值不断减小，周期不断增大），得到的动态模型训练效果如图（4）所示。

图4 T-S建模结果

对该模型用基于改进蚁狮算法的广义预测控制进行控制并将控制结果同单用广义预测控制的结果相对比如图5、图6 所示。

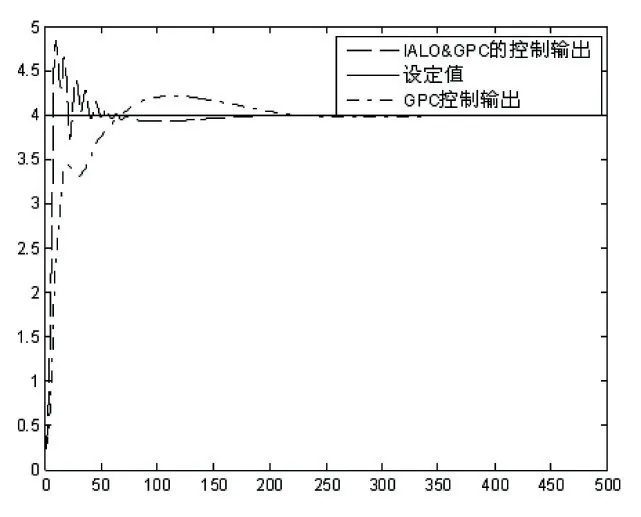
图5 控制结果对比

图6 控制追踪结果对比

图5 是将系统控制到设定值4，从图中可以看出使用改进蚁狮算法同广义预测控制相结合能够更早地达到设定值；图6 是将系统的输出跟踪曲线4e-13tsin（2π×62t×e-t）+1 的结果，从图中可以明显看出所提出方法能够更好地追踪目标曲线。

与此同时，对系统的模型加入了扰动来测试其抗干扰能力，结果如图7 所示。给模型加入扰动，系统也能够很好地恢复到稳定。

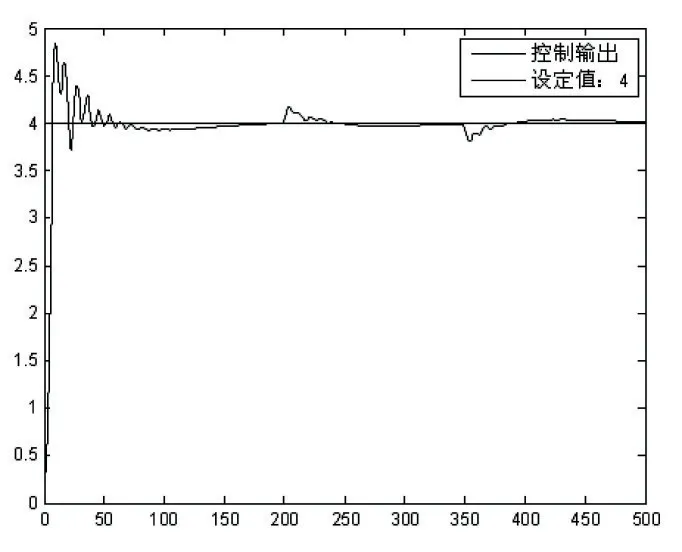
图7 加扰动后控制结果

4 结语

本文对已有的蚁狮算法进行了改进，并将其同广义预测控制相结合，通过优化广义预测控制的参数，来达到更好的控制效果，并将其用于对T-S 模糊模型的控制，进行仿真分析，证明了所提出方法的有效性。