米兰科维奇旋回识别的信号分析方法研究
2020-03-04刘浩童
刘浩童
(长江大学地球科学学院,湖北武汉 430100)
米兰科维奇理论最早是由南斯拉夫学者米兰科维奇米留廷提出,随着地质学研究的不断深入,科研人员发现米兰科维奇旋回可以反映地层中的地质时间信息。在地层学的研究中,米兰科维奇理论应用的时间比较长,并且越来越受到研究人员的重视,该理论主要可以应用在2个方面:地层的划分对比和地质定年[1-3]。但是,如何从资料缺乏的地层记录中,对米兰科维奇旋回进行有效地识别是目前地质学界的热点和难点。
一般情况下,研究人员都会利用露头、岩心、地震数据等资料对沉积旋回进行识别分析和研究,但是这些方法存在一定的缺陷,很难识别分辨率较高的沉积旋回。据有关研究发现,复杂的周期事件都是由很多个具有不同周期的简单事件相互叠加组成的,而不同的沉积旋回是地质沉积事件的周期性重复的简单事件,由于测井曲线可以反映一定时间内各种沉积事件,因此,可以用测井曲线来描述各种沉积特征,如地层的旋回性、周期性等。虽然不同类型的测井曲线反映的地层物理特征不同,但是它们所反映的地层沉积旋回是相同的,因此,可以利用测井曲线来识别和分析米兰科维奇旋回[1-3]。
1 频谱分析法
通常使用时间序列中的频率来描述某一事件周期性发生的频繁程度,而频谱分析是一种十分常用的研究周期性事件的数学方法。为了便于从某一时间序列中获得频率,并且让这个频率可以更加直观的呈现出来,一般而言都是采用傅里叶变换将信号从时间域转化到频率域。根据傅里叶变换的相关理论,任何信号都是由正弦波或余弦波组成,而且这些正弦波或余弦波的波长和振幅都具有一定的规律。据有关研究表明,大部分地层中的时间序列可以近似为各种正弦波构成的一种信号。同理可知,得到的各种测井曲线是由不同的信号组成,存在各种规律的旋回,而且每一种旋回都有它特有的频率,频谱分析法就是利用傅里叶变换来获得这些特有频率[1-2]。因此,可以使用频谱分析法处理各种测井曲线,在频谱分析的结果中,获得的频率值越大,表明沉积周期越短,地层的旋回厚度越小。而曲线图中的功率高点表示该频率的沉积旋回在地层中的控制作用就越强,在地层中出现的次数越多,因此该频率就对应于曲线的主要频率,因此,求出频谱分析结果中的主要频率值,就可以计算出对应的波长,从而可以获得旋回周期。图1是某地区的B井的自然伽马曲线和电阻率曲线的频谱分析结果,从图1可以看出,其主频周期和主频周期之比具有较好的一致性,并且可以证实该地区保存了米兰科维奇旋回[4]。

图1 某地区A井曲线频谱分析图
2 小波分析法
小波分析法是一种通过改变时间-频率窗口的形状,对信号中的低频成分,采用宽窗口,对信号中的高频成分,采用窄窗口,从而在时间域和频率域都可以获得较好的信号局部信息的信号分析方法。因此,利用小波分析法可以将测井曲线分解成不同的频带的信号,这些信号代表不同周期的沉积旋回,然后再将信号在一定尺度上进行分解,进而可以获得相应频带的信息,从而得到相应的沉积周期[3-4]。小波变换的尺度值越大,说明该沉积周期的时间越长,对应的沉积旋回厚度越大。根据相关研究表明,通过小波分析法对测井曲线进行处理,可以获得的小波能量谱图以及不同尺度的曲线,然后对这些能量谱图和曲线的特征进行分析和研究,就可以获得地层的旋回性和各级层序之间的对应关系,而其中的高频层序和米兰科维奇具有一定的对应关系。图2是某地区B井的自然伽马曲线小波分析结果,首先利用分析的自然伽马低频部分划分了6个三级旋回,然后利用小波分析的能量图和谱图划分了25个四级旋回。
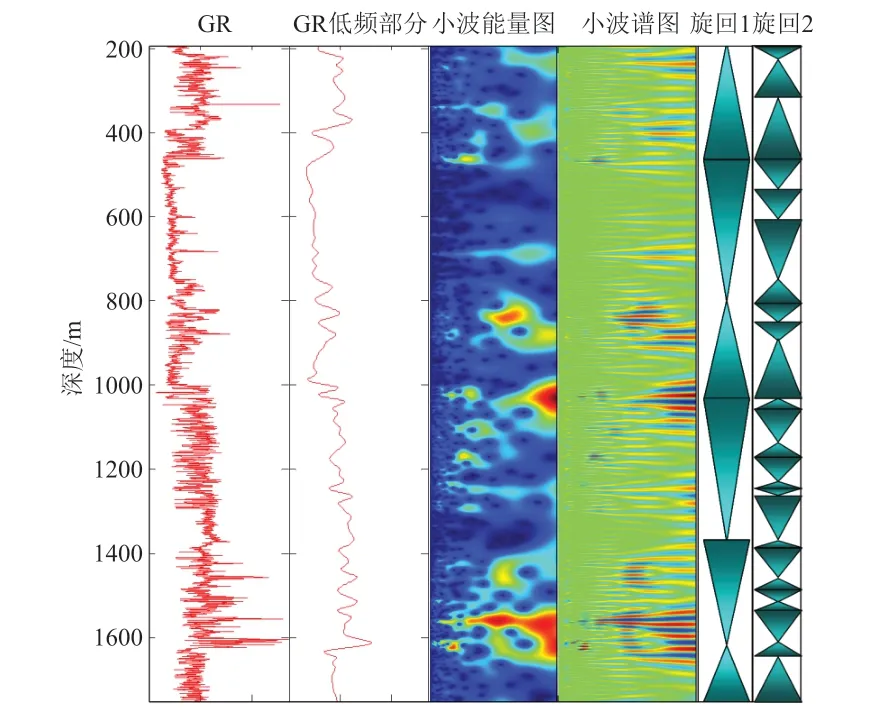
图2 B井旋回分析图
3 结论
1)频谱分析法的优点是可以给出一系列频率点上的信息,细腻地反映测井曲线中的高低频率特征,进而可以提取其中所包含的地质信息,而且计算速度非常快,使用起来十分方便。但是,频谱分析法计算结果的不确定性太强,精度太差。
2)小波分析方法可以从测井曲线中提取其相应的时频特征,特别是这种方法可以在不同尺度下,以不同分辨率对测井曲线中隐藏的沉积周期成分进行分析,在一定程度上减少了人为因素的影响,提高了米兰科维奇旋回识别的准确度。
