基于动态模糊Petri的电力通信现场故障诊断方法研究*

施 健于 蒙 赵 阳 赵子兰

（1.南瑞集团有限公司（国网电力科学研究院有限公司） 南京 210003）（2.国网冀北电力有限公司 北京 100053）

1 引言

近年来，电力通信网络的规模得到快速增长，有效提高了电网生产运行、企业经营管理的安全水平，保障了电力系统在恶劣环境与意外灾害下各类信息传输的可靠性与稳定性。通信网架拓扑的日益复杂，使得各通信子系统之间的耦合程度越来越紧密，给现场运维与故障排除带来了不利影响。随着信息通信技术的高速发展，各类专业网管系统、智能电气装置、监控传感器等设备在电力通信网络不断得到推广与应用，为现场的故障诊断提供了所需的多信源数据。如果对这些能够表征通信网络运行状态的多信源数据进行有效利用与识别，可以为通信现场的故障诊断提供技术支撑。针对通信网络中存在的由于单点故障造成的系统性风险，需要能够快速及时地发现可能存在的潜在隐患，准确诊断并消除故障风险，从而提升电力通信系统的安全可靠性［1～2］。因此，迫切需要研究并构建一套科学高效的通信现场故障诊断方法。

在电力通信网络中，通信设备与通信光缆之间呈现的是一种网状拓扑关联关系，Petri网模型作为一种图形和数学融合的建模方法，可对多种活动过程进行定性和定量分析，这与通信网络故障发生和处理过程相类似［3～5］。随着 Petri网模型研究的深入，又进一步提出了模糊Petri网（Fuzzy Petd Net，FPN）的概念，利用模糊集合理论对不确定的或主观的参量进行分析，使其更符合一般人类正常的思维习惯和认知方式，以直观的表达方式和矩阵运算方法解决网络诊断的难题。

本文基于模糊Petri网理论，提出了一种动态电力通信网现场故障诊断方法，有效避免了模糊Petri网在故障诊断过程中由于人为主观因素造成的误差，提高了推理过程的准确性。仿真结果表明该方法具有较好的适应性和通用性，为通信现场故障诊断提供了新思路。

2 模糊Petri网基本原理

FPN基于模糊集合理论与传统Petri网，其能准确而清晰地描述与分析模拟系统中各组成要素不确定的模糊状态信息，主要的改进之处在于FPN中对每个库赋予一个[ ]0，1之间的实数作为其置信度值，并给每个转移定义一个确定因子（Certain Factor，CF）表示其发生的可能性概率。而规则推理过程用推理Petri网中转移的触发表示［6～10］。

一个典型的模糊Petri网通常为是一个七元组：

3 基于模糊Petri网的改进算法

电力通信现场发生的故障根原因复杂多样，相互之间存在着众多的关联关系，利用传统的模糊Petri网模型构建会变得复杂庞大，直接导致故障信息与传播路径表达不够明确、清晰。针对电力通信现场呈现的多层次、非线性、多变量及多关联等故障特征，本文在模糊Petri网理论的基础上，引入位置（Place）、令牌（Token）及转移的着色规则，提出了一种适用于通信现场故障诊断的改进动态模糊Petri网算法［11～15］。

动态模糊Petri网（Dynamic Fuzzy Petri Net，DFPN）算法定义为一个12元组

其中

3）I：U×V为输入矩阵，表示从位置故障结点ui到转移规则结点vj的一条有向弧，它是转移规则结点vj的输入弧，而ui是转移规则结点vj的输入位置故障结点。式中，i=1，2，…，n，j=1，2，…，m。

4）O：U×V为输入矩阵，表示从转移规则结点vj到位置故障结点ui的一条有向弧，它是转移规则结点vj的输出弧，而ui是转移结点vj的输出位置故障结点。式中，i=1，2，…，n，j=1，2，…，m。

9）P=为位置事件模树故障的概率集合，pi表示位置故障结点ui代表故障事件发生的概率大小。

10）α=(为故障事件的置信度向量，αi表示位置故障结点ui真实程度的置信度，具有一定的模糊性，αi∈[0 ， 1]，i=1，2，…，n。其初始值由α0表示，并根据历史运行数据、专家知识经验等设定初始值。

11）λ=为转移规则阈值集合，λj表示转移规则结点vj点火的阈值2，…，m。

设 定 ∀v∈V，若则称转移规则结点v是使能的(j=1，2，…，n)。

4 算法的仿真实现与分析

4.1 动态模糊Petri网建模规则

动态模糊Petri网的建模流程主要包括分析电力通信网络的拓扑结构，依据故障事件的模糊规则判定故障事件存在的逻辑关联关系。同时为清晰、准确表达故障模糊信息，以及通信现场的故障传播特性，通过位置着色规则的定义和设定令牌着色规则的故障置信度等级，最终完成动态模糊Petri网的建模。如图1所示。

1）位置着色规则

若U×V→N=1，V×U→N=0，则设定该位置为初始位置，即为现场故障的根原因，用“◎”表示该位置U的状态。若含有令牌着色，则表示发现现场故障的根原因。

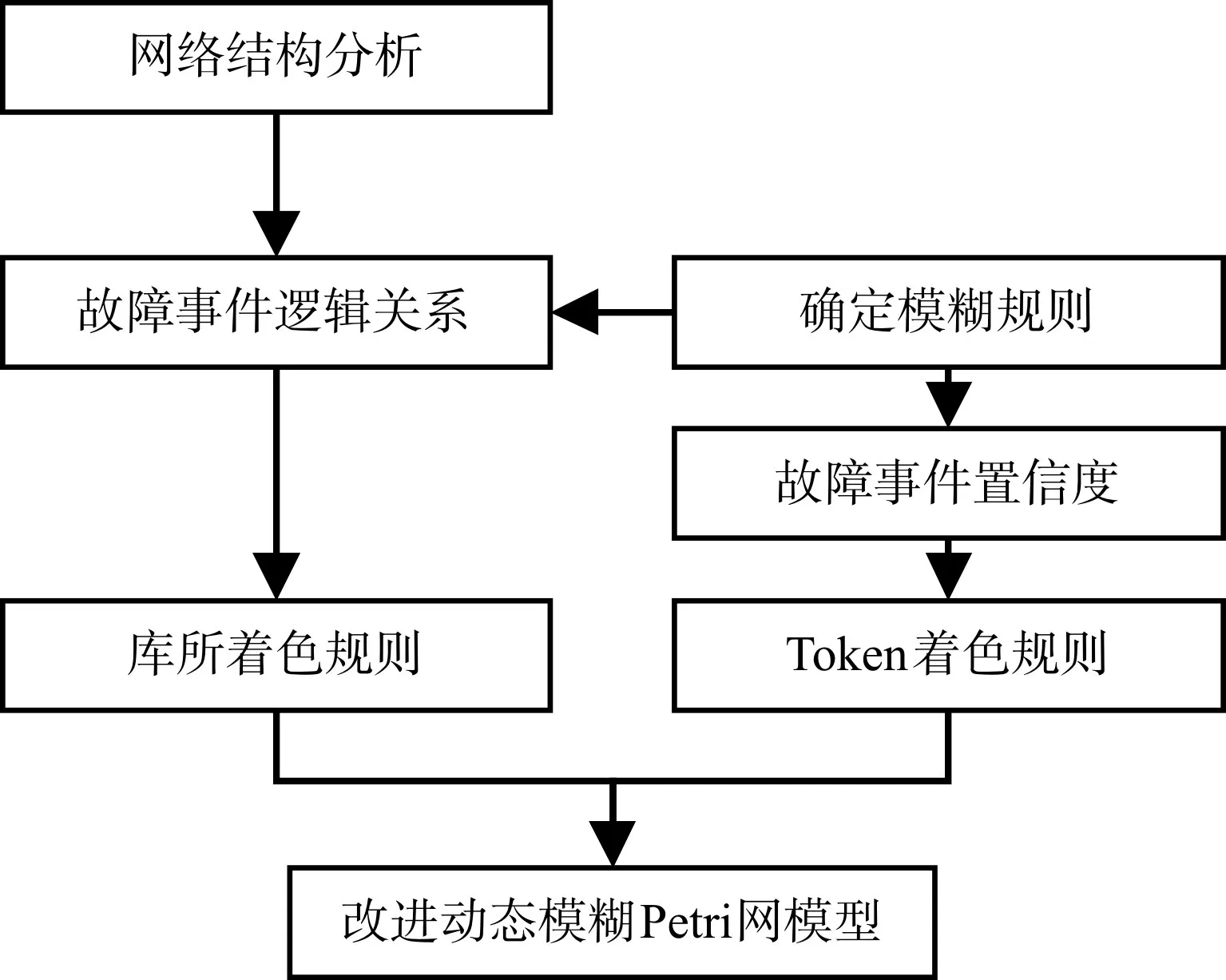
图1 动态模糊Petri网的建模流程图

若U×V→N=1，V×U→N=1，则设定该位置为中间位置，即现场为故障模式，用“〇”表示。

若U×V→N=0，V×U→N=1，则设定该位置为最终位置，即为系统故障，用“◎”表示。

如图2示例所示，u1，u2，u3为初始位置，u4为中间位置，u5为最终位置。

图2 Place着色规则示例图

2）令牌着色规则

通过对电力通信现场的故障诊断研究，设定故障置信度范围为(0 ～1)。为了更加直观、可视地表示故障信息，本文引入了令牌着色规则以反映现场故障事件的置信度等级。

表1 令牌着色规则

4.2 动态模糊Petri网故障诊断方法

动态模糊Petri故障诊断方法主要有以下几步骤，具体如图3所示。

1）根据历史运行数据、专家经验知识和实际监测采集数据等，确定各输入位置的权值、转移的置信度和阈值、以及初始位置的置信度和故障概率等模型初值，通过置信度矩阵计算，从而推理出各位置故障事件的置信度，并为故障的智能推理提供必要条件。

2）基于各位置的置信度和模糊转移规则，计算得到潜在使能的转移序列，从而为后续的智能推理点火判断提供依据。

3）当系统无故障发生时，通过在线监测设备预测通信网络中可能存在的故障征兆，确定初始标识，利用点火转移序列判断对故障状态进行正向智能推理，进行评价当前网络故障的状态情况。

4）当系统发生故障时，确认已发生故障的现象，反向智能推理出位置逆向可达序列，根据故障关联矩阵追溯最可能发生的故障源，从而为通信设备的抢修提供指导依据。

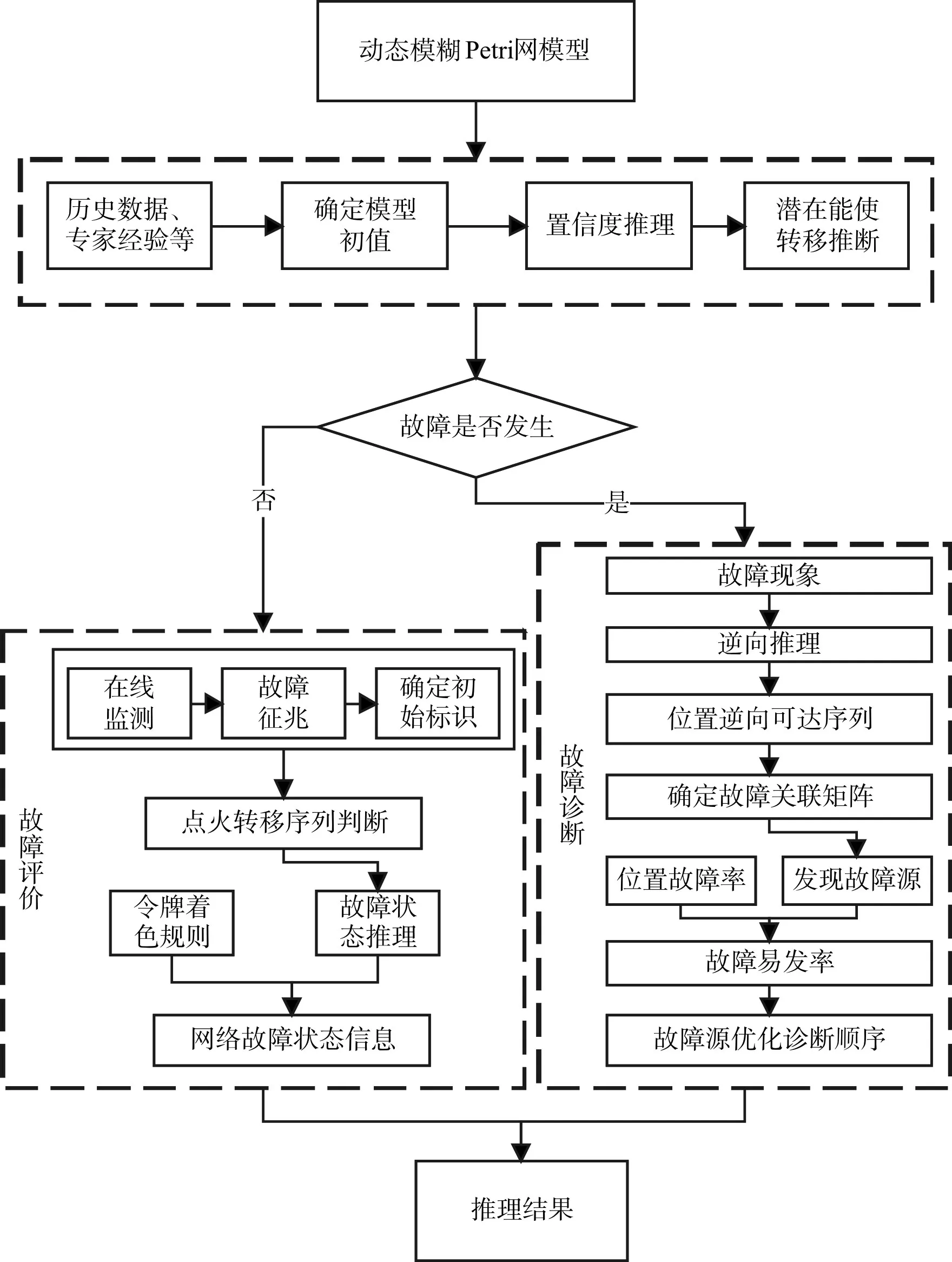
图3 动态模糊Petri网的故障诊断推理图

4.3 实验验证

本文以电力通信现场的传输设备故障为例，利用专家经验知识将模糊规则库的模糊规则映射到对应的动态模糊Petri网故障模型，其初始状态如图4所示。

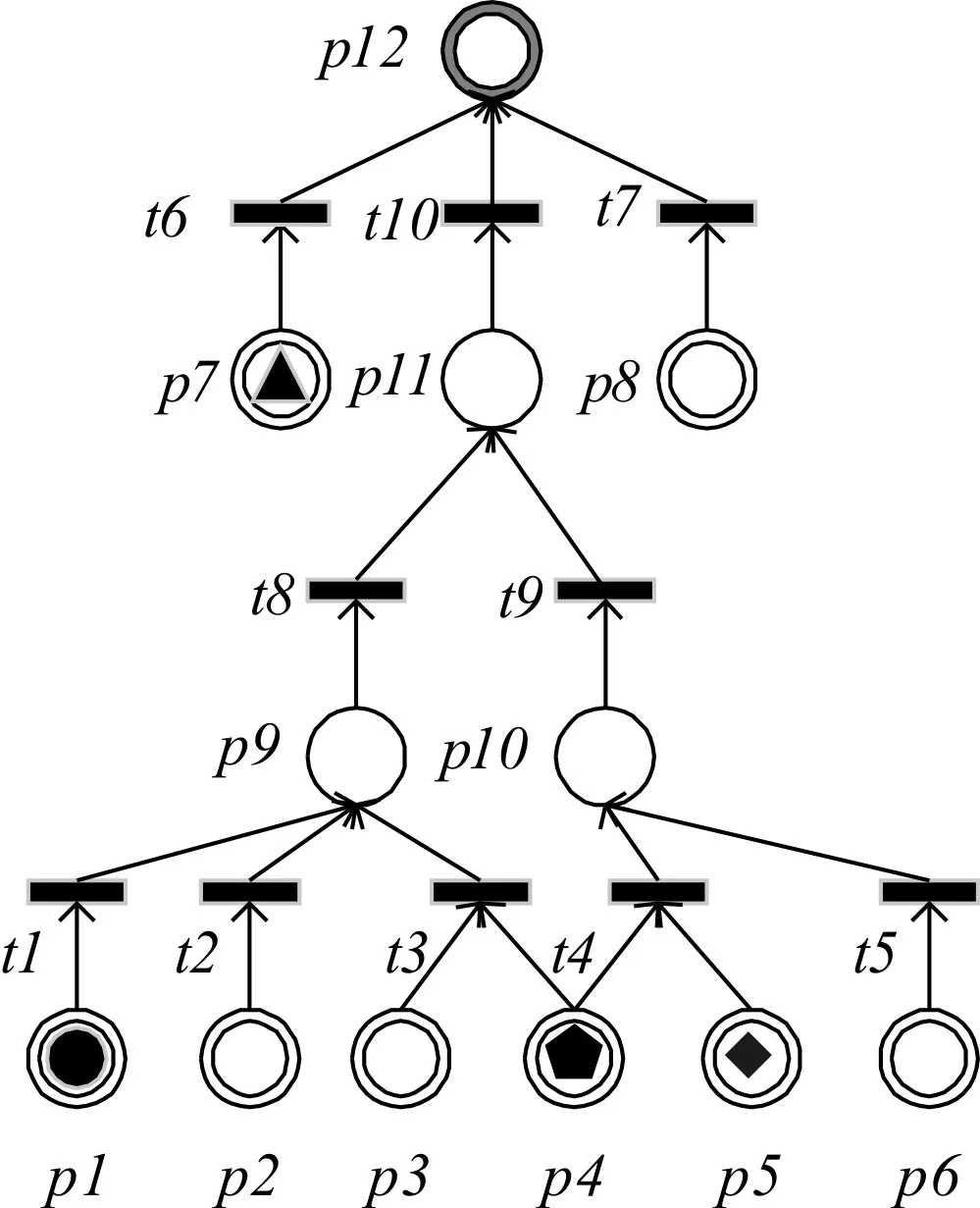
图4 动态模糊Petri网故障模型图

从电力通信现场历史运行数据中提取出与传输设备相关的故障记录共计792条，其中，关于“p11光功率不稳定”的故障诊断推理数据及实际故障记录数据共计724条，如表2所示。

表2 数据统计结果

在表2中，对采用动态模糊Petri网模型得到的推理结果和实际历史发生的故障统计次数进行归一化处理，得到的对比关系如图5所示。

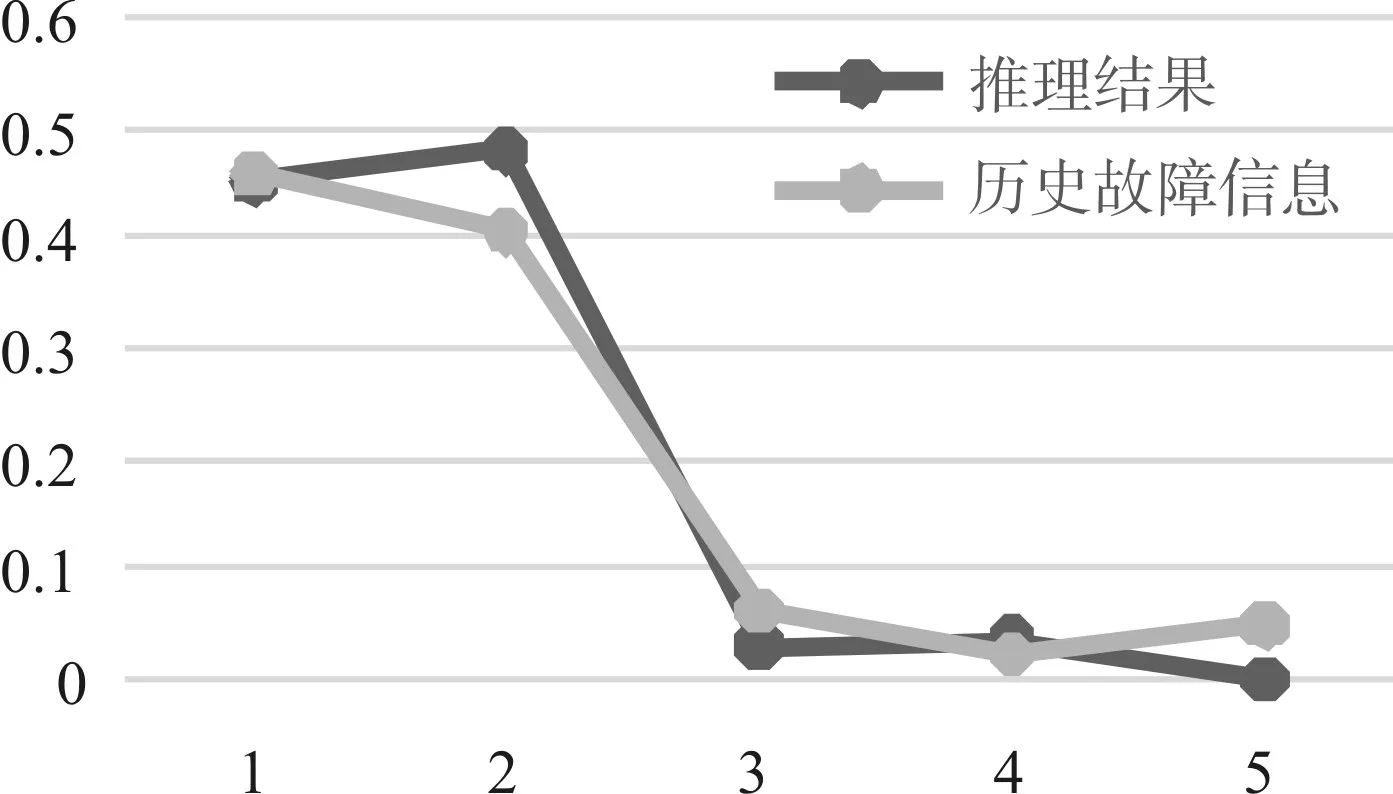
图5 推理结果及历史故障统计归一化对比图

通过上述仿真实验验证可知，本文利用动态模糊Petri网模型对电力通信现场故障进行故障推理诊断，其推理结果与现场实际的历史故障具有较强的线性相关性，具有较好的实用价值。

5 结语

针对电力通信现场故障特征呈现出多层次、非线性、多变量及多关联等特点而引起的现场故障诊断难以实现的问题。本文对电力通信现场的故障状态评价及诊断问题进行了深入研究，以模糊理论和Petri网理论为核心，通过引入Place、令牌及转移的着色规则，提出了一种动态模糊故障Petri网的故障模型及建模规则，应用于电力通信现场的故障推理。

利用算法仿真对改进后的模糊Petri网模型算法进行试验验证，通过推理结果与历史故障统计的归一化数据对比，验证了本故障诊断方法的正确性、有效性及可行性，具有较好的可行性和实用性，可为电力通信现场的故障诊断提供辅助分析支持。但同时，在2和5处的故障原因诊断存在有一定的偏差，因此，后续有必要对产生这种偏差的原因进行进一步研究分析，改进模糊Petri网模型算法，使得电力通信现场的故障诊断能够达到更加理想的效果。