基于Word2Vec的改进密度峰值新闻话题聚类*
2020-03-04胡建洪
高 鑫 徐 建 胡建洪
(南京理工大学计算机科学与工程学院 南京 210094)
1 引言
根据2017年8月份中国互联网络信息中心(CNNIC)发布的《第40次中国互联网络发展状况统计报告》[1]中的数据,截至2017年6月,我国网络新闻用户规模为6.25亿,半年增长率为1.7%,网民使用比例为83.1%。随着网络新闻的急剧增长,新闻信息逐渐变得庞大臃肿。这给人们从海量数据中获取自己感兴趣的信息带来了极大的困难。新闻话题聚类在信息检索、热点话题发现、舆情监督等多个领域都有着广泛的应用,有助于人们掌握社会最新动态,及时把握社会舆论走向。
近年来,国内外学者对新闻话题聚类做了大量的研究,并取得了卓有成效的结果。新闻话题聚类的研究主要集中于话题模型表示与聚类算法改进。Spitters[2]首先基于语言模型表示新闻文本以及计算文本之间的相似度,但存在数据稀疏的问题。James Allan[4]最早采用向量空间模型来表示新闻文本,根据余弦相似度来计算新闻的相似度,但忽视了新闻报道之间语义的关系。李凤岭[6]等在基于微博的话题发现领域引入了LDA模型,增加了对文本语义相关方面的研究。但LDA模型话题数目需要预先指定且一直不变,并不能有效地抽取正确的话题。Bengio[7]等将分布式表示应用于单词,结合神经网络,训练语言模型,成功解决了传统概率语言模型中的参数组合爆炸以及稀疏问题。在前人研究的基础上,Mikolov[8]等在 2013 年提出了Word2Vec模型来计算词向量。目前,将词向量应用于自然语言处理非常成功,已经被广泛应用于中文分词、情感分类、句法依存分析等。本文基于Word2Vec模型计算词向量并利用词向量来表示新闻文本的向量,然后通过改进密度峰值聚类算法来进行新闻话题聚类以提高聚类精度。
2 相关工作
2.1 词语的分布式表示
Hinto[10]在 1986年提出概念的分布式表达开创了词语的分布式表达的先河。与独热表示只使用向量的一个维度不同,分布式表示用稠密实数向量来表示一个词语,能充分表达词语之间的语义关联,有效缓解数据稀疏问题。分布式表示自提出以来,已被广泛应用于单词、短语、概念、句子、文档和社会网络等对象的表示学习中。其中,最经典的是由Bengio提出的用一种三层的神经网络来构建语言模型,在此基础上研究者们又进行了一系列的研究分析,其中较为出众的要属Word2Vec。Word2Vec的核心是神经网络的方法,采用CBOW和Skip-Gram两种模型,将词语映像到同一坐标系,得出数值向量。CBOW的目标是根据上下文来预测当前词语的概率。Skip-gram和CBOW刚好相反,其根据当前词语来预测上下文的概率。起初每个单词都是一个随机N维向量,之后利用CBOW或者Skip-gram模型就可以获得每个单词的最优向量。
2.2 新闻话题聚类
新闻话题聚类是话题检测与跟踪的一项内容,它利用文本聚类技术对大量的新闻文本聚类以发现相关话题。在以往的研究过程中,许多学者在新闻话题聚类方面做出了重大的贡献。索红光[11]等通过优化局部搜索能力来改进K-means算法,提高了文本聚类的精度。但随机选择初始聚类中心使得该算法对初始聚类中心选择敏感,结果波动性较大。HuangB[12]采用了LDA模型对微博中的短文本数据建立数学模型,并且采用单遍聚类算法对话题进行聚类检测。这种结合单遍聚类的聚类方法虽然方便,但是结果很容易受到文本输入顺序的影响。McCallum A[13]等提出两层聚类方法,解决高维度大数据量问题。但划分容易先形成规模大的Canopy,影响后面话题精确聚类的效率,而且初始种子选择不当会导致迭代次数和冗余度增加。Rodriguez A[14]等提出了一种快速搜索发现密度峰值的方法,可以方便快捷地确定类簇。但是在选取类簇中心时需要通过人工来选择,存在一定的主观性。经过研究发现,基于密度的聚类算法能够识别任何形状的类簇,而且不需要提前给出聚类数目,还能比较好的识别出异常点,因此获得了广泛的使用。本文将通过改进密度峰值聚类算法来对新闻文本进行聚类,以达到发现新闻话题的目标。
3 基于Word2Vec的话题聚类算法
3.1 新闻的分布式表示
一篇新闻由很多的词语组成,如何利用词向量有效地表示新闻文本是话题聚类的关键。当前常用的方法有对所有的词求平均值[15]、对所有词进行TF-IDF加权求平均值[16]以及Doc2Vec模型[17]。本文提出一种基于Word2Vec选取核心词(core words)来表示新闻文本的方法,也称作CW-Word2Vec。
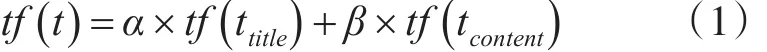
其中α为标题的权重,β为正文的权重,tf(ttitle) 表示词t在标题中的词频,tf(tcontent)表示词t在正文中的词频。
对每篇文章中的分词利用词向量计算这篇文章中距离此分词最近的k个词,以余弦距离作为两个分词间的“距离”。以词t为例,将距离词t最近的k个词的距离分别乘以词频然后累加再乘以词t的词频得到词t的权重值。词t的权重值计算公式如下:
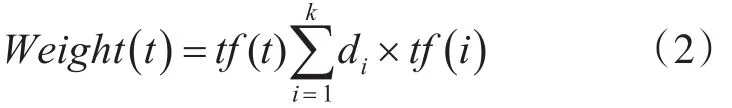
其中di表示第个词与词t的距离,tf(i)表示第i个词的词频。
计算出文章中每个词的权重值以后,根据权重值进行排序,取前n个词表示文章的核心词,用这些核心词的向量均值表示文章的向量。文章i的向量计算公式如下:

其中,wt表示核心词的词向量。
3.2 改进密度峰值聚类算法
密度峰值聚类算法(clustering by fast search and find of density peaks,DPC)由 Rodriguez等在2014年提出,该算法通过快速搜索发现密度峰值,然后选取密度峰值较大的样本作为聚类中心,然后将剩余样本指派到合适的聚类中心完成对数据集的聚类。DPC聚类算法通过引入样本i的局部密度ρi和样本i到局部距离比它大且距离它最近的样本j的距离δi来确定聚类中心,局部密度 ρi和距离δi的定义分别如式(4)和式(5)所示:

其中,dij为对象i,j间的距离,dc为截断距离,当x<0时,χ(x)=1,否则 χ(x)=0。

对于局部密度 ρi最大的样本i,其当数据集较小时,可以通过高斯核函数来可靠地估计对象的局部密度,如式(6)所示。
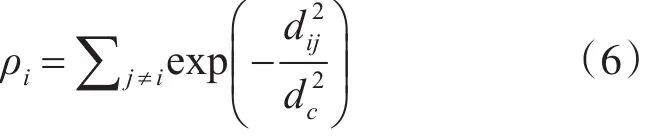
当通过式(4)和式(5)计算出所有样本点的局部密度 ρi和距离 δi后,可以构造点( ρi,δi)在二维平面上的决策图,然后通过可视化方式选取图中ρi和δi都相对较大的点作为聚类中心。然而在有些情况下,由于数据的稀疏性导致聚类划分的类簇个数不是很容易确定,很难确定聚类中心个数,因此Rodriguez等人给出了一种通过计算ρ和δ的乘积来选择聚类中心数量的方法,如式(7)所示:

通过式(7)计算出所有样本的γ值后,将每个样本点的γ值按降序排序,γ值越大越有可能是聚类中心。通过判断γ的第一次跳跃点可以找到各类簇的中心点,选取γ最大的k个样本点为聚类中心。
DPC的主要优点是计算过程简单,无需迭代,易于理解,但存在的问题也比较明显,主要存在的问题有截断距离dc设置困难、聚类中心选取困难、存在多米诺骨牌效应、同一类簇多密度峰值问题等4个问题[18~20]。
局部密度作用是发现密度峰值较大的样本,因此局部密度的计算方法应该使得密度峰值大的样本突出,同时平滑密度峰值小的样本,因此本文使用高斯核函数来计算每个样本点的局部密度。为避免截断距离dc取值困难问题,本文使用样本点的K最近邻来自适应计算截断距离dc,计算方法如式(8)所示。


通过式(10)和式(5)计算出的样本点 ρ值和δ值可能处于不同的数量级,因此本文通过离差标准化将 ρ和δ归一化到[0,1]区间,归一化后的决策值的计算如式(11)所示。
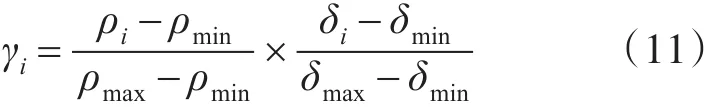
其中,ρmax表示样本局部密度的最大值,ρmin表示样本局部密度的最小值,δmax表示样本到高密度点距离中距离的最大值,δmin表示距离的最小值。
DPC算法在绘制决策图后,通过肉眼观察决策图确定和选取聚类中心,然后对剩余样本进行指派完成聚类。然而通过肉眼观察跳跃现象具有主观性,不同的人可能选择的聚类中心不同,不利于算法的自动化。因此本文通过最小二乘法拟合直线的方法在决策图中自动确定最佳聚类中心集合。
假 设 决 策 图 中 有 点 集 DP={(xi,fi),(xi+1,fi+1),…,(xn,fn)} ,点 集 DP 的 最 佳 拟 合 直 线 为f=a0+a1x,则通过最小二乘法计算直线 f的误差平方和S的方法,如式(12)所示:

为了得到S的最小值,可以对S求偏导数,令这两

等价变换为

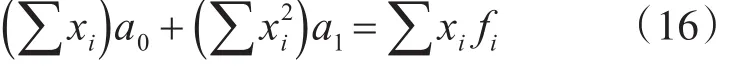
通过求解方程组即可得到参数a0和a1的值,分别如式(17)和如式(18)所示:

将式(17)和式(18)求出的 a0和 a1,代入式(12)即可求出拟合直线的误差平方和S。
设决策图中所有点的集合为D={(x1,f1) ,,现在把集合 D分为左点集 Dl和右点集 Dr两个部分,其中 Dl和 Dr分别如式(19)和式(20)所示,Dl为聚类中心的集合。

因此,为求出最佳聚类中心集合,首先分别求出集合Dl和Dr的拟合直线的误差平方和Sl和Sr,然后通过式(21)求出总的均方根误差平方和RMSEP。

通过改变划分点 p的值,求最小的均方根误差平方和RMSEmin对应的左点集Dl,即为最佳聚类中心集合。
当数据集较大时,选择初始聚类中心将非常耗时,需要做相应的优化。考虑到聚类中心为γ值最大k个点,通常聚类个数k也不会很大,因此可以选择γ值最高的m个点参与选择初始聚类中心即可,本文根据实验经验通过式(22)确定m的值。

因此,本文通过最小二乘法线性拟合选择最佳聚类中心集合的具体过程如算法1所示。
算法1初始聚类中心选择算法
输入:降序排序后的γ值集合D及其大小m
输出:初始聚类中心集合C
算法步骤:
1.初始化聚类中心集合C为空;
2.初始化最小均方根误差平方和RMSEmin为无穷大;
3.forp←2 to m-1
4. 根据划分点 p将集合D划分为左点集Dl和右点集Dr两部分;
5. 使用式(12)分别求出集合Dl和Dr的拟合直线的误差平方和Sl和Sr;
6.使用式(21)根据Sl和Sr求出总的均方根误差平方和RMSEP;
7.ifRMSEP<RMSEmin
8. RMSEmin=RMSEP;
9. C=Dl;
10.end if
11.end for
12.返回初始聚类中心集合C
为了避免离群点对样本归类结果的影响,导致将两个类簇合并为一个类簇的现象出现,在将样本归类到相应类簇前,先进行离群点剔除。本文通过样本i与其K近邻的最大距离和阈值dt来识别离群点,当样本i的大于阈值dt时,则样本i为离群点。和dt的计算方法分别如式(23)和式(24)所示。
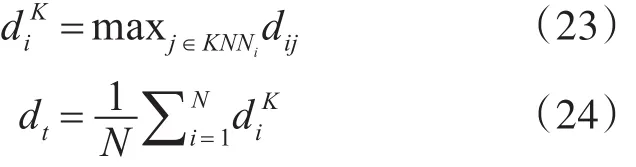
其中,N为数据集样本总数,KNNi是样本i的K个近邻集合。
本文首先对非离群点样本进行分配,然后分配离群点样本,具体算法过程如算法2所示:
算法2剩余样本分配到聚类中心的过程
输入:聚类中心集合CI
非离群点样本集合S
离群点样本集合O
输出:初始聚类结果C
算法步骤:
1.初始化队列Vq为空;
2.for each样本i inCI
3. 将样本i作为一个新类簇的聚类中心,标记样本i已访问,同时将样本i的K近邻集合KNN(i)中每个样本并入样本i所在的类簇,并将KNN(i)的每个样本加入队列Vq;
4. whileVq不为空
5. 取出队列Vq的样本j,对于集合KNN(j)中每一个样本r,若样本r没有被访问,且不是离群点,则将样本r并入样本j所在类簇,标记样本r已访问,并将样本r放入队列Vq;
6. end while
7.end for
8.for each样本i in离群点样本集合O
9. 计算样本i的K近邻归属最多的类簇Cu,将样本i并入类簇Cu
10.end for
11.return初始聚类结果C
本文针对密度峰值算法存在的问题,提出了一种基于KNN改进的密度峰值聚类算法。该算法首先使用样本的K近邻集合自适应计算出截断距离dc,然后计算出每个样本的 ρi和δi,并作归一化处理,计算每个样本的γ值并降序排列;然后通过最小二乘法线性拟合选取初始聚类中心,并使用算法2将剩余样本归类到合适的聚类中心形成聚类结果。具体过程如算法3所示:
算法3基于KNN改进的密度峰值聚类算法
输入:数据集D
对象的K近邻K
输出:聚类结果C
算法步骤:
1.预处理数据集,如归一化或降维处理;
2.根据距离度量公式计算样本间的距离,并通过式(8)计算截断距离dc;
3.分别使用式(10)和式(5)计算每个样本的 ρi和 δi,计算每个样本的γ值并降序排列;
4.使用算法1选取初始聚类中心;
5.使用算法2将除聚类中心外的剩余样本分配到合适的聚类中心,生成聚类结果;
6.返回聚类结果C
4 实验及结果分析
4.1 实验评价指标
本文使用纯度、F1值、调整兰德系数(ARI)作为实验评价指标,相关定义如下。
1)纯度。纯度是对某个聚类结果Ci,其中数量最多的类在聚类结果中比例。单个类簇的纯度的定义如式(25)所示:

其中,Ci表示一个聚类结果,ni表示Ci的元素总数,nij表示Ci中,元素属于j类的个数。总体的聚类纯度可以通过单个聚类纯度的加权平均得到,计算方法如式(26)所示。
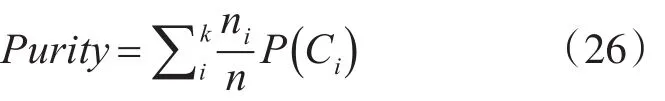
2)F1值。F1值是准确率P和召回率R的调和均值。对于给定的聚类i和类别j,F1值的计算方法如式(27)所示。
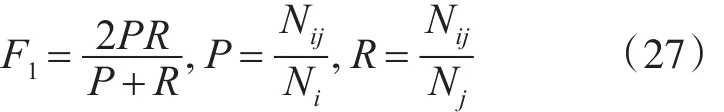
其中,Nij表示在聚类i中类别j的元素个数,Ni表示聚类i的元素个数,Nj表示类别j的元素个数。整体的F1值可以通过类间F1值的加权平均求得,计算方法如式(28)所示。
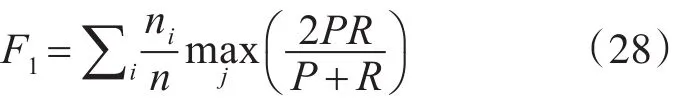
3)调整兰德系数ARI。调整兰德系数根据样本的真实标签和聚类算法得到的标签,计算这两种标签分布的相似性。设和分别表示数据集的真实划分和聚类结果。则ARI的定义如式(29)所示。
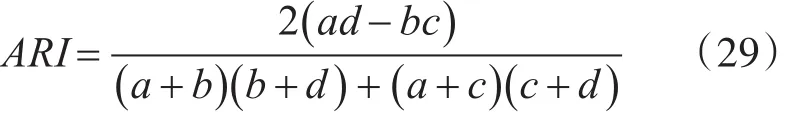
其中,a表示在U和V均在同一类簇的样本对数目,b表示在U中在同一类簇,但在V中不在同一类簇的样本对数目,c表示在U中不在同一类簇,但在V中同一类簇的样本对数目,d表示在U中和V中均不在同一类簇的样本对数目。
4.2 实验环境和数据集
本文的实验环境为Windows 7,64位操作系统,内存 8GB,硬盘 500GB,CPU 为 Inter(R)Core(TM)2 Duo CPU E7500@2.93GHz,Java版本1.7。
本文选择搜狗实验室中2012年6月到7月的搜狐新闻数据集作为实验数据集,并进行聚类实验和实验结果分析。对于搜狐新闻数据集,本文随机选取其中IT、财经、房产、教育、军事、汽车、文化、体育等8个类别下各1000篇新闻文本构成总量为8000篇新闻数据集,然后使用开源中文切词软件Ansj对新闻文本进行切词,并去除常规停用词。
4.3 实验结果及分析
为验证不同文本表示模型对聚类结果的影响,本文分别使用基于TF-IDF的向量空间模型、LDA主题模型以及本文的CW-Word2Vec模型对新闻文本进行特征提取。对于CW-Word2Vec模型,本文采用CBOW模型,模型设置的训练参数为,词向量维度为100,初始学习率为0.025,文本窗口大小为5,标题权重α为0.6,正文权重 β为0.4,n取8。本文使用KMeans++和DPC作为文本聚类的基准方法,来验证本文改进的KNN-DPC聚类算法的可行性和有效性,实验结果如表1、图1、图2以及图3所示。
由实验数据可知,不同的文本表示方法对聚类结果的影响比较大,整体上来说基于CW-Word2Vec模型的聚类结果最好,基于主题模型LDA的聚类结果次之,基于TF-IDF向量空间模型的聚类结果最差。在TF-IDF空间模型和CW-Word2Vec模型上,DPC算法实验结果比KMeans++和KNN-DPC的实验结果要差。在LDA主题模型上,三种聚类算法的实验结果差距较小。通过对比在三种文本表示模型上聚类的各项指标,可以发现KNN-DPC的实验结果整体上要优于KMeans++和DPC,从而验证了KNN-DPC在高维文本数据集上聚类具有更好的效果。
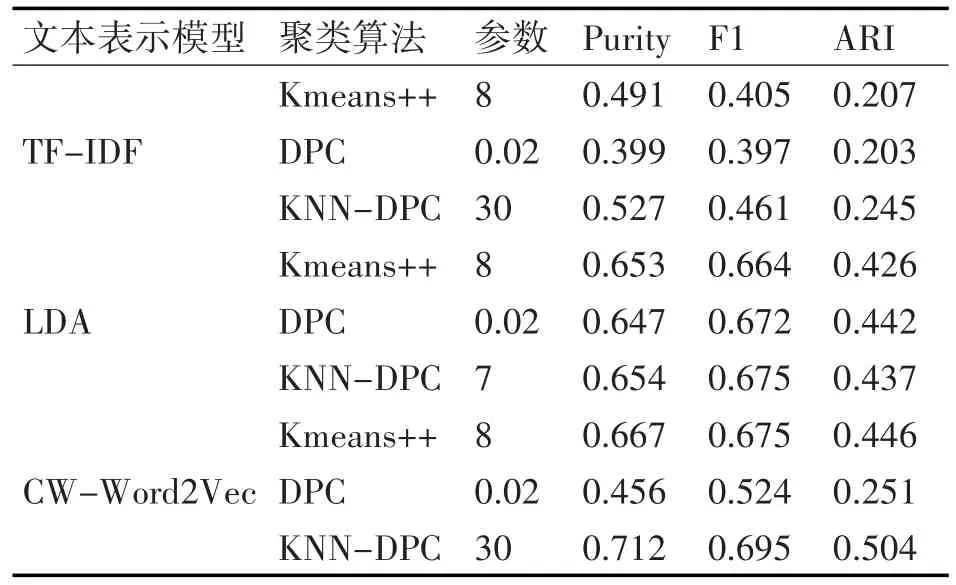
表1 搜狐新闻数据集聚类实验结果

图1 TF-IDF模型下不同聚类算法聚类结果

图2 LDA主题模型下不同聚类算法聚类结果

图3 CW-Word2Vec模型下不同聚类算法聚类结果
5 结语
本文首先基于Word2Vec提出一种选取核心词来表示新闻文本向量的方法。然后介绍了密度峰值聚类算法的主要思想和存在的问题并针对密度峰值聚类算法存在的问题提出了基于KNN改进的密度峰值聚类算法。在搜狐新闻数据集上的实验结果表明本文改进后的聚类算法的可行性以及有效性。后续工作将研究如何更好地改进算法质量降低复杂度。
