高斯-柯西变异算子优化的LSSVM模型研究*
2020-03-04徐巍巍
周 慧 王 进 顾 翔 徐巍巍
(1.南通大学计算机科学与技术学院 南通 226019)(2.中天智能装备有限公司 南通 226000)
1 引言
最小二乘支持向量机在支持向量机[1]的基础上进行优化的一种机器学习算法,能够加快学习和计算效率。采用最小二乘支持向量机(LSSVM)模型进行回归训练时,需要确定该模型中的两个参数:惩罚参数γ和核参数σ。国内外已有部分学者通过多种优化方法对该两个参数进行优化,如蚁群算法[2]、模拟退火算法[3]、果蝇优化算法[4]、遗传算法[5]、粒子群算法[6]等。
传统的种群优化算法无法避免陷入局部收敛和收敛速度慢[7~8]的问题,为了改进这些缺陷,本文提出一种基于GC变异算子的量子粒子群算法对LSSVM的参数进行优化,利用高斯变异数的局部开发能力和柯西变异数的全局探索能力,来避免优化算法的局部极值并提高收敛速度。
2 最小二乘支持向量机
SuyKens[9]提出的最小二乘支持向量机将标准支持向量机的不等式约束的二次规划问题转化为等式约束的线性方程组求解问题,从而提高了求解的收敛速度,更适合高维度大样本训练。
利用LSSVM对函数f(x)要解决的优化问题为

其中w为权向量,b为一个数,γ是惩罚参数,ξ是松弛因子;要求解决该问题,则构造拉格朗日函数,并求解得到线性方程:

K(x,xi)为核函数,一般选择泛化能力较强的径向基核函数[10],其公式为
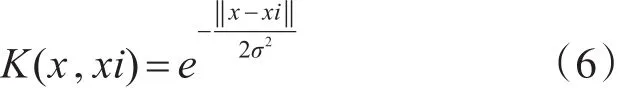
最后得到非线性预测函数:
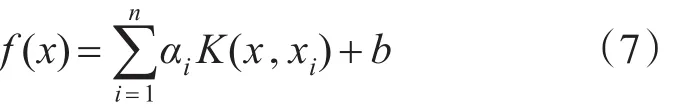
以上公式中,需要优化的参数包括σ和γ,因此要解决LSSVM的参数优化就是解决σ和γ的参数优化问题[11]。
LSSVM参数优化是LSSVM模型应用的关键问题,杨福刚[12]将LSSVM模型参数作为抗体的基因设计抗体的编码方案,利用人工免疫算法对LSSVM参数优化搜索。提出一种基于人工免疫原理的参数寻优算法,这种方法大大减少了运算量,提高了寻找最优参数的效率。陈帅等[13]将进化类算法引入最小二乘支持向量机的参数优化,能够有效地进行参数寻优,使用遗传算法和粒子群算法进行的参数寻优都取得了较好的仿真效果。张涛等[14]采用QPSO算法对LSSVM模型参数进行优化,算例表明,该算法避免了标准粒子群算法陷入局部极小值的缺陷,能在较短的迭代次数获得优于粒子群算法的最优解。本文针对最小二乘支持向量机参数优化问题,在QPSO优化的基础上,提出一种基于高斯-柯西变异算子的参数优化方法,旨在避免种群优化算法时极易出现的局部极值问题,并提高收敛效率。
3 基于高斯-柯西变异算子优化量子粒子群算法
在量子粒子群(QPSO)优化最小二乘支持向量机算法时,为了避免优化过程中的局部收敛问题,有研究者用高斯变异数[15]操作和柯西变异数操作[16]代替随机数变异操作来增加粒子的多样性。考虑到高斯变异数局部开发能力较强[17],柯西变异数具有两翼分布概率,更容易跳出局部区域,适合全局探索[18]。本文提出基于高斯-柯西变异算子的量子粒子群算法——GCQPSO算法。GCQPSO具体步骤如图1所示。

图1 高斯-柯西量子粒子优化流程图
GCQPSO算法中主要涉及的变量有pBest、gBest、Pi、mBest、GC,其中pBesti表示第i维粒子历史最优位置,gBest代表全局最优位置,Pi代表第i维粒子的局部吸引点,mBest代表平均最优位置,
步骤1:初始化粒子群,随机产生每个粒子的位置,粒子状态用波函数ψ(x)表示。

参数L的公式为

采用蒙特卡洛方程可以解得:
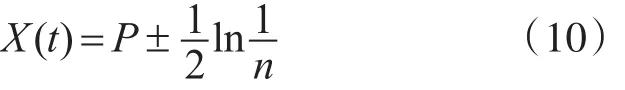
量子粒子群局部吸引点Pi位置表示为

步骤2:计算每个粒子的适应度值f(Xi),如果小于个体最优位置的适应度值f(Pi),则更新个体最优位置为Pi=Xi。
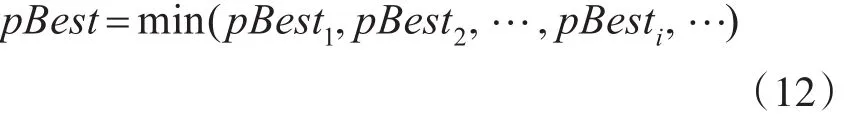
步骤3:更新全局最优位置,若个体最优位置适应度值低于全局最优位置,则更新gBest=pBest。
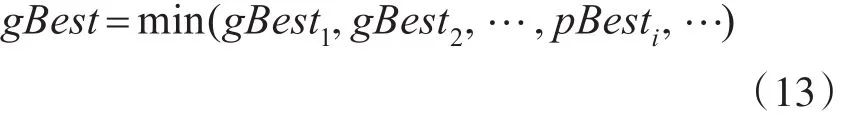
步骤4:计算平均最优位置mBest。

步骤5:对gBest和mBest进行高斯-柯西算子变异。
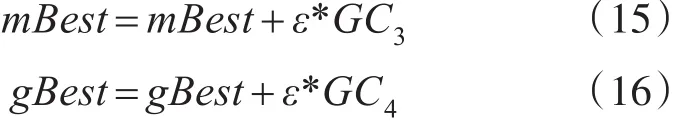
步骤6:更新每个粒子的位置。

步骤7:判断是否满足停止条件。
4 GCQPSO-LSSVM模型
本文实验数据使用江苏省某光伏电站2016年7月到2017年6月的实际运维数据,采集粒度为5min一次。实验使用的数据达到4万多条,数据进行清洗、缺失值补全、虚拟变量赋值,以及数据标准化之后可用于光伏发电量预测模型的训练。根据时点对所有的数据分类,从早晨6:00到晚上19:00,取间隔5min作为一个时点进行分类,分别建立GCQPSO-LSSVM预测模型来讨论某一时点在不同季节、不同天气特征下的发电量。在训练模型过程中,将数据的50%作为训练集,再取余下数据的30%作为测试集,其余的数据作为验证集。为了保证训练模型的准确性和泛化能力,对数据进行三折交叉验证实验。GCQPSO-LSSVM模型训练步骤如图2所示。

图2 GCQPSO-LSSVM模型训练流程图
5 实验分析
为了研究高斯-柯西变异算子对量子粒子群算法的优化效果,设计实验比较高斯-柯西优化量子粒子群算法(GCQPSO)和标准量子粒子群算法(QPSO)、高斯优化量子粒子群算法(GQPSO)和柯西量子粒子群算法(CQPSO)对LSSVM模型的优化过程和结果。实验以迭代次数和适应度函数为评价指标,进行算法对比。一般认为迭代次数越少,收敛效果越好,但仍需结合适应度函数判断,以避免局部极值干扰。
适应度函数设为均方根误差公式:

5.1 不同变异算子的优化实验设计
分别利用不同方法训练LSSVM模型,得到QPSO-LSSVM、CQPSO-LSSVM、GQPSO-LSSVM、GCQPSO-LSSVM模型。QPSO-LSSVM代表标准量子粒子群优化法优化最小二乘支持向量机。GQPSO-LSSVM代表用高斯变异随机数变异代替随机数变异。CQPSO-LSSVM代表用柯西变异随机数变异代替随机数变异。GCQPSO-LSSVM代表用高斯-柯西变异随机数变异代替随机数变异。四种优化方法的具体区别在于 P、gBest、mBest和 Xij的迭代,如表1、表2、表3和表4所示。

表1 GCQPSO迭代公式

表2 CQPSO迭代公式

表3 GQPSO迭代公式

表4 QPSO迭代公式
从表1、表2、表3和表4中可以明显看到四种优化方法的迭代方法的不同之处。QPSO的迭代方法最简单,变异因子为满足(0,1)分布的任意随机数,GQPSO的变异因子为符合高斯分布的随机数,CQPSO的变异因子为符合柯西分布的随机数,GCQPSO的变异因子为符合高斯-柯西分布的随机数。
各种变异因子的表达公式如下:
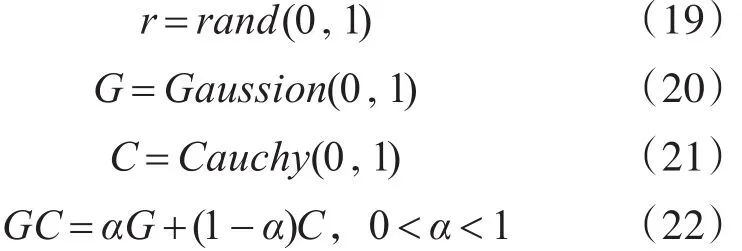
利用以上四种不同变异算子的量子粒子优化方法对LSSVM模型进行优化的过程及结果将在下一节中具体分析。
5.2 不同变异算子的优化过程分析
通过对迭代次数和适应度值来分析不同变异算子优化的量子粒子群算法。表5显示的是不同变异算子对LSSVM预测模型优化过程,其中参数包括迭代次数和适应度函数值。本模型中以均方根误差RMSE作为适应度函数,适应度函数值越小,优化效果越好;达到最小适应度值的迭代次数越少,收敛越迅速。实验迭代次数范围设置为小于200。从表5中可以看出,CQPSO迭代次数最大,适应度函数值较小,效果尚可,这是由于柯西分布变异数全局搜索能力较强,搜索空间较大。而GQPSO迭代次数较少,能较快收敛,适应度函数值小于CQPSO,效果更好。QPSO方法迭代12次就陷入局部最优,适应度函数值较大,优化效果不佳。GCQPSO迭代次数介于GQPSO和CQPSO之间,搜索空间较广,收敛速度较快,且适应度函数明显小于以上三种方法,预测精度较高。
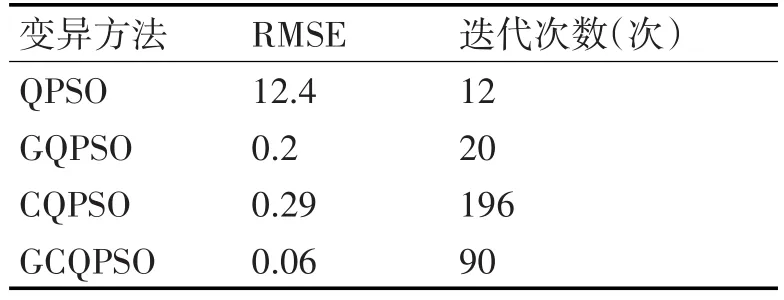
表5 不同优化算法优化过程及结果对比
从图3可以很显著看出,QPSO在迭代初期就陷入了局部收敛状态,四种方法的迭代速度、搜索空间、适应度值比较分别如下。
迭代次数比较:CQPSO>GCQPSO>GQPSO>QPSO;
搜索空间比较:CQPSO>GCQPSO>GQPSO>QPSO;
适应度值比较:QPSO>CQPSO>GQPSO>GCQPSO。
根据以上比较可以知道,量子粒子群算法的迭代次数最短,搜索空间最有限,适应度值最大,达到12以上,优化结果不理想。高斯量子粒子优化(GQPSO)算法的搜索空间介于柯西量子粒子(CQPSO)算法和高斯-柯西量子粒子(GC-QPSO)算法之间,迭代次数少于其他三种算法,适应度值介于CQPSO算法和GCQPSO算法之间。属于迭代较快,也能达到较好优化结果的算法。柯西量子粒子(CQPSO)算法的搜索空间最大,迭代次数较多,适应度值大于GQPSO算法,因此不是非常理想的优化选择。而GCQPSO算法的迭代次数介于GQPSO和CQPSO之间,搜索空间介于GQPSO和CQPSO之间,但是与迭代次数最少的GQPSO相差无几,迭代次数未超过100,但是适应度值最低,因此也是比较理想的优化方法。比较GQPSO和GCQPSO算法,GCQPSO尽管迭代次数稍微高一些,但是达到的适应度值却非常接近0,完全可以弥补迭代次数带来的损失,总体来说瑕不掩瑜,整体性能稍优于GQPSO。
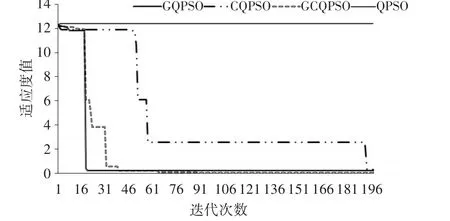
图3 不同变异算法迭代图
5.3 不同变异算子的优化结果分析
使用江苏省某光伏电站2016~2017年的实际运维数据,以时点为分界将数据分成169组数据,分别进行169组实验。分别采用GCQPSO、GQPSO、CQPSO、QPSO四种方法优化后的LSSVM建模,每个方法分别建立模型169次。图4箱线图分析四种优化方法分别进行169次实验的适应度值(即均方根误差RMSE值)的分布情况;表6分析了169次优化实验中,适应度值为四种方法中最小(即最优解)出现的次数以及百分比分布情况。

图4 各种优化方法的适应度值分布
依图4所示,针对本文的169组数据,QPSO方法优化的适应度较大,分布于0~26之间,中位数约为11.57,而GCQPSO、GQPSO、CQPSO三种方法的适应度值,分布范围依次为0~1,0~2,0~25;中位数依次为0.1,0.2,2.69。各优化方法的四分位距大小情况为GCQPSO<GQPSO<CQPSO<QPSO。
根据以上分析,GCQPSO、GQPSO、CQPSO的优化结果明显优于单独的QPSO方法,而GCQPSO、GQPSO、CQPSO三种优化方法中,GCQPSO优化的适应度值分布较其他方法更为优秀。
表6反应的是169次对比实验中,四种优化方法得到的适应度值最小的次数及百分比,即达到最优秀的优化效果的次数及次数百分比。

表6 各优化方法最优解分布情况
根据表6,显然可以看到,QPSO算法最优解为0次,即没有一次实验能够比其他三种算法优秀。GQPSO算法和CQPSO算法得到最优解的次数相等,都是28次,均占总实验次数(169)的16.57%。而GCQPSO方法得到最优解的次数为113次,占总实验次数的66.86%,相对于其他三种方法,算法的优化效果远远超过GQPSO和CQPSO方法。因此,四种算法相比,选择GC变异算子优化方法建立LSSVM模型更合理,能够在合理的迭代次数内找到最低的适应度值。
6 结语
对于本文中的数据,首先,QPSO方法迭代几次后便陷入局部最优状态,最后得到的适应度值(即RMSE值)较大。其次,CQPSO方法经过将近200次迭代才找到最优解。搜寻空间大于其他方法,收敛速度较慢。GQPSO与GCQPSO都能较快跳出局部极值,但GQPSO虽然能更快地下降到较低的适应度水平,最优解却大于GCQPSO方法寻得的最优解;GCQPSO方法在搜寻过程中搜索空间大于GQPSO,搜索过程更充分,最优值也优于GQPSO最优值。
通过上述分析,可以证实,GC变异算子优化方法在粒子搜索过程中能够寻求到搜索空间和局部极值之间一个较好的平衡点,能够保证在解空间里充分搜索,并且具备更好的跳出局部极值的能力。
