基于拍卖机制的灾害多主体合作搜救仿真研究

唐 健，郭海湘，龚承柱，诸克军

(1．西南大学经济管理学院，重庆 400715；2.中国地质大学(武汉)经济管理学院，湖北 武汉 430074；3.西安财经大学管理学院，陕西 西安 710100；4.中国地质大学(武汉)中国矿产资源战略与政策研究中心，湖北 武汉 430074)

1 引言

大规模灾害发生以后高效地开展救援工作是一个十分重要的问题。目前，关于灾害应急救援的研究成果可根据其所处阶段分为三类，“灾前准备”，“灾中应急”和“灾后恢复”。相关研究成果多集中在“灾前准备”阶段的物资储备选址[1-2]、应急预案设计[3]，“灾中应急”阶段的人员疏散[4]、应急物资调度[5-6]，以及“灾后恢复”阶段的应急能力评估[7]。应该肯定，这些研究从各个环节为灾害救援工作的开展提供了重要的理论支撑，一定程度上提高了救援效率。本文的研究内容是“灾中应急”阶段的灾后合作搜救，灾后搜救是灾害发生后复杂应急系统中的一个重要组成部分，然而，有关灾后合作搜救的研究比较匮乏。

搜救队伍间的合作救援，本质上是一个任务分配问题。关于主体间的任务分配模型较多[8]，有学者提出了基于合同网模型的任务分配机制[9-10]。也有学者将智能算法用于解决任务分配问题[11-12]，张朝潮[11]利用了遗传算法求解了消防智能体之间的任务分配问题，琚春华和陈庭贵[12]提出了扩展的蚁群劳动分工模型。现阶段发展很快的是基于拍卖的任务分配算法[11, 13-16]，Nanjanath等[15]采用了连续单一物品拍卖方案。Nair等[14]研究了集中式的组合拍卖机制和分布式的拍卖机制。Ramchurn等[17]则将任务分配用联盟形成来表示，通过F-Max-Sum算法解决这样一个分布式约束优化问题。

文中需要解决的任务分配问题是一个NP难问题[16]，可通过智能算法这样的集中式任务分配方法求解。该类方法适用于环境已知并且确定的小规模问题，但是应用于灾害现场搜救有一定的局限性，比如模型复杂性，决策延迟性等。拍卖算法这样的分布式算法用来解决任务分配效率较高，灵活性强，容错性好，非常适合于动态不确定性环境中的快速任务分配[8]。灾害现场搜救场景的动态性，复杂性以及对时效性的需求使得拍卖算法成为一种较优的选择。

针对搜救队伍在灾害现场的搜索路径，通过类似于Lév ywalks这样的随机游走模型[18-19]进行模拟。很多研究提出或者论证了Lévy walks在目标点随机分布，可重复性或者不可重复性搜索，目标点静止或运动等条件下，是较优的随机搜索策略[20-21]。胡超和李克平[22]在地震灾害中引入了Lévy Flight模型对搜索过程进行模拟，结合基于救援物资调运的合作策略，分析了不同规模的搜救队伍配置对救援效率的影响。

现有的研究大多只囊括了伤员的搜索，或者只研究了合作救援，两者集成研究的较少。不难看到伤员的搜索本质上是路径规划与随机游走模型，合作救援的模型实际上是一个任务分配问题，在救援过程中，两者往往是密不可分的。

本文研究的是一个基于随机游走的伤员搜索与合作救援的集成问题。构建了一个包含伤员和搜救队伍的多Agent灾害环境，假定被困伤员生存概率会随时间增加依据特定函数发生变化[22-23]，用改进后的Truncated Lévy walks[20]模型对搜救队伍的搜索行为进行仿真，提出了基于分布式拍卖机制的合作救援方案。这里以某滑坡灾害频发地区为例进行仿真，研究了该搜救方案对救援效果的影响，并将其与基于F-Max-Sum算法的合作救援机制进行对比。最后对所提出的搜救方案的鲁棒性和敏感性进行了分析。

本文与其他同类研究的主要区别在于：

(1)采用多主体仿真方法构建了灾害的搜索救援环境，与传统救援模型相比，可以更好的体现灾害场景的非线性性、动态性和复杂性。

(2)将搜索与救援结合起来进行研究，用Truncated Lévy walks模型模拟搜索行为，更适用于灾后的环境特点，并改进了模型中参数，增加了模型灵活性。

(3)采用拍卖机制模拟了搜救队伍间的合作关系，以整体最优为目标，缩短了救援时间，提高了救援效率。

2 多主体模型描述

2.1 模型概述

模型包括两类主体，分别是伤员Agent和搜救队伍Agent。灾害发生后，掩埋点在灾害区域中随机分布，每个掩埋点的掩埋程度不同，伤员Agent散落在不同的掩埋点中，每个掩埋点中可能存在一个或多个伤员Agent。搜救队伍Agent在受灾区域内进行搜索，当搜索半径内存在伤员Agent时，搜救队伍Agent能以一定概率发现它，发现伤员的搜救队伍Agent成为拍卖者，合作范围内的其他搜救队伍Agent成为竞拍者，当需要合作时，拍卖者与竞拍者通过Agent间交互机制实现信息传递，包括伤员掩埋点坐标，掩埋情况等信息，合作达成后，针对该点展开救援，如图1。

图1 灾害救援多主体仿真逻辑模型

2.2 研究假设

假设1(效率累加假设)：所有搜救队伍的人员结构组成相同，救援能力相同，多支搜救队伍合作救援时效率累加。

假设2(信用假设)：竞拍者针对某项任务进行报价时，不存在虚假报价，即报价反映了对该任务难易程度、紧迫程度的真实评价。

2.3 伤员(Agent)属性

伤员Agent的基本属性有“掩埋程度vrubble”、 “掩埋点坐标vxy” 和“受伤程度vsi”。其中，

掩埋程度vrubble表示伤员进行救援的难度，同一个掩埋点下的伤员掩埋程度vrubble相同；

掩埋点坐标vxy表示伤员在灾害发生后被掩埋的具体位置。

受伤程度vsi有四个取值，分别为“死亡”，“重伤”，“轻伤”，“无受伤”，具体取值由专业人员根据掩埋者的意识，呼吸，体温等生命体征予以判断。下文会将受伤程度每个取值所占的比例与灾害情景结合起来，并分为“极严重”，“严重”和“普通”三种情景进行分析。

2.4 搜救队伍(Agent)行为规则

搜救队伍Agent主要参数有 “搜索半径sr”、“最大转动角度sa”、“救援速度srubble”、“合作范围sc”、“移动步长sl”、“移动方向sθ”。其中，搜索半径sr表示搜救队伍当前位置的最大搜索范围；最大转动角度sa表示搜救队伍下一步转动方向的最大范围；救援速度srubble表示的是每支搜救队伍在确定伤员的位置以后，抢救伤员的速度；合作范围sc表示只在半径为sc的圆形区域内的搜救队伍才能合作；搜救队伍依据特定的概率分布分别选择移动方向sθ和移动步长sl，然后沿着选定的方向sθ移动相应的距离sl，直至在搜索半径sr内搜索到目标，搜索一个步长后，重新选择下一步的移动[18]。

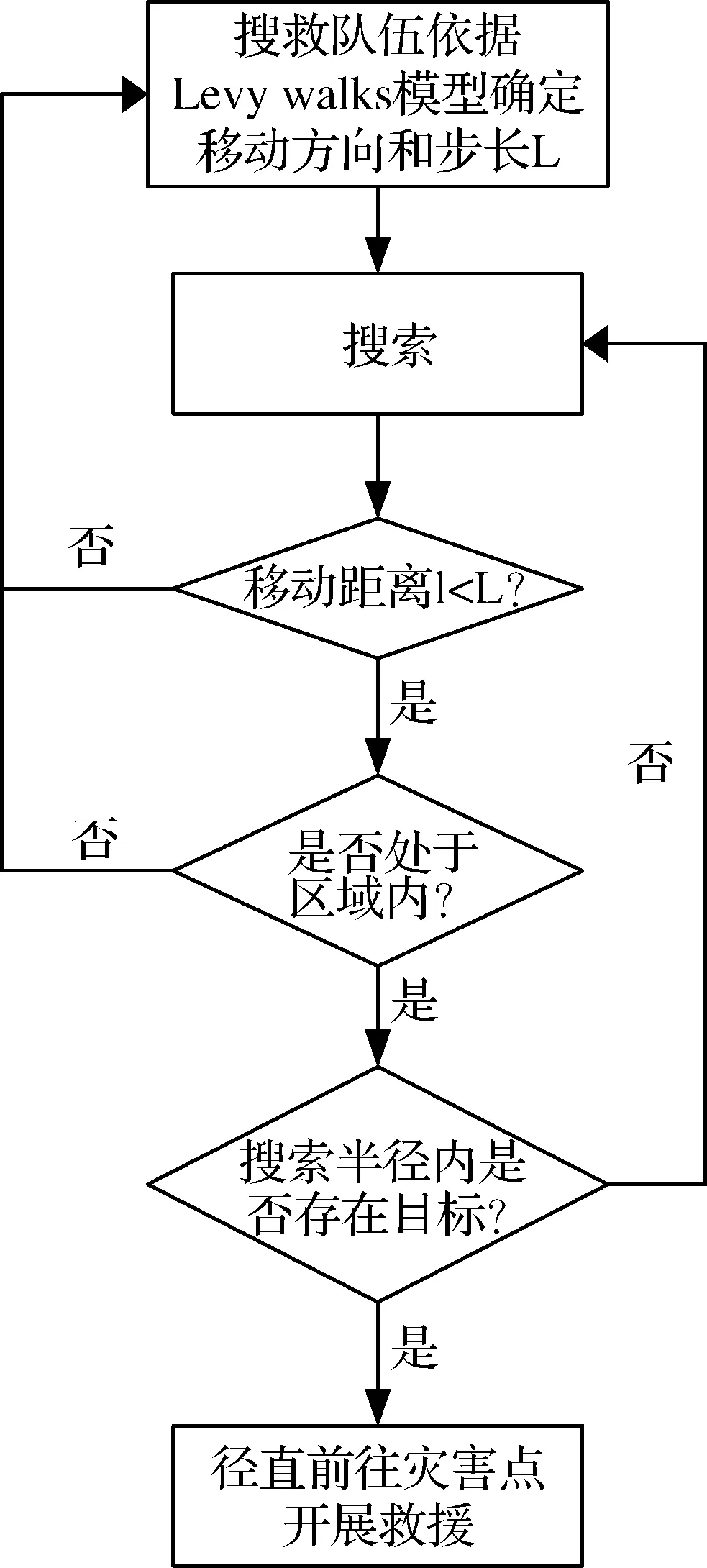
图2 搜救队伍搜索方案

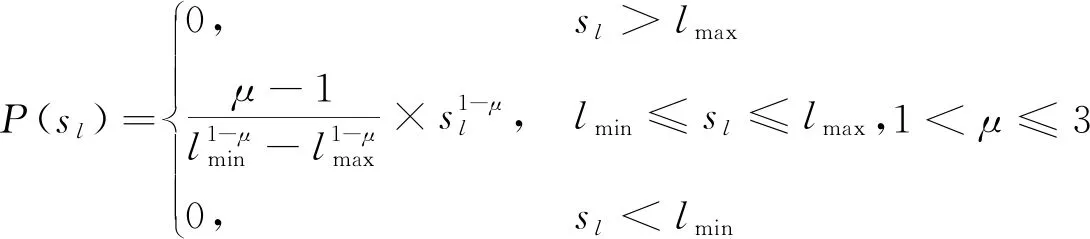
(1)

滑坡灾害现场中基本全部覆盖着泥土碎石，初期救援队伍难以获得伤员掩埋位置的准确信息，Lévy walks比较适合对搜索行为进行模拟。本文采取改进后的Truncated Lévy walks对搜索过程进行仿真，可以对搜索过程中最小、最大步长施加一定的限制，其步长的概率密度函数如式(1)[20]，其中，μ是特征指数，lmin和lmax分别表示该随机游走模型中的最小和最大步长，由于搜索半径sr内的目标可以被搜索者发现，因此该模型中的步长sl至少应大于搜索半径sr，即lmin=sr，最大步长则受到环境大小的限制[20, 24]。在仿真中，通过反函数法(Inverse Transform Sampling)得到抽样函数：

(2)

Lévy walks模型中搜索的移动方向sθ服从U(0, 2π)分布，对每一个方向都给予相等的可能性，但是在文中接下来用的随机游走模型中，移动方向sθ服从均匀分布，sθ～U(0,sa)，将sa作为一个可控制的参数进行研究。

搜救队伍的具体搜索方案如图2所示。

3 合作救援机制

本研究中每支搜救队伍由大致相同的人员组成，每支队伍都包含了搜索人员、破拆顶撑人员、医疗人员等，每支队伍都有独立完成救援任务的能力。队伍内部不同类型的救援人员之间有合作，即队内合作；不同搜救队伍之间也有合作，即队间合作。队内合作是既定的，本文研究队伍间基于拍卖机制的合作。拍卖作为一种基于市场的任务分配机制，效率较高。该研究中搜救队伍之间通过分布式拍卖实现救援任务的分配，过程中主要有两种角色，任务的发布者Ai和任务的响应者Bj，分别相当于拍卖中的拍卖者和竞拍者。模型中主要符号及定义如表1所示。

表1 模型中主要符号及定义

3.5 拍卖者

当搜救队伍发现目标后，即成为拍卖者Ai，合作范围sc内的其他没有发现目标的搜救队伍成为任务的竞拍者Bj。拍卖者Ai先对Ti掩埋情况进行评估，假设需要在时间tneed内完成任务，则确定完成任务Ti需要的搜救队伍数量为

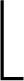
(3)

当ni>1时，拍卖者Ai通过Agent间通信的方式在一定范围内发布拍卖任务Ti，收到拍卖消息后，竞拍者Bj根据自身所处的状态确定投标价格pij。拍卖者选取投标价格比较高的前ni-1个竞拍者。一轮拍卖有一定的时间限制tl，当拍卖时间超过tl或者拍卖目的得到满足，则该轮拍卖结束，先开始救援工作。在救援过程中，若拍卖目的未能满足，再次发起拍卖。

3.2 竞拍者

3.2.1 竞拍者的效用评价

竞拍者参加任务Ti的效用ui通过救援任务的救援优先级评价结果进行衡量，救援优先级越高，救援越具紧迫性，效用越大。任务Ti的救援优先级评价采用模糊综合评判法进行分析。

评价因素集用集合Z表示，Z={z1,z2,…,zq}，其中za(a=1, 2,…,q)表示第a个评价因素，q是因素数。确定评价集，一般选取3-5个评价级别，用集合V表示，V={v1,v2,…,vp}，其中vb(b=1, 2,…,p)表示第b个评价级别，p是评价级别划分的数量。

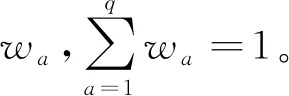
H=WR=(h1,h2,…,hp)

(4)

3.2.2 竞拍者的成本分析

模型中考虑了成本，是为了根据伤员的位置分布、掩埋情况的轻重缓急合理分配救援力量，减少搜救队伍浪费在路上的时间，提高整体救援效率。这里主要涉及到两类成本，直接成本和机会成本。与传统的成本含义不同，直接投入成本cij主要由搜救队伍离掩埋点的距离dij和完成救援任务所需时间tij决定，即

cij=f(dij,tij)

(5)

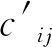
(6)

3.2.3 竞拍者的投标策略

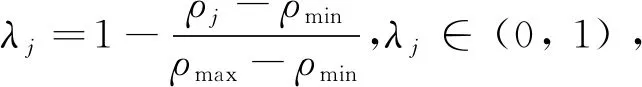
(7)

3.3 拍卖机制的动态调整

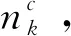
4 仿真分析——以滑坡灾害为例

为了研究文中基于拍卖机制的合作救援方案的有效性，先将其与非合作救援进行对比，然后与基于F-Max-Sum[17]算法的救援方案进行比较。F-Max-Sum也是一种分布式算法，在Max-Sum算法的基础上进行了改进，适用于解决类似的动态任务分配问题，并且性能出色。F-Max-Sum算法先将需要解决的问题转化成因子图的表达形式，通过不断对因子图中变量节点和函数节点之间信息传递的值进行迭代，直至收敛或者迭代了一定次数。

4.1 参数设定

这里以滑坡灾害为例进行分析，采用R和NetLogo软件进行计算与仿真。仿真模型中灾害区域取自某一滑坡灾害频发地区，将该区域的GIS矢量数据文件导入仿真平台NetLogo，界面如图3所示。该仿真中主要利用到了该区域的道路信息，如图4所示，其中最粗的线条刻画了该区域道路分布情况。一定数量的伤员散落分布在区域内若干个掩埋点中。仿真步长ticks以min 为单位，当现场没有存活的伤员时，仿真结束，每次仿真周期最长为72 h。

图3 NetLogo仿真平台界面

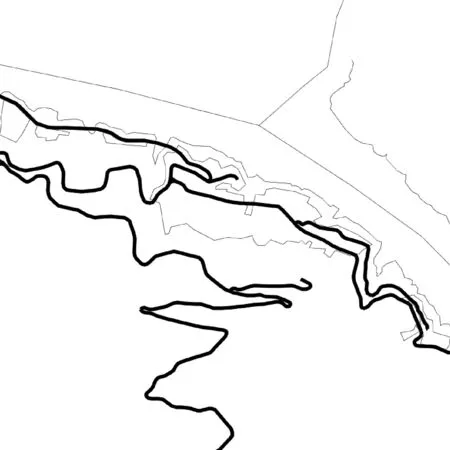
图4 灾害区域的矢量格式地图

结合近几年滑坡灾害的伤亡数据统计结果(来源：http://www.emdat.be/database)，假设不同情景下滑坡灾害受伤程度的具体分布如表2所示，如在“极严重”情景下，伤员死亡比例40%，重伤比例25%，轻伤比例15%，无受伤比例20%。

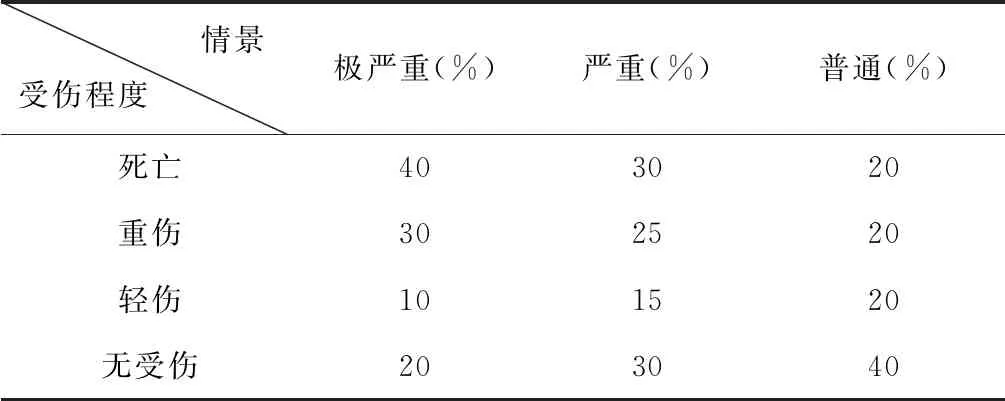
表2 不同情景下的受伤程度分布

输入变量包括：每个掩埋点的伤员人数ns～U(1,3)；每个伤员的受伤程度vsi根据表2进行初始化；每个掩埋点的压埋情况vrubble～N(120,30)；掩埋点限定的挖掘时间tneed=30；搜救队伍数量m=40，均匀分布在灾害区域的周围；搜索速度为3m/min；搜索半径sr=3m；救援速度srubble=0.5；移动步长sl根据式(2)确定，其中参数μ=2；移动方向sθ～U(0,π)；当搜索半径内存在伤员掩埋点时，每一步仿真搜救队伍能以一定概率发现它，假设概率prob=20%；合作范围sc为40 m；每一轮拍卖的时间限制tl=3 min。

救援任务优先级评价的影响因素主要由“压埋人员”和“救援难度”两类因素构成[25]，在此分类下，相关研究中考虑到的具体影响因素有掩埋人数，房屋结构，倒塌方式[25]；掩埋深度，伤员生理状况，建筑物类型[26]等。结合滑坡灾害的现场环境特点，考虑了数据的可获得性，最终选取掩埋人数、受伤严重程度两个评价标准以衡量“压埋人员”因素，选取掩埋程度以衡量“救援难度”。

掩埋程度体现出救援难度；掩埋人数即该点被掩埋伤员数量；受伤严重程度为该点被掩埋伤员严重程度之和，每个伤员受伤严重程度值“3”，“2”，“1”和“0”，分别对应受伤程度“重伤”，“轻伤”，“无受伤”和“死亡”。评价标准如表3。救援优先级研究中评价标准的权重并不是唯一确定的，多是通过专家评分法确定[25]。通常“压埋人员”因素的权重应大于“救援难度”，在该前提下，综合考虑专家的意见和计算的简化，本文将权重初步设定为W=(1/3, 1/3, 1/3)，即“压埋人员”和“救援难度”的权重比为2∶1。

表3 掩埋点优先级评价准则

针对每个影响因素za，采用半梯形分布函数计算隶属于每个评价级别vb的程度rab，即隶属度rab。以掩埋程度z1，评价级别v1“优先”为例，计算隶属度r11，如下所示：

(8)

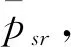
生存概率vsp是与受伤程度vsi相关的一个变量。被困于掩埋物中的伤员，在未被救出之前，生存概率会随着时间流逝逐渐减小[22-23]，并受伤员的受伤类型和所处的环境影响。滑坡与地震灾害中被掩埋伤员的生存概率亦受以上相同因素影响，考虑到两种灾害之间的联系，被掩埋伤员所处环境和受伤类型的相似性，本文拟借鉴地震灾害的生存概率函数。假设滑坡灾害中被掩埋伤员生存概率vsp随时间变化的程度如式(9)所示[23]，其中，vsp-hi，vsp-si和vsp-ni分别表示重伤人员，轻伤人员，未受伤人员的生存概率，t表示受困时间(单位：h)。

vsp-hi=e-(t/3.324)3.71

vsp-si=e-(t/26.59)3.71

vsp-ni=e-(t/66.48)3.71

(9)

4.2 仿真结果

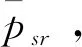
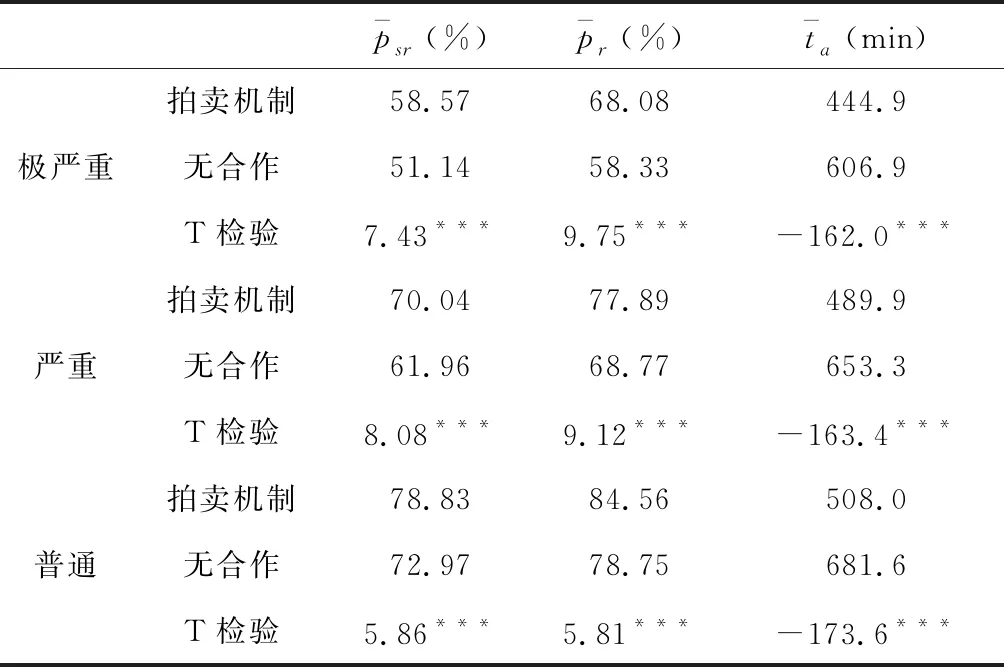
表4 不同情景下两种救援方案的仿真结果对比

注：“*”、“**”、“***”依次表示显著性水平为0.1、0.05、0.01时检验结果显著。

表5是基于拍卖机制与基于F-Max-Sum算法的两种合作救援方案的仿真结果对比，前者的部分指标在部分场景下略优于后者并通过了T检验，说明在统计上是显著的，另外部分指标则并无显著差异。表明在该案例中，基于拍卖机制的合作救援方案与知名的F-Max-Sum算法相比，其性能并无逊色，甚至部分指标略优于后者，并且其优势之一在于计算过程的低复杂性。F-Max-Sum算法在迭代过程中，函数节点需要遍历周围变量节点的各种组合，会消耗大量时间，尤其当协作集较大，即待救援任务周围可调配的救援队伍较多的时候，耗时更久。另外，F-Max-Sum最初是为具有计算功能的设备之间的合作而设计，如机器人、传感器等，将其直接运用于灾害现场搜救队伍之间的合作存在适应性问题。

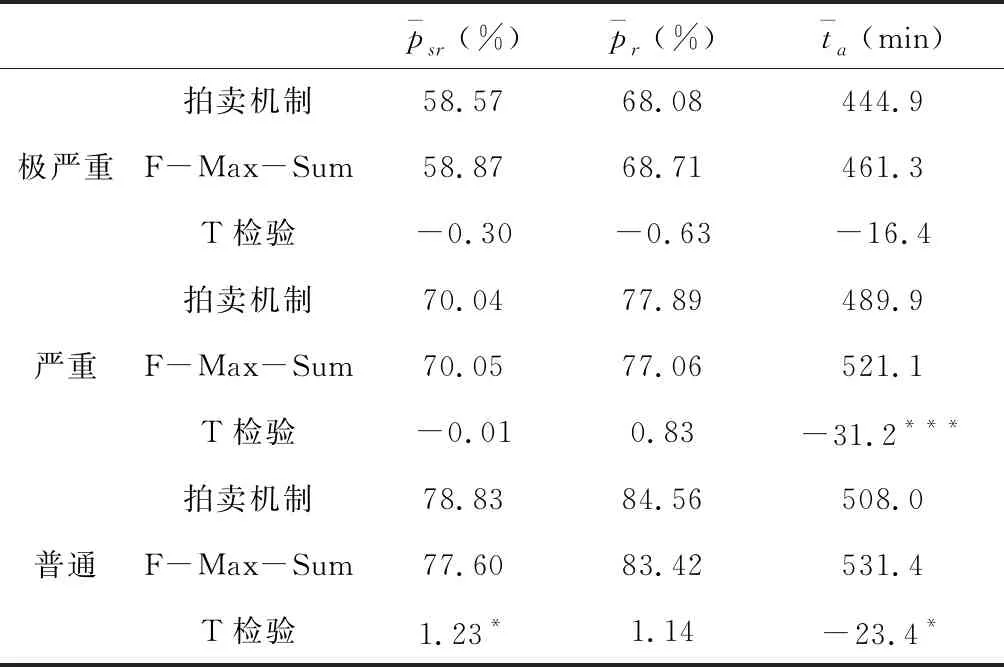
表5 基于拍卖机制与基于F-Max-Sum算法的两种救援方案仿真结果对比

注：“*”、“**”、“***”依次表示显著性水平为0.1、0.05、0.01时检验结果显著。

图5-7是分别进行200次仿真后，三种不同情景下，约1600个仿真步长内基于拍卖机制的合作救援与非合作救援过程中相对生存概率、伤员救出比例随时间变化的平均情况。横坐标表示仿真中每个时间点，左边纵轴表示相对生存概率，次纵轴表示伤员救出比例。可以看出，救援的初始阶段，相对生存概率下降较快，随着救援工作的开展，约在200min以后，相对生存概率下降速度放缓，并且整个过程中合作救援的相对生存概率一直高于非合作救援。

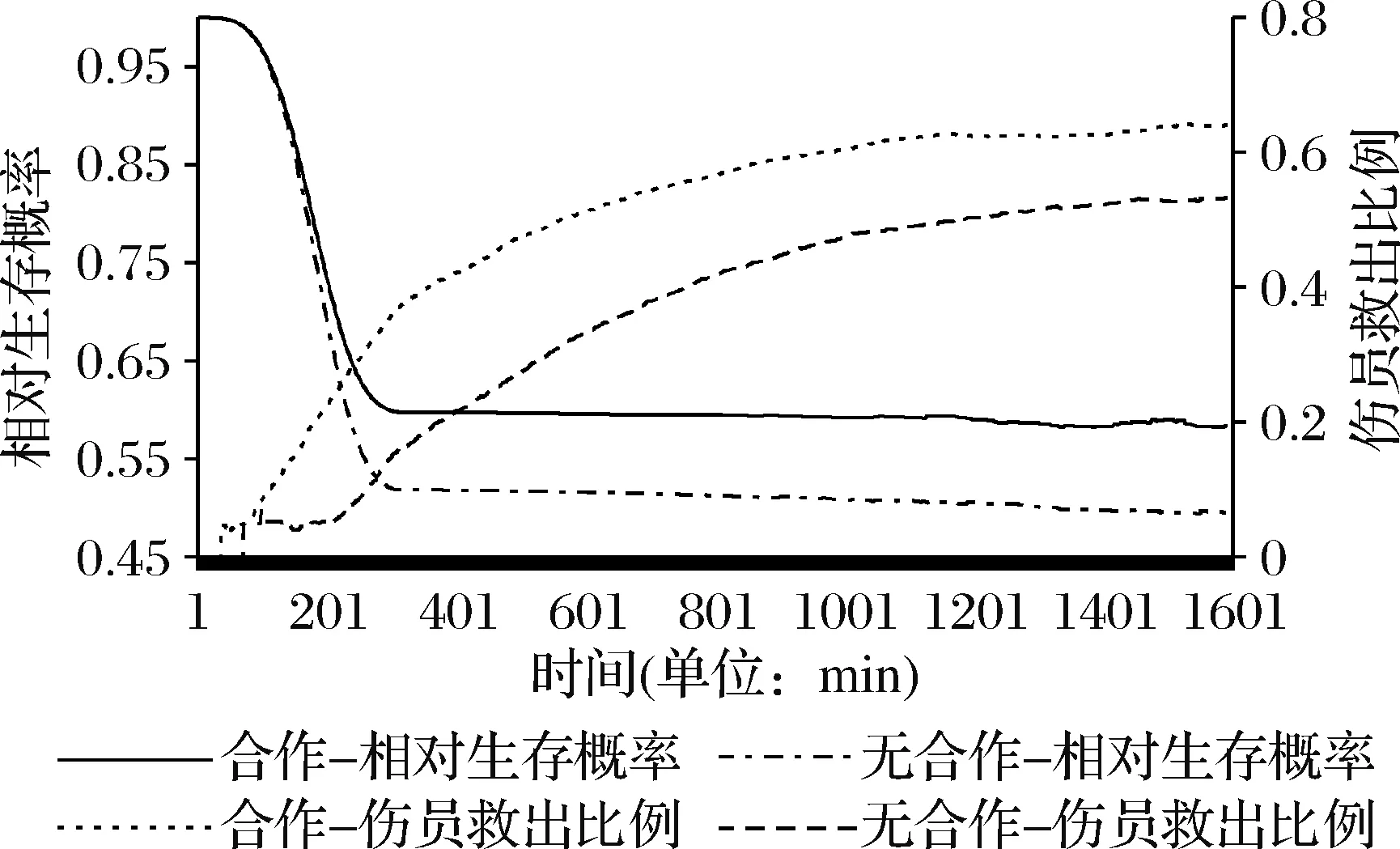
图5 “极严重”情景下相对生存概率与救出率的变化

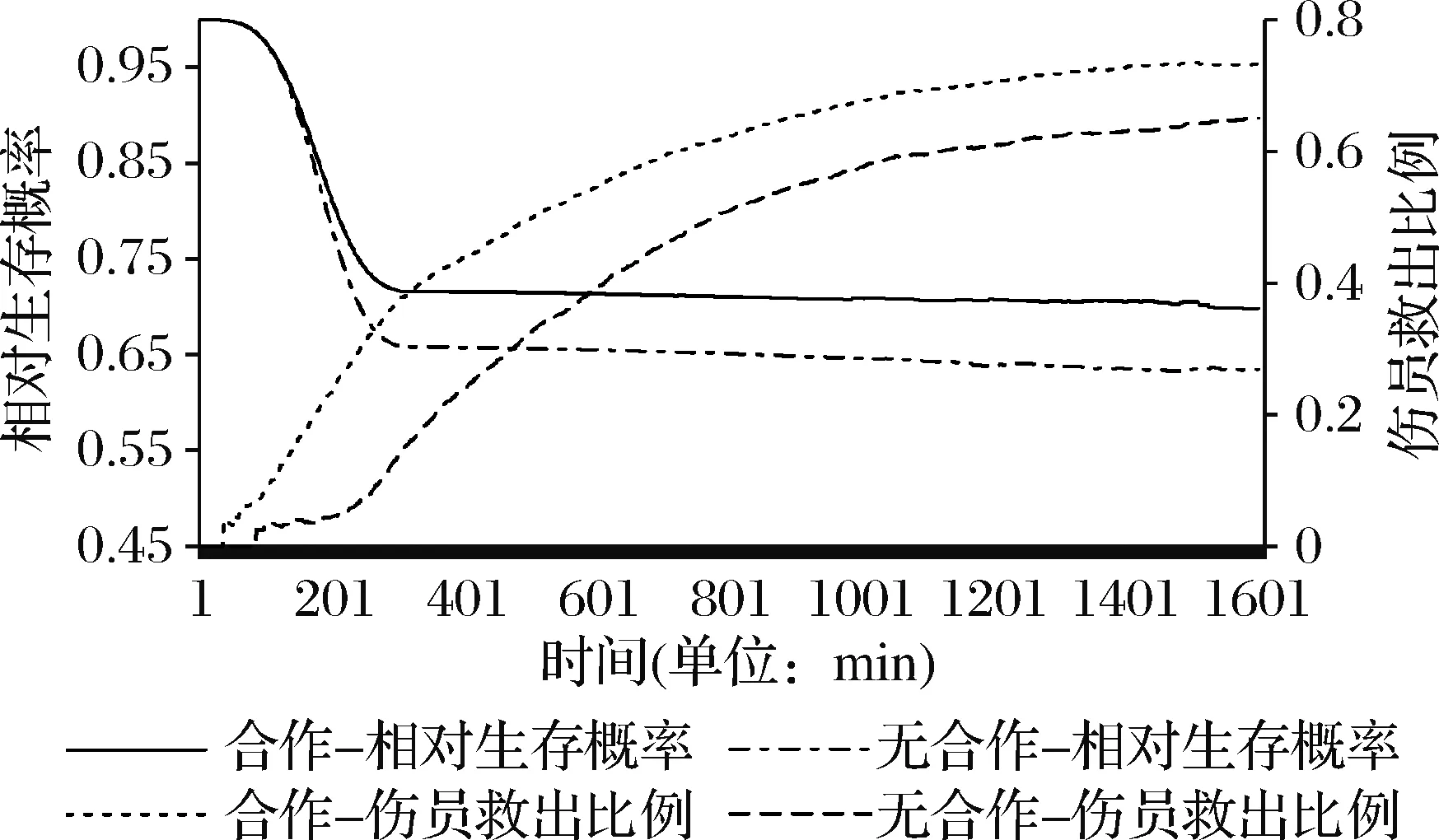
图6 “严重”情景下相对生存概率与救出率的变化

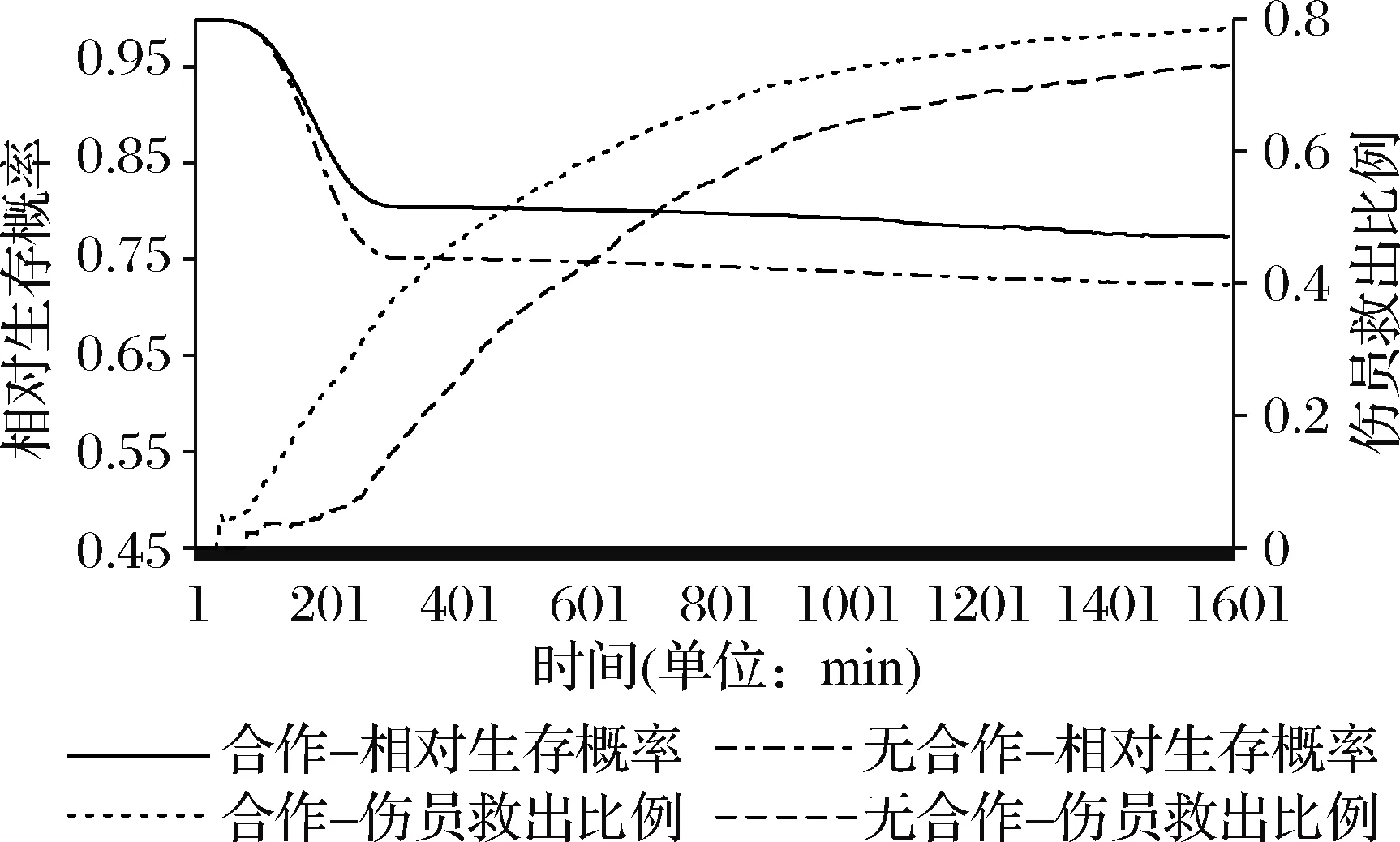
图7 “普通”情景下相对生存概率与救出率的变化

以上仿真结果表明，基于拍卖机制的合作救援方案相比非合作救援，相对生存概率同比提高8.0%～14.5%，伤员救出比例同比提高7.4%～16.7%，各掩埋点平均救援完成时间同比减少25%～26.7%，并且随着灾情的严重程度增加，救援效果提高越趋于明显。

5 模型评价

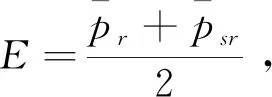
5.1 鲁棒性分析

鲁棒性描述的是救援效率会在多大程度上受到一些意外因素的影响，当改变模型的一些初始设定后，然后进行多次仿真，通过以下指标对模型的鲁棒性进行评价[27]：

(10)

其中,(xi,Ei)指被研究的仿真参数设定值和对应的救援效率值。LRS值越显著，绝对值越大，说明该参数对救援效率的影响越大。

进行鲁棒性分析时，要研究的影响因素包括搜索半径sr，合作范围sc。当搜救工作发生在晚上，或者因为其他某些不可抗力，搜索半径必然会发生变化。在受到某些干扰因素时，如环境恶劣、受通讯条件所限，合作范围的减小是不可避免的。图8与图9是基于拍卖机制的合作救援方案的鲁棒性分析结果。

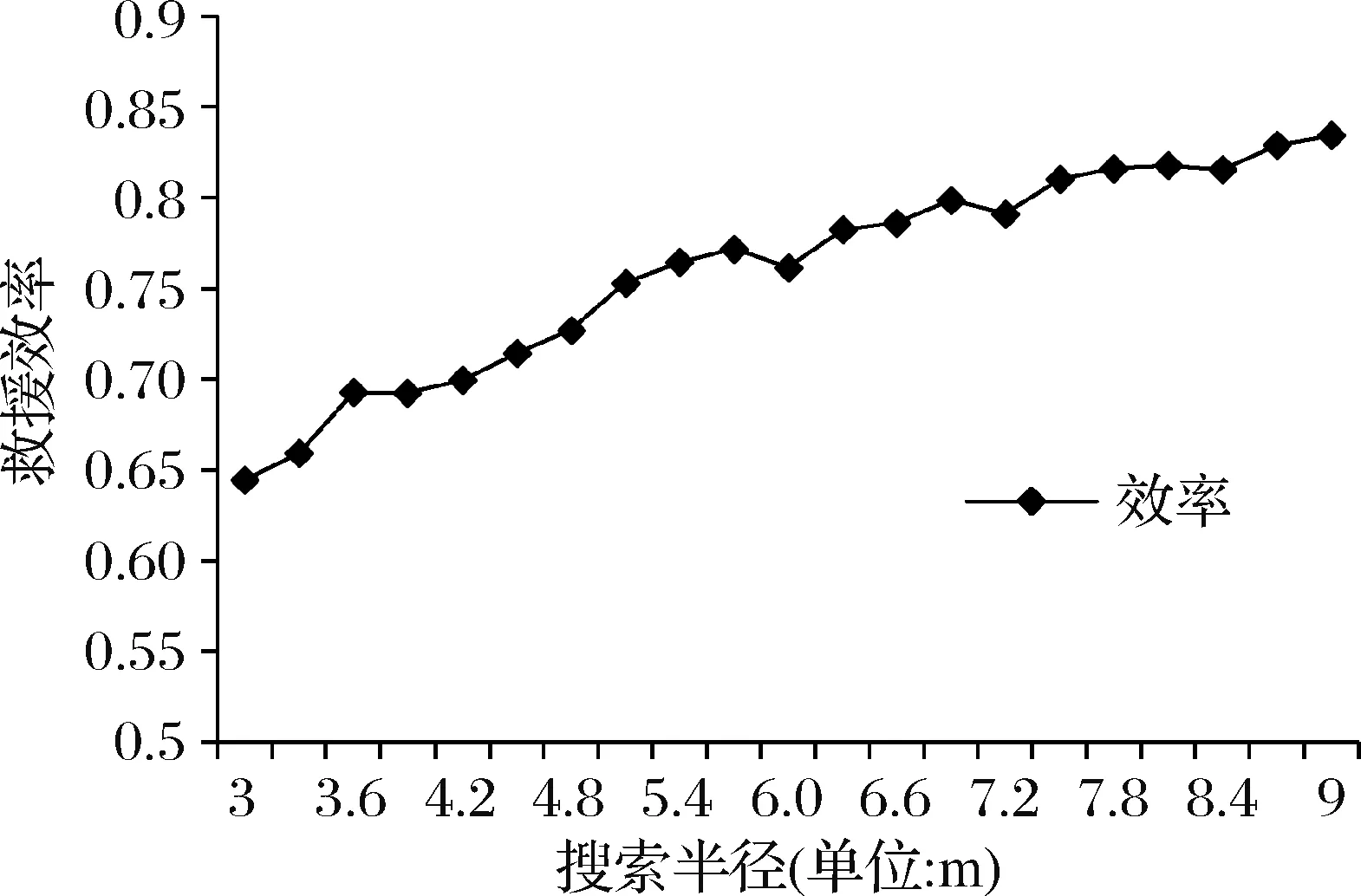
图8 搜索半径对救援效率的影响

图8中，搜索半径sr从3m以0.3m的间隔递增至9m，一共21轮仿真，每轮仿真重复200次，纵轴表示救援效率，横轴表示每轮仿真的序号，在其他参数不变的情况下，随着搜索半径的变大，救援效率明显改善。其鲁棒性指标LRS值为0.03，并在0.01的显著性水平下是显著的。表明搜索半径的变化对救援效率有显著的影响，这种影响呈线性关系，即当搜救工作发生在晚上，或者因为其他不可抗力，导致搜索半径变小，那么救援效率会降低。

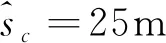
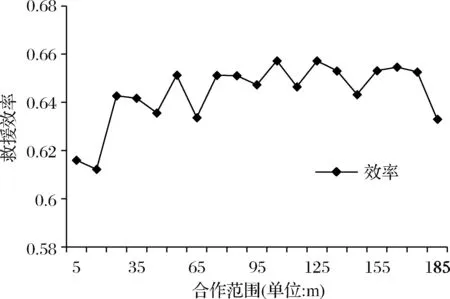
图9 合作范围对救援效率的影响

5.2 敏感度分析

仿真模型中的不确定性，体现在一些模型参数的选取上，这些参数在多大范围内的改变会对仿真结果产生影响，则需要进行敏感度分析。主要研究的参数有最大转动角度sa和掩埋点限定的挖掘时间tneed。图10与图11为基于拍卖机制的合作救援方案敏感度分析结果。

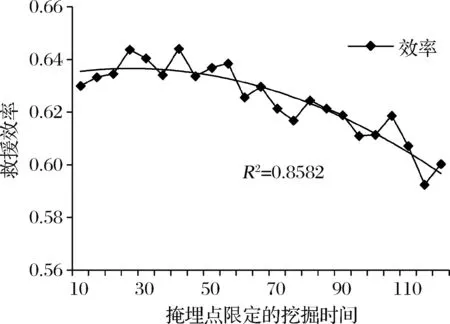
图10 掩埋点限定的挖掘时间与救援效率之间的关系

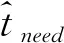
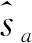
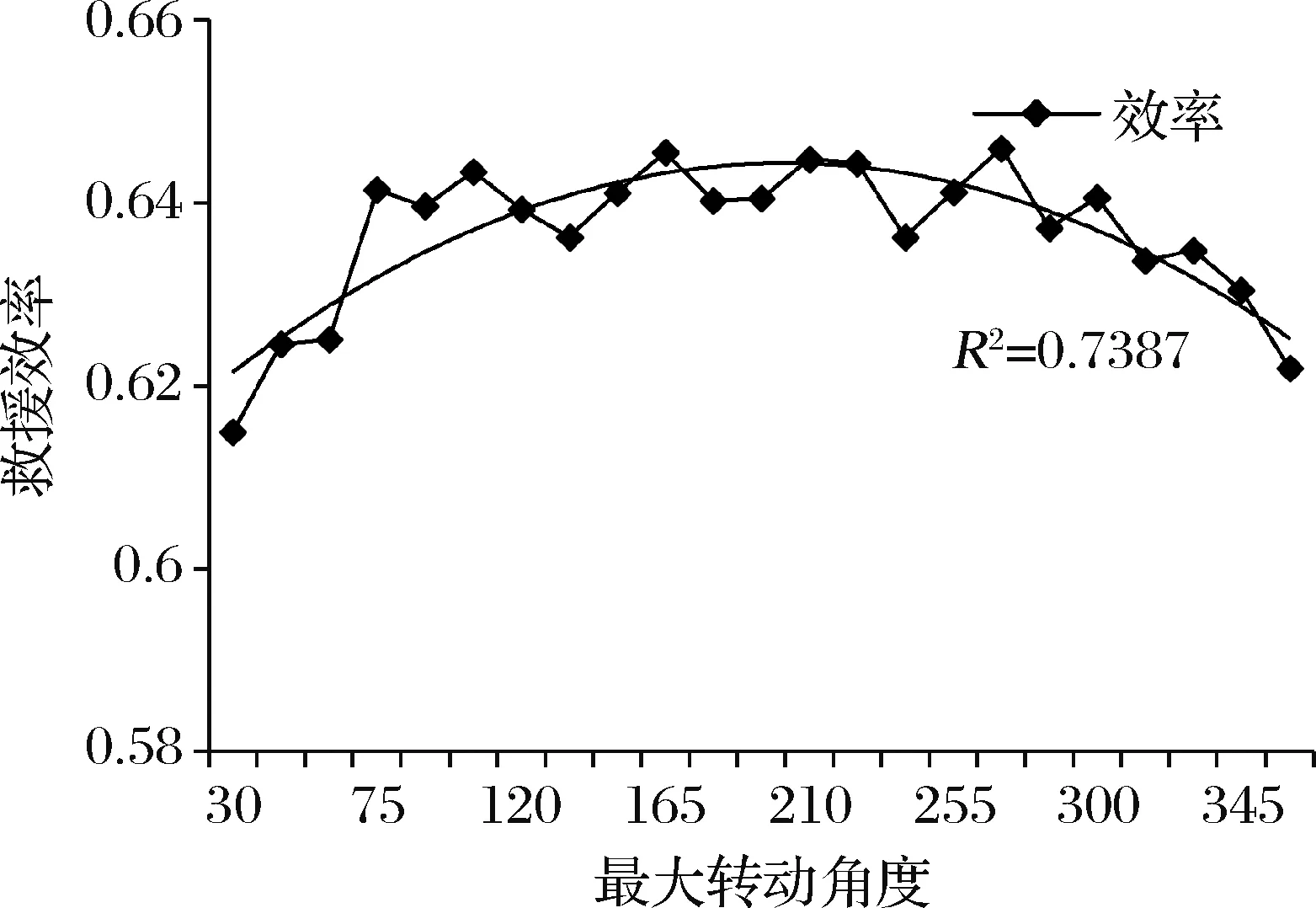
图11 最大转动角度与救援效率之间的关系

6 结语

灾害救援过程中，不断的有新的掩埋点被发现，同时又不断有掩埋点完成救援，整个系统状态在不断快速变化。本文所要解决的就是在这样一个动态的灾害环境中，救援队伍间针对某一个具体掩埋点(救援任务)如何形成合作关系的问题，通过制定合理的灾后合作搜救方案，在这种不确定性的灾害环境中寻求较优的救援效果。以某滑坡灾害频发地区的灾害搜救为例的仿真结果证明了所提出的基于分布式拍卖机制的合作搜救方案的有效性，与类似的F-Max-Sum算法对比，性能并不逊色，并且该合作机制的低复杂度，高效性使其更适用于应急决策过程的要求。

模型评价部分的鲁棒性分析结果表明外部环境变化导致的搜索半径变化会对救援效果产生影响，但合作范围的扩大并不会对救援效率有明显影响。因此，当外部环境恶化时，只要合作范围不小于一个临界值，救援效果就比较稳定。敏感度分析结果表明最大转动角度和掩埋点限定的挖掘时间两个参数均存在最优值，使得救援效率最高。即在现场搜救过程中，搜救队伍不仅需要确保搜索范围的全面性，还需要权衡保证自己的前进方向是往前的，减小搜救过程的随意性。在合作救援时，针对每个掩埋点需要分别确定合适的队伍需求数量，以保证合作救援的整体高效性。

本文提出的基于分布式拍卖机制的合作救援方案可以运用到其他类似的灾害救援中，解决其中的搜救队伍间合作问题，以上结论基本适用，但是值得一提的是，一些参数的具体取值可能会因为灾害场景的不同而有区别。比如上面提到的合作范围临界值，这个临界值在不同的灾害场景下，比如不同的搜救队伍数量、不同的受灾区域面积等，可能会存在差异。同样地，敏感度分析中的两个参数的最优值确定是一个折中、权衡(Trade off)的过程，参数取值的增加或者减小均存在利弊，不同的灾害场景中，权衡结果有可能不一致，因此决策者需要根据实际灾害场景做出选择。在未来的研究工作中，需要分析这些重要参数的取值主要受到哪些因素的影响，并挖掘其中的关系，以辅助救援指挥中心更高效快速地作出决策。另外，仿真中需要注意参数的校正问题，但是实际数据的稀缺性限制了我们使用传统的方法进行校正，接下来将注重救援案例数据的收集，通过新的方法对参数进行校正，以提高模型对实际问题的适用性。