二维网格型粗粒度可重构系统乘法器和全加器设计与验证
2020-03-02林谊东陈乃金
林谊东,陈乃金,2
(1.安徽工程大学电气工程学院,安徽芜湖 241000;2.安徽工程大学 计算机与信息学院,安徽芜湖 241000)
0 引言
随着计算机技术的不断发展,该领域对处理器性能的要求也越来越高.可重构计算系统因自身结构及性能等特点已被应用在较多领域.该系统功能由配置字来决定,这使得其在处理不同的算法和运算时具有灵活性;而独特的处理器结构设计通过算法将运算参数映射到可重构系统中进一步加速.在面对密集运算时,可重构系统的性能尤为突出,相比较通用处理器避免了处理器在复杂运行过程中性能的损失同时也弥补了专用集成电路计算模式不可再塑、高成本、高时耗等问题.由于作为一种新型的计算系统其性能与设计结构、配置信息、映射算法等都有紧密联系,因些在面对不同领域的不同运算需求时可重构计算系统都需要对整体的架构、配置、算法进行灵活的调整以获得在处理特定运算时有更高的性能.
1 相关工作
粗粒度可重构系统具有高的计算性能和低的功耗消耗,已在各个领域内被广泛运用[1],近年来相关典型研究阐述如下:文献[2]提出一种多目标优化映射算法,与层贪婪映射算法相比,平均执行总周期降低了8.4%和5.3%,与分裂压缩内核映射算法相比,降低执行周期20.6%和21.0%.文献[3]针对粗粒度单元阵列流水映射问题,设计三种行流水阵列通用的流水映射算法,与多目标优化映射算法相比该算法消耗总时延平均节省了4.0%(RCA4*4)和4.3%(RCA8*8). 文献[4]提出一种基于深度优先贪婪搜索划分算法,与现有的簇划分,簇层次敏感两种划分算法相比,显著的改善了硬件任务的划分成果,且运行开销没有明显增加.文献[5]基于粗粒度行并行可重构架构,提出一种行列剪枝映射算法,与放置路由算法相比执行时间减少了15.7%(RCA4*4)和29.8%(RCA5*5),从而验证映射算法有效性.文献[6]针对FPGA实现网络功能提出了一种可重构流水线模型,该模型实现了多种网络功能,提高资源利用率.文献[7]提出一种基于大整数乘法(Schonhage-Strassen,SSA)的768 Kbit大整数乘法器硬件架构,实现运算时间比CPU平台上的运算大约有8倍的加速.文献[8]提出一种运算精度与运算器数量可配置的并行浮点向量乘法运算单元,提高了FPGA资源利用率与运算吞吐率,同时具有高度的可移植性与通用性.文献[9]提出一种适合于FPGA的低功耗多路选择器设计方法,与传统多结构多路选择器相比,在保证其他性能的前提下,功耗降低约28.97%.文献[10]设计了基于多层次FPGA的主从式非易失性NVM(non-volatile memory)控制器,并完成适用于该架构的硬件原型设计,实现了测试同类型多片NVM协同工作,也对混合NVM存储管理方案验证.文献[11]提出一种开源处理器综合实现方法.
然而上述文献均没有对网格型粗粒度可重构计算体系结构(grid coarse grained reconfigurable architecture,GCGRA)模块部件仿真,针对这个问题,本文进行了研究,具体表述为对全加器、乘法器的动态功耗、结温、I/O等参数进行了综合分析和比较.
2 网格型粗粒度可重构计算系统简介
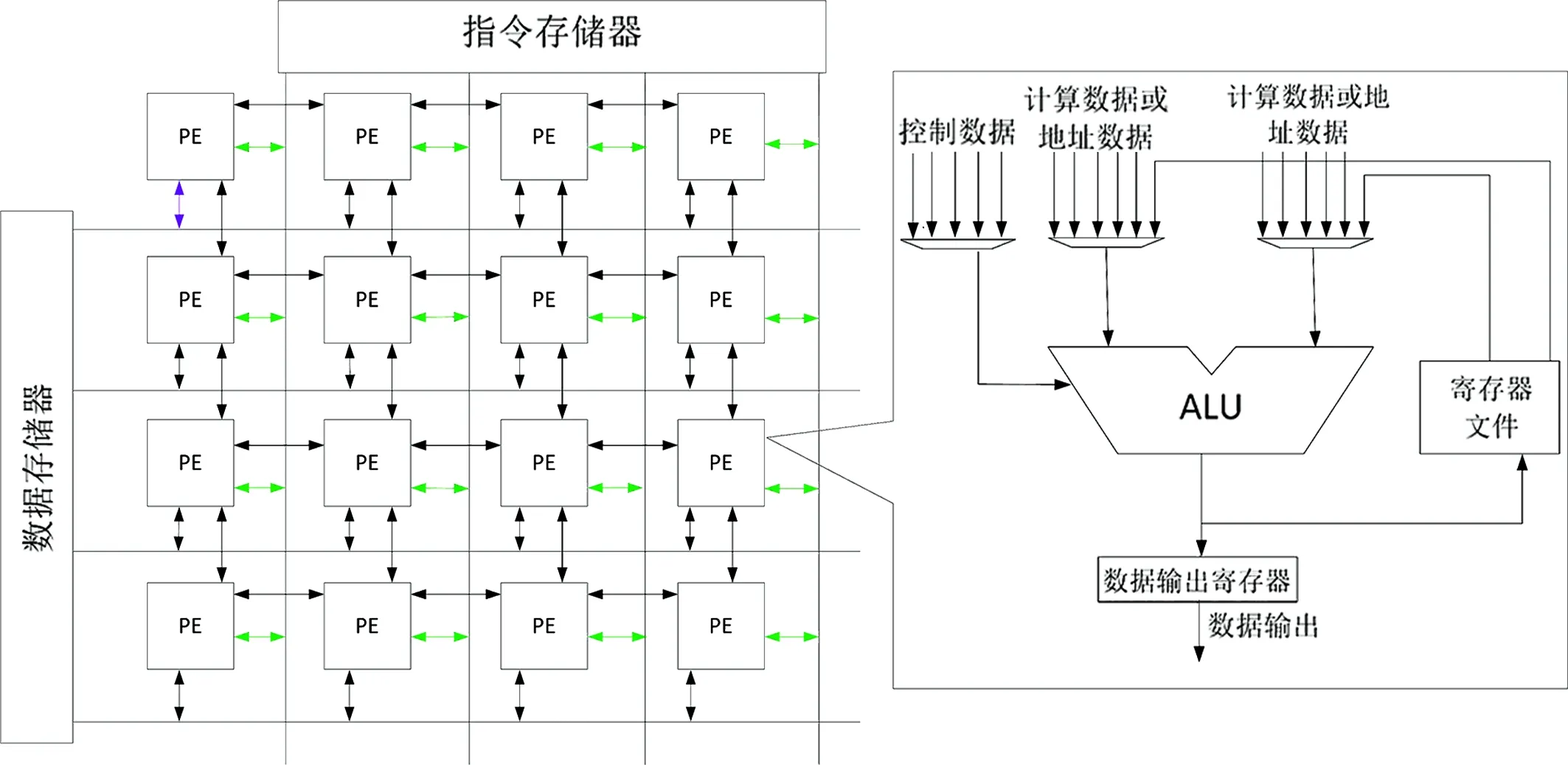
图1 网格型粗粒度可重构计算系统[1,5]Fig.1 Grid type coarse grained reconfigurable computing system[1,5]
这个架构是一种二维网格型可重构4*4架构,该体系结构由一块数据存储器模块(Date Memory )、一块指令存储模块和16块PE组成,这样的分布为了优化数据和指令在运算时执行的同步性.这三者的组成也是PEA(Process Element Array),每一个PE都相当于一个cpu可以进行独立的运算,边角的4个PE只可以和其相邻的2个PE相互连通,因此这4个PE是度维2的,边上出去度维2的PE剩下的8个PE度维3,而中间4个PE度维4.这是架构中PE的连接特点.其中每个PE内部都会有一个ALU (Arithmetic Logic Unit)其进一步展开可以完成加、减、乘、移位、多路选择等运算.本文正是针对其运算中的加和乘展开设计研究.
3 GCGRA乘法器和全加器设计与测试验证
3.1 乘法器设计与测试验证
对于乘法器已有的乘法思想进一步进行设计和测试验证.首先在要有一个乘法器设计思路,再进行代码程序设计进而生成原理图实现其乘法的功能,最后再对所设计的乘法器进行仿真波形验证,验证完成后对其进行综合执行得到性能参数,再对参数评估分析.
3.1.1 乘法器设计思路 乘法器设计思路下所述:
(1)初始乘法部分积为0,若被乘数和乘数的位数为4,则部分积初始化为00000000;
(2)对乘数的各位由高位到低位依次读取;
(3)若乘数读取时某位为1,则将部分积整体左移后加上被乘数;
(4)若乘数读取时某位为0,则将部分积整体左移;
(5)乘数最高位到最低位全部完成,形成最终的积.
3.1.2 乘法器原理图设计及生成 采用Verilog HDL作为设计语言,乘法器模块化互连原理图设计代码如下所述:
(1)module变量初始化:被乘数a、乘数b 、子积m,最终积mout,开始信号s_start、数据录入信号s_in、时钟clk、运算终止信号run_flag.
设定子积:对子积设定一位结束信号位赋值1,用于运算周期结束后触发运算终止信号run_flag,这里4*4 则m<=000010000,并对其他变量赋初始值:
always@( negedge s_start) //当s_start为0时将m清0,做计算前准备工作
begin
m <= 9'b0_0001_0000;//1作为结束标记
run_flag<=1; //运行标志,1为允许运行
a<=din; //将乘数放到寄存器
end
(3)设定运算规则:乘数最高位开始,若为1将子积左移后加被乘数,若为0只左移:always@( posedge clk)//每个时钟周期进行一次移位累加,位移累加运算
begin
if(run_flag==1) //只有运行运行时才执行下面操作
begin
if(b[3]==1)//从乘数的最高位开始判断
begin
m<=(m<<1)+a;//若为1子积先左移1位,再加被乘数
end
else
begin
m=m<<1; //若为0子积左移1位
end
b=b<<1; //找乘数的下一位
end
end
(4)运算左移子积次数触发运行标志:run_flag=m[9] 运算终止
(5)输出最终结果:assign mout=m[7:0]
(6)endmodule
由上6条代码生成的原理图如图2所述:

图2 4位*4位无符号乘法运算的原理图Fig.2 Schematic diagram of 4-bit * 4-bit unsigned multiplication operation
这个乘法器的组成是:1、2、5是D触发器,4、15、16是多位D触发器,其中4、15是带使能端的D触发器,3、7是左移寄存器,10是一位加法器,6、9、11、12、13、14是多路选择器.
3.1.3 乘法器测试波形验证
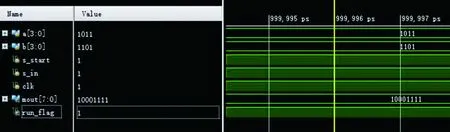
图3 4位*4位无符号乘法运算的测试波形Fig.3 Test waveform of 4-bit * 4-bit unsigned multiplication operation
a、b分别为4位的被乘数和乘数,s_start为运算开始信号,s_in为将乘数放入寄存器中的开始信号,clk为运算时钟,mout为最终的积,run_flag为计算终止信号.由测试波形可得:被乘数为1011,乘数为1101,最终积为10001111.运算结果是完全正确的,运算过程符合设计的思路.
3.2 全加器设计与测试验证
全加器的设计思想是由一位全加器不同的数量来构建自己所需要的全加器位数.来进一步优化设计用软件代码实现其电路图的生成,再进行仿真波形验证,确定设计没有错误后,对其综合执行得到性能参数来和乘法器的参数进行对比、评估.
3.2.1 全加器设计思路 全加器4位加4位无符号运算设计思路情况说明如下:
(1)一位全加器包括被加数、加数、低位进位、本位、进位;
(2)将四个一位全加器组合,用每个全加器中的被加数和加数位分表代表二个四位二进制数;
(3)低位全加器的进位作高位全加器的低位进位,最低位全加器的低位进位置0;
(4)每一位全加器的本文作为最终结果的本位,最后一位全加器的进位作为溢出位;
(5)4个全加器中4个本位作为最终结果低4位,最高位进位最为结果的第5位.

图4 4位+4位无符号全加器运算的原理图Fig.4 Schematic diagram of 4 bit +4 bit unsigned full adder operation
3.2.2 全加器代码设计及原理图生成 全加器4位加4位无符号运算的的代码设计与文献[12]类似,限于文章篇幅不在累述,生成的原理图如图4所述.
1由图可得4个1位全加器中的被加数和加数组分别合成一个4位的被加数和一个4位的加数.Add1是最低位,Add4是最高位.最低位的低位进位CIn默认为0,最高位的进位COut作为最终结果的最高位.低位的进位COut都与高一位的低位进位CIn相连接,而本位作为最终的结果依次排列.
3.2.3 全加器测试波形验证 my_a、my_b分别为4位的被加数和加数,my_cin为最低位的进位,始终默认为0.my_sum是最终和的前4位,my_cout是最高位的进位也是最终和的第5位,clk为运算时钟.由测试波形可得:被加数为0011,加数为0001,最终和为00100.运算结果是完全正确的,运算过程符合设计的思路.
3 乘法器和加法器分析与评估
对这些加法器进行测试、综合、执行.得到动态功耗、温度、LUT、IO等关键参数对比如下:Verilog HDL实验仿真采用软件仿真环境是Vivado2015,所用的仿真芯片是tbfg676-1,动态功耗部分精确到小数点后三位.表中提取了四个关关键参数:硅片上温度、动态功耗、使用LUT(look up tale)个数、IO口个数,进行分析评估.
3.1 结温分析
通过图表中数据得到的FPGA芯片结温(junction temperature)将其绘制成折线图的形式进一步评估:
由图1可得:全加器2位增加到4位、4位增加到8位、8位增加到16位、16位增加到32位温度分别提高了2.5℃、9.1℃、6℃、21.3℃.可见随着位数的增加FPGA芯片结温是递增的并且成近似指数形态增加,所以在设计全加器时要考虑数据位数的宽度.
乘法器的硅片上随着2位到32位的增加,硅片上温度总体呈增加趋势,但是幅度波动的比较小最低温度25.4℃,最高温度26.5℃.这是源于对乘法器改进的设计,使得乘法器的运行过程中只添加了运算的位数而运算时内部的结构变化不大.
3.2 动态功耗分析
由图5可得:加法器的动态功耗在2位到4位之间增加的1.315w和十六位的三十二位增加的11.228w,呈单调递增,近似于等比例函数.总体增长幅度在下降.说明随着位数的增加加法器的效能在提高.但是设计使用时要考虑到加法器温度、运算器、信号延迟的极限值不能盲目的提高位数增加效能.

图5 4位+4位无符号加法运算的测试波形Fig.5 Test waveform of 4-bit + 4-bit unsigned addition operation
而乘法器,二位增加到四位和十六位增加到三十二位所增加的功耗分别是0.017w和0.339增加的幅度整体呈指数增长.但是从数值上可以看到功耗改变的数值明显低于加法器.因为其内部的架构和计算原理不同于加法器这也是本乘法器设计的优点.
从图6和图7可得:随着位数的增加,加法器和乘法器所占用的LUT和IO口整体都是增加趋势.IO口个数上加法器呈现出高于乘法器的增长速度,而LUT的增长速度二者趋向于一致.这也是动态消耗中加法器的功耗呈现出高于乘法器的原因所在.后期再设计中需要针对这些参数加以改进才能更好的提高系统效能.
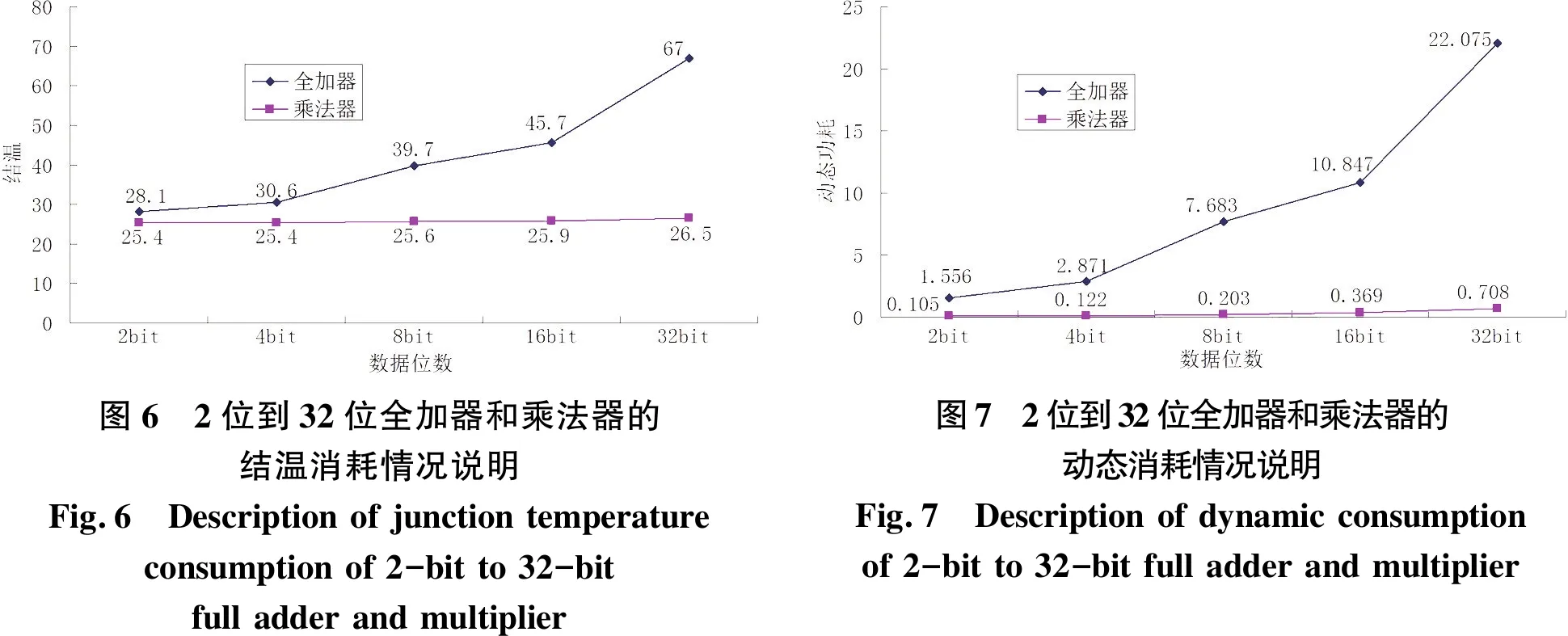
图6 2位到32位全加器和乘法器的结温消耗情况说明Fig.6 Description of junction temperature consumption of 2-bit to 32-bit full adder and multiplier图7 2位到32位全加器和乘法器的动态消耗情况说明Fig.7 Description of dynamic consumption of 2-bit to 32-bit full adder and multiplier
3.3 SliceLUT个数分析
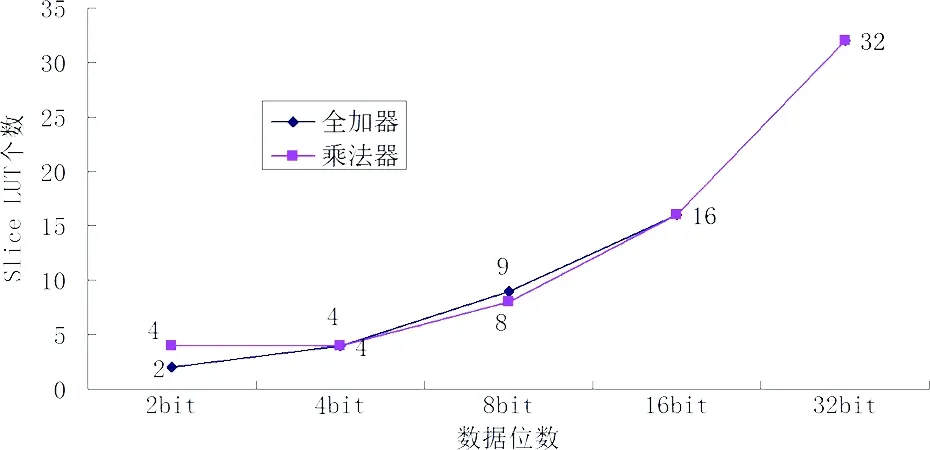
图8 4位全加器与4位乘法器需 要Slice LUT个数的比较Fig.8 4 bit full adder and 4 bit multiplier need to compare the number of Slice luts
由图8可得:全加器在2位时所使用的LUT要比乘法器多2个.但是随着位数的增加二者使用情况趋于一致.没有较大的波动,因此在这个参数的使用情况上分析在2位到4位时乘法器对LUT的使用要略高于全加器,而在4位到16位时全加器使用LUT的个数要略高于乘法器,16位到32位时使用情况基本一致.
从数据的整体情况上来看全加器和乘法器对LUT的使用情况在4位和16位时分别有二个节点,前后对有一定的影响.但是总体上来看二者的使用情况大体一致.因此这项参数在两种运算器中的影响要小于其他参数,在以后的组合设计中可以略微考虑到二者LUT的使用情况.
3.4 I/O个数分析

图9 4位全加器与4位乘法器需要 I/O个数的比较Fig.9 4 bit full adder and 4 bit multiplier need I/O number comparison
由图9可得:从2位增加到4位、4位增加到8位的过程中乘法器的I/O增长个数为2、16而全加器的增长个数为6、18.但是8位增加到16位、16位增加到32位的过程中乘法器的I/O增长个数为32、64而全加器的增长个数为18、48.
I/O个数增加意味着功耗的增加,由此可以发现乘法器提高到8位之前效能是要高于全加器的,而在8位之后乘法器随着位数的增加依然是2倍式的增加,全加器明显低于乘法器的增长,也就是在8位以后全加器的效能要高于全加器,我们在后期设计组合中可以考虑到二者的效能最高点进行组合运算的设计,所以说将能耗参的研究意义重大.
4 结束语
本文对二维网格型粗粒度可重构计算系统的架构简单的介绍,对其中ALU展开的全加器、乘法器深入设计并进行仿真波形测试,并综合执行后对得到的动态功耗、结温、查找表、IO个数进一步比较数据得出功耗规律,为提高运算单元的效率提供重要参考.但是本文在系统部件的仿真设计上还有进一步完整设计和组合设计的完善空间.
