高频刺激对异质性前馈神经网络信号传导的影响

薛 彬，秦迎梅，刘 靖

（1.天津职业技术师范大学自动化与电气工程学院，天津 300222；2.天津职业技术师范大学天津市信息传感与智能控制重点实验室，天津 300222）

人类的大脑是自然界中最复杂的信息处理系统之一，也是调控人体各项机能的中枢，其内部是由约1 000 多亿个神经元通过突触进行相互连接的高度复杂的神经元网络[1]。在生物神经科学的研究中，神经系统能够对外部刺激信息进行处理，完成信息的编码与解码，实现信息在神经网络中的传播，从而调控机体的各项功能。越来越多研究发现，一些神经精神疾病（如帕金森、阿尔兹海默、癫痫等）的发生与大脑结构和功能网络密切相关，如癫痫疾病患者发病期间的脑功能网络与未发病时的网络特性存在显著的差异，并且癫痫疾病下神经元的放电模式也与正常网络下的放电有所不同。所以，研究不同拓扑结构下的神经元网络的动力学特性具有重要意义。在文献[2]中，作者研究了拓扑结构对前馈网络中信号传导的影响，结果表明，不同前馈网络拓扑结构对神经元信号传导的影响不同。在文献[3]中，作者对噪声作用下的前馈网络中不同拓扑结构对信号传导的影响作了相关研究，研究结果表明，不同强度的噪声对不同拓扑结构网络中信号传导的影响不同，但对高频刺激作用下的前馈神经网络中不同拓扑结构对信号传导的影响尚未研究。在以往的大部分研究中[4-6]，构建神经网络时所考虑神经网络中的神经元为同质的，然而在现实的生物神经网络中，神经元并非完全相同，而是存在着差异性。因此，研究神经元异质性参数对信号传导的影响，旨在为揭示神经疾病的发作机理提供重要的途径。本文构建3 种异质性拓扑结构的前馈神经网络，研究其在高频刺激作用下异质性拓扑结构对信号传导的影响。

1 神经元网络模型

1.1 FitzHugh-Nagumo（FHN）神经元模型

研究采用异质的FHN 神经元模型来构建网络模型。FHN 神经元模型是由FitzHugh R 和Nagumo J 提出的一个理想化模型，是在HH 模型某些条件下简化得到的二维模型，它被广泛应用于研究神经元初次放电活动。FHN 模型虽简洁，却具有基本的神经元特性，如阈值性和不应期特性[7]。除此之外，FHN 神经元模型能够很好地描述兴奋性神经元的膜电位对外部刺激的响应，同时还能够反映对神经元放电活动的主要特征。由FHN 神经元构建的网络在外部扰动的作用下，动作电位以及神经元放电模式在神经纤维上的传播情况能够被很好地描述出来。FHN 神经元模型的表达式为

式中：i 为神经网络的第i 层，i=1，2，3，…，N；j 为第i层中的第j 个神经元，j=1，2，3，…，N（N=200）；xi，j、yi，j分别为膜电位和恢复变量；为流入第i 层的第j 个神经元总电流之和。

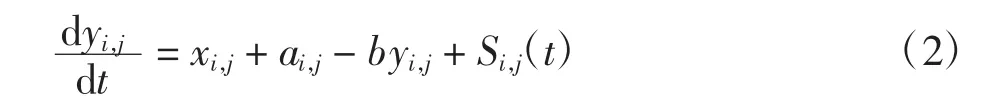
式中：Si，j（t）为外部刺激；ai，j为神经元的兴奋状态。

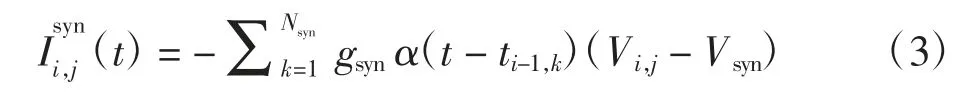
式中：Nsyn为神经网络中前一层（（i-1）层）神经元与第i 层中的第j 个神经元连接的总数之和；gsyn为连接强度；τ 为突触时间常数，一般情况，τ 设置为0.2 ms。

神经元突触的类型受逆转电位影响，分为兴奋性神经元与抑制性神经元，式（3）中的Vsyn值为0 时代表该神经元为兴奋性神经元，当Vsyn值为-2 时为抑制性神经元，神经元突触的类型将会直接影响到神经元的突触后膜的接收电流[8]。对于一个没有输入的单个FHN 神经元模型来说，Andronov-Hopf 分叉现象发生在a=0.7 时。当a ＞0.7 时，神经元处于兴奋状态，因此在同质神经网络中设置a=ai，j=0.7（b=0.45，ε=0.08）[9]。

1.2 异质性前馈神经网络模型

多层前馈神经网络是目前研究较为广泛的一种网络形式，它具有层次化的拓扑结构，其每一层网络结构相当于模块化的神经元集群。前馈神经网络能够很好地模拟网络中神经编码的传输特性，通常被用来研究感觉器官的神经编码，神经元的刺激信息能够从一层传递到下一层[10]。研究中采用异质性的FHN 神经元来构建前馈神经网络模型，网络中每层由200 个FHN 神经元构成，层内神经元之间没有耦合，但相邻的层与层之间通过连接概率P 进行耦合。

在该神经网络模型中，向前馈神经网络引入异质性参数，此时FHN 神经元模型参数ai，j不再为常数0.7，忽略模型中其他因素的影响，根据不同的兴奋性来描述神经元异质性，ai，j均匀分布在[a-Ha，a+Ha]之间，其中Ha决定神经元的异质性水平[11]，a-Ha≥0.7以确保所有神经元都处于亚阈值状态。在研究中，考虑了3 种不同度分布的前馈神经网络模型中异质性参数对信号传播的影响，3 种度分布分别为相同分布、均匀分布和指数分布。对于相同分布来说，其每个神经元接收来自上一层神经突触的连接总数符合Nsyn=N×P（N=200，P=0.1），因此对于相同分布的结构中的神经元接收来自上层突触连接的最小值为0，最大值为20。而均匀分布和指数分布的神经元突触连接总数分别满足在区间[0.2×N×P]（N=200，P=0.1）中和满足函数f（x）=λe-λx，其中E（x）=1/λ，λ=1/（P×N）[12]。

2 高频扰动下的异质性前馈神经网络放电特性

在生物神经系统中，神经元在接收与处理信息的过程中总是不可避免地受到噪声或者高频周期信号的影响。噪声主要来源系统内部参数的升降以及内部环境的变化。它对神经系统的实际功能有着密切的联系。研究表明，噪声对于一些重要的动力学过程的发生起到了积极作用，这种积极的影响主要表现在随机共振的出现[13]。此外，还有研究表明，双稳态系统中的噪声的积极作用可以被其他信号代替，如高频周期信号。在双稳态系统中，高频信号能够促进低频信号在神经网络中传导的现象称为振动共振[14]。频率与振幅作为高频刺激的主要特征参数，在大脑神经元活动的调节中起着重要的作用。在一个正常的神经网络中，高频周期的幅值和相位并不是完全相同的。所以在研究神经网络信号的传导时，考虑不同幅值与相位作用的高频刺激十分必要。

研究构建了一个幅值和相角同时变化的高频扰动作用下的前馈神经网络，向网络第1 层分别引入高频和低频刺激，即Si，j（t）=ALsin（2πt/ Ts）+Ai，jsin（2πt/TH+φi，j），其他网络层只引入高频信号Si，j（t）=Ai，jsin（2πt/TH+φi，j）（i ＞1），低频信号Ts=30，低频幅值AL=0.05，高频信号TH=1.7 ms，低频信号的周期要远远大于高频信号周期[15]。Ai，j代表每层每个神经元接受的高频信号的不同幅值，其均匀地分布在区间[AH（1-HA），AH（1+HA）]；HA代表幅值变化范围区间的水平因子；AH代表高频刺激的平均幅值[16]。此外，高频刺激的相位满足φi，j=j2π/N。

为了更好地理解信号在层间的传播机制，研究中选择了2 种不同的高频平均幅值AH进行比较，AH分别为0.09 和0.11，这里固定幅值变化范围区间水平因子参数HA为0.4，结果如图1 所示。图1（a）、图1（b）分别描述了高频平均幅值适中与过高时，神经元放电序列的变化。研究发现，当高频平均幅值适中时，高频信号能够很好地促进低频信号传导，而当高频平均幅值过大时，低频信号的信息随着信号的传播开始失真。所以，选择适当的高频平均幅值信号至关重要。

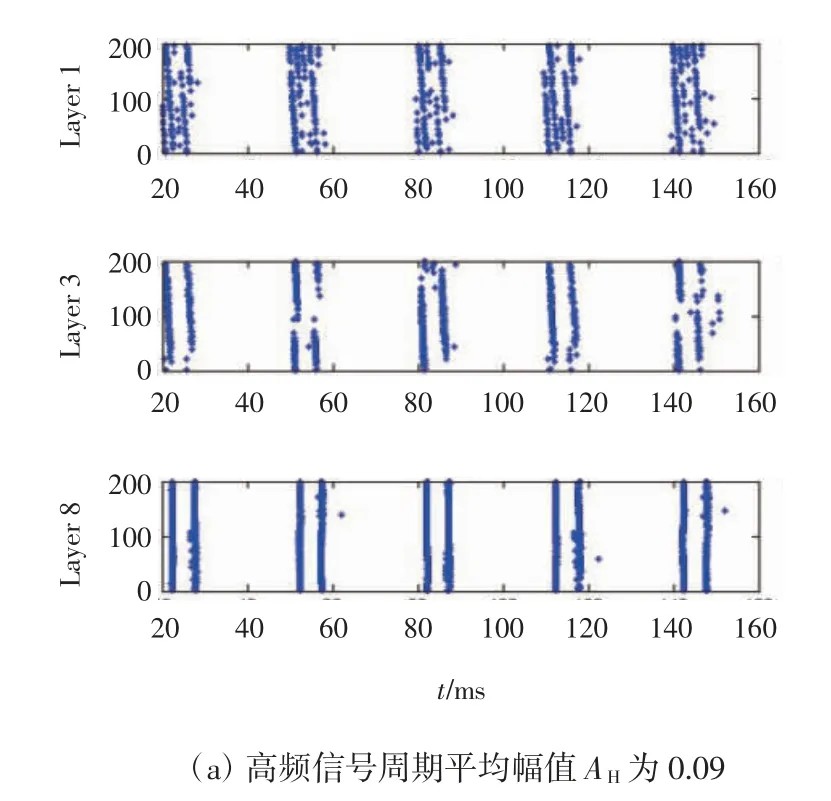
图1 前馈神经网络中信号的尖峰放电序列

3 高频刺激对异质性前馈神经网络信号传导的影响

为了解信号传播特性与异质性前馈神经网络之间的关系，分别研究了神经元在外部刺激作用下，在3种不同拓扑结构（度分布）前馈神经网络中神经元的放电率F 以及在相同分布结构作用下的空间相干性K，构建了同质性前馈网络与不同程度异质性的前馈神经网络，并对放电率进行对比，观察异质性对信号传播的影响。这3 种拓扑结构分别为相同分布、均匀分布、指数分布。层之间的连接概率与连接强度是神经网络的重要参数，本研究将3 种网络拓扑结构设置为相同连接强度和连接概率，分别为0.04 和0.1。

3.1 高频刺激对异质性前馈神经网络放电率的影响

分别向3 种度分布结构的异质性前馈神经网络中引入不同幅值的高频刺激，观察神经元的放电情况。异质性系数为Ha=0、0.02、0.05 时，不同度分布的异质性前馈神经网络的放电率分别如图2、图3和图4 所示。3 种分布结构中，高频刺激在适当幅值作用下都能够对低频信号起到促进作用。其中，为确保所有神经元都处于亚阈值状态，a-Ha≥0.7，即0 ＜Ha≤0.05。本文分别取Ha为0、0.02 以及0.05 进行研究。图2 中的神经元异质性系数为0 时，即前馈神经网络为同质的3 种拓扑结构中，均匀分布与指数分布随着高频平均幅值的增强而增强的趋势要大于相同分布，而且3 种分布下的异质性高频刺激平均幅值过低时，并不能够对信号起到促进作用。图3 的3 种神经网络中，与同质神经网络相比，异质性使得神经元的放电率变得更强，并且促进了信号在高频刺激下的传导。

图2 异质性系数Ha=0 时，不同度分布的异质性前馈神经网络的放电率

图3 异质性系数Ha=0.02 时，不同度分布的异质性前馈神经网络的放电率

图4 为神经元异质性系数提高至0.05 时3 种拓扑结构网络的放电率。从图4 可以看出，3 种拓扑结构中低平均幅值的高频刺激作用下的放电率也被提高了。这表明，与同质前馈神经网络相比，高频刺激作用下的异质性前馈神经网络的放电率随着异质性系数的增强而增强。此外，在3 种不同拓扑结构网络中，当异质性系数相同时，对比3 种不同网络发现，服从指数分布的前馈神经网络比相同和均匀分布的前馈神经网络的放电率更强，且服从均匀分布与指数分布的前馈神经网络比相同分布的前馈神经网络对异质性的作用更敏感。

3.2 高频刺激对异质性前馈神经网络空间相干性的影响

为进一步了解高频刺激对异质性前馈神经网络信号传导的影响，分别研究了高频刺激对相同度分布异质性前馈神经网络下空间相干性的影响。空间相干性表示网络各层放电同步性的优劣程度，当空间相干性较大时，表明网络各层放电同步性较好；当空间相干性较小时，表明网络各层放电同步性较差。前馈神经网络的空间相干性用平均相关参数K 表示，K 是根据神经元在某一层的激活时间计算得到的。K 的函数表达式为

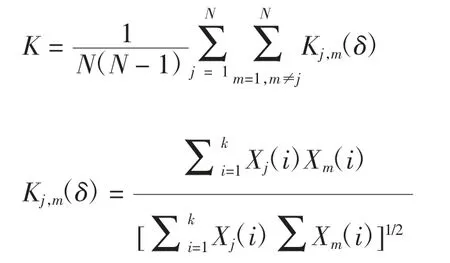
将X 中的每个元素设置为1 或0，如果第i 个点有一个序列X，那么X（i）=1，否则X（i）=1。用K 值估计同步状态，如果K 值接近1，则该层更有可能处于同步状态。相反，如果K 值接近0，则该层更有可能处于非同步状态。相同分布的前馈神经网络中神经元的空间相干系数K 的热力图如图5 所示。

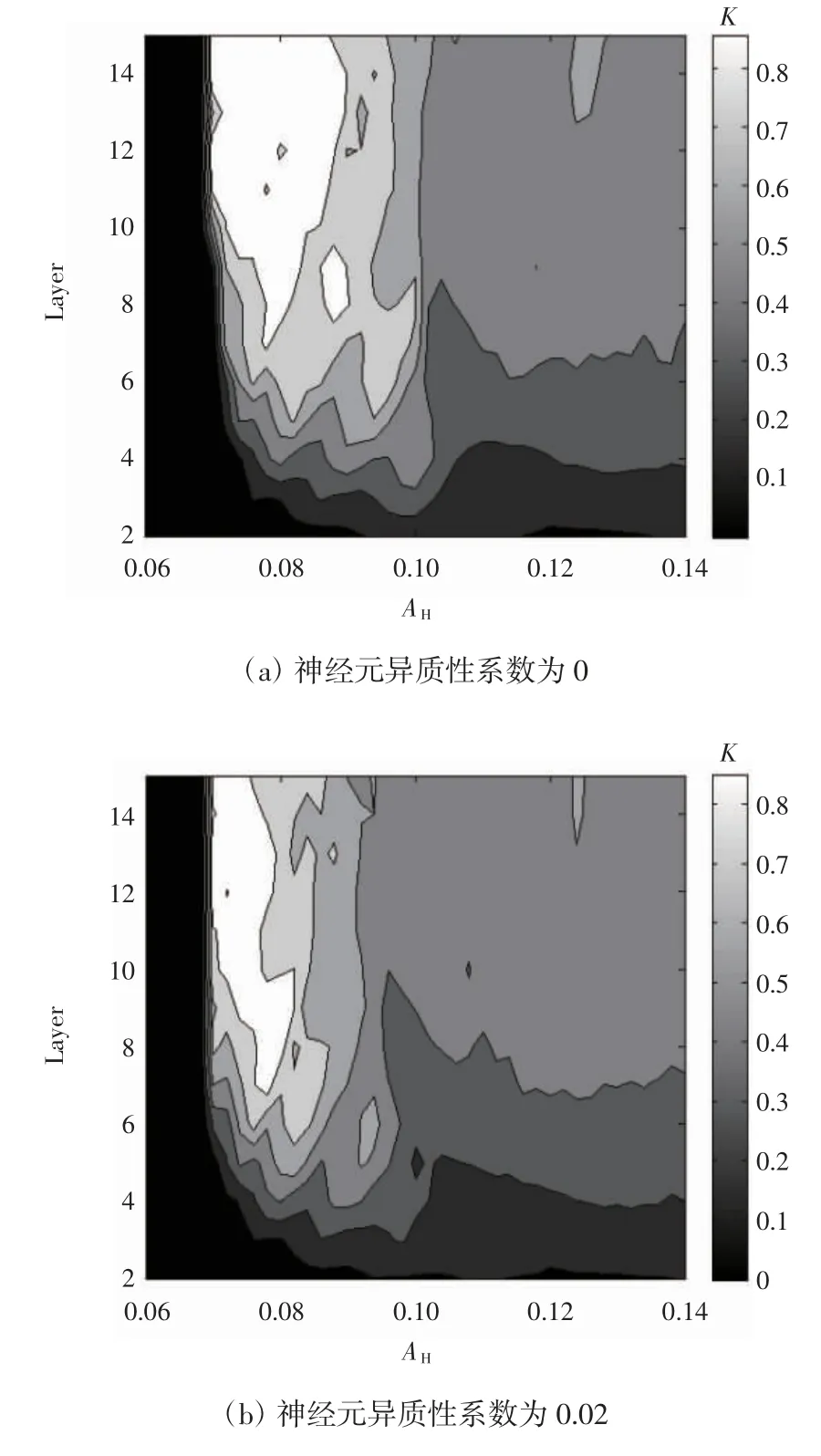
图5 相同分布前馈神经网络中神经元空间相干系数K 的热力图

从图5 可以明显看到，随着异质性系数的增大，空间相干性系数K 最大值的区域逐渐变小。当异质性系数达到0.05 时，K 的最大值在0.4 左右。当神经网络为同质性时，如图5（a）所示，空间相干性系数K 最大值分布在AH范围的[0.75，0.85]，在该区间范围内，空间相干性系数K 随着层数的增加而变大，即神经元在层之间的传播逐渐趋于同步。随着异质性系数增大，空间相干性系数K 最大值分布区域范围开始变化，且最大值也越来越小。总之，在高频刺激作用下，空间相干性受神经网络异质性参数与高频幅值参数共同作用的影响。

4 结语

本文采用非线性动力学方法，研究了在高频刺激作用下，神经元异质性对相同分布、均匀分布和指数分布的3 种不同拓扑结构前馈神经网络放电率和空间相干性的影响。研究结果表明：适中的异质性参数能够促进高频刺激下信号在前馈神经网络中的传导。在生物神经网络中，神经元动力学参数的改变会对大脑的功能造成不同程度的影响，异质性前馈神经网络被认为有可能是引发癫痫类病态振荡活动发生质变的因素。因此，研究高频刺激作用下的异质性前馈神经网络中不同拓扑结构对信号传导的影响具有重要意义。