时速140 km地铁中等减振轨道钢轨振动特征分析

杨麒陆

(1.中国铁建昆仑投资集团有限公司 四川成都 610031；2.中铁建昆仑地铁投资建设管理有限公司 四川成都 610031)

1 引言

随着我国国民经济快速发展，城市化进程也随之加快，各大城市纷纷规划新经济区以缓解中心城区人口及产业聚集压力，而连通市中心城区与新经济区的高速地铁线路如雨后春笋，方兴未艾[1－2]。

各大城市在建或规划中的连通中心城区与新经济区的城市轨道交通线路大多提高了设计时速，如广州地铁3号线最高设计时速达到了120 km，是我国第一条时速120 km地铁线路，此外东莞地铁2号线、上海地铁9号线、深圳地铁11号线等地铁线路最高设计时速也纷纷达到120 km，而时速更高的140 km城市轨道交通线路如成都地铁18号线也即将投入试运行[3]。

列车设计时速的提高在带动经济发展、方便人民出行的同时也给轨道养护维修、行车安全、环境噪声控制等方面带来了更多不确定因素，而带来这一系列不确定因素的关键原因之一就是高速运行状态下车辆与轨道的耦合振动更加复杂[4－6]。

对钢轨振动频率、振动加速度幅值等钢轨振动特征的分析有助于研究钢轨不均匀磨耗、扣件弹条折断、减振降噪等问题。周昌盛等通过对某最高设计时速120 km地铁的跟踪研究发现弹条折断现象主要发生于时速80 km以上区段，钢轨短波波磨引起的钢轨振动主频漂移接近弹条固有频率是引起弹条折断的重要原因；THOMPSON D J的研究表明钢轨是1 600 Hz以下轮轨接触噪声的主要声源之一[7]；韦凯对钢轨扣件胶垫进行了激振频率变化的动测实验，结果表明忽略扣件胶垫的频变特性会低估钢轨的振动情况[8]，而扣件胶垫激振频率与列车行车速度息息相关。可见随着地铁列车时速的提高，钢轨的振动特征将发生显著变化。

目前国内对时速140 km地铁轮轨耦合振动的研究还鲜有报道。为探究时速140 km地铁钢轨的振动特征，本文以某城市在建的时速140 km地铁为研究对象，利用翟婉明院士新型显式积分法(翟方法)进行车辆－轨道耦合模型建模；为准确研究钢轨200 Hz～1 600 Hz的中高频振动特征，钢轨模型选用可考虑剪切变形的Timoshenko梁模型代替传统Euler梁模型建模，着重研究时速140 km地铁中等减振轨道钢轨加速度幅值、振动加速度振级、钢轨振动主频等指标，为今后时速140 km地铁研究提供参考。

2 基于翟方法的车辆-轨道耦合模型构建

(1)地铁A型车建模

对地铁A型车进行全车力学建模。车体与转向架由二系悬挂相连，转向架与轮轴通过一系悬挂连接，一个转向架下的一系悬挂包含四组钢弹簧与液压阻尼器。该模型为十自由度客车模型[9]，能准确模拟列车运行过程中车体(Mc)的沉浮运动(Zc)、点头运动(βc)、前后转向架(Mt)的沉浮运动(Zg)和点头运动(βg)，以及4个轮对(Mw)的垂向运动(Zwj，j＝1～4)。列车模型使用的主要垂向计算参数见表1。

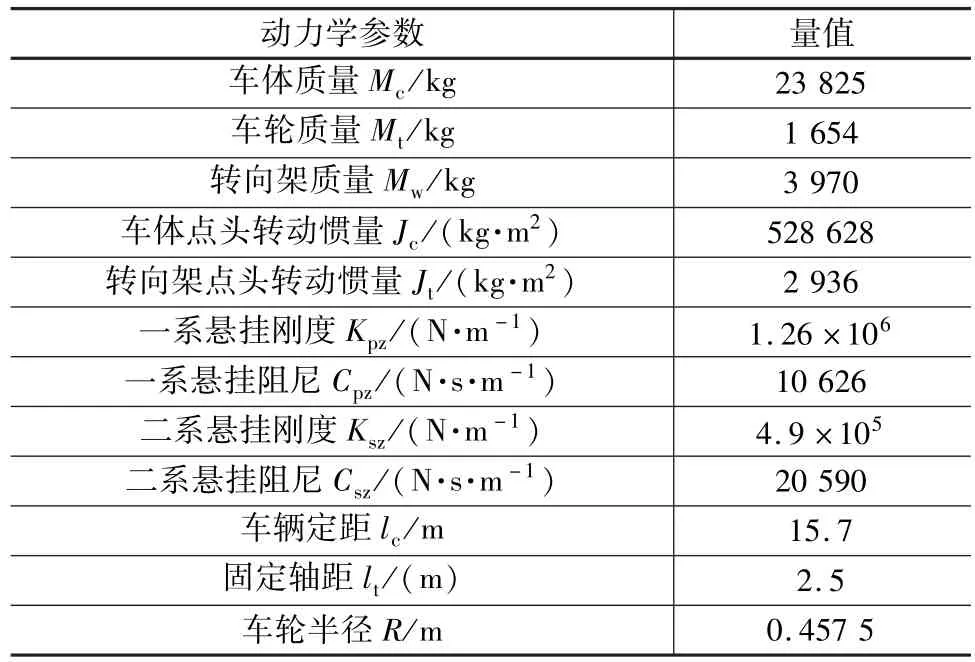
表1 地铁A型车垂向模型计算参数

列车全车垂向车辆－轨道耦合示意图见图1。

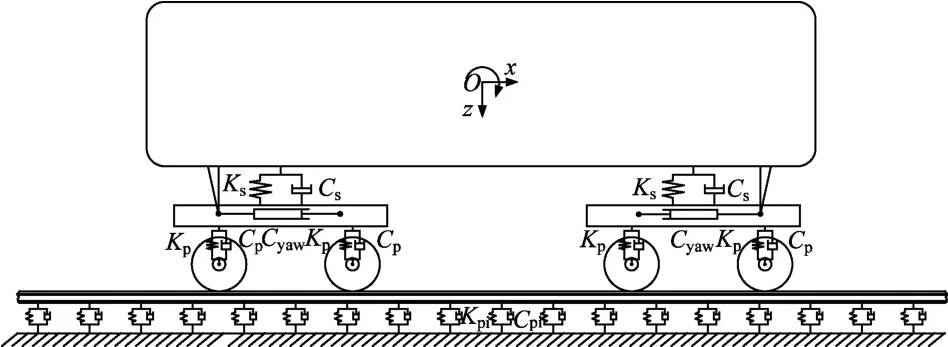
图1 列车全车垂向车辆-轨道耦合示意

车辆－轨道耦合模型列车编组采用两节编组而非实际行车的八节编组，这样既考虑了相邻列车转向架对钢轨垂向位移的影响，也兼顾了计算效率。

(2)基于Timoshenko梁的轨道子结构模型

在车轨耦合新型显式积分计算法中，钢轨通常采用梁单元模拟。经典梁体理论模型主要有Euler-Bernoulli梁体理论、Rayleigh梁体理论、Shear梁体理论、Timoshenko梁体理论四种。Euler-Bernoulli梁体理论，即工程梁理论，最早出现并在较为广泛的工程实践中广获认可。该模型简单实用，常用于细长梁的模拟，因此也广泛应用于钢轨振动的模拟。但是该模型基于平截面假定，未能够把剪切与扭转变形加以考虑，会高估高阶振型的频率。Rayleigh梁体理论在Euler-Bernoulli梁理论上加入梁横截面的扭转变形因素，略微降低了Euler-Bernoulli梁对高频振动分析的误差。Shear梁体理论是在Euler-Bernoulli梁的分析基础上又加入了对梁横截面剪切变形的分析，大为消减Euler-Bernoulli梁对高频振动的高估，但较实测结果而言Shear梁模型还是过高地估计了梁模型的高频振动。Timoshenko梁体理论是在Euler-Bernoulli梁模型的基础上既考虑梁横截面扭转变形，又考虑梁横截面的剪切变形的影响，较前三者能更加准确地分析细长梁的高频振动[10－12]。

随着地铁运行时速的提高，加之运行过程中钢轨短波磨耗的加剧，钢轨的高频振动也愈发不可忽视。我国地铁正线多采用中国60轨，本文钢轨建模采用能考虑横截面剪切及扭转变形的Timoshenko梁模型。钢轨具体参数见表2。

表2 轨道模型的计算参数

基于新型显式积分法的车轨耦合模型，钢轨部分采用模态叠加法描述其振动情况。基于Timoshenko梁模型的钢轨垂向振型微分方程:

钢轨扭转振型微分方程:

式(1)、式(2)中qk(t)为钢轨正则振型函数；NM为钢轨所截取的模态阶数；ωk(t)为扭转振型函数；Ar为钢轨横截面积；Gr为钢轨剪切模量。

中等减振扣件安装于长枕埋入式整体道床中，扣件系统下部基础质量较大，且相对于钢轨而言几乎没有弹性，故将下部基础视作为刚性基础。

(3)基于Timoshenko梁的车辆－轨道耦合模型

翟方法是在Newmark-β隐式积分法的基础上通过对称性构造而来，其基本原理是根据前两个积分步骤的位移、速度、加速度来预测下一步的位移及速度，在此基础上利用系统运动方程预测下一步的加速度，如此开启循环求解[7]135－142。新型显式积分法表达式:

式中，n为某一积分时刻；n＋1为下一积分时刻；n－1为上一积分时刻；{X}n为广义位移矩阵；{V}n为广义速度矩阵；{A}n为广义加速度矩阵；Δt为积分步长；ψ和φ为控制方程独立性参量(启动积分时令ψ＝φ＝0)。

列车车轮与轨道的接触部位建模是车轨耦合动力学的关键所在，本文所建立的车辆－轨道耦合模型中，列车车轮与轨道的接触关系模拟是基于Hertz非线性弹性接触理论，见式(4)。

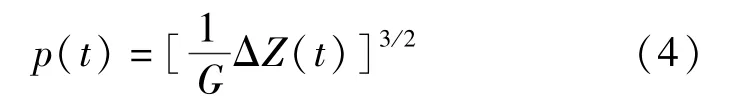
式中，G为列车车轮与钢轨的接触常数(m/N2/3)；ΔZ(t)为列车车轮与钢轨间相对的压缩量(m)。

锥形踏面接触参数取值为:

G＝4.57R－0.149×10－8

磨耗型踏面接触参数取值为:

G＝3.86R－0.115×10－8

式中，R为车轮半径，取值见表1。

列车车轮与钢轨间弹性压缩量ΔZ(t)由静压缩量ΔZj0(t)和相对位移ΔZjwr(t)两部分组成，即:

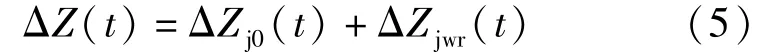
列车车轮与钢轨间静压缩量及轮轨相对位移:

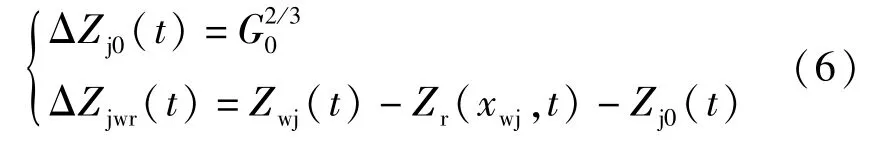
式中，Zwj(t)为t时刻车轮j的位移；Zr(xwj，t)为t时刻车轮j下的钢轨位移；Zj0(t)为车轮j下的轨道不平顺值。

当列车车轮与钢轨间相对位移ΔZjwr(t)小于0时，表明车轮已脱轨，此时轮轨力p(t)＝0。因此轮轨接触力的表达式为:

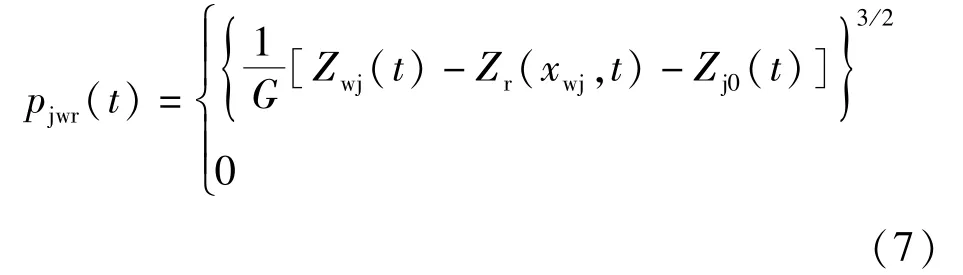
(4)轨道不平顺

相关研究表明，我国地铁轨道不平顺功率密度谱特征与美国六级谱较为接近[9]99－104，但由于美国六级谱最短波长为1.524 m，无法考虑短波不平顺对轨道高频振动的影响，故叠加我国实测波长0.01～1 m的短波不平顺谱[10]，得到波长范围0.01～200 m的轨道不平顺值，见图2。

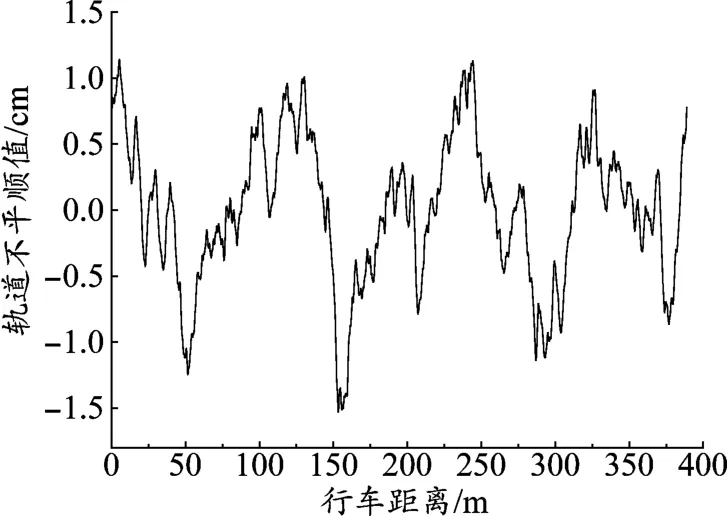
图2 叠加短波不平顺的美国六级谱

3 基于Timoshenko梁模型的地铁轨道振动情况仿真模拟

由于本文重点研究对象为时速140 km地铁钢轨的振动特征，故取时速140 km两节编组列车通过轨道既定位置作为实验组进行模拟，再分别取时速120 km、80 km两节编组列车作为对照组进行对比分析。仿真分析时假设地铁A型车均为满载状态，载客量310人，乘客质量按61 kg计算[13]。

3.1 轨道时域振动情况仿真模拟

对速度140 km/h、120 km/h、80 km/h 下列车通过既定测点时钢轨的垂向振动加速度进行仿真模拟，见图3。

图3 不同时速下钢轨加速度对比曲线

从图3可看出，随着地铁列车运行速度的提高，钢轨加速度幅值也随之递增，钢轨加速度峰值出现在第二节车的第一轮对通过时。时速140 km地铁列车通过时钢轨加速度峰值为624.2 m/s2，较时速120 km地铁钢轨加速度峰值增加约58.3%，较时速80 km地铁钢轨加速度峰值增加约100.6%。可见速度增加对钢轨加速度的影响很明显。

对速度140 km/h、120 km/h、80 km/h 下列车通过既定测点时钢轨的垂向位移进行仿真模拟，见图4。

由图4可看出，随着地铁列车运行速度的提高，钢轨垂向位移变化不明显，列车速度增加对钢轨垂向位移的影响较小，这也与某时速120 km地铁现场钢轨位移动测试验结论相吻合[5]。

图4 不同时速下钢轨垂向位移对比曲线

3.2 轨道频域振动情况仿真模拟

对140 km/h、120 km/h、80 km/h 速度下钢轨加速度进行三分之一倍频变换得到频域内钢轨加速度三分之一倍频的中心频率，见图5。

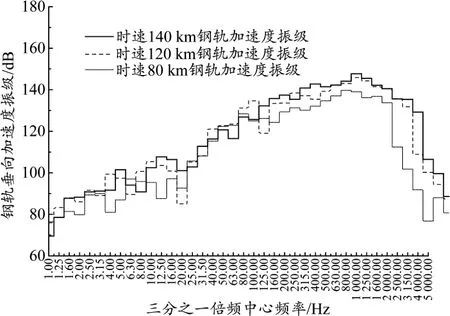
图5 钢轨加速度振级对比曲线

由图5可知，列车运行速度对钢轨加速度主频影响较大，随着列车运行速度的提高，钢轨加速度主频也随之增高。时速140 km地铁钢轨加速度主频为1 000 Hz，较时速80 km地铁钢轨振动主频向高频方向漂移明显，且低频振级也明显高于时速80 km地铁。时速140 km地铁钢轨垂向振动主频对应的垂向振动加速度振级为147.7 dB，较时速120 km、80 km地铁增幅分别为1.3%、5.7%，增幅并不及钢轨加速度幅值增幅明显。

建议在时速140 km地铁设计及运营时，充分考虑钢轨垂向振动主频，尽量避免选取前三阶固有频率与钢轨振动主频重合的扣件系统，或是通过调节扣件刚度、弹条插入位置等措施避开钢轨振动主频。

4 结束语

(1)时速140 km钢轨加速度主频明显高于时速80 km地铁，且主频处钢轨加速度振级也有所提高，建议尽量不要选取前三阶固有频率与钢轨振动主频重合的扣件系统，或是通过调节扣件刚度、弹条插入位置等措施使扣件前三阶固有频率避开钢轨振动主频。

(2)时速140 km地铁钢轨加速度幅值较120 km、80 km地铁增幅较为明显，地铁运营过程中建议定期打磨钢轨以控制短波磨耗。

(3)时速140 km地铁钢轨垂向位移较时速120 km、时速80 km地铁增幅不大，无需过分考虑钢轨位移带来的形变对轨道结构的影响。