同时震源数据的直接反演分离

王坤喜 毛伟建 张庆臣 李武群 詹 毅 孙郧松

(①中国科学院测量与地球物理研究所计算与勘探地球物理研究中心，湖北武汉 430077； ②大地测量与地球动力学国家重点实验室，湖北武汉 430077； ③中国科学院大学，北京 100049； ④东方地球物理公司物探技术研究中心，河北涿州 072751)

0 引言

地震数据采集需要考虑成本与质量之间的平衡。传统的地震勘探野外数据采集过程中，相邻炮的激发时间间隔较大，采集效率低，成本高。同时震源(simultaneous source)采集技术，也称多震源地震数据采集技术，改变了传统的采集方式。当震源数量一定时，同时震源采集能够缩短采集时间，增大覆盖范围；通过增加震源数量，提高覆盖次数，改善对地下构造的照明质量[1-3]。

同时震源数据采集能够提高采集效率和改善照明质量，但是相邻震源之间会产生“串扰噪声”，因此同时震源数据不适用于传统的处理流程。目前此类数据的处理方法主要有两大类： ①直接成像，即直接用同时震源数据进行偏移成像，这类方法受到串扰噪声的干扰，成像质量会降低[4-10]； ②分离法，即先对混合数据进行分离，得到类似单个震源激发的数据，再用常规地震方法进行处理。

分离法进一步划分为滤波类和反演类。从共炮域变换到其他域，在伪分离记录中主震源信号是连续的，混合噪声不再具有连续相干性。据此，Moore等[11]和Akerberg等[12]在共偏移距域进行滤波； Huo等[13]利用多方向矢量中值滤波法对地层倾角进行扫描，求得最佳倾角后，再利用中值滤波去除共中心点域的混合噪声。Yang等[14]提出先利用PWD(plane-wave destruction)求取地层的倾角信息，再结合矢量中值滤波对串扰噪声进行压制。反演类方法的思路是施加约束条件，将分离问题变为反演问题。Doulgeris等[15]设计了迭代算子，在共检波点域压制噪声； Mahdad等[16]在频率—波数域分选伪分离数据，设计迭代算法，分离混合波场；韩立国等[17]结合多级中值滤波和Curvelet阈值迭代去噪算法，实现了混合数据的分离； Chen等[18]、祖绍环等[19]、Xue等[20]和宋家文等[21]分别将地震数据转换到Seislet域、Curvelet域、Radon域和频率—波数—波数域(FKK)，然后在稀疏域对混合地震数据进行正则化稀疏约束迭代，实现了混合数据的分离； Zu等[22]引入两个卷积算子构造逆问题，先求得地震信号的倾角，然后通过共轭梯度算法求解该逆问题，实现混叠数据的分离； Zhou等[23]在共检波点域利用秩缩减滤波器和相干滤波器，通过迭代压制非相干信号，也取得了不错的效果。

以上分离方法都要施加约束条件，比如地震信号的相干性和稀疏性。Wapenaar等[24-26]在地震多维反褶积干涉的基础上，对同时震源数据的分离进行了研究，认为可以不施加这些额外的约束条件。在时间延迟算子的伪逆中，增加了基础点扩散矩阵，在满足一定的分离条件下，将混合数据按延迟时间进行归位，直接得到分离结果。

本文通过推广基础点扩散矩阵，将检波点和炮点规则排列采集的同时震源数据分离方法拓展应用于不规则排列采集的同时震源数据分离。

1 方法原理

1.1 数据混合的编码方式

(1)

(2)

式中ω为角频率。对每一个角频率分量，在频率域的混合炮数据可用矩阵的形式(图1)表示[1]为

Psim=PΓ

(3)

图1 混合编码过程(每个频率分量)

1.2 混合数据的伪分离

仅从方程的角度看，同时震源数据的分离就是通过式(3)求解原始数据矩阵P，所以形式上可以得到分离结果

(4)

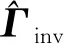
(5)

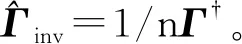
(6)

式(6)表明伪分离法是先复制n份混合数据，再按主炮的延迟时间归位[17]，但仍然保留其他炮的信号，形成串扰噪声。

1.3 构建基础点扩散矩阵

在伪分离中，干扰炮按照主炮的延迟时间处理，而非按照自己的延迟时间归位，形成所谓的“串扰噪声”。不同于常规加约束的迭代反演方法，这里不是简单地将这些干扰炮的“串扰”看成噪声，而是认为这些“串扰噪声”没有得到正确归位。通过讨论同时震源数据的分离与多维反褶积地震干涉技术在原理上的相似性，引入基础点扩散矩阵对混合数据进行处理[25-26]，将“串扰噪声”按各自的延迟时间进行归位。

地震干涉技术可以将任意两个检波器接收到的数据合成为在若干检波器之间传播的波，相当于将其中的一个检波器看作虚拟震源(图2)。

图2 地震干涉的卷积模型

(7)

(8)

(9)

(10)

(11)

式中：Cseq(xB,xA,t)为相关函数；Rseq(x,xA,t)为点扩散函数。其表达式分别为

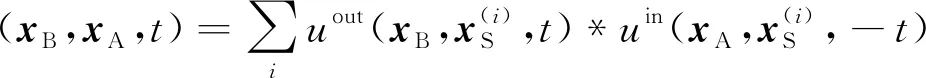
(12)

(13)

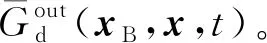
(14)

(15)

在式(9)两边同时与s(i)(t-ti)褶积，并对超级炮σ(m)内的所有单炮求和，得到类似于式(10)的表达式

(16)

对界面T上选取的一个固定参考检波器xA，其记录的波场为uin(xA,σ(m),t)，在式(16)两端同时与uin(xA,σ(m),t)做互相关计算，并对所有超级炮σ(m)求和，则式(11)可以改写为同时震源模型下的相关函数

(17)

式中：Csim(xB,xA,t)代表伪分离后的数据；Rsim(x,xA,t)为点扩散函数。其表达式分别为

uin(xA,σ(m),-t)]

(18)

uin(xA,σ(m),-t)]

(19)

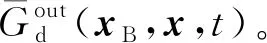
将式(9)变换到频率域，每个频率分量都有如下离散化后的矩阵表达式

(20)

式(14)和式(15)表示同时震源模型中的波场响应，其离散矩阵为

Uin=GinΓ

(21)

Uout=GoutΓ

(22)

在式(20)两端同乘以Γ，得到式(16)的离散矩阵表达式

(23)

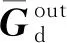
(24)

根据式(19)，Rsim在频率域的矩阵表达式为

Rsim=(Uin)†Uin

(25)

将式(21)代入式(25)，得到

Rsim=Γ†(Gin)†GinΓ=Γ†RΓ

(26)

式中(Gin)†Gin被定义为基础点扩散矩阵(the basic point-spread function)，用符号R表示

R=(Gin)†Gin

(27)

(28)

式中：xi为第i个震源到第1个震源的距离；γ(xi,ω)与二维偏移中的分辨率函数类似[24,27]，与sinc插值函数成正比[25,28]。在信号重建中，重建函数[29]

(29)

表示原始信号g(x)是待重建信号gd(x)与sinc(x)的卷积，由此将sinc(x)离散化。同理将γ(xi,ω)离散化并表示为矩阵R

(30)

式中γi=γ(xi,ω)=γ(iΔs,ω)，Δs为炮间距。

(31)

将式(24)代入上式，并用Gin替代W+[26]，得到

(32)

其中W-Uout为混合后的矩阵Psim，分别将式(21)和式(27)代入上式，得到同时震源的直接反演分离公式

=Psim[(GinΓ)†GinΓ]-1(GinΓ)†Gin

=Psim[Γ†(Gin)†GinΓ]-1Γ†(Gin)†Gin

=Psim(Γ†RΓ)-1Γ†R

(33)

(34)

式中b1=exp(-iωt1),b2=exp(-iωt2)。将式(30)和式(34)代入式Rsim=Γ†RΓ中，得到

(35)

式中Δt=t2-t1。式(35)中右边第一项是式(30)中基础点扩散矩阵R的重采样变形式(采样因子为2)，第二和第三项也是基础点扩散矩阵的重采样变形式，但是对距离的改变量为±Δs，在空间上对串扰噪声进行了归位；因子exp(∓iωΔt)表示时间改变量±Δt，对串扰噪声在时间上进行了归位。式中的第二和第三项解释了对同时震源数据中的串扰噪声的处理方式。在对上式的分析中，假设一个超级炮是由相邻两个单炮混合组成的。如果一个超级炮由n个相邻震源组成，也能够得到类似于式(35)的表达式，只是基础点扩散矩阵R的重采样变形式在空间和时间的改变量会随之发生变化[26]。

直接反演分离的具体流程如图3所示。

1.4 分离适用条件

直接反演分离方法利用地震数据带宽有限的特点，使用与sinc插值函数类似的γ(xi,ω)时，要求直接反演方法满足空间采样定理，不能产生空间假频，这意味着混合度n不能够无限制地增大。

根据远场理论，在共炮域，一个频率为f的平面简谐波入射到地面检波器上，空间假频出现的截止频率为

(36)

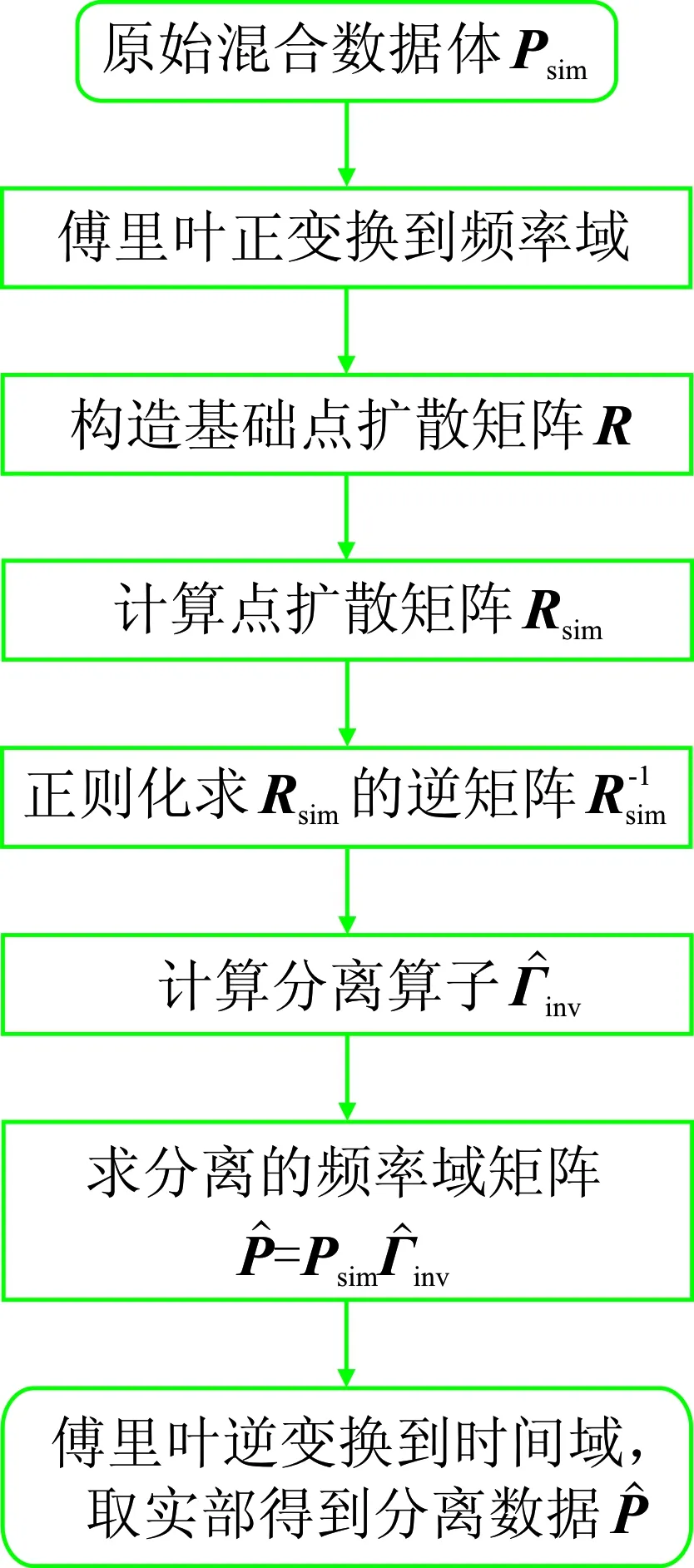
图3 同时震源数据的直接反演分离流程图

式中：v为近地表地震波的传播速度；Δx为检波器间距；θ为地震波的传播角度。根据波场互换原理，把共检波点道集中的检波点视为炮点，炮点视为检波点，则允许截止频率为

(37)

在同时震源数据采集中，相邻n个单炮几乎同时激发，形成一个超级炮，超级炮的间距为

ΔS=nΔs

(38)

由全部超级炮形成的混合波场中，允许的截止频率为

(39)

实际震源激发的频率f应不大于截止频率

(40)

可得

(41)

当满足式(41)时，空间假频就不会出现，才能使用γ(xi,ω)，混合震源才会被正确解混为单个震源。

2 检波点与炮点的不规则排列

在前面原理部分，待分离的同时震源数据体是通过固定炮间距和固定检波点间距的观测系统混合采集得到。在实际生产中，遇到无法避开的障碍物时，不可避免地要改变检波点和炮点间距，形成不规则排列。为了使直接分离算法得到广泛应用，对检波点和炮点都不规则排列的采集条件进行研究。

2.1 检波点不规则排列

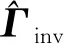
(42)

2.2 炮点不规则排列

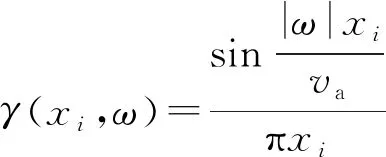
(43)

在炮点不规则排列的观测系统中，防止出现空间假频的分离适用条件(式(41))变为

(44)

式中Δsi为第i炮与第i+1炮之间的距离， Δs1+Δs2+Δs3+…+Δsn代表一个超级炮在地面的覆盖范围。

3 算列

3.1 规则排列下的模拟数据

图4为传播速度具有横向和垂直变化的Marmousi模型。模型的最低速度为1500m/s，正演的震源截止频率为25Hz。在地表创建765个炮点，炮间距为10m，以3个相邻单炮组成一个超级炮，即混合度n=3，因此共有255个超级炮，每个单炮的延迟时间是随机的，取值为0～2s； 用767个检波器接收信号，道间距为10m，采样间隔为4ms。模拟计算在Intel Xeon E7-4807、内存为128G的IBM服务器上运行，使用的编程语言为MATLAB。混合数据体(其中部分道集如图5所示)经过一次处理可以得到全部解混后的数据。

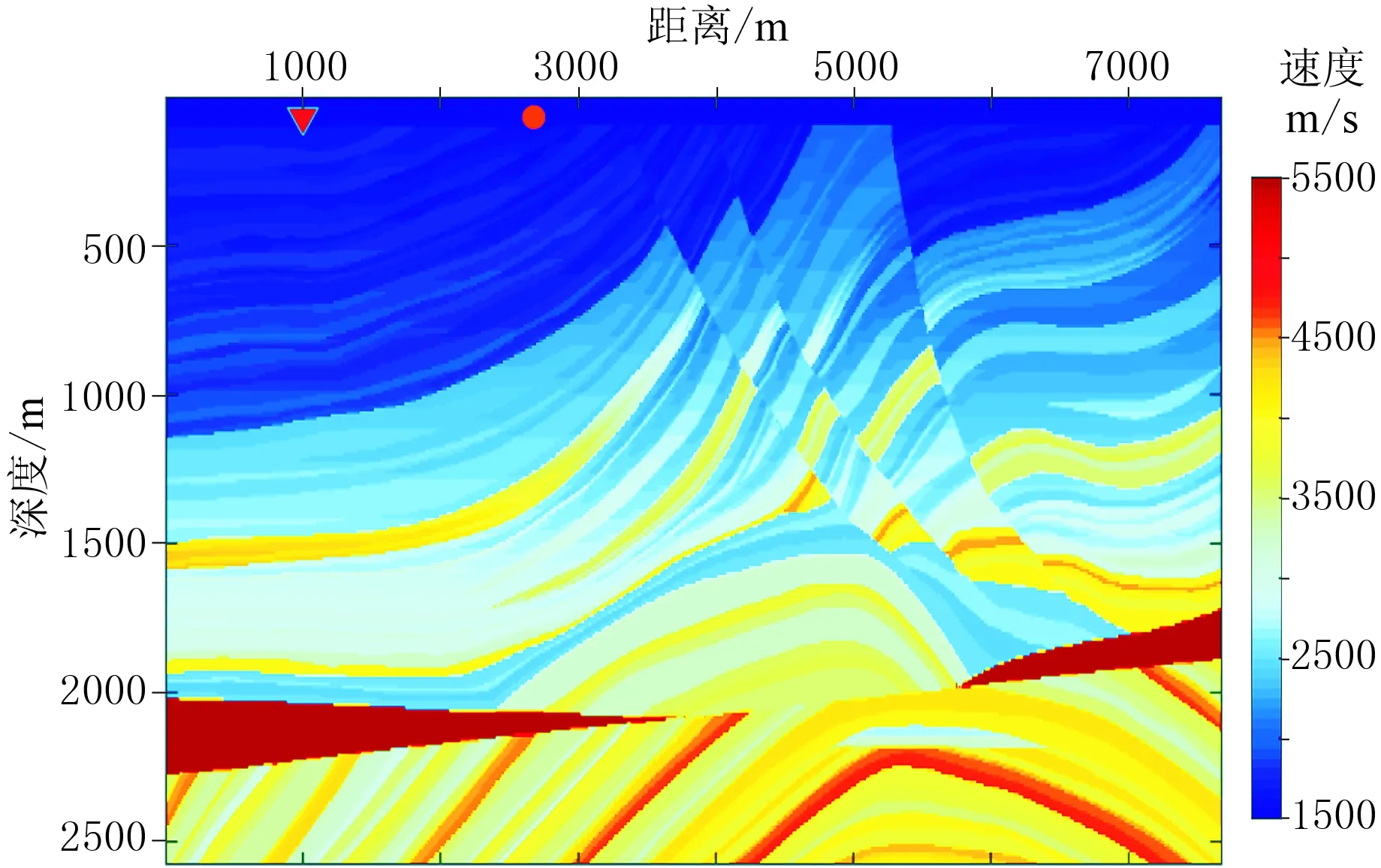
图4 Marmousi速度模型

如果仅采用最小二乘法进行分离，只对主炮进行了归位。图5e为在共检波点道集中用最小二乘法求得的分离结果。对比图5d，可以看出主炮已经归位，但是其他干扰炮形成的“串扰”特征依然存在，这些“串扰”数据携带其他干扰炮的信息，并不能简单地理解为噪声。所以在每个频率分量中，首先构建基础点扩散矩阵R(图6)，然后计算点扩散矩阵Rsim。在共检波点域，矩阵Rsim把这些“串扰”在时间上按各炮的延迟时间进行归位，在空间上按炮间距进行归位，因此混叠的同时震源数据得到了分离。在实际计算中，为了提高矩阵Rsim求逆的稳定性，一般在矩阵Rsim中增加正则化参数β，即Rsim=Γ†RΓ+βI，试验证明β=1.0×10-6ε是一个合理的选择，其中ε是矩阵Rsim中的最大元素。

图5 规则排列下不同时域的原始采集数据与混合采集数据

图6 频率分量12Hz处的基础点扩散矩阵R

根据图3完成后续步骤，得到全部765炮的分离数据。图5中混合采集数据的分离结果见图7。

定义如下信噪比公式定量描述数据分离的效果

(45)

本次实验中，共炮点数据(图5a与图7a)和共检波点数据(图5b与图7b)的分离信噪比SNR分别为37.8dB和35.3dB。抽取第90道和第200道的原始数据(图5b)与分离数据(图7b)进行对比，结果见图8。

在前述的计算机环境下，一次性分离全部混合数据体(由255个超级炮，767个检波点和每道1200个采样点组成)耗时381s，用时较短。对比分离后数据(图7a、图7b)与原始数据(图5a、图5b)，可以看出，不仅浅层数据得到了很好的恢复，深部细节也得到保留，残差较小，信噪比较高，且两条波形曲线的吻合度很高，这证明了本文方法的准确性。

3.2 规则排列下的实际数据

实际数据的炮间距为20m，采样间隔为1ms，观测时间为2.3s，混合度n=2。考虑到截止频率对本方法的影响较大，对实际数据滤波，去掉了高频分量。分离结果及残差见图9c、图9d。可以看出，虽然中间记录道的强“串扰噪声”没能完全被压制，但是分离后的深部反射层的同相轴信号得到了较好的恢复，最终的SNR为10.5dB。

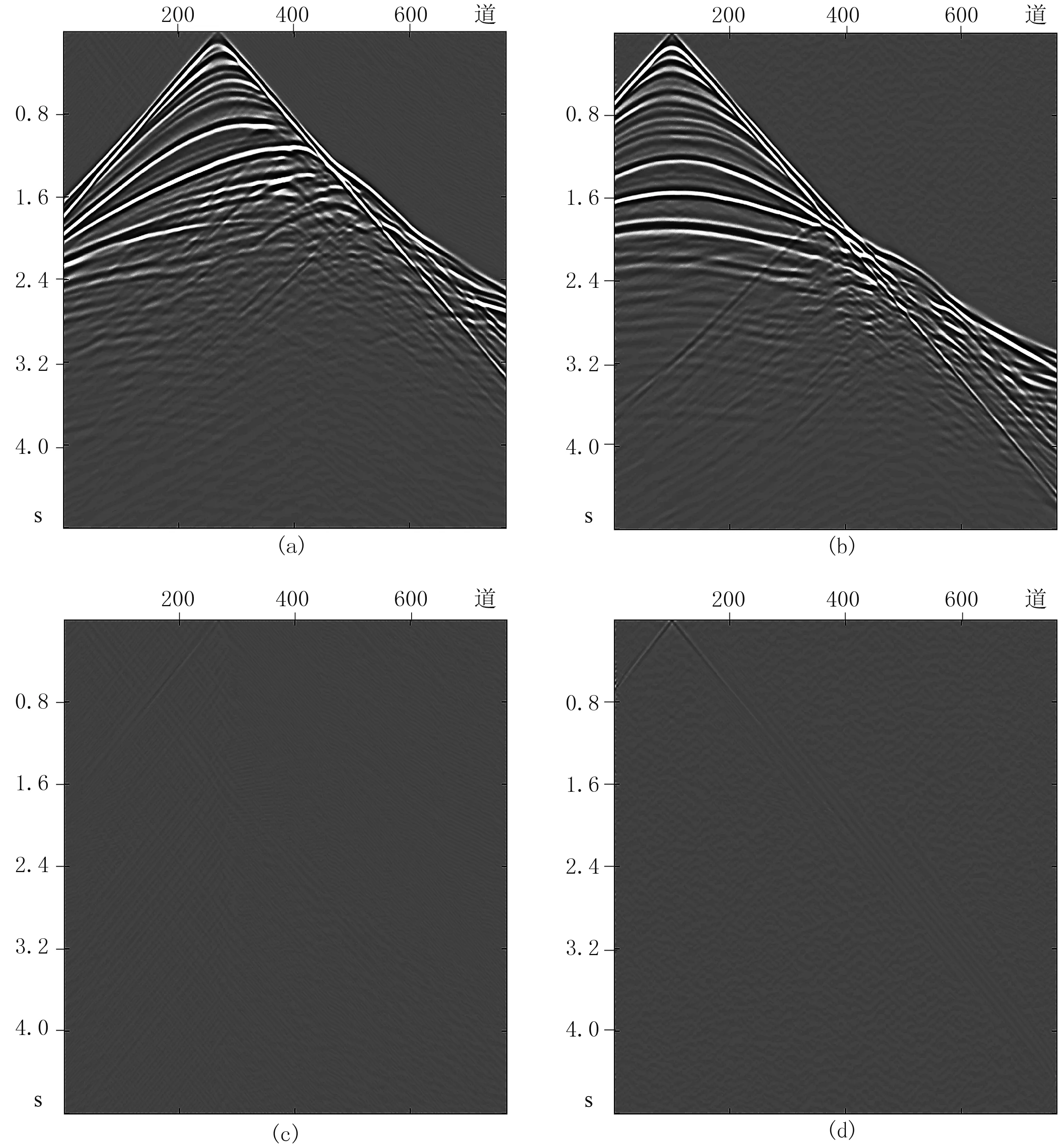
图7 规则排列下不同时域的分离数据与残差

图8 单道分离数据与原始采集数据的波形对比图

3.3 不规则排列的模拟数据

不规则排列的正演速度模型仍为Marmousi模型(图4)。炮点数为765，炮间距随机，但是需要满足分离适用条件(式(44))。检波点数为150，分为3段，每段包含50个检波点，分别布置在地面500～1500m、3000～4000m和5500～6500m，道间距也随机取值。炮点与检波点覆盖范围如图10所示，混合度n=3，其他条件与前述规则排列正演相同。分别讨论当检波点或炮点不规则排列下，同时震源数据的直接反演分离效果。

首先，针对检波点不规则排列得到的同时震源数据进行分离测试(图11)，分离后的信噪比SNR=39.5dB。然后，针对炮点不规则排列的情况进行了测试(图12)，分离的信噪比SNR=38.1dB。对比分离结果(图11c、图12c)与原始采集数据(图11a、图12a)，可以看出，混合波场从浅层到深层都得到了很好的分离，在分离的残差(图11d、图12d)中几乎看不到连续的有效反射信号。证明本文方法不仅适用于规则排列采集的同时震源数据的分离，通过拓展后同样适用于不规则排列采集的同时震源数据的分离。

图9 规则排列下实际共检波点道集数据的直接反演分离

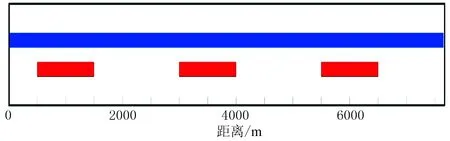
图10 炮点与检波点在地面的覆盖范围示意图

图11 检波点不规则排列条件下共炮点道集数据的直接反演分离

图12 炮点不规则排列下共检波点道集数据的直接反演分离结果

4 讨论

本文在求取矩阵Rsim=Γ†RΓ+βI的逆的过程中采用了正则化方法，该求逆过程会引入较多的假频噪声。通过对正则化参数的研究，选择合适的参数β，可以将这种影响降到最低。图13展示了取不同正则化参数β时，规则排列的Marmousi混合数据体中，第100个检波器记录的共检波点道集的分离信噪比变化曲线。可以看出当参数β取值较大或者较小时，信噪比都会降低，假频噪声增强，分离效果较差； 当β取1.0×10-4ε～1.0×10-8ε时，可以得到较高的信噪比。

算例中，对于检波点与炮点规则排列采集的Marmousi正演混合数据体，分离后可以得到765个共炮点道集和767个共检波点道集，这些共炮点道集与共检波点道集各自的分离信噪比见图14。可以看出，靠近观测系统中部采集的混合数据分离效果较好，处于两端的分离效果相对较差，具体原因还需进一步研究。

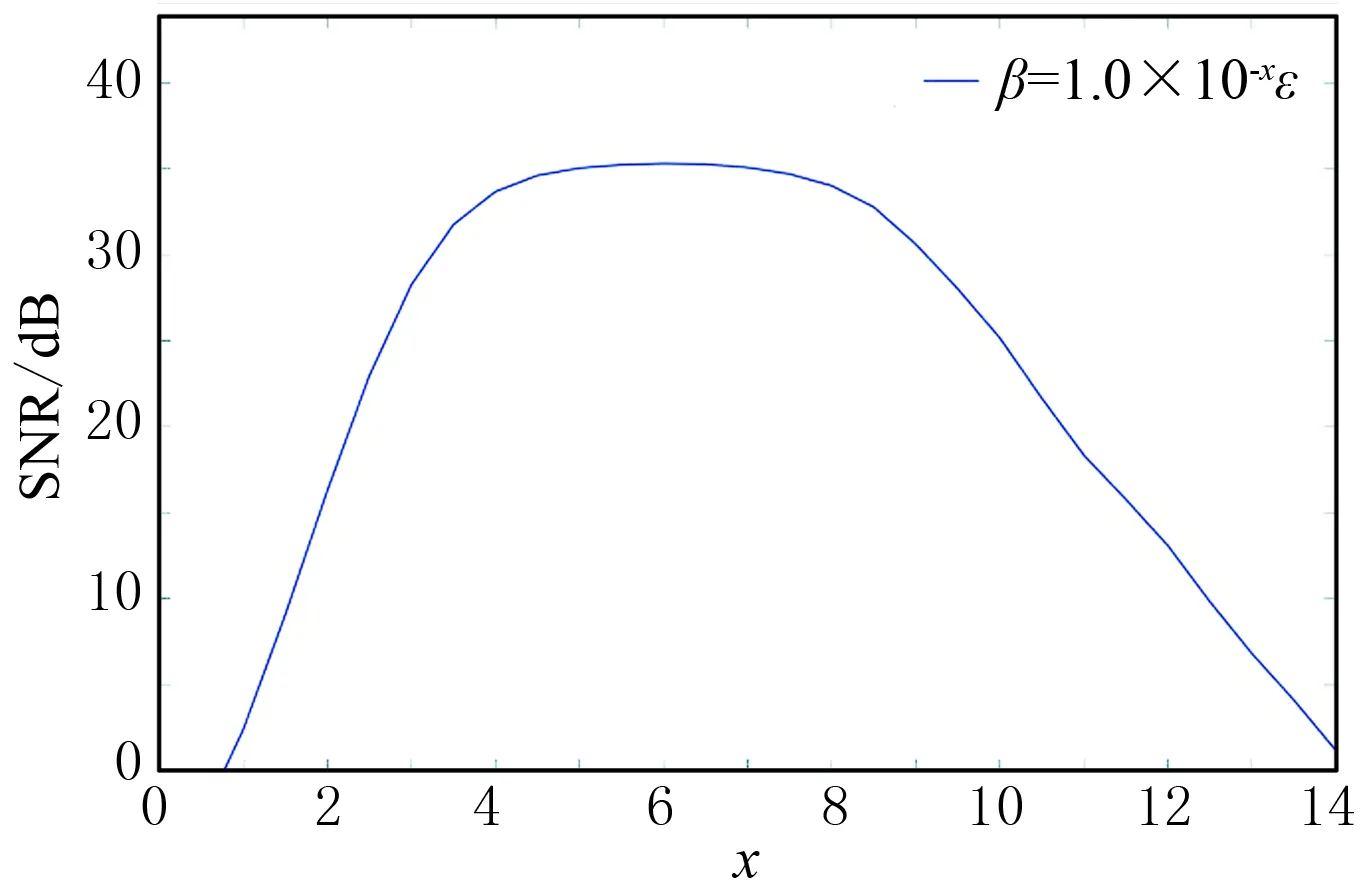
图13 规则排列下的模拟数据算列中正则化参数β对分离SNR的影响

图14 Marmousi模型检波点与炮点规则排列下数据体的全部共炮点道集与共检波点道集分离SNR曲线

5 结论

一般而言，进行高密度震源采样时，若震源间距较小、激发的延迟时间很短，激发波场容易产生强相干性，这不利于同时震源数据的分离。本文采用的直接反演方法则不受这些条件限制，对分离激发延迟时间短、炮间距较小的高密度同时震源数据具有一定的优势。该方法只需在频率域进行一次性分离，不需要迭代，效率高、准确度高，对同时震源数据的分离有很好的应用前景。

通过适当改变基础点扩散矩阵，该方法被推广到检波点和炮点不规则排列的观测系统中，不仅满足陆地复杂地形的同时震源数据的分离，而且适用于海上拖缆的动态不规则采集的混合数据的分离。

需要注意的是，直接反演分离算法有一定的适用范围，要求混合度、炮间距和地震信号的频率满足本文中的分离适用条件。